人教版八年级数学上册12.2 三角形全等的判定(HL)教学设计
文档属性
| 名称 | 人教版八年级数学上册12.2 三角形全等的判定(HL)教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 73.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 00:00:00 | ||
图片预览

文档简介
课题 三角形全等的判定——HL
教学目标
教学目标:1.探索并理解“HL ”判定方法. 2.会用“HL ”判定方法证明两个直角三角形全等. 3.经历猜想、作图、归纳的几何探究过程,发展逻辑推理能力和几何表达能力. 教学重点:理解并运用“HL ”判定方法. 教学难点:“HL ”判定方法的使用条件和注意事项.
教学过程
时 间 教学环节 主要师生活动
3 分 钟 情境引入, 引发思考 问题:如图,舞台背景的形状是两个直角三角形, 为了美观, 工作人员想知道这两个直角三角形是否全等,但每个三角形都 有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法 吗? (1)如果用直尺和量角器两种工具,你能解决这个问题吗? (测量其中的一边和一角) (2)如果只用直尺,你能解决这个问题吗? (测量未被遮挡的两边) 思考:斜边和一条直角边分别相等的两直角三角形全等吗?
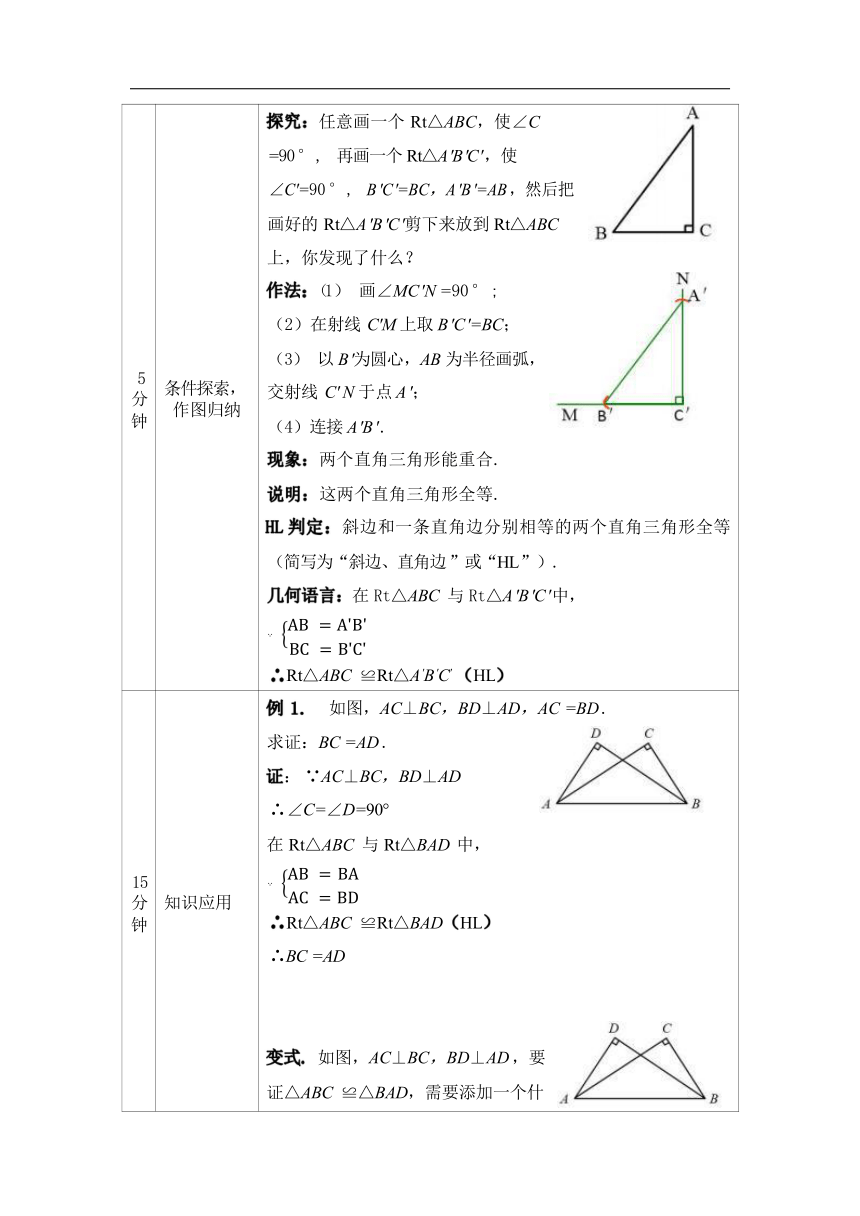
5 分 钟 条件探索, 作图归纳 探究:任意画一个 Rt△ABC,使∠C =90 ° , 再画一个 Rt△A ′B ′C ′ ,使 ∠C′=90 ° , B ′C ′=BC,A ′B ′=AB ,然后把 画好的 Rt△A ′B ′C ′剪下来放到 Rt△ABC 上,你发现了什么? 作法:(1) 画∠MC ′N =90 ° ; (2)在射线 C′M 上取 B ′C ′=BC; (3) 以 B ′为圆心,AB 为半径画弧, 交射线 C′ N 于点 A ′; (4)连接 A ′B ′ . 现象:两个直角三角形能重合. 说明:这两个直角三角形全等. HL 判定:斜边和一条直角边分别相等的两个直角三角形全等 (简写为“斜边、直角边 ”或“HL ”). 几何语言:在 Rt△ABC 与 Rt△A ′B ′C ′ 中, (
∵
) (
BC
=
B'C'
)AB = A'B' ∴Rt△ABC ≌Rt△A ′B ′C′ (HL)
15 分 钟 知识应用 例 1. 如图,AC⊥BC,BD⊥AD,AC =BD . 求证:BC =AD . 证: ∵AC⊥BC,BD⊥AD ∴∠C=∠D=90° 在 Rt△ABC 与 Rt△BAD 中, (
∵
) (
AC
=
BD
)AB = BA ∴Rt△ABC ≌Rt△BAD(HL) ∴BC =AD
变式. 如图,AC⊥BC,BD⊥AD ,要 证△ABC ≌△BAD,需要添加一个什
么条件?请说明理由. (1)AD = BC 理由:HL (2)AC = BD 理由:HL (3) ∠DBA = ∠CAB 理由:AAS (4) ∠DAB = ∠CBA 理由:AAS 例 2. 如图,C 是路段 AB 的中点, 两人从 C 同时出发,以相同的速度分 别沿两条直线行走,并同时到达 D,E 两地.DA⊥AB ,EB⊥AB . D ,E 与 路段 AB 的距离相等吗?为什么? 解:D,E 与路段 AB 的距离相等. 理由: ∵C 是路段 AB 的中点, ∴AC=BC 又∵DA⊥AB,EB⊥AB ∴∠A=∠B=90 ° 在 Rt△ACD 与 Rt△BCE 中, (
∵
) (
AC
=
BC
){DC = EC ∴Rt△ACD ≌Rt△BCE(HL) ∴DA =EB(全等三角形的对应边相等)
例 3.如图,AB =CD,AE⊥BC,DF⊥BC, 垂足分别为 E ,F,CE =BF. 求证:(1)AE =DF (2)CD//AB 证: ∵CE=BF ∴CE-EF=BF-EF,即 CF=BE ∵AE⊥BC,DF⊥BC ∴∠DFC=∠AEB=90° 在 Rt△AEB 与 Rt△DFC 中, (
∵
) (
BE
=
CF
){AB = DC ∴Rt△AEB ≌Rt△DFC(HL)
∴AE=DF,∠C=∠B ∴CD//AB 例 4.如图,已知 AB=AC,AE=AF, AE⊥EC,AF⊥BF,垂足分别是点 E、 F.求证: ∠1=∠2. 证: ∵AE⊥EC,AF⊥BF, ∴∠E=∠F=90° 在 Rt△AEC 与 Rt△AFB 中, (
∵
) (
=
) = ∴Rt△AEC ≌Rt△AFB(HL) ∴∠EAC=∠FAB
∴∠EAC- ∠BAC=∠FAB- ∠BAC,即∠1=∠2 .
变式. 在例 4 的基础上,设 EC 与 AB 交于点 M,BF 与 AC 交于点 N,那么 EM 和 FN 相等吗?请说明理由. 解:EM=FN 理由:在 Rt△AEM 与 Rt△AFN 中 (
∠1
=
∠2
) (
∠
=
∠
=
90°
) = ∵ ∴Rt△AEM ≌Rt△AFN(ASA) ∴EM=FN
2 分 钟 课堂小结 1.“HL ”判定方法应满足什么条件?与之前所学的四种判定 方法有什么不同? 斜边和一条直角边分别相等的两个直角三角形全等. ①此判定方法只针对两个直角三角形,而之前所学的判定适用 于任意三角形.
②此判定方法在直角三角形的前提下,只需满足两条边(斜边 与一直角边)相等即可;之前的判定方法都需满足三个条件. 2.判定两个直角三角形全等有哪些方法? SSS ,SAS ,ASA ,AAS ,HL 注意:由于已有直角条件,所以我们多使用后 4 个判定方法.
课后作业 1. 如图,在△ABC 中,AB=AC,AD 是高. 求证:(1)BD=CD;(2) ∠BAD=∠CAD A
(
D
C
B
)
2. 用三角板可按下面方法画角平分线:在已知∠AOB 的两边 上,分别取 OM=ON(如图),再分别过点 M、N 作 OA、 OB 的垂线,交点为 P,画射线 OP,则 OP 平分∠AOB,请 你说出其中的道理.
教学目标
教学目标:1.探索并理解“HL ”判定方法. 2.会用“HL ”判定方法证明两个直角三角形全等. 3.经历猜想、作图、归纳的几何探究过程,发展逻辑推理能力和几何表达能力. 教学重点:理解并运用“HL ”判定方法. 教学难点:“HL ”判定方法的使用条件和注意事项.
教学过程
时 间 教学环节 主要师生活动
3 分 钟 情境引入, 引发思考 问题:如图,舞台背景的形状是两个直角三角形, 为了美观, 工作人员想知道这两个直角三角形是否全等,但每个三角形都 有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法 吗? (1)如果用直尺和量角器两种工具,你能解决这个问题吗? (测量其中的一边和一角) (2)如果只用直尺,你能解决这个问题吗? (测量未被遮挡的两边) 思考:斜边和一条直角边分别相等的两直角三角形全等吗?
5 分 钟 条件探索, 作图归纳 探究:任意画一个 Rt△ABC,使∠C =90 ° , 再画一个 Rt△A ′B ′C ′ ,使 ∠C′=90 ° , B ′C ′=BC,A ′B ′=AB ,然后把 画好的 Rt△A ′B ′C ′剪下来放到 Rt△ABC 上,你发现了什么? 作法:(1) 画∠MC ′N =90 ° ; (2)在射线 C′M 上取 B ′C ′=BC; (3) 以 B ′为圆心,AB 为半径画弧, 交射线 C′ N 于点 A ′; (4)连接 A ′B ′ . 现象:两个直角三角形能重合. 说明:这两个直角三角形全等. HL 判定:斜边和一条直角边分别相等的两个直角三角形全等 (简写为“斜边、直角边 ”或“HL ”). 几何语言:在 Rt△ABC 与 Rt△A ′B ′C ′ 中, (
∵
) (
BC
=
B'C'
)AB = A'B' ∴Rt△ABC ≌Rt△A ′B ′C′ (HL)
15 分 钟 知识应用 例 1. 如图,AC⊥BC,BD⊥AD,AC =BD . 求证:BC =AD . 证: ∵AC⊥BC,BD⊥AD ∴∠C=∠D=90° 在 Rt△ABC 与 Rt△BAD 中, (
∵
) (
AC
=
BD
)AB = BA ∴Rt△ABC ≌Rt△BAD(HL) ∴BC =AD
变式. 如图,AC⊥BC,BD⊥AD ,要 证△ABC ≌△BAD,需要添加一个什
么条件?请说明理由. (1)AD = BC 理由:HL (2)AC = BD 理由:HL (3) ∠DBA = ∠CAB 理由:AAS (4) ∠DAB = ∠CBA 理由:AAS 例 2. 如图,C 是路段 AB 的中点, 两人从 C 同时出发,以相同的速度分 别沿两条直线行走,并同时到达 D,E 两地.DA⊥AB ,EB⊥AB . D ,E 与 路段 AB 的距离相等吗?为什么? 解:D,E 与路段 AB 的距离相等. 理由: ∵C 是路段 AB 的中点, ∴AC=BC 又∵DA⊥AB,EB⊥AB ∴∠A=∠B=90 ° 在 Rt△ACD 与 Rt△BCE 中, (
∵
) (
AC
=
BC
){DC = EC ∴Rt△ACD ≌Rt△BCE(HL) ∴DA =EB(全等三角形的对应边相等)
例 3.如图,AB =CD,AE⊥BC,DF⊥BC, 垂足分别为 E ,F,CE =BF. 求证:(1)AE =DF (2)CD//AB 证: ∵CE=BF ∴CE-EF=BF-EF,即 CF=BE ∵AE⊥BC,DF⊥BC ∴∠DFC=∠AEB=90° 在 Rt△AEB 与 Rt△DFC 中, (
∵
) (
BE
=
CF
){AB = DC ∴Rt△AEB ≌Rt△DFC(HL)
∴AE=DF,∠C=∠B ∴CD//AB 例 4.如图,已知 AB=AC,AE=AF, AE⊥EC,AF⊥BF,垂足分别是点 E、 F.求证: ∠1=∠2. 证: ∵AE⊥EC,AF⊥BF, ∴∠E=∠F=90° 在 Rt△AEC 与 Rt△AFB 中, (
∵
) (
=
) = ∴Rt△AEC ≌Rt△AFB(HL) ∴∠EAC=∠FAB
∴∠EAC- ∠BAC=∠FAB- ∠BAC,即∠1=∠2 .
变式. 在例 4 的基础上,设 EC 与 AB 交于点 M,BF 与 AC 交于点 N,那么 EM 和 FN 相等吗?请说明理由. 解:EM=FN 理由:在 Rt△AEM 与 Rt△AFN 中 (
∠1
=
∠2
) (
∠
=
∠
=
90°
) = ∵ ∴Rt△AEM ≌Rt△AFN(ASA) ∴EM=FN
2 分 钟 课堂小结 1.“HL ”判定方法应满足什么条件?与之前所学的四种判定 方法有什么不同? 斜边和一条直角边分别相等的两个直角三角形全等. ①此判定方法只针对两个直角三角形,而之前所学的判定适用 于任意三角形.
②此判定方法在直角三角形的前提下,只需满足两条边(斜边 与一直角边)相等即可;之前的判定方法都需满足三个条件. 2.判定两个直角三角形全等有哪些方法? SSS ,SAS ,ASA ,AAS ,HL 注意:由于已有直角条件,所以我们多使用后 4 个判定方法.
课后作业 1. 如图,在△ABC 中,AB=AC,AD 是高. 求证:(1)BD=CD;(2) ∠BAD=∠CAD A
(
D
C
B
)
2. 用三角板可按下面方法画角平分线:在已知∠AOB 的两边 上,分别取 OM=ON(如图),再分别过点 M、N 作 OA、 OB 的垂线,交点为 P,画射线 OP,则 OP 平分∠AOB,请 你说出其中的道理.
