3.2角-四年级数学上册课后作业(含解析)人教版
文档属性
| 名称 | 3.2角-四年级数学上册课后作业(含解析)人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 227.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-17 05:03:14 | ||
图片预览


文档简介
3.2 角(同步练习)
一、填空题
1 .角的大小与角的两边( )没有关系,要看两条边( )的大小。
2 .120°的角比平角小( ),比直角大( )。
3 .从一点引出两条( )线所组成的图形叫做角,这个点叫做角的( ),
这两条射线叫做角的( ),如果将这两条线延长,角的大小( )。
4 .下图中各有几个角?数一数。
( )个角 ( )个角
二、判断题
5 .10°的角在放大 10 倍的放大镜下看是 100°的角.( )
6 .把一个 80°的角放在放大 10 倍的放大镜下面,看到的角还是 80° . ( )
7 .角的大小与它两条边的张开程度有关,也与两条边的长度有关。 ( )
三、选择题
8 .角的两条边是两条( )。
A .射线 B .线段 C .直线
9 .图中共有( )个角。
A .8 B .10 C .12
10 .判断下面的图形, 是角( )
A . B . C .
11 .用一个放大 100 倍的放大镜看一个 45°的角,看到的角的度数是( )。
A .450° B .45° C .4500°
四、解答题
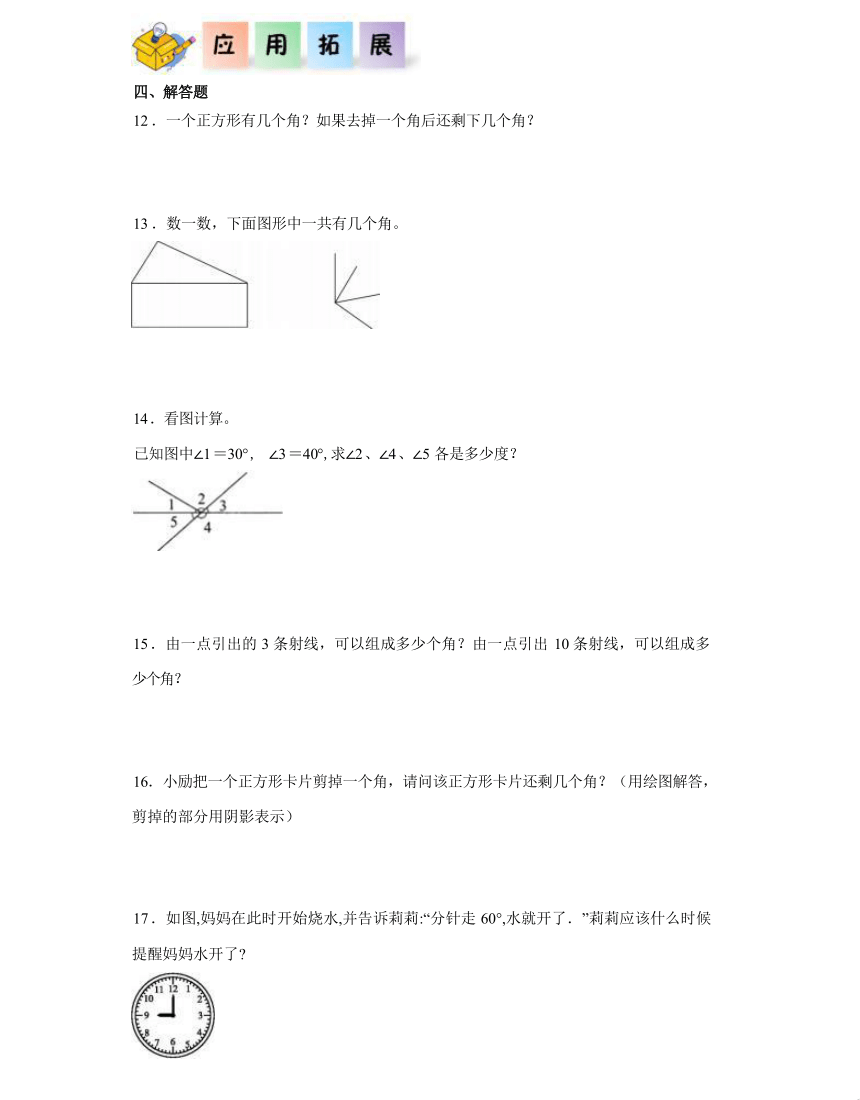
12 .一个正方形有几个角?如果去掉一个角后还剩下几个角?
13 .数一数,下面图形中一共有几个角。
14 .看图计算。
已知图中∠1 =30° , ∠3 =40°,求∠2 、∠4 、∠5 各是多少度?
15 .由一点引出的 3 条射线,可以组成多少个角?由一点引出 10 条射线,可以组成多
少个角?
16.小励把一个正方形卡片剪掉一个角,请问该正方形卡片还剩几个角?(用绘图解答,
剪掉的部分用阴影表示)
17 .如图,妈妈在此时开始烧水,并告诉莉莉:“分针走 60°,水就开了.”莉莉应该什么时候
提醒妈妈水开了
18 .下列图形中,有多少个小于 180。的角?
1 . 长短 叉开
【详解】角的大小与角的两边长短没有关系,要看两条边叉开的大小。
2 . 60° 30°
【分析】平角是 180°,直角是 90°。要求 120°的角比平角小多少,用 180°减去 120°解答。
要求 120°的角比直角大多少,用 120°减去 90°解答。
【详解】 180°-120° =60°
120°-90° =30°
120°的角比平角小 60°,比直角大 30°。
【点睛】本题关键是明确平角和直角的度数,再进一步解答。
3 . 射 顶点 边 不变
【详解】根据角的定义和角特点可知:从一点引出两条射线所组成的图形叫做角,这个点叫 做角的顶点, 这两条射线叫做角的边, 角的两条边是射线, 可以向一端无限延伸, 所以角的
大小和边的长短没有关系,如果将这两条线延长,角的大小不变。
4 . 6 8
【分析】先数一个一个的角,再数两个组合的角,最后数 3 个组合的角,据此数数解答。
【详解】
【点睛】本题考查了角的数数方法,在数角时要按一定的顺序数,不要漏数。
5 . ×
6 . √
7 . ×
【详解】角的大小与它两条边的张开程度有关,与两条边的长度无关。
例如:
∠ 1 和∠2 张开程度不同,大小不同;
∠3 和∠4 两条边的长度不同,大小相等。
故答案为: ×
8 .A
【分析】从一点引出两条射线所组成的图形叫做角,依此选择。
【详解】根据分析可知,角的两条边是两条射线(如图所示)。
故答案为: A
【点睛】熟练掌握角的特点是解答此题的关键。
9 .B
【分析】图中单独的角有 4 个, 由两个单独的角组成的角有 3 个, 由三个单独的角组成的角
有 2 个,由四个单独的角组成的角有 1 个,则一共有 4+3+2+1 =10 个角。
【详解】4+3+2+1 =10(个)
则图中共有 10 个角。
故答案为: B。
【点睛】从一点引出两条射线所形成的图形叫做角。数角的个数时, 要按照顺序数, 才能做
到不重不漏。
10 .A
11 .B
【分析】因为角的大小和边长无关,更和放大无关,只和两条边张开的度数有关。
【详解】用一个放大 100 倍的放大镜看一个 45°的角,看到的角的度数仍然是 45°。
故答案为: B
【点睛】此题主要考查角的定义。
12 .4 个;可能是 5 个角;或者 4 个角;或者 3 个角
【分析】根据正方形的特征,正方形有 4 个角,都是直角;题中说的去掉一个角,但没有规
定怎么剪。
(1)若剪掉正方形相邻两条边的一部分,则剩下的部分是五边形,有 5 个角;
(2)若从正方形一个角的顶点,沿直线向对角的邻边剪,且只剪掉一条邻边的一部分,则
剩下的部分为四边形,有 4 个角;
(3)若沿着正方形的对角线剪,则剩余部分为三角形,有 3 个角;据此解答即可。
【详解】一个正方形有 4 个角。
如图有 3 种剪法:
如果去掉一个角后还剩下的角可能是 5 个角;或者 4 个角;或者 3 个角。
【点睛】本题要结合实际,通过画图可以得出结论,要注意考虑到各种情况。
13 .图一:9 个
图二: 6 个
【分析】第一个图形三角形有 3 个角,长方形有 4 个角,长方形和三角形相接处有 2 个角, 共 9 个角;图 2 小角 3 个,大角 1 个,两个小角组成的一个角,有 2 个,共 6 个角;据此即
可解答。
【详解】图一:3+4+2
=7+2
=9(个)
图二: 3+2+1
=5+1
=6(个)
【点睛】熟练掌握角的概念是解答此题的关键。
14 . ∠2 =110° ∠5 =40° ∠4 =140°
【分析】由,∠ 1 、∠2 和∠3 的和是 180° , ∠2 、∠ 1 和∠5 的和是 180° , ∠4 和∠5 的和是 180° , 由此顺次解答即可。此题利用平角是 180°, 直角 90°这些固定不变的条件, 结合具体的图形
来解答即可。
【详解】如图
∠2 =180° -∠ 1 -∠3 =180° -30° -40° = 110° ,
∠5 =180° -∠ 1 -∠2 =180° -30° -110° =40° ,
∠4 =180° -∠5 =180° -40° = 140°
15 .3 个; 45 个
【分析】从一点出发引出 3 条射线, 每一条射线都分别与其它的射线组成一个角, 所以 3 条
射线就可以组成 2+1 =3 个角;
从一点出发引出 10 条射线,每一条射线都分别与其它的射线组成一个角,依此可得组成角
的个数是 9+8+7+6+5+4+3+2+1 =45 个角。
【详解】2+1 =3(个)
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
= 10×9÷2
=90÷2
=45(个)
答:由一点引出的 3 条射线,可以组成 3 个角;由一点引出 10 条射线,可以组成 45 个角。
【点睛】本题考查了数角的概念,要有总结规律的能力或公式应用的能力。
16 .3 个角, 4 个角或 5 个角
【分析】减掉一个角, 减去的部分是直角三角形, 可能是正方形的一半, 也可能一条边等于
正方形边长,也可能两条边都不等于边长。
【详解】如图所示:
减掉一个角,剩下的图形可能是三角形,四边形,五边形,所以可能有 3 个角、 4 个角、 5
个角;
答:还剩 3 个角, 4 个角或 5 个角。
【点睛】本题考查的是图形的剪切,注意要考虑到所有的情况,然后进行分类讨论。
17 .9 时 10 分
18 .(1)10 个;(2)15 个
【分析】第(1)问,可以先数单独的角,再数两两组合的角,再数三个组合起来的角,依
此类推;第(2)问,分别数出每一个点处的角的数量,相加得到总数。
【详解】(1)这个图中含有四个基本角① 、② 、③ 、④, 如下图所示, 下面我们对角进行
分类:
只含一个基本角的角有 4 个,即① 、② 、③ 、④;
含两个基本角的角有 3 个,即①② 、②③ 、③④;
含三个基本角的角有 2 个,即①②③ 、②③④;
含四个基本角的角有 1 个,即①②③④;
综上,上述图形中一共有角4 + 3 + 2 +1 = 10 (个)。
(2)我们把这个图形中的角分成 6 个区域来数,如下图所示的 6 个区域:
① 、②两图各有角1+ 2 = 3 (个);
③ 、④两图中各有角 2 个;
⑤中有角 4 个; ⑥中有角 1 个;
综上,上述图中有角3 2 + 2 2 + 4 +1 = 15 (个);
答:图(1)有 10 个角,图(2)有 15 个角。
【点睛】本题考查的是几何计数问题,其中图(1)中数角的方法与数线段的方法类似。
一、填空题
1 .角的大小与角的两边( )没有关系,要看两条边( )的大小。
2 .120°的角比平角小( ),比直角大( )。
3 .从一点引出两条( )线所组成的图形叫做角,这个点叫做角的( ),
这两条射线叫做角的( ),如果将这两条线延长,角的大小( )。
4 .下图中各有几个角?数一数。
( )个角 ( )个角
二、判断题
5 .10°的角在放大 10 倍的放大镜下看是 100°的角.( )
6 .把一个 80°的角放在放大 10 倍的放大镜下面,看到的角还是 80° . ( )
7 .角的大小与它两条边的张开程度有关,也与两条边的长度有关。 ( )
三、选择题
8 .角的两条边是两条( )。
A .射线 B .线段 C .直线
9 .图中共有( )个角。
A .8 B .10 C .12
10 .判断下面的图形, 是角( )
A . B . C .
11 .用一个放大 100 倍的放大镜看一个 45°的角,看到的角的度数是( )。
A .450° B .45° C .4500°
四、解答题
12 .一个正方形有几个角?如果去掉一个角后还剩下几个角?
13 .数一数,下面图形中一共有几个角。
14 .看图计算。
已知图中∠1 =30° , ∠3 =40°,求∠2 、∠4 、∠5 各是多少度?
15 .由一点引出的 3 条射线,可以组成多少个角?由一点引出 10 条射线,可以组成多
少个角?
16.小励把一个正方形卡片剪掉一个角,请问该正方形卡片还剩几个角?(用绘图解答,
剪掉的部分用阴影表示)
17 .如图,妈妈在此时开始烧水,并告诉莉莉:“分针走 60°,水就开了.”莉莉应该什么时候
提醒妈妈水开了
18 .下列图形中,有多少个小于 180。的角?
1 . 长短 叉开
【详解】角的大小与角的两边长短没有关系,要看两条边叉开的大小。
2 . 60° 30°
【分析】平角是 180°,直角是 90°。要求 120°的角比平角小多少,用 180°减去 120°解答。
要求 120°的角比直角大多少,用 120°减去 90°解答。
【详解】 180°-120° =60°
120°-90° =30°
120°的角比平角小 60°,比直角大 30°。
【点睛】本题关键是明确平角和直角的度数,再进一步解答。
3 . 射 顶点 边 不变
【详解】根据角的定义和角特点可知:从一点引出两条射线所组成的图形叫做角,这个点叫 做角的顶点, 这两条射线叫做角的边, 角的两条边是射线, 可以向一端无限延伸, 所以角的
大小和边的长短没有关系,如果将这两条线延长,角的大小不变。
4 . 6 8
【分析】先数一个一个的角,再数两个组合的角,最后数 3 个组合的角,据此数数解答。
【详解】
【点睛】本题考查了角的数数方法,在数角时要按一定的顺序数,不要漏数。
5 . ×
6 . √
7 . ×
【详解】角的大小与它两条边的张开程度有关,与两条边的长度无关。
例如:
∠ 1 和∠2 张开程度不同,大小不同;
∠3 和∠4 两条边的长度不同,大小相等。
故答案为: ×
8 .A
【分析】从一点引出两条射线所组成的图形叫做角,依此选择。
【详解】根据分析可知,角的两条边是两条射线(如图所示)。
故答案为: A
【点睛】熟练掌握角的特点是解答此题的关键。
9 .B
【分析】图中单独的角有 4 个, 由两个单独的角组成的角有 3 个, 由三个单独的角组成的角
有 2 个,由四个单独的角组成的角有 1 个,则一共有 4+3+2+1 =10 个角。
【详解】4+3+2+1 =10(个)
则图中共有 10 个角。
故答案为: B。
【点睛】从一点引出两条射线所形成的图形叫做角。数角的个数时, 要按照顺序数, 才能做
到不重不漏。
10 .A
11 .B
【分析】因为角的大小和边长无关,更和放大无关,只和两条边张开的度数有关。
【详解】用一个放大 100 倍的放大镜看一个 45°的角,看到的角的度数仍然是 45°。
故答案为: B
【点睛】此题主要考查角的定义。
12 .4 个;可能是 5 个角;或者 4 个角;或者 3 个角
【分析】根据正方形的特征,正方形有 4 个角,都是直角;题中说的去掉一个角,但没有规
定怎么剪。
(1)若剪掉正方形相邻两条边的一部分,则剩下的部分是五边形,有 5 个角;
(2)若从正方形一个角的顶点,沿直线向对角的邻边剪,且只剪掉一条邻边的一部分,则
剩下的部分为四边形,有 4 个角;
(3)若沿着正方形的对角线剪,则剩余部分为三角形,有 3 个角;据此解答即可。
【详解】一个正方形有 4 个角。
如图有 3 种剪法:
如果去掉一个角后还剩下的角可能是 5 个角;或者 4 个角;或者 3 个角。
【点睛】本题要结合实际,通过画图可以得出结论,要注意考虑到各种情况。
13 .图一:9 个
图二: 6 个
【分析】第一个图形三角形有 3 个角,长方形有 4 个角,长方形和三角形相接处有 2 个角, 共 9 个角;图 2 小角 3 个,大角 1 个,两个小角组成的一个角,有 2 个,共 6 个角;据此即
可解答。
【详解】图一:3+4+2
=7+2
=9(个)
图二: 3+2+1
=5+1
=6(个)
【点睛】熟练掌握角的概念是解答此题的关键。
14 . ∠2 =110° ∠5 =40° ∠4 =140°
【分析】由,∠ 1 、∠2 和∠3 的和是 180° , ∠2 、∠ 1 和∠5 的和是 180° , ∠4 和∠5 的和是 180° , 由此顺次解答即可。此题利用平角是 180°, 直角 90°这些固定不变的条件, 结合具体的图形
来解答即可。
【详解】如图
∠2 =180° -∠ 1 -∠3 =180° -30° -40° = 110° ,
∠5 =180° -∠ 1 -∠2 =180° -30° -110° =40° ,
∠4 =180° -∠5 =180° -40° = 140°
15 .3 个; 45 个
【分析】从一点出发引出 3 条射线, 每一条射线都分别与其它的射线组成一个角, 所以 3 条
射线就可以组成 2+1 =3 个角;
从一点出发引出 10 条射线,每一条射线都分别与其它的射线组成一个角,依此可得组成角
的个数是 9+8+7+6+5+4+3+2+1 =45 个角。
【详解】2+1 =3(个)
9+8+7+6+5+4+3+2+1
=(9+1)×9÷2
= 10×9÷2
=90÷2
=45(个)
答:由一点引出的 3 条射线,可以组成 3 个角;由一点引出 10 条射线,可以组成 45 个角。
【点睛】本题考查了数角的概念,要有总结规律的能力或公式应用的能力。
16 .3 个角, 4 个角或 5 个角
【分析】减掉一个角, 减去的部分是直角三角形, 可能是正方形的一半, 也可能一条边等于
正方形边长,也可能两条边都不等于边长。
【详解】如图所示:
减掉一个角,剩下的图形可能是三角形,四边形,五边形,所以可能有 3 个角、 4 个角、 5
个角;
答:还剩 3 个角, 4 个角或 5 个角。
【点睛】本题考查的是图形的剪切,注意要考虑到所有的情况,然后进行分类讨论。
17 .9 时 10 分
18 .(1)10 个;(2)15 个
【分析】第(1)问,可以先数单独的角,再数两两组合的角,再数三个组合起来的角,依
此类推;第(2)问,分别数出每一个点处的角的数量,相加得到总数。
【详解】(1)这个图中含有四个基本角① 、② 、③ 、④, 如下图所示, 下面我们对角进行
分类:
只含一个基本角的角有 4 个,即① 、② 、③ 、④;
含两个基本角的角有 3 个,即①② 、②③ 、③④;
含三个基本角的角有 2 个,即①②③ 、②③④;
含四个基本角的角有 1 个,即①②③④;
综上,上述图形中一共有角4 + 3 + 2 +1 = 10 (个)。
(2)我们把这个图形中的角分成 6 个区域来数,如下图所示的 6 个区域:
① 、②两图各有角1+ 2 = 3 (个);
③ 、④两图中各有角 2 个;
⑤中有角 4 个; ⑥中有角 1 个;
综上,上述图中有角3 2 + 2 2 + 4 +1 = 15 (个);
答:图(1)有 10 个角,图(2)有 15 个角。
【点睛】本题考查的是几何计数问题,其中图(1)中数角的方法与数线段的方法类似。
