2.3二次函数与一元二次方程、不等式(第一课时)教学设计(表格式)
文档属性
| 名称 | 2.3二次函数与一元二次方程、不等式(第一课时)教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 215.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 23:26:59 | ||
图片预览

文档简介
课题 二次函数与一元二次方程、不等式(1)
教学目标
教学目标: 1. 经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义; 2. 理解一元二次不等式与相应函数、方程的联系,认识到函数的重要性,体会数学的整体性; 3. 能够体会归纳,概括的方法,把握三者之间的内在联系,借助二次函数,求解一元二次不等式,渗 透数学建模的素养,提升数学运算素养. 教学重点: 从函数的观点看一元二次方程、一元二次不等式,在建立二次函数与一元二次方程、不等式的联系中, 获得用二次函数求解一元二次不等式的一般性方法. 教学难点: 从函数的观点看一元二次方程、一元二次不等式,并归纳概括出一元二次不等式的一般性解法.
教学过程
时间 教学环节 主要师生活动
5 引入 同学们,大家好,今天我们来一起学习第二章第三节,二次函数与一元二次 方程、不等式. 二次函数与一元二次方程我们已在初中学过,你还记得它们吗? 我们先来复习二次函数 = 2 + + ≠ 0的图象及性质: 这条 条轴抛是物否线交开以口及向交上点或可者以向由下判) 2 轴4对, 当 > 0 时,这条抛物线与 轴有两个不同的交点; 当 = 0 时,这条抛物线与 轴有且仅有一个交点; 当 < 0 时,这条抛物线与 轴无交点; 那么我们如何求解交点的横坐标呢? 借助一元二次方程: 2 + + = 0 ≠ 0 当1 => 0 22 4二,次2 方=程 有两个不相 22 4 等的实根 当 = 0 时,一元二次方程有两个相等的实根:1 = 2 = 当 < 0 时,方程无实根. 下面我给出一个新的定义,二次函数的零点. 二次函数的零点:一般地,对于二次函数 = 2 + + ,我们把使2 + + = 0 的实数 叫做二次函数的零点. 所以,求解二次函数的零点,就是求解 二次函数图象与 轴交点的横坐标,也就是求一元二次方程2 + + = 0 的根, 所以零点的可能情况与方程解的情况是相同的.
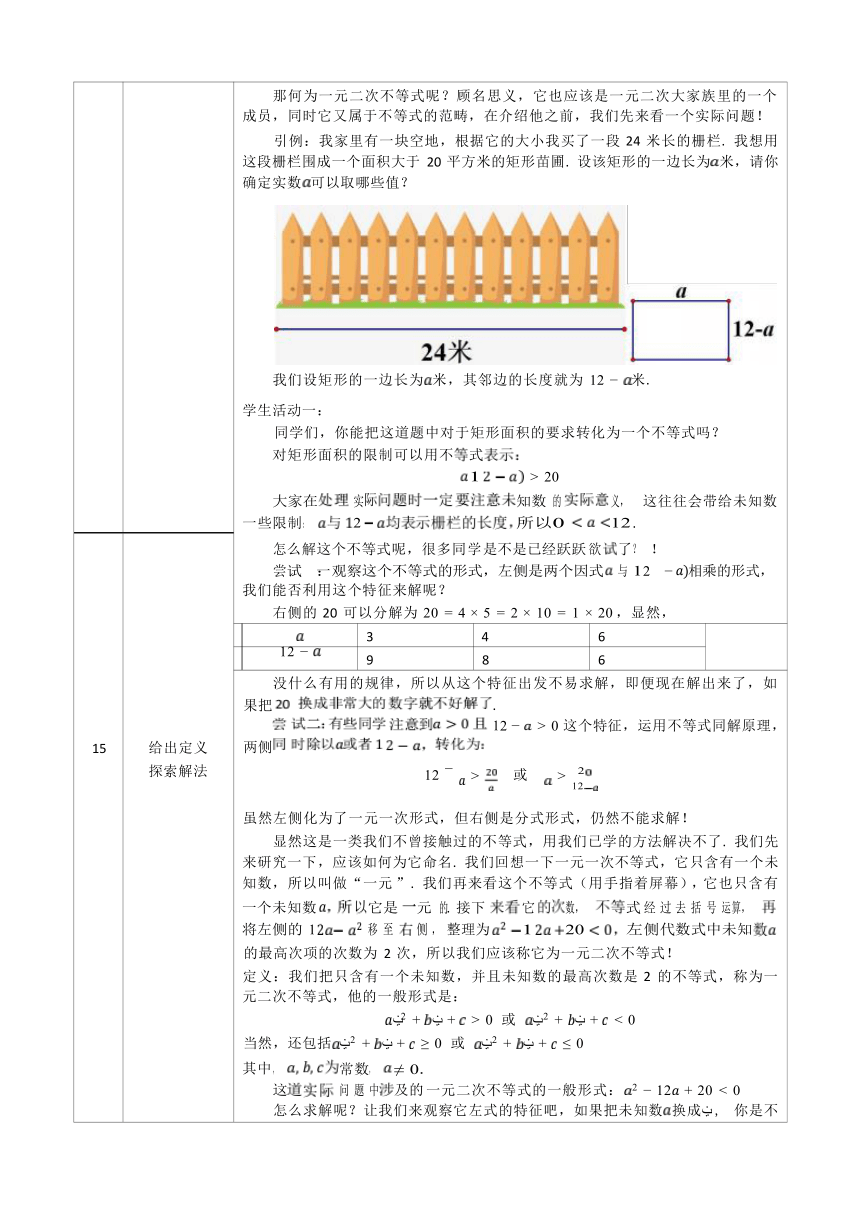
那何为一元二次不等式呢?顾名思义,它也应该是一元二次大家族里的一个 成员,同时它又属于不等式的范畴,在介绍他之前,我们先来看一个实际问题! 引例:我家里有一块空地,根据它的大小我买了一段 24 米长的栅栏. 我想用 这段栅栏围成一个面积大于 20 平方米的矩形苗圃. 设该矩形的一边长为米,请你 确定实数可以取哪些值? 我们设矩形的一边长为米,其邻边的长度就为 12 米. 学生活动一: 同学们,你能把这道题中对于矩形面积的要求转化为一个不等式吗? 对矩形面积的限制可以用不 > 20 一些 . 这往往会带给未知数 解一2! 相乘的形式, 我们能否利用这个特征来解呢? 右侧的 20 可以分解为 20 = 4 × 5 = 2 × 10 = 1 × 20 ,显然,
15 给出定义 探索解法
(
12
) 3 4 6
9 8 6
没什么有用的规律,所以从这个特征出发不易求解,即便现在解出来了,如 2 > 0 这个特征,运用不等式同解原理, 12 > 或 > 1 虽然左侧化为了一元一次形式,但右侧是分式形式,仍然不能求解! 显然这是一类我们不曾接触过的不等式,用我们已学的方法解决不了. 我们先 来研究一下,应该如何为它命名. 我们回想一下一元一次不等式,它只含有一个未 知数,所以叫做“一元 ”. 我们再来看这个不等式(用手指着屏幕),它也只含有 ,的 的最高次项的次数为 2 次,所以我们应该称它为一元二次不等式! 定义:我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一 元二次不等式,他的一般形式是: 2 + + > 0 或 2 + + < 0 当然,还包括2 + + ≥ 0 或 2 + + ≤ 0 其中 一元二次不等式的一般形式: 2 12 + 20 < 0 怎么求解呢?让我们来观察它左式的特征吧,如果把未知数换成 , 你是不
(
是会联想到二次函数
=
2
21
+
02
?那么这二者之间是否存在关联呢?如果
) 你想不到的话,可以换成一次函数 = 12 + 02 与一元一次不等式 12 + 02 < 0, 二者首何先不,联我式,就能是使函2数 值1 2<+00 < 0 ,转化为二次函 数,就是求解自变量 取哪些值能使函数值 < 0. 这时,我们自然会想到利用二次 函数的图象. 右图是这个二次函数的图象,很显然, 自变量 在这一范围(用手指着屏幕比 划)内取值时,函数值 < 0. 由图可知, 的可能取值有无穷多个,不可能一一求 出,要想表达 的取值范围,必须求出这个范围的边界值! 如何求解边界值呢? 我想这可难不倒聪明的同学们,对不对?这些边界值正是二次函数的零点值, 也是,边界值. 求根公式: 1 = 12 64 = 2 ,2 = = 10, 所以边界值为1 = 2 ,2 = 10, 所以不等式的解集为 2 < < 10 . 答:这个矩形苗圃的边长取大于 2 且小于 10 的数时,苗圃的面积会大于 20 平方米. 学生活动二: 借助这个例题,我们认识了一种新的不等式—一元二次不等式,并且尝试利 用二次函数与一元二次方程解出了它的解集. 同学们,现在你们能否自己写出一个 一元二次不等式并把它解出来呢? 你们看,我写出了两个一元二次不等式,你能把它们解出来吗? 例(11 求2 下5 列+关6于>0 的一元二次不等式 特分::这设个二不次等函 的 等2 是5 +“>6”,号出其图象,观察图象的哪些特征呢? 解一元开二 与2 点5 + 6 = 0 ,得到二次函数的零点:1 = 2 ,2 = 3, 看函数:2一 的 般图象 写出不等式的解集:<3+ 2+02 <0,二 次项系数为负< 或3> 2值,. 不等号为“< ”号. (
解
1
一
=
,
次
方
2
2
+
2
+
3
=
0
,得到二次函数的零点:
)析::有设两二种次解函法数 , = 2 + 2 + 3 ,绘出其图象,要注意开口是向下的. (
看函数的图象,写出不等式的解集:
>
3
或
<
1
.
)法二: 看设1般二函=数的图象 1,数 方 3写出不等式的解集:> 二次,=0系与变 为象 2 正,+>值开2或, 3口+不向 <3= 号01为同“>,”得号:
学生活动三: 通过这两个例子,我们发现在解一元二次不等式的过程中,二次函数与一元 二次方程起到了举足轻重的作用,更确切地说,我们在二次函数的图象中看出未 知数 的取值范围,利用一元二次方程解出这个范围的边界值. 由此可以看出,二 次函数、一元二次方程、一元二次不等式,这三者是紧密联系在一起的,我们应 该如何描述他们之间的关系呢? 二次函数 = 2 + + ≠ 0〕 一元二次方程: 2 + + = 0 ≠ 0) 一元二次不等式: 2 + + > 0 或 2 + + < 0 , ≠ 0 通过每一个二次函数,我们可以构造与之对应的一元二次方程与一元二次不 等式,它们左侧的代数式与函数的解析式是完全相同的. 从这个角度来说,方程本 质上就是在解自变量取何值时函数值等于零,对应的就是二次函数的零点,不等 式就是在解自变量取何值时函数值大于零或小于零,不等式解集的边界值就是二 次函数的零点,也就是方程的解,方程与不等式合在一起解决了自变量取何值时 函数值为正、为零、为负的问题! 从这个角度思考,在解一元二次不等式时,我们回归到二次函数是很自然的 事情啊!二次函数是本质嘛! 接下来,我们就尝试初步得出一元二次不等式的通用解法: 对于一元二次不等式2 + + > 0 或 2 + + < 0 ≠ 0, 第一步,我们设二次函数 = 2 + + ≠ 0) 不难,下,转 形,只需改变不等号的方向. 所以在这里我们只需归纳概括 一元二次不等式2 + + > 0 或 2 + + < 0 > 0) 的通用解法. 第二步,通过解一元二次方程: 2 + + = 0 > 0解出二次函数的零点. 前 面的例题都是有两个不等实根的情形,请同学们回忆一下,实际上一元二次方程 的解有几种情况啊? 当 > 0 时,方程有两个不相等的实根,1 = 2+ , 2 = 2 ; 当 = 0 时,方程有两个相等的实根,1 = 2 = ; 当 < 0 时,方程无实根,函数无零点. 那么这三种情况下,不等式的解集分别是什么呢? 请各位同学完成下表: 一元二次不等式2 + + > 0 或 2 + + < 0 > 0的解集的一般性结 论
判别式 = 2 4 > 0 = 0 < 0
练习 总结与提升 二次函数 = 2 + + 的图象 O (
O
) (
L
=
) (
O
) 一元二次方程 2 + + = 0 的根2,1 = 2± (不妨设1 < 2 ) 1 = 2 = 无实根2 + + > 0 的解集 < 1 或 > 2 ≠R2 + + < 0 的解集 1 < < 2
练习(求1:下二2 列关 于 的1=9元02 二 次6 不+等1式 (
3
) (
1
)开口向上, = 36 4 × 9 = 0 ,零点为 = 观察函数图象,得到不等式的解集为: ≠ (
开口向上,
=
4 4
× 3
<
0
,无零点
)2:)设 函 02 2 + 3 观察函数图象,得到不等式的解集为: ∈ 回归二次函数,求解一元二次不等式的方法是不是非常神奇呢?解一个不等 式的过程竟然用到了函数的图象. 有些同学们肯定联想到了什么,请大家也想一 想,在初中,咱们还遇到过哪三个数学概念间有类似的联系?与本节课内容非常 相似,只不过不是一元二次的! 正确,就是一次函数、一元一次方程、一元一次不等式这三者的关系! 一次函数 = + ≠ 0 一元一次方程: + = 0 ≠ 0 一元一次不等式: + > 0 或 + < 0 , ≠ 0 一元一次方程的根正是一次函数的零点,我们也可以通过观察一次函数的图 象得到一元一次不等式的解集!数学竟然这么奇妙,不仅函数有函数的体系,方 程有方程的体系,不等式有不等式的体系,同种类型的函数、方程、不等式之间 竟然也有如此紧密的联系,数学是一个整体,是一张严谨密不透风的网,是一个 完整的体系!我们要穷尽一生去发现其中的奥秘!
2
1
教学目标
教学目标: 1. 经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义; 2. 理解一元二次不等式与相应函数、方程的联系,认识到函数的重要性,体会数学的整体性; 3. 能够体会归纳,概括的方法,把握三者之间的内在联系,借助二次函数,求解一元二次不等式,渗 透数学建模的素养,提升数学运算素养. 教学重点: 从函数的观点看一元二次方程、一元二次不等式,在建立二次函数与一元二次方程、不等式的联系中, 获得用二次函数求解一元二次不等式的一般性方法. 教学难点: 从函数的观点看一元二次方程、一元二次不等式,并归纳概括出一元二次不等式的一般性解法.
教学过程
时间 教学环节 主要师生活动
5 引入 同学们,大家好,今天我们来一起学习第二章第三节,二次函数与一元二次 方程、不等式. 二次函数与一元二次方程我们已在初中学过,你还记得它们吗? 我们先来复习二次函数 = 2 + + ≠ 0的图象及性质: 这条 条轴抛是物否线交开以口及向交上点或可者以向由下判) 2 轴4对, 当 > 0 时,这条抛物线与 轴有两个不同的交点; 当 = 0 时,这条抛物线与 轴有且仅有一个交点; 当 < 0 时,这条抛物线与 轴无交点; 那么我们如何求解交点的横坐标呢? 借助一元二次方程: 2 + + = 0 ≠ 0 当1 => 0 22 4二,次2 方=程 有两个不相 22 4 等的实根 当 = 0 时,一元二次方程有两个相等的实根:1 = 2 = 当 < 0 时,方程无实根. 下面我给出一个新的定义,二次函数的零点. 二次函数的零点:一般地,对于二次函数 = 2 + + ,我们把使2 + + = 0 的实数 叫做二次函数的零点. 所以,求解二次函数的零点,就是求解 二次函数图象与 轴交点的横坐标,也就是求一元二次方程2 + + = 0 的根, 所以零点的可能情况与方程解的情况是相同的.
那何为一元二次不等式呢?顾名思义,它也应该是一元二次大家族里的一个 成员,同时它又属于不等式的范畴,在介绍他之前,我们先来看一个实际问题! 引例:我家里有一块空地,根据它的大小我买了一段 24 米长的栅栏. 我想用 这段栅栏围成一个面积大于 20 平方米的矩形苗圃. 设该矩形的一边长为米,请你 确定实数可以取哪些值? 我们设矩形的一边长为米,其邻边的长度就为 12 米. 学生活动一: 同学们,你能把这道题中对于矩形面积的要求转化为一个不等式吗? 对矩形面积的限制可以用不 > 20 一些 . 这往往会带给未知数 解一2! 相乘的形式, 我们能否利用这个特征来解呢? 右侧的 20 可以分解为 20 = 4 × 5 = 2 × 10 = 1 × 20 ,显然,
15 给出定义 探索解法
(
12
) 3 4 6
9 8 6
没什么有用的规律,所以从这个特征出发不易求解,即便现在解出来了,如 2 > 0 这个特征,运用不等式同解原理, 12 > 或 > 1 虽然左侧化为了一元一次形式,但右侧是分式形式,仍然不能求解! 显然这是一类我们不曾接触过的不等式,用我们已学的方法解决不了. 我们先 来研究一下,应该如何为它命名. 我们回想一下一元一次不等式,它只含有一个未 知数,所以叫做“一元 ”. 我们再来看这个不等式(用手指着屏幕),它也只含有 ,的 的最高次项的次数为 2 次,所以我们应该称它为一元二次不等式! 定义:我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一 元二次不等式,他的一般形式是: 2 + + > 0 或 2 + + < 0 当然,还包括2 + + ≥ 0 或 2 + + ≤ 0 其中 一元二次不等式的一般形式: 2 12 + 20 < 0 怎么求解呢?让我们来观察它左式的特征吧,如果把未知数换成 , 你是不
(
是会联想到二次函数
=
2
21
+
02
?那么这二者之间是否存在关联呢?如果
) 你想不到的话,可以换成一次函数 = 12 + 02 与一元一次不等式 12 + 02 < 0, 二者首何先不,联我式,就能是使函2数 值1 2<+00 < 0 ,转化为二次函 数,就是求解自变量 取哪些值能使函数值 < 0. 这时,我们自然会想到利用二次 函数的图象. 右图是这个二次函数的图象,很显然, 自变量 在这一范围(用手指着屏幕比 划)内取值时,函数值 < 0. 由图可知, 的可能取值有无穷多个,不可能一一求 出,要想表达 的取值范围,必须求出这个范围的边界值! 如何求解边界值呢? 我想这可难不倒聪明的同学们,对不对?这些边界值正是二次函数的零点值, 也是,边界值. 求根公式: 1 = 12 64 = 2 ,2 = = 10, 所以边界值为1 = 2 ,2 = 10, 所以不等式的解集为 2 < < 10 . 答:这个矩形苗圃的边长取大于 2 且小于 10 的数时,苗圃的面积会大于 20 平方米. 学生活动二: 借助这个例题,我们认识了一种新的不等式—一元二次不等式,并且尝试利 用二次函数与一元二次方程解出了它的解集. 同学们,现在你们能否自己写出一个 一元二次不等式并把它解出来呢? 你们看,我写出了两个一元二次不等式,你能把它们解出来吗? 例(11 求2 下5 列+关6于>0 的一元二次不等式 特分::这设个二不次等函 的 等2 是5 +“>6”,号出其图象,观察图象的哪些特征呢? 解一元开二 与2 点5 + 6 = 0 ,得到二次函数的零点:1 = 2 ,2 = 3, 看函数:2一 的 般图象 写出不等式的解集:<3+ 2+02 <0,二 次项系数为负< 或3> 2值,. 不等号为“< ”号. (
解
1
一
=
,
次
方
2
2
+
2
+
3
=
0
,得到二次函数的零点:
)析::有设两二种次解函法数 , = 2 + 2 + 3 ,绘出其图象,要注意开口是向下的. (
看函数的图象,写出不等式的解集:
>
3
或
<
1
.
)法二: 看设1般二函=数的图象 1,数 方 3写出不等式的解集:> 二次,=0系与变 为象 2 正,+>值开2或, 3口+不向 <3= 号01为同“>,”得号:
学生活动三: 通过这两个例子,我们发现在解一元二次不等式的过程中,二次函数与一元 二次方程起到了举足轻重的作用,更确切地说,我们在二次函数的图象中看出未 知数 的取值范围,利用一元二次方程解出这个范围的边界值. 由此可以看出,二 次函数、一元二次方程、一元二次不等式,这三者是紧密联系在一起的,我们应 该如何描述他们之间的关系呢? 二次函数 = 2 + + ≠ 0〕 一元二次方程: 2 + + = 0 ≠ 0) 一元二次不等式: 2 + + > 0 或 2 + + < 0 , ≠ 0 通过每一个二次函数,我们可以构造与之对应的一元二次方程与一元二次不 等式,它们左侧的代数式与函数的解析式是完全相同的. 从这个角度来说,方程本 质上就是在解自变量取何值时函数值等于零,对应的就是二次函数的零点,不等 式就是在解自变量取何值时函数值大于零或小于零,不等式解集的边界值就是二 次函数的零点,也就是方程的解,方程与不等式合在一起解决了自变量取何值时 函数值为正、为零、为负的问题! 从这个角度思考,在解一元二次不等式时,我们回归到二次函数是很自然的 事情啊!二次函数是本质嘛! 接下来,我们就尝试初步得出一元二次不等式的通用解法: 对于一元二次不等式2 + + > 0 或 2 + + < 0 ≠ 0, 第一步,我们设二次函数 = 2 + + ≠ 0) 不难,下,转 形,只需改变不等号的方向. 所以在这里我们只需归纳概括 一元二次不等式2 + + > 0 或 2 + + < 0 > 0) 的通用解法. 第二步,通过解一元二次方程: 2 + + = 0 > 0解出二次函数的零点. 前 面的例题都是有两个不等实根的情形,请同学们回忆一下,实际上一元二次方程 的解有几种情况啊? 当 > 0 时,方程有两个不相等的实根,1 = 2+ , 2 = 2 ; 当 = 0 时,方程有两个相等的实根,1 = 2 = ; 当 < 0 时,方程无实根,函数无零点. 那么这三种情况下,不等式的解集分别是什么呢? 请各位同学完成下表: 一元二次不等式2 + + > 0 或 2 + + < 0 > 0的解集的一般性结 论
判别式 = 2 4 > 0 = 0 < 0
练习 总结与提升 二次函数 = 2 + + 的图象 O (
O
) (
L
=
) (
O
) 一元二次方程 2 + + = 0 的根2,1 = 2± (不妨设1 < 2 ) 1 = 2 = 无实根2 + + > 0 的解集 < 1 或 > 2 ≠R2 + + < 0 的解集 1 < < 2
练习(求1:下二2 列关 于 的1=9元02 二 次6 不+等1式 (
3
) (
1
)开口向上, = 36 4 × 9 = 0 ,零点为 = 观察函数图象,得到不等式的解集为: ≠ (
开口向上,
=
4 4
× 3
<
0
,无零点
)2:)设 函 02 2 + 3 观察函数图象,得到不等式的解集为: ∈ 回归二次函数,求解一元二次不等式的方法是不是非常神奇呢?解一个不等 式的过程竟然用到了函数的图象. 有些同学们肯定联想到了什么,请大家也想一 想,在初中,咱们还遇到过哪三个数学概念间有类似的联系?与本节课内容非常 相似,只不过不是一元二次的! 正确,就是一次函数、一元一次方程、一元一次不等式这三者的关系! 一次函数 = + ≠ 0 一元一次方程: + = 0 ≠ 0 一元一次不等式: + > 0 或 + < 0 , ≠ 0 一元一次方程的根正是一次函数的零点,我们也可以通过观察一次函数的图 象得到一元一次不等式的解集!数学竟然这么奇妙,不仅函数有函数的体系,方 程有方程的体系,不等式有不等式的体系,同种类型的函数、方程、不等式之间 竟然也有如此紧密的联系,数学是一个整体,是一张严谨密不透风的网,是一个 完整的体系!我们要穷尽一生去发现其中的奥秘!
2
1
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
