2014-2015学年高中人教A版数学选修2-2同步课件 2.1.1合情推理
文档属性
| 名称 | 2014-2015学年高中人教A版数学选修2-2同步课件 2.1.1合情推理 |  | |
| 格式 | zip | ||
| 文件大小 | 524.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-03 08:53:29 | ||
图片预览






文档简介
课件17张PPT。没有大胆的猜想,就作不出伟大的发现
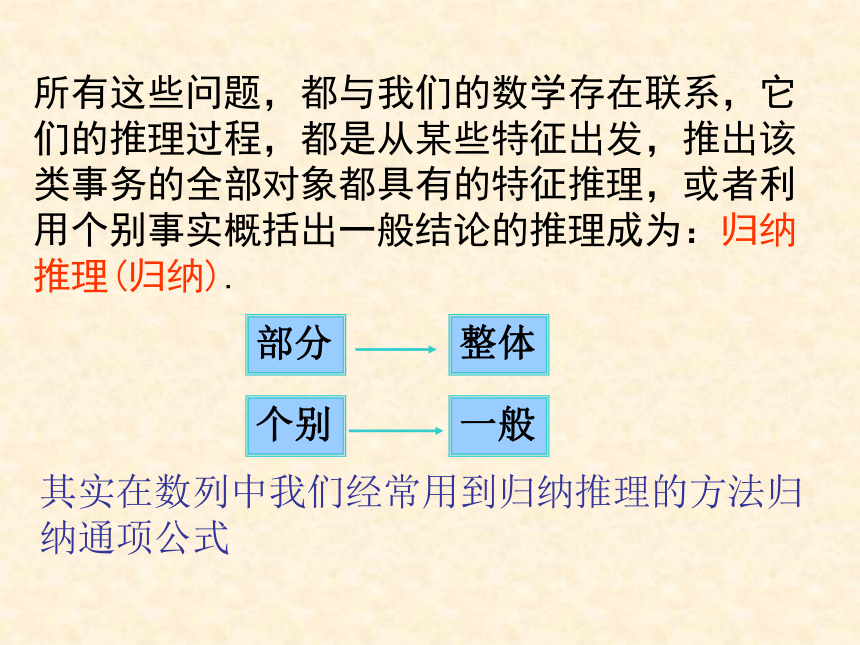
--牛顿合情推理哥德巴赫猜想哥德巴赫(1690-1764),德国人,1742年6月7日写信给大数学家欧拉,提出一个猜想:每一个大于2的偶数都可以表示为两个素数的和(或每一个大于或等于6的偶数都可表示为两个奇素数的和).同年6月30日欧拉回信表示他虽不能证明此猜想,但他相信这是完全正确的.这就是著名的哥德巴赫猜想(Goldbach‘s Conjecture) “1+1=2”费马猜想(Fermat‘s conjecture)又称费马大定理或费马问题,是数论中最著名的世界难题之一.1637年,法国数学家费马在巴歇校订的希腊数学家丢番图的《算术》第II卷第8命题旁边写道:“将一个立方数分为两个立方数,一个四次幂分为两个四次幂,或者一般地将一个高于二次的幂分为两个同次的幂,这是不可能的.关于此,我确信已发现一种美妙的证法,可惜这里空白的地方太小,写不下.”费马去世后,人们找不到这个猜想的证明,由此激发起许多数学家的兴趣.欧拉、勒让德、高斯、阿贝尔、狄利克雷、柯西等大数学家都试证过,但谁也没有得到普遍的证法.300多年以来,无数优秀学者为证明这个猜想,付出了巨大精力,同时亦产生出不少重要的数学概念及分支. 若用不定方程来表示,费马大定理即:当n > 2时,不定方程xn + y n = z n 没有xyz≠0的整数解.为了证明这个结果,只需证明方程x4 + y 4 = z 4 ,(x , y) = 1和方程xp + yp = zp ,(x , y) = (x , z) = (y , z) = 1﹝p是一个奇素数﹞均无xyz≠0的整数解 法国数学家Fermat在17世纪提出的数论领域猜想,之后的300多年中,人们既证明不了,又否定不了.1993年,英国数学家Andrew Wiles攻破了费马猜想 1852年英国伦敦大学教授狄·摩根的学生古特里向他提了一个问题:在一切平面图形上,是否总可以用四种颜色着色,就可以使每两个相邻部分的颜色都不相同呢?假如说,必要的颜色最大数是4,那又该如何证明呢?——这就是四色问题的起源 在100多年后的1976年被美国伊利诺大学的阿佩尔和哈肯二人在电子计算机的辅助下证明了四色定理 8世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上有7座桥,将河中的两个岛和河岸连结,如图1所示.城中的居民经常沿河过桥散步,于是提出了一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点.这就是七桥问题,一个著名的图论问题所有这些问题,都与我们的数学存在联系,它们的推理过程,都是从某些特征出发,推出该类事务的全部对象都具有的特征推理,或者利用个别事实概括出一般结论的推理成为:归纳推理(归纳).部分整体个别一般其实在数列中我们经常用到归纳推理的方法归纳通项公式猜想这个数学通项公式为当然,归纳推理得出的结论,我们还需要对它们进行严格定义上的证明,它为我们的研究提供了一种方向.除了归纳,人们在创造活动中,类比思想也是一种很重要的思想.生物?这种有两类对象具有某些类似特征,由其中的已知对象特征,推出另一类对象也具有这些特征的推理方法叫做类比推理(类比).Do not neglect analogies,they may lead to discovery. Analogy? is? another? fertile? source? of discovery
---Polya“格物究理,非要究尽天下之物,但于一事上究尽,其他可以类推” . --程颐“我珍惜类比胜于任何别的东西,它是我最可信赖的老师”.
--开普勒例2. 利用实数的加法和乘法的运算性质,列出它们的相似的运算性质.例3 在平面几何里,有勾股定理:设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2.拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面面积间的关系,可以得出的结论是:设三棱锥P-DEF的三个侧面PED, PEF,PDF两两垂直, 则_________________________练习具体问题观察、联想、
比较、分析归纳、类比猜想合情推理
(plausible reasoning)2.请你数一下上表中每一个多面体具有的顶点数(V)、棱数(E)、和面数(F),并把结果记入下表中,你会有惊奇的发现什么? 1.合情推理是数学发展的动力,科学发现的先导.促进数学的发展,也促进数学方法的研究,数学史上一些著名的发现,如欧拉公式的发现就得益于合情推理.可见合情推理对数学的研究和发展,起了积极的推动作用.2.合情推理是实现问题解决的一种重要的思维方法,是创新思维的重要组成部分 .说明练习3.查阅有关汉若塔游戏的问题,结合课本P75~77说明移动次数最少的公式的由来.4.查阅有关费尔马大定理的资料,想象他的推理思想.
--牛顿合情推理哥德巴赫猜想哥德巴赫(1690-1764),德国人,1742年6月7日写信给大数学家欧拉,提出一个猜想:每一个大于2的偶数都可以表示为两个素数的和(或每一个大于或等于6的偶数都可表示为两个奇素数的和).同年6月30日欧拉回信表示他虽不能证明此猜想,但他相信这是完全正确的.这就是著名的哥德巴赫猜想(Goldbach‘s Conjecture) “1+1=2”费马猜想(Fermat‘s conjecture)又称费马大定理或费马问题,是数论中最著名的世界难题之一.1637年,法国数学家费马在巴歇校订的希腊数学家丢番图的《算术》第II卷第8命题旁边写道:“将一个立方数分为两个立方数,一个四次幂分为两个四次幂,或者一般地将一个高于二次的幂分为两个同次的幂,这是不可能的.关于此,我确信已发现一种美妙的证法,可惜这里空白的地方太小,写不下.”费马去世后,人们找不到这个猜想的证明,由此激发起许多数学家的兴趣.欧拉、勒让德、高斯、阿贝尔、狄利克雷、柯西等大数学家都试证过,但谁也没有得到普遍的证法.300多年以来,无数优秀学者为证明这个猜想,付出了巨大精力,同时亦产生出不少重要的数学概念及分支. 若用不定方程来表示,费马大定理即:当n > 2时,不定方程xn + y n = z n 没有xyz≠0的整数解.为了证明这个结果,只需证明方程x4 + y 4 = z 4 ,(x , y) = 1和方程xp + yp = zp ,(x , y) = (x , z) = (y , z) = 1﹝p是一个奇素数﹞均无xyz≠0的整数解 法国数学家Fermat在17世纪提出的数论领域猜想,之后的300多年中,人们既证明不了,又否定不了.1993年,英国数学家Andrew Wiles攻破了费马猜想 1852年英国伦敦大学教授狄·摩根的学生古特里向他提了一个问题:在一切平面图形上,是否总可以用四种颜色着色,就可以使每两个相邻部分的颜色都不相同呢?假如说,必要的颜色最大数是4,那又该如何证明呢?——这就是四色问题的起源 在100多年后的1976年被美国伊利诺大学的阿佩尔和哈肯二人在电子计算机的辅助下证明了四色定理 8世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上有7座桥,将河中的两个岛和河岸连结,如图1所示.城中的居民经常沿河过桥散步,于是提出了一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点.这就是七桥问题,一个著名的图论问题所有这些问题,都与我们的数学存在联系,它们的推理过程,都是从某些特征出发,推出该类事务的全部对象都具有的特征推理,或者利用个别事实概括出一般结论的推理成为:归纳推理(归纳).部分整体个别一般其实在数列中我们经常用到归纳推理的方法归纳通项公式猜想这个数学通项公式为当然,归纳推理得出的结论,我们还需要对它们进行严格定义上的证明,它为我们的研究提供了一种方向.除了归纳,人们在创造活动中,类比思想也是一种很重要的思想.生物?这种有两类对象具有某些类似特征,由其中的已知对象特征,推出另一类对象也具有这些特征的推理方法叫做类比推理(类比).Do not neglect analogies,they may lead to discovery. Analogy? is? another? fertile? source? of discovery
---Polya“格物究理,非要究尽天下之物,但于一事上究尽,其他可以类推” . --程颐“我珍惜类比胜于任何别的东西,它是我最可信赖的老师”.
--开普勒例2. 利用实数的加法和乘法的运算性质,列出它们的相似的运算性质.例3 在平面几何里,有勾股定理:设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2.拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面面积间的关系,可以得出的结论是:设三棱锥P-DEF的三个侧面PED, PEF,PDF两两垂直, 则_________________________练习具体问题观察、联想、
比较、分析归纳、类比猜想合情推理
(plausible reasoning)2.请你数一下上表中每一个多面体具有的顶点数(V)、棱数(E)、和面数(F),并把结果记入下表中,你会有惊奇的发现什么? 1.合情推理是数学发展的动力,科学发现的先导.促进数学的发展,也促进数学方法的研究,数学史上一些著名的发现,如欧拉公式的发现就得益于合情推理.可见合情推理对数学的研究和发展,起了积极的推动作用.2.合情推理是实现问题解决的一种重要的思维方法,是创新思维的重要组成部分 .说明练习3.查阅有关汉若塔游戏的问题,结合课本P75~77说明移动次数最少的公式的由来.4.查阅有关费尔马大定理的资料,想象他的推理思想.
