5.4三角函数的图象与性质应用 第一课时 教学设计(表格式)
文档属性
| 名称 | 5.4三角函数的图象与性质应用 第一课时 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 147.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-17 00:26:39 | ||
图片预览

文档简介
课题 三角函数的图象与性质应用(1)
教学目标
教学目标:1.运用三角函数的图象与性质研究较为复杂的函数,进一步认识图象与性质的作用 ; 2.在运用图象与性质解决问题的过程中,体会数形结合的思想方法 ; 3.发展学生直观想象,逻辑推理,数学运算等数学素养. 教学重点:研究图象变换下函数的性质. 教学难点: 由图象观察性质.
教学过程
时间 教学环节 主要师生活动
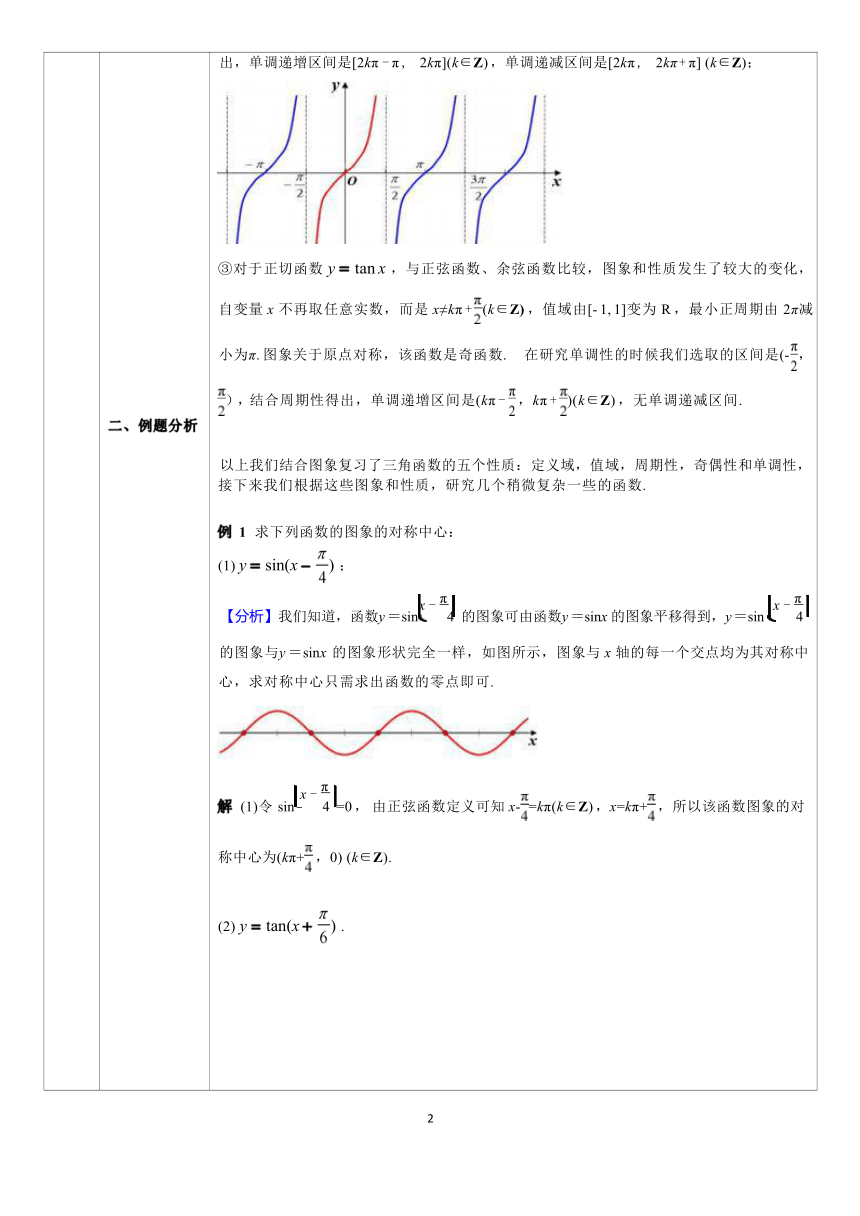
一、复习回顾 我们在前几次课学习了正弦函数、余弦函数和正切函数的图象和性质,大家还记得有哪些 内容吗?让我们结合三角函数的图象一起来回顾一下:
①对于正弦函数 y = sin x ,定义域是 R,最小正周期是 2π , 我们可以先通过五点法画出一 个周期内的简图,五点分别是(0,0), ,1 ,(π , 0), π , - 1 ,(2π , 0). 由图象可以看出最 大值是 1 ,最小值是- 1 ,值域是[- 1, 1].然后将这段图象“复制-粘贴 ”,从而得到整个函数的 图象.我们发现,图象关于原点对称,该函数是奇函数.在研究单调性的时候我们选取的区间 不是[0 ,2π] ,而是[- ,] ,结合周期性得出,单调递增区间是[2kπ - ,2kπ + ](k∈Z), 单调递减区间是[2kπ + ,2kπ + ] (k∈Z). ②对于余弦函数 y = cos x ,其图象可以由正弦函数 y = sin x 的图象向左平移个单位长度 得到,由图象可以看出,该函数的定义域是 R ,值域是[- 1, 1] ,最小正周期是 2π , 图象关于 y 轴对称,该函数是偶函数. 在研究单调性的时候我们选取的区间是[-π , π],结合周期性得
1
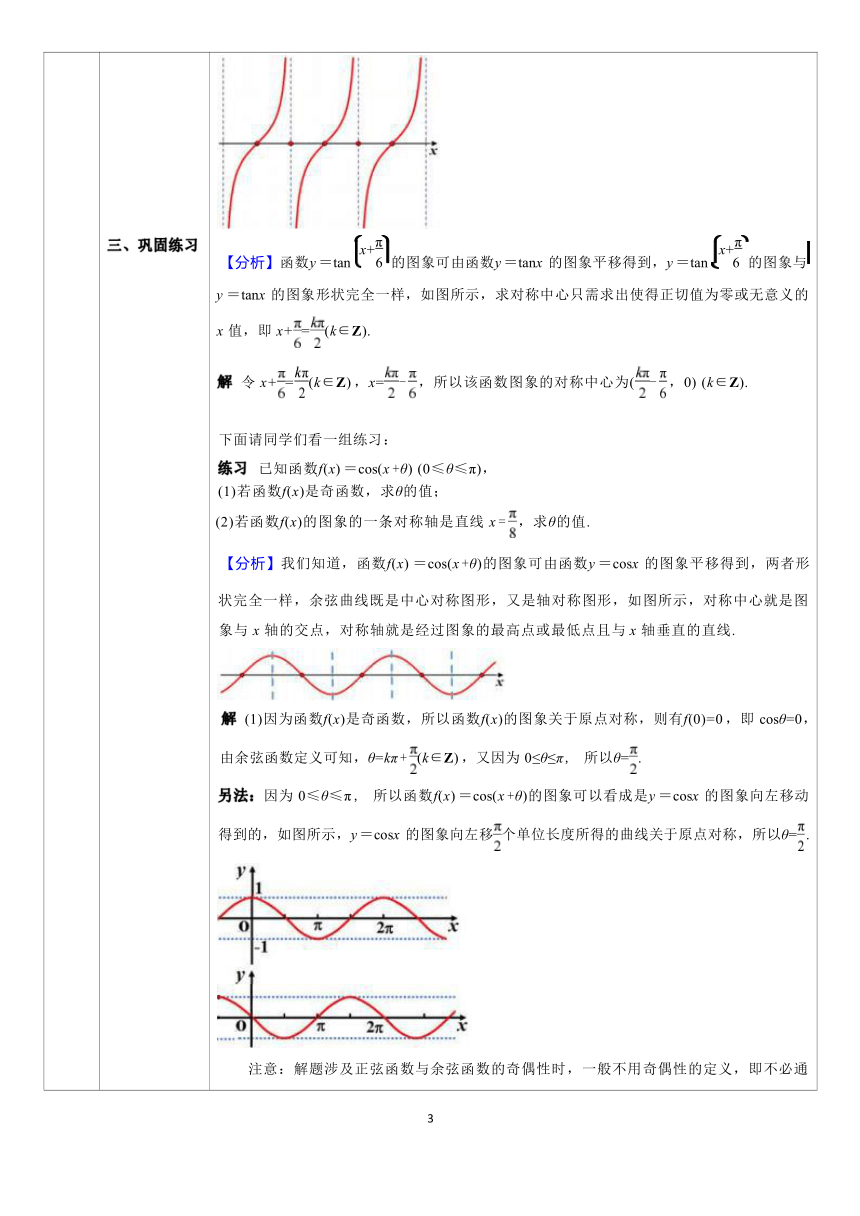
二、例题分析 出,单调递增区间是[2kπ - π , 2kπ](k∈Z) ,单调递减区间是[2kπ , 2kπ + π] (k∈Z); ③对于正切函数 y = tan x ,与正弦函数、余弦函数比较,图象和性质发生了较大的变化, 自变量 x 不再取任意实数,而是 x≠kπ + (k∈Z) ,值域由[- 1, 1]变为 R ,最小正周期由 2π减 小为π. 图象关于原点对称,该函数是奇函数. 在研究单调性的时候我们选取的区间是(-, ),结合周期性得出,单调递增区间是(kπ - ,kπ + )(k∈Z) ,无单调递减区间. 以上我们结合图象复习了三角函数的五个性质:定义域,值域,周期性,奇偶性和单调性, 接下来我们根据这些图象和性质,研究几个稍微复杂一些的函数. 例 1 求下列函数的图象的对称中心: (1) y = sin(x - ) ; (
x
-
π
x
-
π
)【分析】我们知道,函数y =sin 4 的图象可由函数y =sinx 的图象平移得到,y =sin 4 的图象与y =sinx 的图象形状完全一样,如图所示,图象与 x 轴的每一个交点均为其对称中 心,求对称中心只需求出函数的零点即可. (
x
-
π
)解 (1)令 sin 4 =0 , 由正弦函数定义可知 x-=kπ(k∈Z) ,x=kπ+ ,所以该函数图象的对 称中心为(kπ+ ,0) (k∈Z). (2) y = tan(x + ) .
2
三、巩固练习 (
x
+
π
x
+
π
)【分析】函数y =tan 6 的图象可由函数y =tanx 的图象平移得到,y =tan 6 的图象与 y =tanx 的图象形状完全一样,如图所示,求对称中心只需求出使得正切值为零或无意义的 x 值,即 x+=(k∈Z). 解 令 x+=(k∈Z) ,x=- ,所以该函数图象的对称中心为(- ,0) (k∈Z). 下面请同学们看一组练习: 练习 已知函数f(x) =cos(x +θ) (0≤θ≤π), (1)若函数f(x)是奇函数,求θ的值; (2)若函数f(x)的图象的一条对称轴是直线 x = ,求θ的值. 【分析】我们知道,函数f(x) =cos(x +θ)的图象可由函数y =cosx 的图象平移得到,两者形 状完全一样,余弦曲线既是中心对称图形,又是轴对称图形,如图所示,对称中心就是图 象与 x 轴的交点,对称轴就是经过图象的最高点或最低点且与 x 轴垂直的直线. 解 (1)因为函数f(x)是奇函数,所以函数f(x)的图象关于原点对称,则有f(0)=0 ,即 cosθ=0, 由余弦函数定义可知,θ=kπ + (k∈Z) ,又因为 0≤θ≤π , 所以θ= . 另法:因为 0≤θ≤π , 所以函数f(x) =cos(x +θ)的图象可以看成是y =cosx 的图象向左移动 得到的,如图所示,y =cosx 的图象向左移个单位长度所得的曲线关于原点对称,所以θ= . 注意:解题涉及正弦函数与余弦函数的奇偶性时,一般不用奇偶性的定义,即不必通
3
四、拓展应用 过计算考察f(-x)与f(x)的关系,而是根据三角函数图象的特点来解答. (2)因为直线 x = 是函数f(x)的图象的一条对称轴,所以当 x = 时,函数取得最大值或最小 值,即f()=:1 ,cos(+θ)=:1 ,由余弦函数定义可知,+θ=kπ(k∈Z) ,θ=kπ - ,又因为 0≤θ≤π , 所以θ= . 小结:在以上例题和练习的解答过程中,我们根据平移变换下三角函数图象的特点,得到 了求图象对称中心或对称轴的方法. (1)点(a,0)是正弦曲线f(x)=sin(x+θ)的对称中心 f(a)=0; (2)直线 x=a 是正弦曲线f(x)=sin(x+θ)的对称轴 f(a)=:1; (3)点(a,0)是正切曲线f(x)=tan(x+θ)的对称中心 a+θ=(k∈Z). 接下来我们研究翻折变换下三角函数的图象和性质: 例 2 求下列函数的周期与单调区间: (1)y =|cosx|; (2) y =|tanx|. 【分析】 我们看到,两个小题中的三角函数都加了绝对值符号, 由前面的章节可知,将函 数y=f(x)在 x 轴下方的部分图象翻折上去,就得到了函数y=f|(x)|的图象. (1)函数y =|cosx|的图象如下: 由图象可知,该函数的最小正周期是π , 我们先观察一个周期内的图象,选定的区间是[- , ] ,函数在[- ,0]上单调递增,在[0 ,]上单调递减,所以该函数的单调递增区间是[kπ - ,kπ] (k∈Z) ,单调递减区间是[kπ , kπ + ](k∈Z). (2)函数y =|tanx|的图象如下: 由图象可知,该函数的最小正周期是π , 我们先观察一个周期内的图象,选定的区间是(- , ) , 函数在(- ,0]上单调递减,在[0 ,)上单调递增,所以该函数的单调递增区间是
4
五、课堂小结 六、布置作业 kπ , kπ + (k∈Z) ,单调递减区间是 kπ - ,kπ (k∈Z). 小结:求含绝对值的三角函数的单调区间,先画出大致图象确定函数的周期,再选定一个 周期内的图象写出单调区间,最后拓展到整个定义域. 思考 (1)函数y =|cosx|和y =|tanx|的图象具有怎样的对称性呢? 观察函数y =|cosx|的图象可知,该图象是轴对称图形,不是中心对称图形,对称轴方程为 x =(k∈Z). 观察函数y =|tanx|的图象可知,该图象是轴对称图形,不是中心对称图形,对称轴方程也 是 x =(k∈Z). (2)与函数y =|cosx|相比,函数y =|cosx|+1 的性质有变化吗?
y =|cosx|
y =|cosx|+1
----定义域,周期性,单调性,奇偶性,对称轴方程不变,值域由[0,1]变为[1,2]. 本节课研究了平移变换与翻折变换下三角函数图象的对称性、三角函数的周期性和单调性, 进一步认识了图象与性质的作用,体现了数形结合的思想方法. 需要掌握的具体内容如下: (1)点(a,0)是正弦曲线f(x)=sin(x+θ)的对称中心 f(a)=0;(余弦曲线同理) (2)直线 x=a 是正弦曲线f(x)=sin(x+θ)的对称轴 f(a)=:1;(余弦曲线同理)
5
(3)点(a,0)是正切曲线f(x)=tan(x+θ)的对称中心 a+θ=(k∈Z). (4)含绝对值的三角函数的图象和性质的研究方法. 课本第 213-214 页:习题 5.4 第 3 ,6 ,7 ,12 ,19 题.
6
教学目标
教学目标:1.运用三角函数的图象与性质研究较为复杂的函数,进一步认识图象与性质的作用 ; 2.在运用图象与性质解决问题的过程中,体会数形结合的思想方法 ; 3.发展学生直观想象,逻辑推理,数学运算等数学素养. 教学重点:研究图象变换下函数的性质. 教学难点: 由图象观察性质.
教学过程
时间 教学环节 主要师生活动
一、复习回顾 我们在前几次课学习了正弦函数、余弦函数和正切函数的图象和性质,大家还记得有哪些 内容吗?让我们结合三角函数的图象一起来回顾一下:
①对于正弦函数 y = sin x ,定义域是 R,最小正周期是 2π , 我们可以先通过五点法画出一 个周期内的简图,五点分别是(0,0), ,1 ,(π , 0), π , - 1 ,(2π , 0). 由图象可以看出最 大值是 1 ,最小值是- 1 ,值域是[- 1, 1].然后将这段图象“复制-粘贴 ”,从而得到整个函数的 图象.我们发现,图象关于原点对称,该函数是奇函数.在研究单调性的时候我们选取的区间 不是[0 ,2π] ,而是[- ,] ,结合周期性得出,单调递增区间是[2kπ - ,2kπ + ](k∈Z), 单调递减区间是[2kπ + ,2kπ + ] (k∈Z). ②对于余弦函数 y = cos x ,其图象可以由正弦函数 y = sin x 的图象向左平移个单位长度 得到,由图象可以看出,该函数的定义域是 R ,值域是[- 1, 1] ,最小正周期是 2π , 图象关于 y 轴对称,该函数是偶函数. 在研究单调性的时候我们选取的区间是[-π , π],结合周期性得
1
二、例题分析 出,单调递增区间是[2kπ - π , 2kπ](k∈Z) ,单调递减区间是[2kπ , 2kπ + π] (k∈Z); ③对于正切函数 y = tan x ,与正弦函数、余弦函数比较,图象和性质发生了较大的变化, 自变量 x 不再取任意实数,而是 x≠kπ + (k∈Z) ,值域由[- 1, 1]变为 R ,最小正周期由 2π减 小为π. 图象关于原点对称,该函数是奇函数. 在研究单调性的时候我们选取的区间是(-, ),结合周期性得出,单调递增区间是(kπ - ,kπ + )(k∈Z) ,无单调递减区间. 以上我们结合图象复习了三角函数的五个性质:定义域,值域,周期性,奇偶性和单调性, 接下来我们根据这些图象和性质,研究几个稍微复杂一些的函数. 例 1 求下列函数的图象的对称中心: (1) y = sin(x - ) ; (
x
-
π
x
-
π
)【分析】我们知道,函数y =sin 4 的图象可由函数y =sinx 的图象平移得到,y =sin 4 的图象与y =sinx 的图象形状完全一样,如图所示,图象与 x 轴的每一个交点均为其对称中 心,求对称中心只需求出函数的零点即可. (
x
-
π
)解 (1)令 sin 4 =0 , 由正弦函数定义可知 x-=kπ(k∈Z) ,x=kπ+ ,所以该函数图象的对 称中心为(kπ+ ,0) (k∈Z). (2) y = tan(x + ) .
2
三、巩固练习 (
x
+
π
x
+
π
)【分析】函数y =tan 6 的图象可由函数y =tanx 的图象平移得到,y =tan 6 的图象与 y =tanx 的图象形状完全一样,如图所示,求对称中心只需求出使得正切值为零或无意义的 x 值,即 x+=(k∈Z). 解 令 x+=(k∈Z) ,x=- ,所以该函数图象的对称中心为(- ,0) (k∈Z). 下面请同学们看一组练习: 练习 已知函数f(x) =cos(x +θ) (0≤θ≤π), (1)若函数f(x)是奇函数,求θ的值; (2)若函数f(x)的图象的一条对称轴是直线 x = ,求θ的值. 【分析】我们知道,函数f(x) =cos(x +θ)的图象可由函数y =cosx 的图象平移得到,两者形 状完全一样,余弦曲线既是中心对称图形,又是轴对称图形,如图所示,对称中心就是图 象与 x 轴的交点,对称轴就是经过图象的最高点或最低点且与 x 轴垂直的直线. 解 (1)因为函数f(x)是奇函数,所以函数f(x)的图象关于原点对称,则有f(0)=0 ,即 cosθ=0, 由余弦函数定义可知,θ=kπ + (k∈Z) ,又因为 0≤θ≤π , 所以θ= . 另法:因为 0≤θ≤π , 所以函数f(x) =cos(x +θ)的图象可以看成是y =cosx 的图象向左移动 得到的,如图所示,y =cosx 的图象向左移个单位长度所得的曲线关于原点对称,所以θ= . 注意:解题涉及正弦函数与余弦函数的奇偶性时,一般不用奇偶性的定义,即不必通
3
四、拓展应用 过计算考察f(-x)与f(x)的关系,而是根据三角函数图象的特点来解答. (2)因为直线 x = 是函数f(x)的图象的一条对称轴,所以当 x = 时,函数取得最大值或最小 值,即f()=:1 ,cos(+θ)=:1 ,由余弦函数定义可知,+θ=kπ(k∈Z) ,θ=kπ - ,又因为 0≤θ≤π , 所以θ= . 小结:在以上例题和练习的解答过程中,我们根据平移变换下三角函数图象的特点,得到 了求图象对称中心或对称轴的方法. (1)点(a,0)是正弦曲线f(x)=sin(x+θ)的对称中心 f(a)=0; (2)直线 x=a 是正弦曲线f(x)=sin(x+θ)的对称轴 f(a)=:1; (3)点(a,0)是正切曲线f(x)=tan(x+θ)的对称中心 a+θ=(k∈Z). 接下来我们研究翻折变换下三角函数的图象和性质: 例 2 求下列函数的周期与单调区间: (1)y =|cosx|; (2) y =|tanx|. 【分析】 我们看到,两个小题中的三角函数都加了绝对值符号, 由前面的章节可知,将函 数y=f(x)在 x 轴下方的部分图象翻折上去,就得到了函数y=f|(x)|的图象. (1)函数y =|cosx|的图象如下: 由图象可知,该函数的最小正周期是π , 我们先观察一个周期内的图象,选定的区间是[- , ] ,函数在[- ,0]上单调递增,在[0 ,]上单调递减,所以该函数的单调递增区间是[kπ - ,kπ] (k∈Z) ,单调递减区间是[kπ , kπ + ](k∈Z). (2)函数y =|tanx|的图象如下: 由图象可知,该函数的最小正周期是π , 我们先观察一个周期内的图象,选定的区间是(- , ) , 函数在(- ,0]上单调递减,在[0 ,)上单调递增,所以该函数的单调递增区间是
4
五、课堂小结 六、布置作业 kπ , kπ + (k∈Z) ,单调递减区间是 kπ - ,kπ (k∈Z). 小结:求含绝对值的三角函数的单调区间,先画出大致图象确定函数的周期,再选定一个 周期内的图象写出单调区间,最后拓展到整个定义域. 思考 (1)函数y =|cosx|和y =|tanx|的图象具有怎样的对称性呢? 观察函数y =|cosx|的图象可知,该图象是轴对称图形,不是中心对称图形,对称轴方程为 x =(k∈Z). 观察函数y =|tanx|的图象可知,该图象是轴对称图形,不是中心对称图形,对称轴方程也 是 x =(k∈Z). (2)与函数y =|cosx|相比,函数y =|cosx|+1 的性质有变化吗?
y =|cosx|
y =|cosx|+1
----定义域,周期性,单调性,奇偶性,对称轴方程不变,值域由[0,1]变为[1,2]. 本节课研究了平移变换与翻折变换下三角函数图象的对称性、三角函数的周期性和单调性, 进一步认识了图象与性质的作用,体现了数形结合的思想方法. 需要掌握的具体内容如下: (1)点(a,0)是正弦曲线f(x)=sin(x+θ)的对称中心 f(a)=0;(余弦曲线同理) (2)直线 x=a 是正弦曲线f(x)=sin(x+θ)的对称轴 f(a)=:1;(余弦曲线同理)
5
(3)点(a,0)是正切曲线f(x)=tan(x+θ)的对称中心 a+θ=(k∈Z). (4)含绝对值的三角函数的图象和性质的研究方法. 课本第 213-214 页:习题 5.4 第 3 ,6 ,7 ,12 ,19 题.
6
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
