18.2.2菱形课件
图片预览






文档简介
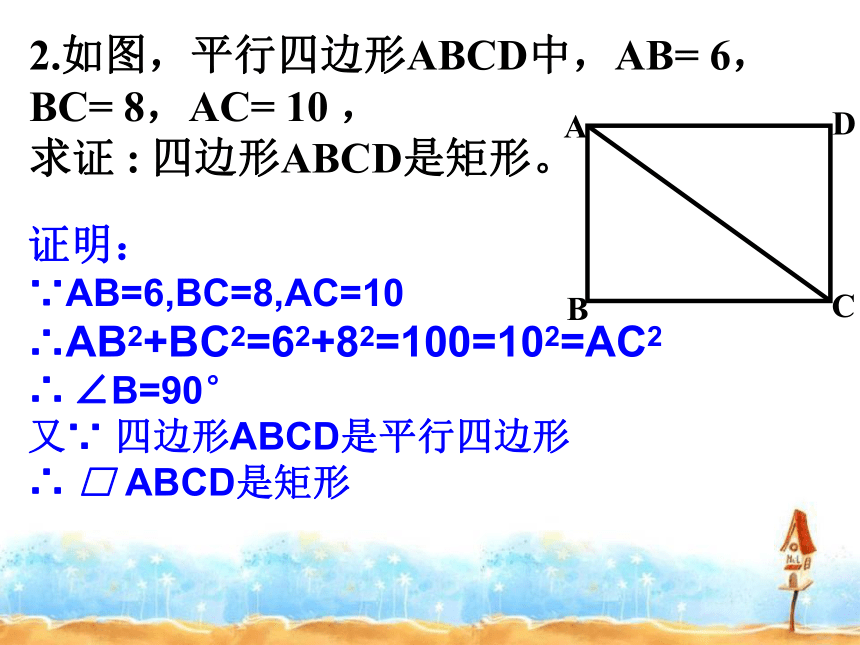
课件33张PPT。复习回顾:矩形的判定方法有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。有三个角是直角的四边形是矩形 。判定定理1:判定定理2:判定定理3:11种5种5种1种练习.1、下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX2.如图,平行四边形ABCD中,AB= 6,BC= 8,AC= 10 ,
求证 : 四边形ABCD是矩形。证明:
∵AB=6,BC=8,AC=10
∴AB2+BC2=62+82=100=102=AC2
∴ ∠B=90°
又∵ 四边形ABCD是平行四边形
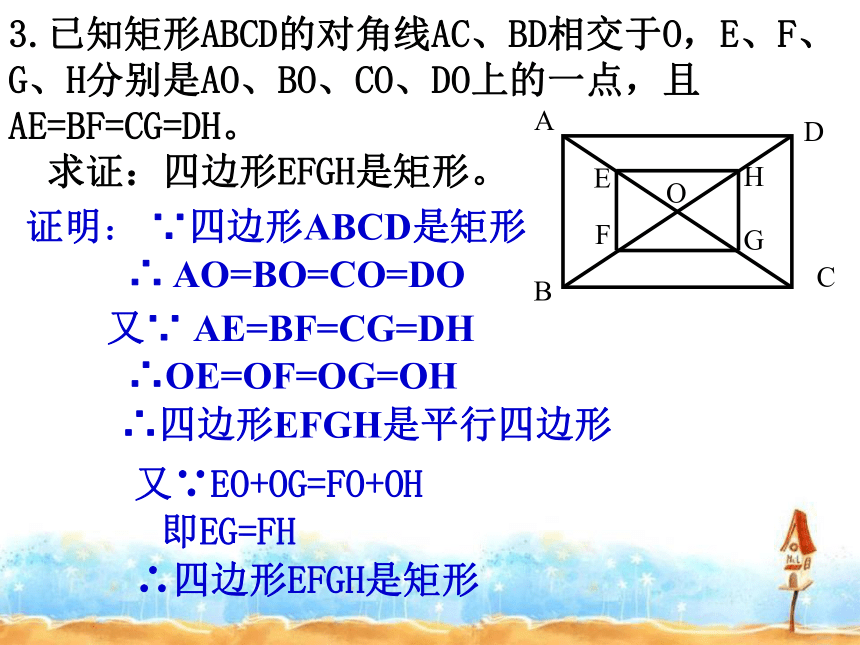
∴ □ ABCD是矩形3.已知矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH。
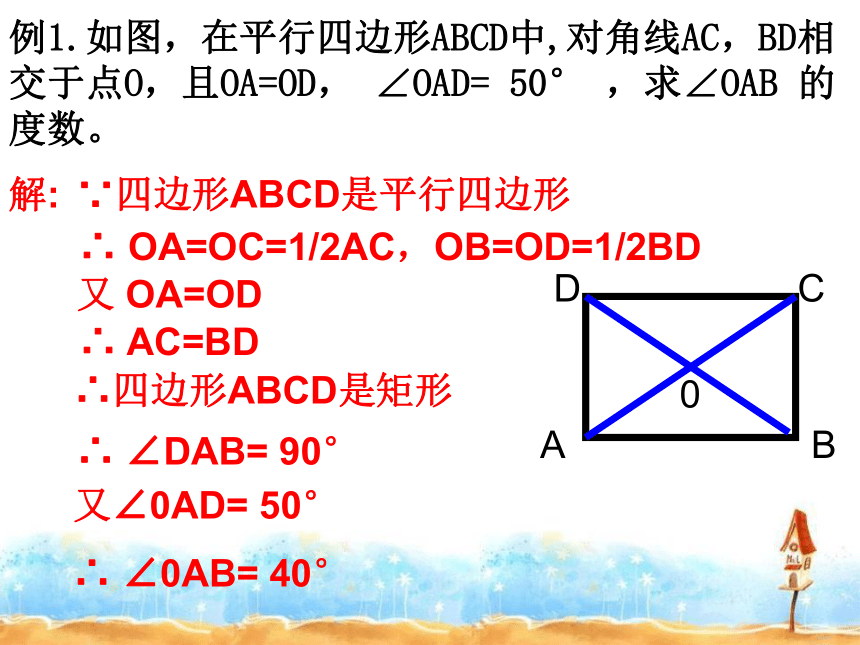
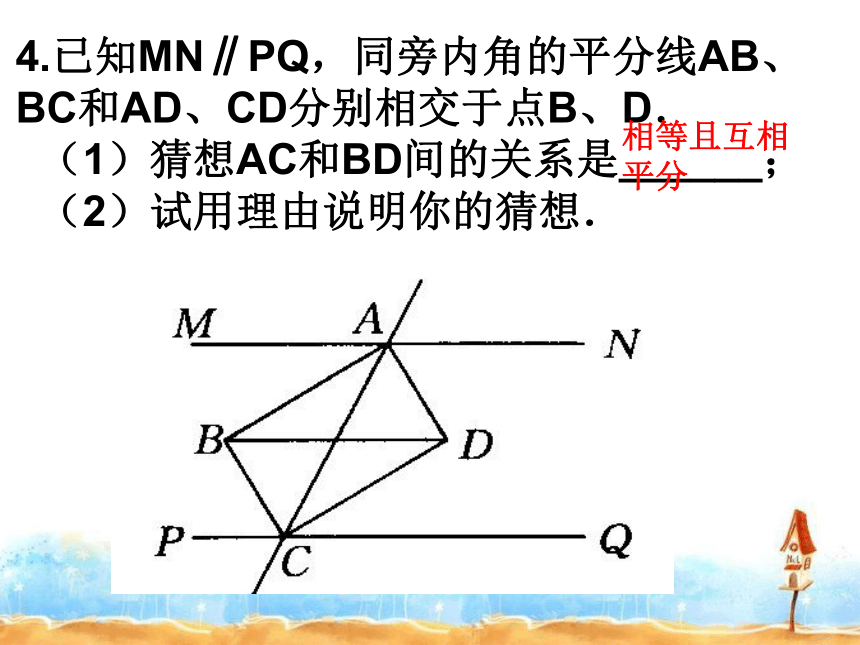
求证:四边形EFGH是矩形。证明: ∵四边形ABCD是矩形∴ AO=BO=CO=DO又∵ AE=BF=CG=DH∴OE=OF=OG=OH∴四边形EFGH是平行四边形又∵EO+OG=FO+OH即EG=FH∴四边形EFGH是矩形例1.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,且OA=OD, ∠OAD= 50° ,求∠OAB 的度数。解: ∵四边形ABCD是平行四边形∴ OA=OC=1/2AC,OB=OD=1/2BD 又 OA=OD∴ AC=BD∴四边形ABCD是矩形∴ ∠DAB= 90°又∠0AD= 50°∴ ∠0AB= 40°4.已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是______;
(2)试用理由说明你的猜想.相等且互相平分18.2.2菱形(1) 学习目标:
1.理解菱形的概念;
2.会用菱形的性质解决简单的问题;
3.经历类比矩形探究菱形性质的过程,通过观察、类比、猜想、证明,体会几何图形探究的一般步骤和方法;
学习重难点:
重点:菱形性质的探索、证明与应用两组对边
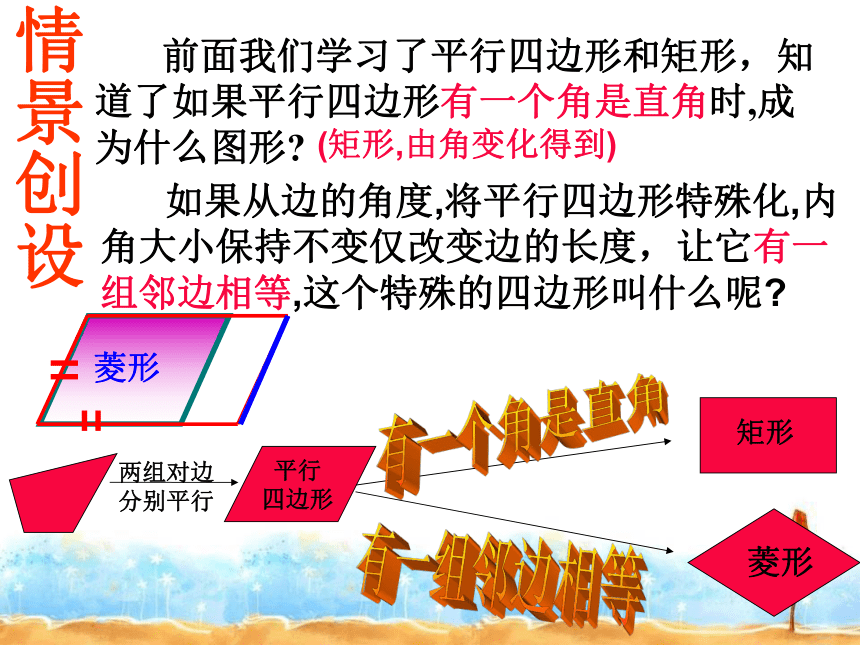
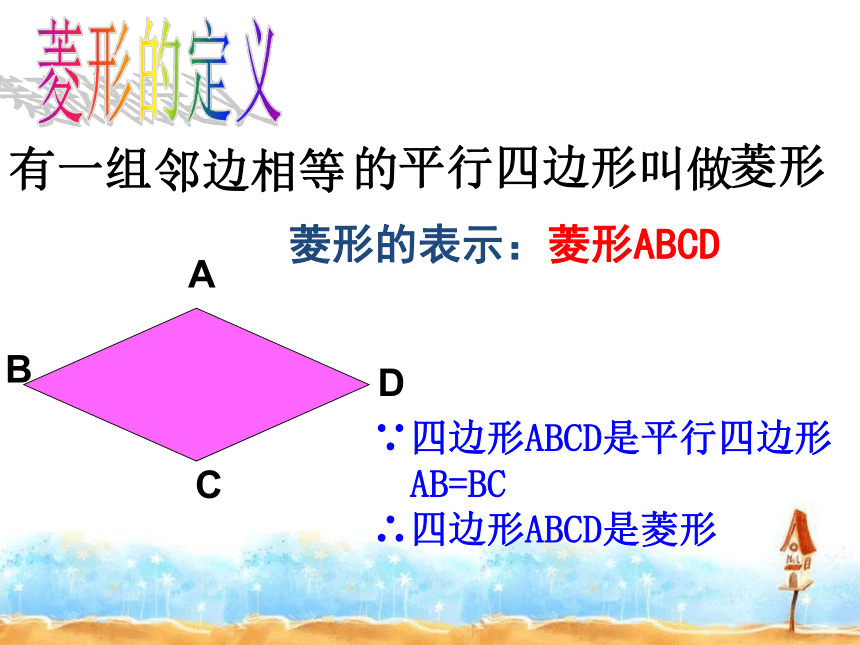
分别平行矩形情景创设 前面我们学习了平行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?有一个角是直角菱形(矩形,由角变化得到) 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度,让它有一组邻边相等,这个特殊的四边形叫什么呢?有一组邻边相等菱形菱形的定义有一组 的 叫做邻边相等 平行四边形 ADCB菱形 ∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形菱形的表示:菱形ABCD感受生活你能举出生活中你看到的菱形吗?菱形就在我们身边三菱汽车标志欣赏感受生活创设情境 引出课题对边平行且相等 对角相等 对角线互相平分 对角线把平行四边
形分成四个面积相
等的三角形 对边平行且相等 四个角都是直角 对角线互相平分且相等 对角线把矩形分成四个面积相等的等腰三角形菱形的性质:包括一般性质和特殊性质提示:从边、角、对角线、面积等方面来探讨
几何画板演示 猜想1:菱形的四条边都相等。猜想2:菱形的两条对角线互相垂直,每一条对角线平分一组对角。问题:菱形是特殊的平行四边形,因此它具有平行四边形的所有性质.类似于矩形,菱形是否也具有一般平行四边形不具有的特殊性质?如果有,是什么?已知:如图四边形ABCD是菱形求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。证明:(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC∴AB=BC=DC=DA(2)在△DAC中,∵ DA=DC ,AO=CO∴DB⊥AC,DB平分∠ADC(三线合一)同理: DB平分∠ABC;AC平分∠DAB和∠DCB(1)AB=BC=CD=DA (2)AC⊥BD AC平分∠DAB和∠DCB, BD平分∠ADC和∠ABC 求证:菱形的 两条对角线互相平分菱形的两组对边平行边对角线角菱形的性质菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直平,每一条对角线平分一组对角。练一练3cm600C练一练4.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。课本P57练习15、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积生活中的数学相邻两角的度数比为1:2生活中的数学菱形的面积公式6.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2=8(1)性质对比 问题5 现在,我们得到了菱形的性质.如果把矩形
和菱形的性质进行比较,发现它们很相似.你能写出矩
形、菱形的定义及它们的特殊性质并进行比较吗?矩形和菱形特殊性质比较 相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:菱形ABCD中AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线”小结:矩形和菱形的性质学而时习之,不亦说乎?1.课本P57练习2,P60第5题,
P61第11题
2.练习册P43
3.预习P57-58如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。你敢挑战吗?回去想一想∵四边形ABCD是平行四边形 ∴∠DAB+∠ABC=180 °证明一:同理:∠EFG=90°,∠FGH=90°∴四边形EFGH是矩形∵AE、BE分别平分∠DAB、∠ABC ∴∠EAB+∠EBA=90 °即∠AEB=90° ∴∠HEF=90°证明二:∵四边形ABCD是平行四边形
∴∠ABC=∠ADC又∵AN、DM是∠ABC、∠ADC的平分线∴∠ABQ=∠QBC=∠ADM=∠CDM又∵AD∥BC ∴ ∠ AQB =∠ QBC = ∠ ADM∴BQ∥DM∵AE、BE分别平分∠DAB、∠ABC ∴∠EAB+∠EBA=90 °即∠AEB=90° ∴∠HEF=90°∴四边形EFGH是矩形同理:AN∥CP ∴四边形EFGH是平行四边形课后作业 1.课本P55练习2,练习册P42第9题
2.练习册P42第8题,中考真题1,2
3.预习P57-58
补充:
如图,四边形ABCD中,DE=BF,AC、EF互相平分于点O,∠B=90°,求证:四边形ABCD是矩形。ABCDEFO
求证 : 四边形ABCD是矩形。证明:
∵AB=6,BC=8,AC=10
∴AB2+BC2=62+82=100=102=AC2
∴ ∠B=90°
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形3.已知矩形ABCD的对角线AC、BD相交于O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH。
求证:四边形EFGH是矩形。证明: ∵四边形ABCD是矩形∴ AO=BO=CO=DO又∵ AE=BF=CG=DH∴OE=OF=OG=OH∴四边形EFGH是平行四边形又∵EO+OG=FO+OH即EG=FH∴四边形EFGH是矩形例1.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,且OA=OD, ∠OAD= 50° ,求∠OAB 的度数。解: ∵四边形ABCD是平行四边形∴ OA=OC=1/2AC,OB=OD=1/2BD 又 OA=OD∴ AC=BD∴四边形ABCD是矩形∴ ∠DAB= 90°又∠0AD= 50°∴ ∠0AB= 40°4.已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是______;
(2)试用理由说明你的猜想.相等且互相平分18.2.2菱形(1) 学习目标:
1.理解菱形的概念;
2.会用菱形的性质解决简单的问题;
3.经历类比矩形探究菱形性质的过程,通过观察、类比、猜想、证明,体会几何图形探究的一般步骤和方法;
学习重难点:
重点:菱形性质的探索、证明与应用两组对边
分别平行矩形情景创设 前面我们学习了平行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?有一个角是直角菱形(矩形,由角变化得到) 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度,让它有一组邻边相等,这个特殊的四边形叫什么呢?有一组邻边相等菱形菱形的定义有一组 的 叫做邻边相等 平行四边形 ADCB菱形 ∵四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形菱形的表示:菱形ABCD感受生活你能举出生活中你看到的菱形吗?菱形就在我们身边三菱汽车标志欣赏感受生活创设情境 引出课题对边平行且相等 对角相等 对角线互相平分 对角线把平行四边
形分成四个面积相
等的三角形 对边平行且相等 四个角都是直角 对角线互相平分且相等 对角线把矩形分成四个面积相等的等腰三角形菱形的性质:包括一般性质和特殊性质提示:从边、角、对角线、面积等方面来探讨
几何画板演示 猜想1:菱形的四条边都相等。猜想2:菱形的两条对角线互相垂直,每一条对角线平分一组对角。问题:菱形是特殊的平行四边形,因此它具有平行四边形的所有性质.类似于矩形,菱形是否也具有一般平行四边形不具有的特殊性质?如果有,是什么?已知:如图四边形ABCD是菱形求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。证明:(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC∴AB=BC=DC=DA(2)在△DAC中,∵ DA=DC ,AO=CO∴DB⊥AC,DB平分∠ADC(三线合一)同理: DB平分∠ABC;AC平分∠DAB和∠DCB(1)AB=BC=CD=DA (2)AC⊥BD AC平分∠DAB和∠DCB, BD平分∠ADC和∠ABC 求证:菱形的 两条对角线互相平分菱形的两组对边平行边对角线角菱形的性质菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直平,每一条对角线平分一组对角。练一练3cm600C练一练4.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。课本P57练习15、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积生活中的数学相邻两角的度数比为1:2生活中的数学菱形的面积公式6.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。2∵四边形ABCD是菱形, ∴AD=AB解:∴AD=AB=BD∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)∴ ∠DAB= 60 °, ∴ ∠ABC=120 °(2)∵AE=2, ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4(3)在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2=8(1)性质对比 问题5 现在,我们得到了菱形的性质.如果把矩形
和菱形的性质进行比较,发现它们很相似.你能写出矩
形、菱形的定义及它们的特殊性质并进行比较吗?矩形和菱形特殊性质比较 相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:菱形ABCD中AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678知识再现1个定义2个公式3个特性:有一组邻边相等的平行四边形叫菱形:S菱形=底×高
S菱形= 对角线乘积的一半:特在“边、对角线”小结:矩形和菱形的性质学而时习之,不亦说乎?1.课本P57练习2,P60第5题,
P61第11题
2.练习册P43
3.预习P57-58如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。你敢挑战吗?回去想一想∵四边形ABCD是平行四边形 ∴∠DAB+∠ABC=180 °证明一:同理:∠EFG=90°,∠FGH=90°∴四边形EFGH是矩形∵AE、BE分别平分∠DAB、∠ABC ∴∠EAB+∠EBA=90 °即∠AEB=90° ∴∠HEF=90°证明二:∵四边形ABCD是平行四边形
∴∠ABC=∠ADC又∵AN、DM是∠ABC、∠ADC的平分线∴∠ABQ=∠QBC=∠ADM=∠CDM又∵AD∥BC ∴ ∠ AQB =∠ QBC = ∠ ADM∴BQ∥DM∵AE、BE分别平分∠DAB、∠ABC ∴∠EAB+∠EBA=90 °即∠AEB=90° ∴∠HEF=90°∴四边形EFGH是矩形同理:AN∥CP ∴四边形EFGH是平行四边形课后作业 1.课本P55练习2,练习册P42第9题
2.练习册P42第8题,中考真题1,2
3.预习P57-58
补充:
如图,四边形ABCD中,DE=BF,AC、EF互相平分于点O,∠B=90°,求证:四边形ABCD是矩形。ABCDEFO
