1.4 解直角三角形 课件(共24张PPT)-2023-2024学年九年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 1.4 解直角三角形 课件(共24张PPT)-2023-2024学年九年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 659.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 06:03:00 | ||
图片预览








文档简介
北师大版 数学 九年级下册
第一章 直角三角形的边角关系
4 解直角三角形
学习目标
1.了解解直角三角形的概念,明确解直角三角形除了直角外至少需要两个条件(其中至少一个是边),能用锐角三角函数解直角三角形.(重点)
2.经历解直角三角形的过程,掌握运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形的方法.(难点)
(1)三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:
sinA=_____,cosA=_____,tanA=_____.
A
C
B
c
b
a
如图,在Rt△ABC中,其中∠C=90°。它的边、角以及边角之间都有什么关系呢?
复习回顾
c2
90°
勾股定理
????????
?
????????
?
????????
?
直角三角形两锐角互余
锐角三角函数
生活中,我们常常遇到与直角三角形有关的问题.为了解决这些问题,往往需要确定直角三角形的边和角.
直角三角形中除了直角外,还有5个元素,分别是三条边和2个角.那么至少知道几个元素就可以求出其他的元素呢?
A
C
B
一、创设情境,引入新知
利用边、角以及边角之间的关系,至少知道其中的两个元素(至少有一个是边)后,就可求出其余的元素.
A
B
C
例1:在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且????=????????,????=????,求这个直角三角形的其他元素.
?
典型例题
二、自主合作,探究新知
探究一:已知两边解直角三角形
做一做:在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他的元素吗?
分析:直角三角形中已知两边可以利用 求出第三条边;
直角三角形中,已知两边可以利用 求∠A(或∠B)的度数;
再利用 求∠B(或∠A)的度数.
勾股定理
锐角三角函数
两锐角互余
二、自主合作,探究新知
解:在Rt△ABC中,a2+b2=c2,a=????????,b=????,
∴????=????????+????????=(????????)????+(????)????=????????.
在Rt△ABC中,sin B=????????=????????????=????????,
∴ ∠B=30°
∴ ∠A=90°-∠B=60°.
?
A
B
C
想一想:还有没有其他解题思路呢?
二、自主合作,探究新知
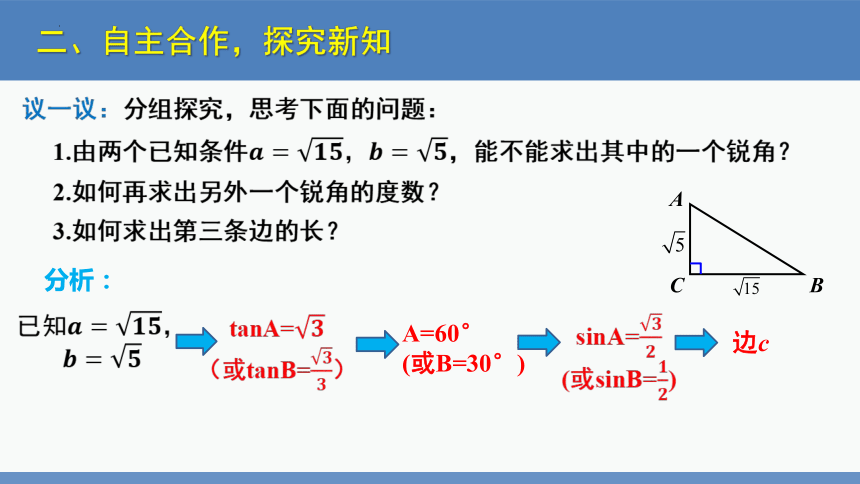
议一议:分组探究,思考下面的问题:
1.由两个已知条件????=????????,????=????,能不能求出其中的一个锐角?
2.如何再求出另外一个锐角的度数?
3.如何求出第三条边的长?
?
A
B
C
tanA=????
(或tanB=????????)
?
A=60°
(或B=30°)
sinA=????????
(或sinB=????????)
?
边c
分析:
已知????=????????,
????=????
?
二、自主合作,探究新知
解:在Rt△ABC中,a=????????,b=????,
∴tanA=????????=????????????=????.
∴∠A=60°,∠B=90°-∠A=30°
在Rt△ABC中,sin A=????????=????????????=????????,
∴ ????=????????.
?
A
B
C
方法二:
知识要点
二、自主合作,探究新知
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
已知直角三角形两条边求其他元素的方法:
方法1:已知两条边的长度,可以先利用勾股定理求出第三条边,然后利用锐角三角函数求出其中一个锐角,再根据直角三角形两锐角互余求出另外一个锐角.
方法2:已知两条边的长度,可以先利用锐角三角函数求出其中一个锐角,然后根据直角三角形中两锐角互余求出另外一个锐角,再利用锐角三角函数求出第三条边.
二、自主合作,探究新知
探究二:已知一边和一个锐角解直角三角形
想一想:在Rt△ABC中,如果已知一边和一个锐角,你能求出这个三角形的其他元素吗?
例2:如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a, b, c,且b=30,∠B=25°,求这个直角三角形的其他元素(边长精确到1).
A
B
C
b
30
c
a
25°
典型例题
分析:直角三角形中已知一边和一个锐角,可以利用 求∠A的度数.再利用 求出另两条边.
锐角三角函数
两锐角互余
二、自主合作,探究新知
解:
在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=90°-∠B=65°.
A
B
C
b
30
c
a
25°
也可以利用勾股定理求出第三条边.
二、自主合作,探究新知
已知直角三角形一条边和一个锐角求其他元素的方法:
已知一个锐角,先根据直角三角形两锐角互余求出另外一个锐角.
知道一条边的长,根据三角函数的定义可以求出另外两条边的长;
也可以先利用三角函数的定义求出其中一条边的长,再利用勾股定理求出第三条边的长.
知识要点
二、自主合作,探究新知
议一议:(1)除了已知“两边”和“一边一角”解直角三角形外,还有其他的情况解直角三角形吗?
(2)在Rt△ABC中,如果已知两个锐角,可以解直角三角形吗?先独立判断,再分组讨论.
只知道角度是无法求出直角三角形的边长的.
(3)只给出一条边长这一个条件,可以解直角三角形吗?
不能.
二、自主合作,探究新知
知识要点
解直角三角形需要满足的条件:
在直角三角形的6个元素中,直角是已知元素,如果再知道一条边和第三个元素,那么这个三角形的所有元素就都可以确定下来.
A
B
a
b
c
C
注意:解直角三角形必须满足的一个条件是已知“一条边”.
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,
AB=8,则BC的长是( )
三、即学即练,应用知识
2.在Rt△ABC中,已知∠C=90°,∠A=50°,BC=3,则AC=( )A.3sin 50° B.3sin 40° C.3tan 50° D.3tan 40°
D
D
3.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB=????????,则AC的长为( )
A.3 B.3.75 C.4.8 D.5
?
5.在△ABC中,∠B=60°,∠C=45°,AB=2????,则AC=________.
?
三、即学即练,应用知识
3????
?
B
4.在△ABC中,AB=AC=3,BC=4,则cosB 的值是_________.
三、即学即练,应用知识
6.在Rt△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,已知c=10,∠B=30°,解这个直角三角形.
解:∵在Rt△ABC中,∠C为直角,∠B=30°,
∴∠A=90°-∠B=90°-30°=60°.
∵cos B=????????,
∴a=c·cos B=10·cos 30°=10×????????=5????.
∵sin B=????????,
∴b=c·sin B=10·sin 30°=10×????????=5.
?
30°
10
7.在Rt△ABC中,已知∠C=90°,a = 30 , b = 20 ,解这个直角三角形.
A
B
C
b=20
a=30
c
三、即学即练,应用知识
解:根据勾股定理得
四、课堂小结
解直角三角形
依据
勾股定理
直角三角形两锐角互余
锐角三角函数
定义:由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
类型
已知直角三角形的两边;
已知直角三角形一边和一个锐角.
1.在Rt△ABC中,已知∠C=90°,∠A=30°,AC=2????,则BC=( )
A.2???? B.2 C.4 D.6
?
五、当堂达标检测
B
2.如图,小明为了测量其所在位置点A到河对岸点B之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )米.
A.m·sin α B.m·tan α
C.m·cos α D. ????????????????????
?
B
4.在△ABC中,已知AB=3????,AC=6,∠B=45°,则BC= .
?
五、当堂达标检测
3.在Rt△ABC中,已知∠C=90°,AC=1,BC=????,则cosA= .
?
????????
?
????????+????或?????????????
?
5. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线????????=????????,解这个直角三角形.
?
D
A
B
C
6
五、当堂达标检测
解:
∵AD平分∠BAC,
五、当堂达标检测
6.在Rt△ABC中,已知∠C=90°,∠B=72°,c = 14,解这个直角三角形.
A
B
C
b
a
c=14
解:
∴????=?????????????????????=????????×????????????????????°≈????.????
?
∴????=?????????????????????=????????×????????????????????°≈????????.????
?
教材习题1.5.
六、布置作业
第一章 直角三角形的边角关系
4 解直角三角形
学习目标
1.了解解直角三角形的概念,明确解直角三角形除了直角外至少需要两个条件(其中至少一个是边),能用锐角三角函数解直角三角形.(重点)
2.经历解直角三角形的过程,掌握运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形的方法.(难点)
(1)三边之间的关系:a2+b2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:
sinA=_____,cosA=_____,tanA=_____.
A
C
B
c
b
a
如图,在Rt△ABC中,其中∠C=90°。它的边、角以及边角之间都有什么关系呢?
复习回顾
c2
90°
勾股定理
????????
?
????????
?
????????
?
直角三角形两锐角互余
锐角三角函数
生活中,我们常常遇到与直角三角形有关的问题.为了解决这些问题,往往需要确定直角三角形的边和角.
直角三角形中除了直角外,还有5个元素,分别是三条边和2个角.那么至少知道几个元素就可以求出其他的元素呢?
A
C
B
一、创设情境,引入新知
利用边、角以及边角之间的关系,至少知道其中的两个元素(至少有一个是边)后,就可求出其余的元素.
A
B
C
例1:在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且????=????????,????=????,求这个直角三角形的其他元素.
?
典型例题
二、自主合作,探究新知
探究一:已知两边解直角三角形
做一做:在Rt△ABC中,如果已知其中两边的长,你能求出这个三角形的其他的元素吗?
分析:直角三角形中已知两边可以利用 求出第三条边;
直角三角形中,已知两边可以利用 求∠A(或∠B)的度数;
再利用 求∠B(或∠A)的度数.
勾股定理
锐角三角函数
两锐角互余
二、自主合作,探究新知
解:在Rt△ABC中,a2+b2=c2,a=????????,b=????,
∴????=????????+????????=(????????)????+(????)????=????????.
在Rt△ABC中,sin B=????????=????????????=????????,
∴ ∠B=30°
∴ ∠A=90°-∠B=60°.
?
A
B
C
想一想:还有没有其他解题思路呢?
二、自主合作,探究新知
议一议:分组探究,思考下面的问题:
1.由两个已知条件????=????????,????=????,能不能求出其中的一个锐角?
2.如何再求出另外一个锐角的度数?
3.如何求出第三条边的长?
?
A
B
C
tanA=????
(或tanB=????????)
?
A=60°
(或B=30°)
sinA=????????
(或sinB=????????)
?
边c
分析:
已知????=????????,
????=????
?
二、自主合作,探究新知
解:在Rt△ABC中,a=????????,b=????,
∴tanA=????????=????????????=????.
∴∠A=60°,∠B=90°-∠A=30°
在Rt△ABC中,sin A=????????=????????????=????????,
∴ ????=????????.
?
A
B
C
方法二:
知识要点
二、自主合作,探究新知
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
已知直角三角形两条边求其他元素的方法:
方法1:已知两条边的长度,可以先利用勾股定理求出第三条边,然后利用锐角三角函数求出其中一个锐角,再根据直角三角形两锐角互余求出另外一个锐角.
方法2:已知两条边的长度,可以先利用锐角三角函数求出其中一个锐角,然后根据直角三角形中两锐角互余求出另外一个锐角,再利用锐角三角函数求出第三条边.
二、自主合作,探究新知
探究二:已知一边和一个锐角解直角三角形
想一想:在Rt△ABC中,如果已知一边和一个锐角,你能求出这个三角形的其他元素吗?
例2:如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a, b, c,且b=30,∠B=25°,求这个直角三角形的其他元素(边长精确到1).
A
B
C
b
30
c
a
25°
典型例题
分析:直角三角形中已知一边和一个锐角,可以利用 求∠A的度数.再利用 求出另两条边.
锐角三角函数
两锐角互余
二、自主合作,探究新知
解:
在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=90°-∠B=65°.
A
B
C
b
30
c
a
25°
也可以利用勾股定理求出第三条边.
二、自主合作,探究新知
已知直角三角形一条边和一个锐角求其他元素的方法:
已知一个锐角,先根据直角三角形两锐角互余求出另外一个锐角.
知道一条边的长,根据三角函数的定义可以求出另外两条边的长;
也可以先利用三角函数的定义求出其中一条边的长,再利用勾股定理求出第三条边的长.
知识要点
二、自主合作,探究新知
议一议:(1)除了已知“两边”和“一边一角”解直角三角形外,还有其他的情况解直角三角形吗?
(2)在Rt△ABC中,如果已知两个锐角,可以解直角三角形吗?先独立判断,再分组讨论.
只知道角度是无法求出直角三角形的边长的.
(3)只给出一条边长这一个条件,可以解直角三角形吗?
不能.
二、自主合作,探究新知
知识要点
解直角三角形需要满足的条件:
在直角三角形的6个元素中,直角是已知元素,如果再知道一条边和第三个元素,那么这个三角形的所有元素就都可以确定下来.
A
B
a
b
c
C
注意:解直角三角形必须满足的一个条件是已知“一条边”.
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,
AB=8,则BC的长是( )
三、即学即练,应用知识
2.在Rt△ABC中,已知∠C=90°,∠A=50°,BC=3,则AC=( )A.3sin 50° B.3sin 40° C.3tan 50° D.3tan 40°
D
D
3.如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB=????????,则AC的长为( )
A.3 B.3.75 C.4.8 D.5
?
5.在△ABC中,∠B=60°,∠C=45°,AB=2????,则AC=________.
?
三、即学即练,应用知识
3????
?
B
4.在△ABC中,AB=AC=3,BC=4,则cosB 的值是_________.
三、即学即练,应用知识
6.在Rt△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,已知c=10,∠B=30°,解这个直角三角形.
解:∵在Rt△ABC中,∠C为直角,∠B=30°,
∴∠A=90°-∠B=90°-30°=60°.
∵cos B=????????,
∴a=c·cos B=10·cos 30°=10×????????=5????.
∵sin B=????????,
∴b=c·sin B=10·sin 30°=10×????????=5.
?
30°
10
7.在Rt△ABC中,已知∠C=90°,a = 30 , b = 20 ,解这个直角三角形.
A
B
C
b=20
a=30
c
三、即学即练,应用知识
解:根据勾股定理得
四、课堂小结
解直角三角形
依据
勾股定理
直角三角形两锐角互余
锐角三角函数
定义:由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
类型
已知直角三角形的两边;
已知直角三角形一边和一个锐角.
1.在Rt△ABC中,已知∠C=90°,∠A=30°,AC=2????,则BC=( )
A.2???? B.2 C.4 D.6
?
五、当堂达标检测
B
2.如图,小明为了测量其所在位置点A到河对岸点B之间的距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,那么AB等于( )米.
A.m·sin α B.m·tan α
C.m·cos α D. ????????????????????
?
B
4.在△ABC中,已知AB=3????,AC=6,∠B=45°,则BC= .
?
五、当堂达标检测
3.在Rt△ABC中,已知∠C=90°,AC=1,BC=????,则cosA= .
?
????????
?
????????+????或?????????????
?
5. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线????????=????????,解这个直角三角形.
?
D
A
B
C
6
五、当堂达标检测
解:
∵AD平分∠BAC,
五、当堂达标检测
6.在Rt△ABC中,已知∠C=90°,∠B=72°,c = 14,解这个直角三角形.
A
B
C
b
a
c=14
解:
∴????=?????????????????????=????????×????????????????????°≈????.????
?
∴????=?????????????????????=????????×????????????????????°≈????????.????
?
教材习题1.5.
六、布置作业
