4.2 立体图形的视图 课件(共32张PPT)-2023-2024学年七年级数学上册同步精品课堂(华东师大版)
文档属性
| 名称 | 4.2 立体图形的视图 课件(共32张PPT)-2023-2024学年七年级数学上册同步精品课堂(华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 06:07:18 | ||
图片预览






文档简介
(共32张PPT)
4.2 立体图形的视图
数学(华东师大版)
七年级 上册
第4章 图形的初步认识
学习目标
1、能识别简单物体从三个方向看到的形状图;
2、会画立体图形的三视图;
3、进一步识别物体从三个方向看到的形状图;
4、能根据三种视图描述基本几何体或实物原形.
导入新课
工人在建选房子之前,首先要看房子的图纸.但在平面上画空间的物体不是一件简单的事,因为必须把它画得从各个角度都能看得很清楚.
为了解决这个问题,可以采用三视图法.
导入新课
视图来自投影.
窗框的影子
皮影
人和骆驼的影子
手影
讲授新课
知识点一 三视图
视图来自于投影.投影现象广泛存在于我们日常生活中,根据光源发出的光线不同,有中心投影和平行投影,如:灯光的光线可以看作是从一点发出的,我们称这种投影为中心投影;太阳的光线可以看是平行的,我们称这种投影为平行投影;视图是一种特殊的平行投影.
中心投影
平行投影
讲授新课
正面
侧面
水平面
主视图
俯视图
左视图
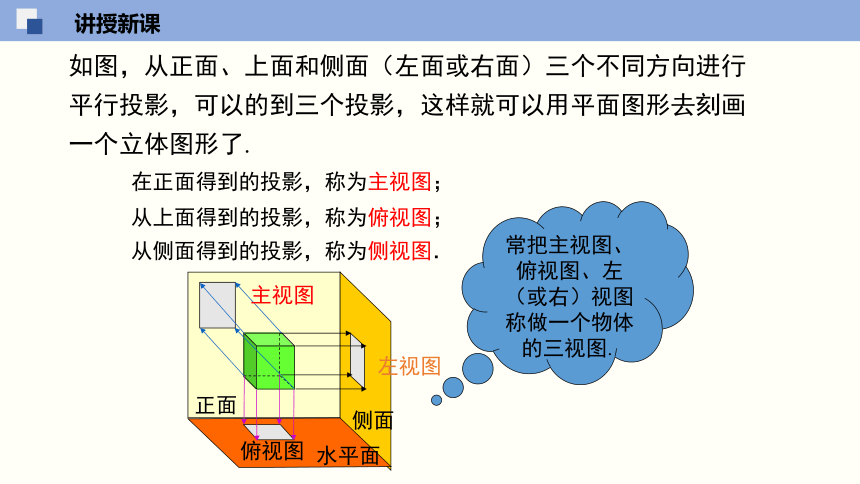
如图,从正面、上面和侧面(左面或右面)三个不同方向进行平行投影,可以的到三个投影,这样就可以用平面图形去刻画一个立体图形了.
从上面得到的投影,称为俯视图;
从侧面得到的投影,称为侧视图.
在正面得到的投影,称为主视图;
常把主视图、俯视图、左(或右)视图称做一个物体的三视图.
讲授新课
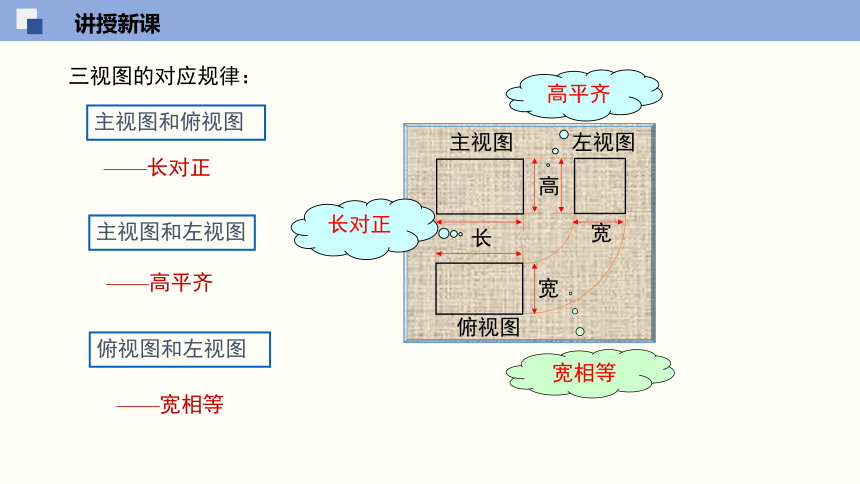
三视图的对应规律:
俯视图和左视图
主视图和俯视图
主视图和左视图
——长对正
——高平齐
——宽相等
主视图
俯视图
左视图
高
长
宽
宽
高平齐
长对正
宽相等
讲授新课
主视图
左视图
俯视图
在画三种视图时,对应部分的长度要相等.
长
宽
高
长对正、高平齐、宽相等
通常把俯视图画在主视图下面,把左视图画在主视图右面.
讲授新课
主 视 图
左 视 图
俯 视 图
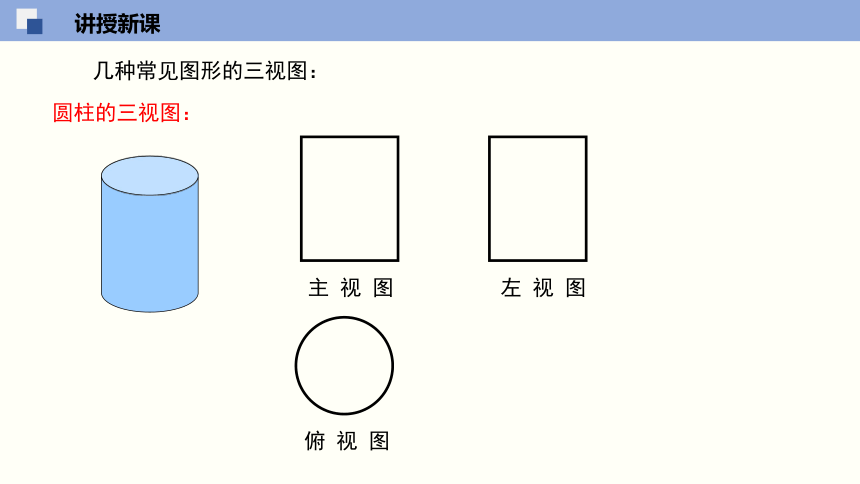
圆柱的三视图:
几种常见图形的三视图:
讲授新课
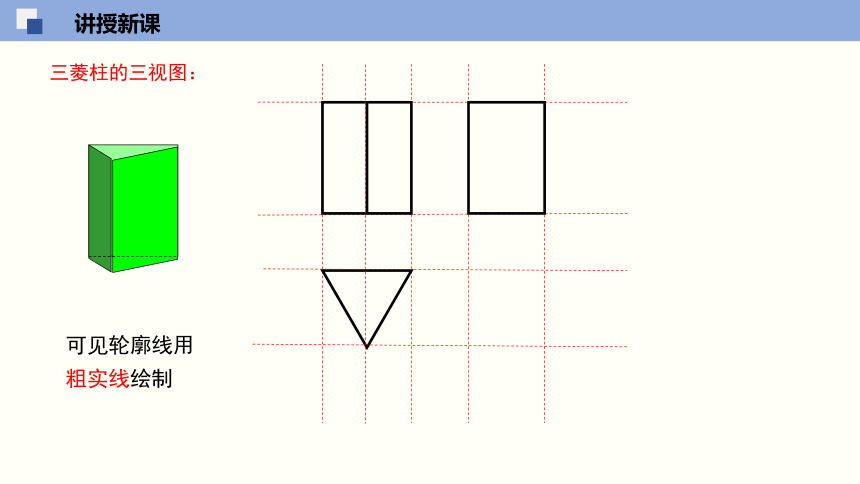
可见轮廓线用粗实线绘制
三菱柱的三视图:
讲授新课
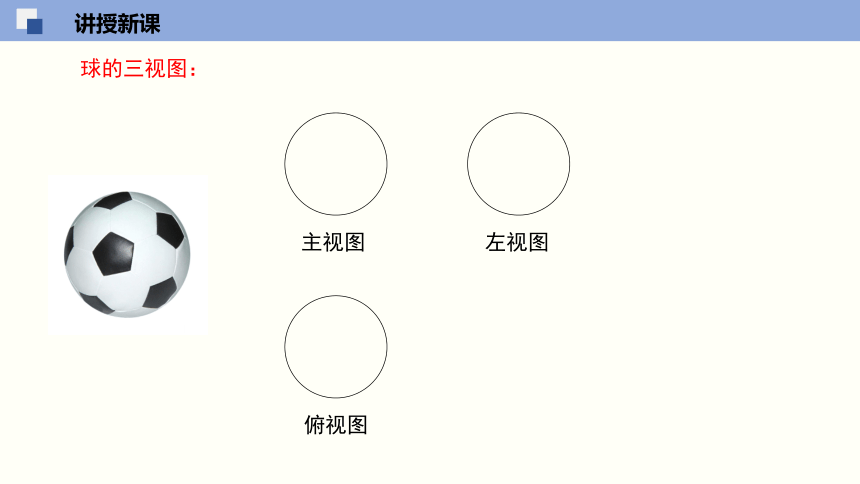
主视图
左视图
俯视图
球的三视图:
讲授新课
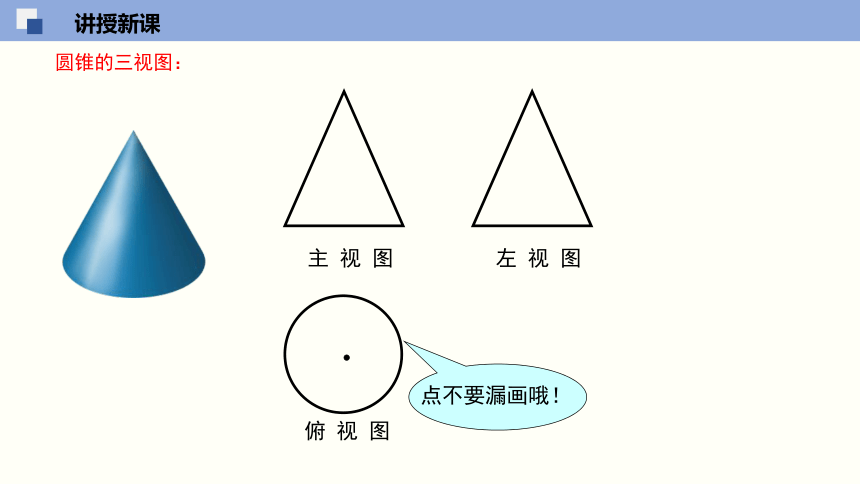
俯 视 图
左 视 图
主 视 图
点不要漏画哦!
圆锥的三视图:
讲授新课
典例精析
【例1】画出如图1和图2所示的正方体和圆柱的三视图.
图1
图2
讲授新课
图1
主视图
左视图
俯视图
正方体的三视图都是正方形
讲授新课
图2
主视图
左视图
俯视图
圆柱的主视图和左视图都是长方形,俯视图是圆.
讲授新课
练一练
1、画出如图所示的圆锥的三视图.
主视图
左视图
俯视图
讲授新课
2、画出图所示的支架(一 种小零件)的三视图.
分析:支架的现状:由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长方体的上下、前后位置关系.
解:图是支架的三视图.
主视图
俯视图
左视图
讲授新课
知识点二 由视图到立体图形
【例2】根据三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1) 从三个方向看立体图形,图象都是矩形,可以想象出:整体是长方体,如图所示.
主视图
俯视图
左视图
(1)
讲授新课
解:(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图象是圆;可以想象出:整体是圆锥,如图所示.
(2)
主视图
俯视图
左视图
讲授新课
练一练
1、根据物体的三视图摸索物体的形状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图 可知,物体的侧面是矩形的,且有一条棱(中间的实线)可见到.综合各视图可知,物体是五棱柱形状的.
解:物体是五棱柱形状的,如图所示.
主视图
俯视图
左视图
讲授新课
由三视图想象实物的形状:
实物
实物
讲授新课
实物
实物
讲授新课
根据三视图描述物体的形状.
主视图
俯视图
左视图
实物形状
当堂检测
1.找出图中每一物品所对应的主视图.
A
B
C
D
当堂检测
2.下图是一根钢管的直观图,画出它的三视图.
解:下图是钢管的三视图,其中的虚线表示钢管的内壁.
主视图
俯视图
左视图
当堂检测
3、图中右边是由四个相同的小长方体堆成的物体,试指出左边三个平面图形分别是这个物体的三视图中的哪个视图.
( )
( )
( )
主视图
俯视图
左视图
当堂检测
4、用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
正确
错误
当堂检测
5.如图所示的几何体由8个相同的小正方体组成,请你画出分别从正面、左面、上面看这个几何体时看到的图形.
解:画出的图形如答图所示.
当堂检测
6.用正方体搭成的一个物体,从上面看和正面看到的图形如下图,搭成这个物体所需的小正方体个数最少是多少?最多是多少?
答案:最少是6个,最多是7个
当堂检测
7、下图是一个立体图形从三个方向看到的图形,请写出这个立体图形的名称,并计算这个立体图形的体积(结果保留π).
解:该立体图形为圆柱.
∵圆柱的底面半径r=5,
高h=10,
∴圆柱的体积V=πr2h
=π×52×10=250π.
答:立体图形的体积为250π.
课堂小结
三视图
立体图形的视图
从正面看
从左面看
从上面看
由视图到立体图形
根据从前面看到的图形、从上面看到的图形和从左边看到的图形想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形.
谢 谢~
4.2 立体图形的视图
数学(华东师大版)
七年级 上册
第4章 图形的初步认识
学习目标
1、能识别简单物体从三个方向看到的形状图;
2、会画立体图形的三视图;
3、进一步识别物体从三个方向看到的形状图;
4、能根据三种视图描述基本几何体或实物原形.
导入新课
工人在建选房子之前,首先要看房子的图纸.但在平面上画空间的物体不是一件简单的事,因为必须把它画得从各个角度都能看得很清楚.
为了解决这个问题,可以采用三视图法.
导入新课
视图来自投影.
窗框的影子
皮影
人和骆驼的影子
手影
讲授新课
知识点一 三视图
视图来自于投影.投影现象广泛存在于我们日常生活中,根据光源发出的光线不同,有中心投影和平行投影,如:灯光的光线可以看作是从一点发出的,我们称这种投影为中心投影;太阳的光线可以看是平行的,我们称这种投影为平行投影;视图是一种特殊的平行投影.
中心投影
平行投影
讲授新课
正面
侧面
水平面
主视图
俯视图
左视图
如图,从正面、上面和侧面(左面或右面)三个不同方向进行平行投影,可以的到三个投影,这样就可以用平面图形去刻画一个立体图形了.
从上面得到的投影,称为俯视图;
从侧面得到的投影,称为侧视图.
在正面得到的投影,称为主视图;
常把主视图、俯视图、左(或右)视图称做一个物体的三视图.
讲授新课
三视图的对应规律:
俯视图和左视图
主视图和俯视图
主视图和左视图
——长对正
——高平齐
——宽相等
主视图
俯视图
左视图
高
长
宽
宽
高平齐
长对正
宽相等
讲授新课
主视图
左视图
俯视图
在画三种视图时,对应部分的长度要相等.
长
宽
高
长对正、高平齐、宽相等
通常把俯视图画在主视图下面,把左视图画在主视图右面.
讲授新课
主 视 图
左 视 图
俯 视 图
圆柱的三视图:
几种常见图形的三视图:
讲授新课
可见轮廓线用粗实线绘制
三菱柱的三视图:
讲授新课
主视图
左视图
俯视图
球的三视图:
讲授新课
俯 视 图
左 视 图
主 视 图
点不要漏画哦!
圆锥的三视图:
讲授新课
典例精析
【例1】画出如图1和图2所示的正方体和圆柱的三视图.
图1
图2
讲授新课
图1
主视图
左视图
俯视图
正方体的三视图都是正方形
讲授新课
图2
主视图
左视图
俯视图
圆柱的主视图和左视图都是长方形,俯视图是圆.
讲授新课
练一练
1、画出如图所示的圆锥的三视图.
主视图
左视图
俯视图
讲授新课
2、画出图所示的支架(一 种小零件)的三视图.
分析:支架的现状:由两个大小不等的长方体构成的组合体,画三视图时要注意这两个长方体的上下、前后位置关系.
解:图是支架的三视图.
主视图
俯视图
左视图
讲授新课
知识点二 由视图到立体图形
【例2】根据三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1) 从三个方向看立体图形,图象都是矩形,可以想象出:整体是长方体,如图所示.
主视图
俯视图
左视图
(1)
讲授新课
解:(2)从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图象是圆;可以想象出:整体是圆锥,如图所示.
(2)
主视图
俯视图
左视图
讲授新课
练一练
1、根据物体的三视图摸索物体的形状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向下看物体是矩形的,且有一条棱(中间的实线)可见到,两条棱(虚线)被遮挡;由左视图 可知,物体的侧面是矩形的,且有一条棱(中间的实线)可见到.综合各视图可知,物体是五棱柱形状的.
解:物体是五棱柱形状的,如图所示.
主视图
俯视图
左视图
讲授新课
由三视图想象实物的形状:
实物
实物
讲授新课
实物
实物
讲授新课
根据三视图描述物体的形状.
主视图
俯视图
左视图
实物形状
当堂检测
1.找出图中每一物品所对应的主视图.
A
B
C
D
当堂检测
2.下图是一根钢管的直观图,画出它的三视图.
解:下图是钢管的三视图,其中的虚线表示钢管的内壁.
主视图
俯视图
左视图
当堂检测
3、图中右边是由四个相同的小长方体堆成的物体,试指出左边三个平面图形分别是这个物体的三视图中的哪个视图.
( )
( )
( )
主视图
俯视图
左视图
当堂检测
4、用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
正确
错误
当堂检测
5.如图所示的几何体由8个相同的小正方体组成,请你画出分别从正面、左面、上面看这个几何体时看到的图形.
解:画出的图形如答图所示.
当堂检测
6.用正方体搭成的一个物体,从上面看和正面看到的图形如下图,搭成这个物体所需的小正方体个数最少是多少?最多是多少?
答案:最少是6个,最多是7个
当堂检测
7、下图是一个立体图形从三个方向看到的图形,请写出这个立体图形的名称,并计算这个立体图形的体积(结果保留π).
解:该立体图形为圆柱.
∵圆柱的底面半径r=5,
高h=10,
∴圆柱的体积V=πr2h
=π×52×10=250π.
答:立体图形的体积为250π.
课堂小结
三视图
立体图形的视图
从正面看
从左面看
从上面看
由视图到立体图形
根据从前面看到的图形、从上面看到的图形和从左边看到的图形想象立体图形的前面、上面和左侧面的局部形状,然后再综合起来考虑整体图形.
谢 谢~
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
