第二十七章 相似 章末总结 课件(共62张PPT)-九年级数学下册同步备课系列(人教版)
文档属性
| 名称 | 第二十七章 相似 章末总结 课件(共62张PPT)-九年级数学下册同步备课系列(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 06:24:00 | ||
图片预览








文档简介
(共62张PPT)
相似
章节总结
第二十七章
学习目标
1.加深了解比例的基本性质、线段的比、成比例线段,认识图形的相似、位似等概念和性质;
2.理解相似图形的性质与判定、位似的性质与把一个图形放大或缩小,在同一坐标系下感受位似变换后点的坐标的变化规律.
中学阶段重点研究的两个平面图形间的关系是全等和相似,全等是一种特殊的相似.本章将在前面对全等形研究的基础上,借鉴全等三角形研究的基本套路对相似图形进行研究.本章研究的主要问题是相似图形的定义、性质和判定方法,研究的主要载体是三角形.此外,教科书在前面的章节中介绍了平移、轴对称和旋转三种图形的全等变换,本章将介绍一种新的图形变换-位似.
基础巩固(相似多边形相关概念)
相似多边形概念:
相似多边形的特征:
如果两个边数相同的多边形对应角相等、对应边成比例的两个多边形叫做相似多边形.
相似多边形的对应角相等、对应边成比例.
相似比概念:
相似多边形对应边的比叫做相似比.
相似多边形的表示:
相似多边形用符号“∽”表示,读作“相似于”.
【注意】在记两个相似多边形时,要把表示对应顶点的字母写在对应的位置上.
基础巩固(比例线段)
比例线段的概念:
对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段.
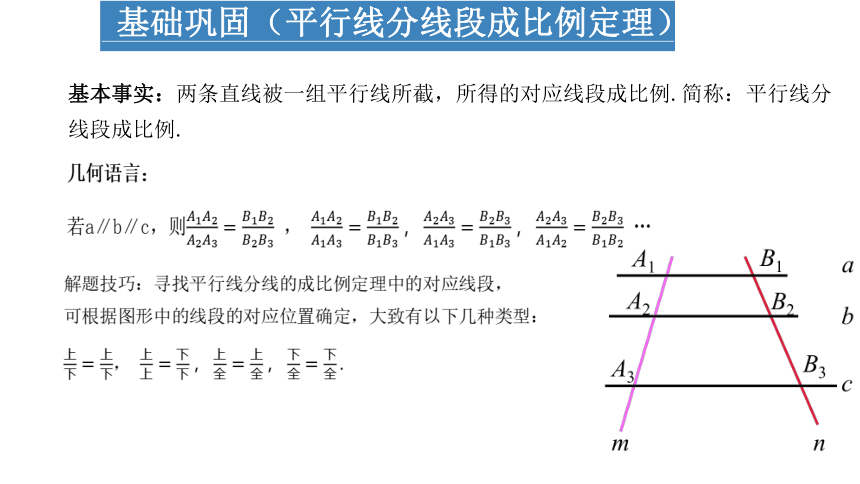
基础巩固(平行线分线段成比例定理)
几何语言:
若a∥b∥c,则 , …
基本事实:两条直线被一组平行线所截,所得的对应线段成比例.简称:平行线分线段成比例.
解题技巧:寻找平行线分线的成比例定理中的对应线段,
可根据图形中的线段的对应位置确定,大致有以下几种类型:,
基础巩固(平行线分线段成比例定理)
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A型
X型
A
D
B
E
C
A
D
B
E
C
基础巩固(相似三角形的判定)
相似三角形的判定方法:
1)定义法:对应角相等,对应边成比例的两个三角形相似.
2)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3)两边成比例且夹角相等的两个三角形相似.
4)三边成比例的两个三角形相似.
5)两角分别相等的两个三角形相似.
6)斜边和一条直角边成比例的两个直角三角形相似.
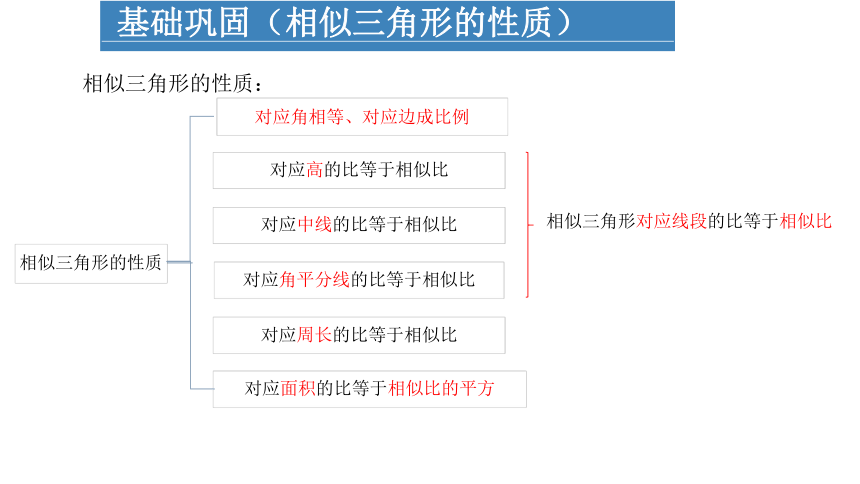
基础巩固(相似三角形的性质)
相似三角形的性质
对应高的比等于相似比
对应中线的比等于相似比
对应角平分线的比等于相似比
相似三角形对应线段的比等于相似比
对应周长的比等于相似比
对应面积的比等于相似比的平方
对应角相等、对应边成比例
相似三角形的性质:
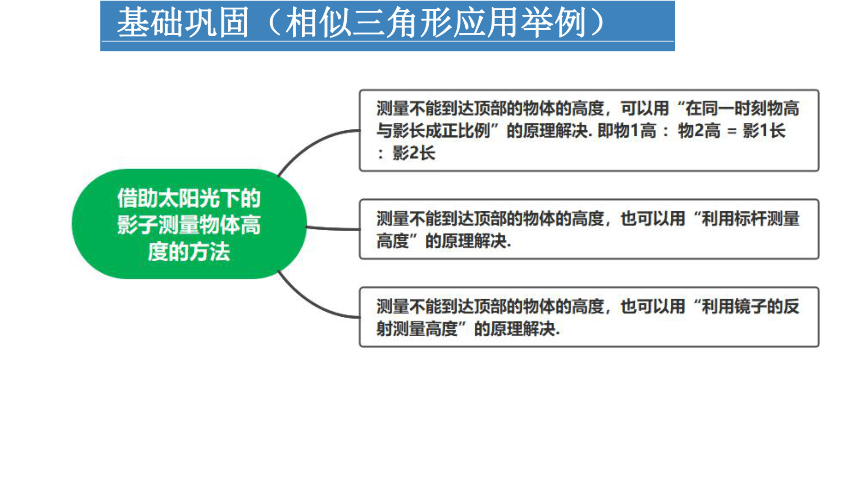
基础巩固(相似三角形应用举例)
基础巩固(相似三角形应用举例)
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的_____________________;
(3)利用相似三角形建立线段之间的关系,求出__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
基础巩固(相似三角形应用举例)
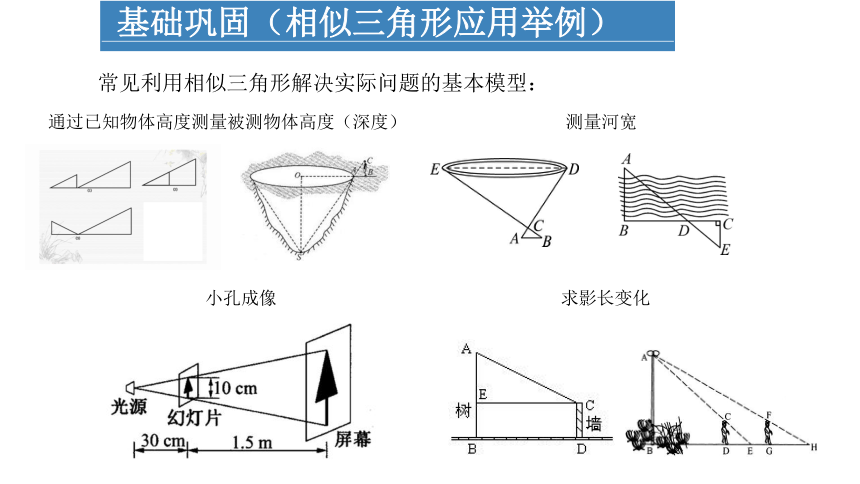
常见利用相似三角形解决实际问题的基本模型:
通过已知物体高度测量被测物体高度(深度)
测量河宽
小孔成像
求影长变化
基础巩固(位似)
如果两个图形的对应顶点的连线都经过同一点,且这点与对应顶点所连线段成比例,那么这两个图形叫做位似图形.点O是位似中心.
位似图形的性质:
1)位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3)对应线段平行或者在一条直线上.
基础巩固(位似)
对于两个多边形,如果它们的对应顶点的连线都经过同一点,且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形.
位似多边形的画法:
1) 确定位似中心.
2) 确定原图形的关键点(每对对应点都在位似中心的同侧或在位似中心的异侧).
3) 确定位似比.
4) 根据对应点所在直线经过位似中心且到位似中心的距离之比等于位似比,作出关键点的对应点,再按照原图的顺序连接各点.
基础巩固(位似)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比(新图与原图的相似比)为k,那么位似图形对应点的坐标的比等于k或-k,则图象上的对应点的坐标为(kx,ky)或(-kx,-ky).
热考题型
题型一(判定相似图形)
1、下列图形中不一定相似的是( )
A.两个矩形 B.两个圆
C.两个正方形 D.两个等边三角形
2、下图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到( )
A.轴对称 B.平移 C.旋转 D.相似
题型二(相似图形的性质)
1. 如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
2. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为18,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
3. 一个四边形的边长分别是4,5,6,7,另一个与它形状相同的四边形最短边长为8,则另一个四边形的周长是________.
44
题型三(比例线段)
1.已知3、4、5、x成比例,则x的值为( )
A. B. C. D.6
2.若线段a,b,c,d是成比例线段,且,,,则d=( )
A.8cm B.0.5cm C.2cm D.3cm
题型四(平行线分线段成比例定理)
1. 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
2.如图,,下面等式成立的是( )
A. B.
C. D.
【详解】∵DE∥FG∥BC,DB=4FB,∴=3.故选B.
题型四(平行线分线段成比例定理)
3.如图,已知直线a//b//c,直线m分别交直线a,b,c于点A,B,C;直线n分别交直线a,b,c于点D,E,F.若,则=( )
A. B. C. D.1
4.如图,已知ABCDEF,若AC=6,CE=2,BD=3,则BF的长为( )
A.6 B.5.5 C.4 D.4.5
题型四(平行线分线段成比例定理)
5.如图,在中,,,若,则( )
A. B. C. D.
【详解】解: ,,
, 解得:故选C
题型四(平行线分线段成比例定理)
6.如图,,AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是( )
A. B.
C. D.
7. 如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,则CE的长为 .
【详解】∵,∴,∴,
∴BE=10,∴CE=BE-BD=10-6=4
题型四(平行线分线段成比例定理)
8. 如图,直线AD,BC交于点O,.若,,.则的值为 .
9. 如图,D是的边上的点,,E是的中点,求:的值.
解:过点D作的平行线交BF于点P,如图
∴,
∵BD:DC=2:1 ,E是 AD 的中点,
∴,
∴∴
题型五(判定相似三角形)
1.已知的三边长分别是,,,的三边长如以下四个选项所列,若要使,则的三边长分别是( )
A.,, B.,, C.,, D.,,
【详解】解:A.∵,∴的三边长不可能是,,,故A错误;
B.∵,∴的三边长可能是,,,故B正确;
C.∵,∴的三边长不可能是,,,故C错误;
D.∵∴的三边长不可能是,,,故D错误.
故选:B.
题型五(判定相似三角形)
2.下列四个三角形中,与图中的三角形相似的是( )
【详解】
解:设单位正方形的边长为1,给出的三角形三边长分别为,2,.
A、三角形三边2,,3,与给出的三角形的各边不成比例,故A选项错误;
B、三角形三边2,4,2,与给出的三角形的各边成正比例,故B选项正确;
C、三角形三边2,3,,与给出的三角形的各边不成比例,故C选项错误;
D、三角形三边,4,,与给出的三角形的各边不成比例,故D选项错误.
故选:B.
题型五(判定相似三角形)
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C. D.
4 .如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与相似的是( )
题型五(判定相似三角形)
5.如图,在△ABC中,AB=6,AC=8,点D、E分别在线段AB、AC上,BD=2,CE=5,求证:△AED∽△ABC.
证明:∵AB=6,AC=8,BD=2,CE=5,
∴,,
∵,,∴=,
又∵∠DAE=∠CAB,
∴△AED∽△ABC.
题型五(判定相似三角形)
6.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C. D.
7. 如图,D是△ABC的边AB上一点,下列条件:①∠ACD=∠B;②;③=;④∠B=∠ACB,其中一定使△ABC∽△ACD的有( )
A.1个 B.2个 C.3个 D.4个
题型五(判定相似三角形)
8.如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC
【详解】证明:∵AD⊥AB,BE⊥AB,
∴∠DAC=90°=∠EBC,
∴∠D+∠ACD=90°,∠E+∠ECB=90°,
∵∠DCE=90°,
∴∠DCA+∠ECB=90°,
∴∠D=∠ECB,
∵∠DAC=90°=∠EBC,
∴△ACD∽△BEC.
题型五(判定相似三角形)
9. 如图所示,下列条件中能单独判断△ABC∽△ACD的个数是( )个.
①∠ABC=∠ACD;②∠ADC=∠ACB;③=;④AC2=AD AB
A.1 B.2 C.3 D.4
10 如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是( )
A. B. C. D.
题型六(相似三角形的性质)
1.如图,经过的重心,点是的中点,过点作交于点,
若,则线段GE的长为( )
A.6 B.4 C.5 D.3
【详解】解:∵经过的重心,∴点D是BC中点,
∵BC=16,∴CD=BD=8,
∵GE∥BC,∴△AGE∽△ADC,
∵点E是AC中点,∴,即,
解得:GE=4,故选B.
题型六(相似三角形的性质)
2. 相似三角形对应边的比为1∶4,那么相似比为_________,
对应角平分线的比为______,对应高的比为_________,对应中线的比为______,
对应周长的比为__________,对应面积的比为_________.
1∶16
1∶4
1∶4
1∶4
1∶4
1∶4
题型六(相似三角形的性质)
3 把一个三角形变成和它相似的三角形,
1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
3)如果边长缩小到原来的一半,那么面积缩小为原来的__________。
4 若与相似且对应中线之比为,则周长之比和面积比分别是_________、____________.
5.已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是______.
25
10
3∶5
9∶25
12
题型六(相似三角形的性质)
6.如图,在中,,BC=4,为边上的一点,且.若的面积为,则的面积为( )
A. B. C. D.
解:∵,,
∴,∴,即,
解得,的面积为,
∴的面积为:,
故选C.
题型六(相似三角形的性质)
7.如图,在Rt△ABC中,∠C=90°.正方形EFCD的三个顶点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是_______.
【详解】∵四边形CDEF是正方形,
∴DE//BC,∠CDE=∠EFC=90°,EF=DE=CD=CF,
∴∠AED=∠B,∠ADE=∠EFB=90°,
∴△ADE∽△BEF,∴,即,
∴DE EF=2×3=6,
∴正方形CDEF的面积是6.
题型七(相似三角形的应用)
1.《孙子算经》是中国古代重要的数学著作.其中有首歌谣:今有竿不知其长,量得影长一丈五尺.立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺.同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),问竹竿长为几丈几尺?
【详解】设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,
影长五寸=0.5尺,
∴,解得x=45(尺),
答:竹竿的长为四丈五尺.
题型七(相似三角形的应用)
2.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.
【详解】解:如图,过点N作ND⊥PQ于D,则DN=PM,
∴△ABC∽△QDN,.
∵AB=2米,BC=1.6米,PM=1.2米,NM=0.8米,
QD==1.5 米
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木杆PQ的长度为2.3米.
题型七(相似三角形的应用)
3. 如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,求该古城墙的高度.
【详解】
解:由镜面反射原理知∠APB=∠CPD.
∵AB⊥BD,CD⊥BD,∴∠ABP=∠CDP.
∵∠ABP=∠CDP,∠APB=∠CPD,
∴△ABP∽△CDP,∴AB∶BP=CD∶DP.
∵AB=1.2米,BP=1.8米,DP=12米,
∴CD= =8(米).
答:该古城墙的高度是8米
题型七(相似三角形的应用)
4. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
【详解】∵CB⊥AD,ED⊥AD,∴∠CBA=∠EDA=90°,
∵∠CAB=∠EAD,∴ ABC∽ ADE,∴,
又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,
∴,∴AB=17,即河宽为17米.
题型七(相似三角形的应用)
5 . 学习相似三角形相关知识后,善于思考的小明和小颖两位同学想通过所学计算桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点,再在河岸的这一边选出点和点,分别在、的延长线上取点、,使得.经测量,米,米,且点到河岸的距离为60米.已知于点,请你根据提供的数据,帮助他们计算桥AF的长度.
【详解】解:如图所示,过作于,
DE∥BC,,
,,
,.,
,即
解得,
答:桥AF的长度为90米.
题型七(相似三角形的应用)
6 如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( )
A.40 cm2 B.20 cm2
C.25 cm2 D.10 cm2
题型七(相似三角形的应用)
7 如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高为1.5米,那么路灯A的高度AB是( )
A.4.5米 B.6米 C.7.2米 D.8米
【详解】由题意知:MC∥AB,∴△DCM∽△DAB,∴=,即=,
∵NE∥AB,∴△FNE∽△FAB,∴=,即=,
∴=,解得:BC=3,∴=,解得:AB=6,
即路灯A的高度AB为6米,故选B.
题型八(位似)
1.如图,以点为位似中心,将△OAB放大后得到△OCD,,则____.
2.如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若,AC=3,则DC=_____.
题型八(位似)
3. 如图,与位似,点O是它们的位似中心,且位似比为1∶2,则与的周长之比是( )
A.1∶2 B.1∶4 C.1∶3 D.1∶9
4.如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
题型八(位似)
5. 如图,正方形网格图中的与是位似关系图,则位似中心是( )
A.点O B.点P C.点 D.点R
题型八(位似)
6.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,
在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
【详解】由题意得,△ODC∽△OBA,相似比是∴
又OB=6,AB=3,∴OD=2,CD=1,∴点C的坐标为:(2,1),故选A.
题型八(位似)
7. 如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点B的对应点B′的坐标是( )
A.(﹣3,﹣1) B.(﹣1,2)
C.(﹣9,1)或(9,﹣1) D.(﹣3,﹣1)或(3,1)
8.在平面直角坐标系中,已知点,,以原点O为位似中心,相似比为2,把放大,则点B的对应点的坐标( )
A. B.或 C. D.或
题型八(位似)
9. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
【详解】
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴=,∵BG=6,∴AD=BC=2,
∵AD∥BG,∴△OAD∽△OBG,∴ =,
∴=,解得:OA=1,∴OB=3,
∴C点坐标为:(3,2),故选A.
直击中考
真题
1.(2022·北京·统考中考真题)如图,在矩形中,若,则的长为 .
【详解】解:在矩形中, ,,
∴,,
∴,∴
真题
2.(2021·辽宁朝阳·统考中考真题)如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则S四边形EHFG
÷S菱形ABCD的值为( )
A. B. C. D.
【详解】解:∵BE=2AE,DF=2FC,∴,
∵G、H分别是AC的三等分点,∴,,∴,
∴EG∥BC∴,
同理可得HF∥AD,,∴,
故选:A.
真题
3.(2022·浙江丽水·中考真题)如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段的长是( )
A. B.1 C. D.2
【详解】解:过点作五条平行横线的垂线,交第三、四条直线,分别于、,
根据题意得,∵,∴,又∵AB=3,∴故选:C
4.(2022·陕西·中考真题)在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段BE的长为______米.
【详解】∵点E是AB的黄金分割点,∴.
∵AB=2米,∴米.
真题
5.(2022·江苏扬州·中考真题)如图,在中,,将以点为中心逆时针旋转得到,点在边上,交于点.下列结论:①;②平分;③,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
真题
6 (2022·上海·中考真题)如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上,,则_____.
【详解】解:∵D为AB中点,∴,即,
取AC中点E1,连接DE1,则DE1是△ABC的中位线,此时DE1∥BC,,
∴,在AC上取一点E2,使得DE1=DE2,则,
∵∠A=30°,∠B=90°,∴∠C=60°,BC=,
∵DE1∥BC,∴∠DE1E2=60°,∴△DE1E2是等边三角形,
∴DE1=DE2=E1E2=,∴E1E2=,
∵,∴,即,
综上,的值为:或,
真题
7.(2022·海南·中考真题)如图,点,将线段平移得到线段,若,则点D的坐标是( )
A. B. C. D.
真题
8.(2023重庆市中考)若两个相似三角形周长的比为,则这两个三角形对应边的比是( )
A. B. C. D.
9.(2023泰州市中考)两个相似图形的周长比为,则面积比为 .
10.(2023南通市中考)如图,在△ABC中点D、E分别为AB、AC的中点,则S△ADE:S△ABC= .
真题
11.(2023·四川南充·统考中考真题)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为( )
A. B. C. D.
真题
12.(2023·山东潍坊·统考中考真题)在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 米.
【详解】解:如图,过作于,交于H,
则,,,,
∴,
∵,∴∴,
∴,解得:,经检验符合题意;
∴(米);
真题
13.(2023·辽宁阜新真题)如图,与是以点为位似中心的位似图形,若,则与的面积比是 .
14.(2023·吉林长春真题)如图,和是以点为位似中心的位似图形,点在线段上.若,则和的周长之比为 .
真题
14.(2023·浙江·统考中考真题)如图,在直角坐标系中,的三个顶点分别为,现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形,则顶点的坐标是( )
A. B. C. D.
真题
15.(2023·四川遂宁·统考中考真题)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( )
A. B. C. D.
解:由图得:,
设直线的解析式为:,将点代入得:
,解得:,∴直线的解析式为:,
所在直线与BE所在直线x轴的交点坐标即为位似中心,
∴当时,,∴位似中心的坐标为,
故选:A.
相似
章节总结
第二十七章
学习目标
1.加深了解比例的基本性质、线段的比、成比例线段,认识图形的相似、位似等概念和性质;
2.理解相似图形的性质与判定、位似的性质与把一个图形放大或缩小,在同一坐标系下感受位似变换后点的坐标的变化规律.
中学阶段重点研究的两个平面图形间的关系是全等和相似,全等是一种特殊的相似.本章将在前面对全等形研究的基础上,借鉴全等三角形研究的基本套路对相似图形进行研究.本章研究的主要问题是相似图形的定义、性质和判定方法,研究的主要载体是三角形.此外,教科书在前面的章节中介绍了平移、轴对称和旋转三种图形的全等变换,本章将介绍一种新的图形变换-位似.
基础巩固(相似多边形相关概念)
相似多边形概念:
相似多边形的特征:
如果两个边数相同的多边形对应角相等、对应边成比例的两个多边形叫做相似多边形.
相似多边形的对应角相等、对应边成比例.
相似比概念:
相似多边形对应边的比叫做相似比.
相似多边形的表示:
相似多边形用符号“∽”表示,读作“相似于”.
【注意】在记两个相似多边形时,要把表示对应顶点的字母写在对应的位置上.
基础巩固(比例线段)
比例线段的概念:
对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如a:b=c:d(即ad=bc),我们就称四条线段是成比例线段,简称比例线段.
基础巩固(平行线分线段成比例定理)
几何语言:
若a∥b∥c,则 , …
基本事实:两条直线被一组平行线所截,所得的对应线段成比例.简称:平行线分线段成比例.
解题技巧:寻找平行线分线的成比例定理中的对应线段,
可根据图形中的线段的对应位置确定,大致有以下几种类型:,
基础巩固(平行线分线段成比例定理)
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A型
X型
A
D
B
E
C
A
D
B
E
C
基础巩固(相似三角形的判定)
相似三角形的判定方法:
1)定义法:对应角相等,对应边成比例的两个三角形相似.
2)平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3)两边成比例且夹角相等的两个三角形相似.
4)三边成比例的两个三角形相似.
5)两角分别相等的两个三角形相似.
6)斜边和一条直角边成比例的两个直角三角形相似.
基础巩固(相似三角形的性质)
相似三角形的性质
对应高的比等于相似比
对应中线的比等于相似比
对应角平分线的比等于相似比
相似三角形对应线段的比等于相似比
对应周长的比等于相似比
对应面积的比等于相似比的平方
对应角相等、对应边成比例
相似三角形的性质:
基础巩固(相似三角形应用举例)
基础巩固(相似三角形应用举例)
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的_____________________;
(3)利用相似三角形建立线段之间的关系,求出__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
基础巩固(相似三角形应用举例)
常见利用相似三角形解决实际问题的基本模型:
通过已知物体高度测量被测物体高度(深度)
测量河宽
小孔成像
求影长变化
基础巩固(位似)
如果两个图形的对应顶点的连线都经过同一点,且这点与对应顶点所连线段成比例,那么这两个图形叫做位似图形.点O是位似中心.
位似图形的性质:
1)位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3)对应线段平行或者在一条直线上.
基础巩固(位似)
对于两个多边形,如果它们的对应顶点的连线都经过同一点,且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形.
位似多边形的画法:
1) 确定位似中心.
2) 确定原图形的关键点(每对对应点都在位似中心的同侧或在位似中心的异侧).
3) 确定位似比.
4) 根据对应点所在直线经过位似中心且到位似中心的距离之比等于位似比,作出关键点的对应点,再按照原图的顺序连接各点.
基础巩固(位似)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比(新图与原图的相似比)为k,那么位似图形对应点的坐标的比等于k或-k,则图象上的对应点的坐标为(kx,ky)或(-kx,-ky).
热考题型
题型一(判定相似图形)
1、下列图形中不一定相似的是( )
A.两个矩形 B.两个圆
C.两个正方形 D.两个等边三角形
2、下图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到( )
A.轴对称 B.平移 C.旋转 D.相似
题型二(相似图形的性质)
1. 如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
2. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为18,则这个多边形的最短边长为( )
A.6 B.8 C.12 D.10
3. 一个四边形的边长分别是4,5,6,7,另一个与它形状相同的四边形最短边长为8,则另一个四边形的周长是________.
44
题型三(比例线段)
1.已知3、4、5、x成比例,则x的值为( )
A. B. C. D.6
2.若线段a,b,c,d是成比例线段,且,,,则d=( )
A.8cm B.0.5cm C.2cm D.3cm
题型四(平行线分线段成比例定理)
1. 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
2.如图,,下面等式成立的是( )
A. B.
C. D.
【详解】∵DE∥FG∥BC,DB=4FB,∴=3.故选B.
题型四(平行线分线段成比例定理)
3.如图,已知直线a//b//c,直线m分别交直线a,b,c于点A,B,C;直线n分别交直线a,b,c于点D,E,F.若,则=( )
A. B. C. D.1
4.如图,已知ABCDEF,若AC=6,CE=2,BD=3,则BF的长为( )
A.6 B.5.5 C.4 D.4.5
题型四(平行线分线段成比例定理)
5.如图,在中,,,若,则( )
A. B. C. D.
【详解】解: ,,
, 解得:故选C
题型四(平行线分线段成比例定理)
6.如图,,AF交BE于点G,若AC=CG,AG=FG,则下列结论错误的是( )
A. B.
C. D.
7. 如图,已知AB∥CD∥EF,AD:AF=3:5,BC=6,则CE的长为 .
【详解】∵,∴,∴,
∴BE=10,∴CE=BE-BD=10-6=4
题型四(平行线分线段成比例定理)
8. 如图,直线AD,BC交于点O,.若,,.则的值为 .
9. 如图,D是的边上的点,,E是的中点,求:的值.
解:过点D作的平行线交BF于点P,如图
∴,
∵BD:DC=2:1 ,E是 AD 的中点,
∴,
∴∴
题型五(判定相似三角形)
1.已知的三边长分别是,,,的三边长如以下四个选项所列,若要使,则的三边长分别是( )
A.,, B.,, C.,, D.,,
【详解】解:A.∵,∴的三边长不可能是,,,故A错误;
B.∵,∴的三边长可能是,,,故B正确;
C.∵,∴的三边长不可能是,,,故C错误;
D.∵∴的三边长不可能是,,,故D错误.
故选:B.
题型五(判定相似三角形)
2.下列四个三角形中,与图中的三角形相似的是( )
【详解】
解:设单位正方形的边长为1,给出的三角形三边长分别为,2,.
A、三角形三边2,,3,与给出的三角形的各边不成比例,故A选项错误;
B、三角形三边2,4,2,与给出的三角形的各边成正比例,故B选项正确;
C、三角形三边2,3,,与给出的三角形的各边不成比例,故C选项错误;
D、三角形三边,4,,与给出的三角形的各边不成比例,故D选项错误.
故选:B.
题型五(判定相似三角形)
3.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C. D.
4 .如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与相似的是( )
题型五(判定相似三角形)
5.如图,在△ABC中,AB=6,AC=8,点D、E分别在线段AB、AC上,BD=2,CE=5,求证:△AED∽△ABC.
证明:∵AB=6,AC=8,BD=2,CE=5,
∴,,
∵,,∴=,
又∵∠DAE=∠CAB,
∴△AED∽△ABC.
题型五(判定相似三角形)
6.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC C. D.
7. 如图,D是△ABC的边AB上一点,下列条件:①∠ACD=∠B;②;③=;④∠B=∠ACB,其中一定使△ABC∽△ACD的有( )
A.1个 B.2个 C.3个 D.4个
题型五(判定相似三角形)
8.如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC
【详解】证明:∵AD⊥AB,BE⊥AB,
∴∠DAC=90°=∠EBC,
∴∠D+∠ACD=90°,∠E+∠ECB=90°,
∵∠DCE=90°,
∴∠DCA+∠ECB=90°,
∴∠D=∠ECB,
∵∠DAC=90°=∠EBC,
∴△ACD∽△BEC.
题型五(判定相似三角形)
9. 如图所示,下列条件中能单独判断△ABC∽△ACD的个数是( )个.
①∠ABC=∠ACD;②∠ADC=∠ACB;③=;④AC2=AD AB
A.1 B.2 C.3 D.4
10 如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是( )
A. B. C. D.
题型六(相似三角形的性质)
1.如图,经过的重心,点是的中点,过点作交于点,
若,则线段GE的长为( )
A.6 B.4 C.5 D.3
【详解】解:∵经过的重心,∴点D是BC中点,
∵BC=16,∴CD=BD=8,
∵GE∥BC,∴△AGE∽△ADC,
∵点E是AC中点,∴,即,
解得:GE=4,故选B.
题型六(相似三角形的性质)
2. 相似三角形对应边的比为1∶4,那么相似比为_________,
对应角平分线的比为______,对应高的比为_________,对应中线的比为______,
对应周长的比为__________,对应面积的比为_________.
1∶16
1∶4
1∶4
1∶4
1∶4
1∶4
题型六(相似三角形的性质)
3 把一个三角形变成和它相似的三角形,
1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
3)如果边长缩小到原来的一半,那么面积缩小为原来的__________。
4 若与相似且对应中线之比为,则周长之比和面积比分别是_________、____________.
5.已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是______.
25
10
3∶5
9∶25
12
题型六(相似三角形的性质)
6.如图,在中,,BC=4,为边上的一点,且.若的面积为,则的面积为( )
A. B. C. D.
解:∵,,
∴,∴,即,
解得,的面积为,
∴的面积为:,
故选C.
题型六(相似三角形的性质)
7.如图,在Rt△ABC中,∠C=90°.正方形EFCD的三个顶点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是_______.
【详解】∵四边形CDEF是正方形,
∴DE//BC,∠CDE=∠EFC=90°,EF=DE=CD=CF,
∴∠AED=∠B,∠ADE=∠EFB=90°,
∴△ADE∽△BEF,∴,即,
∴DE EF=2×3=6,
∴正方形CDEF的面积是6.
题型七(相似三角形的应用)
1.《孙子算经》是中国古代重要的数学著作.其中有首歌谣:今有竿不知其长,量得影长一丈五尺.立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺.同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),问竹竿长为几丈几尺?
【详解】设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,
影长五寸=0.5尺,
∴,解得x=45(尺),
答:竹竿的长为四丈五尺.
题型七(相似三角形的应用)
2.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.
【详解】解:如图,过点N作ND⊥PQ于D,则DN=PM,
∴△ABC∽△QDN,.
∵AB=2米,BC=1.6米,PM=1.2米,NM=0.8米,
QD==1.5 米
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木杆PQ的长度为2.3米.
题型七(相似三角形的应用)
3. 如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,求该古城墙的高度.
【详解】
解:由镜面反射原理知∠APB=∠CPD.
∵AB⊥BD,CD⊥BD,∴∠ABP=∠CDP.
∵∠ABP=∠CDP,∠APB=∠CPD,
∴△ABP∽△CDP,∴AB∶BP=CD∶DP.
∵AB=1.2米,BP=1.8米,DP=12米,
∴CD= =8(米).
答:该古城墙的高度是8米
题型七(相似三角形的应用)
4. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
【详解】∵CB⊥AD,ED⊥AD,∴∠CBA=∠EDA=90°,
∵∠CAB=∠EAD,∴ ABC∽ ADE,∴,
又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,
∴,∴AB=17,即河宽为17米.
题型七(相似三角形的应用)
5 . 学习相似三角形相关知识后,善于思考的小明和小颖两位同学想通过所学计算桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点,再在河岸的这一边选出点和点,分别在、的延长线上取点、,使得.经测量,米,米,且点到河岸的距离为60米.已知于点,请你根据提供的数据,帮助他们计算桥AF的长度.
【详解】解:如图所示,过作于,
DE∥BC,,
,,
,.,
,即
解得,
答:桥AF的长度为90米.
题型七(相似三角形的应用)
6 如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( )
A.40 cm2 B.20 cm2
C.25 cm2 D.10 cm2
题型七(相似三角形的应用)
7 如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高为1.5米,那么路灯A的高度AB是( )
A.4.5米 B.6米 C.7.2米 D.8米
【详解】由题意知:MC∥AB,∴△DCM∽△DAB,∴=,即=,
∵NE∥AB,∴△FNE∽△FAB,∴=,即=,
∴=,解得:BC=3,∴=,解得:AB=6,
即路灯A的高度AB为6米,故选B.
题型八(位似)
1.如图,以点为位似中心,将△OAB放大后得到△OCD,,则____.
2.如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若,AC=3,则DC=_____.
题型八(位似)
3. 如图,与位似,点O是它们的位似中心,且位似比为1∶2,则与的周长之比是( )
A.1∶2 B.1∶4 C.1∶3 D.1∶9
4.如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶5
题型八(位似)
5. 如图,正方形网格图中的与是位似关系图,则位似中心是( )
A.点O B.点P C.点 D.点R
题型八(位似)
6.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,
在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
【详解】由题意得,△ODC∽△OBA,相似比是∴
又OB=6,AB=3,∴OD=2,CD=1,∴点C的坐标为:(2,1),故选A.
题型八(位似)
7. 如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点B的对应点B′的坐标是( )
A.(﹣3,﹣1) B.(﹣1,2)
C.(﹣9,1)或(9,﹣1) D.(﹣3,﹣1)或(3,1)
8.在平面直角坐标系中,已知点,,以原点O为位似中心,相似比为2,把放大,则点B的对应点的坐标( )
A. B.或 C. D.或
题型八(位似)
9. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
【详解】
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,
∴=,∵BG=6,∴AD=BC=2,
∵AD∥BG,∴△OAD∽△OBG,∴ =,
∴=,解得:OA=1,∴OB=3,
∴C点坐标为:(3,2),故选A.
直击中考
真题
1.(2022·北京·统考中考真题)如图,在矩形中,若,则的长为 .
【详解】解:在矩形中, ,,
∴,,
∴,∴
真题
2.(2021·辽宁朝阳·统考中考真题)如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则S四边形EHFG
÷S菱形ABCD的值为( )
A. B. C. D.
【详解】解:∵BE=2AE,DF=2FC,∴,
∵G、H分别是AC的三等分点,∴,,∴,
∴EG∥BC∴,
同理可得HF∥AD,,∴,
故选:A.
真题
3.(2022·浙江丽水·中考真题)如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段的长是( )
A. B.1 C. D.2
【详解】解:过点作五条平行横线的垂线,交第三、四条直线,分别于、,
根据题意得,∵,∴,又∵AB=3,∴故选:C
4.(2022·陕西·中考真题)在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段BE的长为______米.
【详解】∵点E是AB的黄金分割点,∴.
∵AB=2米,∴米.
真题
5.(2022·江苏扬州·中考真题)如图,在中,,将以点为中心逆时针旋转得到,点在边上,交于点.下列结论:①;②平分;③,其中所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
真题
6 (2022·上海·中考真题)如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上,,则_____.
【详解】解:∵D为AB中点,∴,即,
取AC中点E1,连接DE1,则DE1是△ABC的中位线,此时DE1∥BC,,
∴,在AC上取一点E2,使得DE1=DE2,则,
∵∠A=30°,∠B=90°,∴∠C=60°,BC=,
∵DE1∥BC,∴∠DE1E2=60°,∴△DE1E2是等边三角形,
∴DE1=DE2=E1E2=,∴E1E2=,
∵,∴,即,
综上,的值为:或,
真题
7.(2022·海南·中考真题)如图,点,将线段平移得到线段,若,则点D的坐标是( )
A. B. C. D.
真题
8.(2023重庆市中考)若两个相似三角形周长的比为,则这两个三角形对应边的比是( )
A. B. C. D.
9.(2023泰州市中考)两个相似图形的周长比为,则面积比为 .
10.(2023南通市中考)如图,在△ABC中点D、E分别为AB、AC的中点,则S△ADE:S△ABC= .
真题
11.(2023·四川南充·统考中考真题)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为( )
A. B. C. D.
真题
12.(2023·山东潍坊·统考中考真题)在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 米.
【详解】解:如图,过作于,交于H,
则,,,,
∴,
∵,∴∴,
∴,解得:,经检验符合题意;
∴(米);
真题
13.(2023·辽宁阜新真题)如图,与是以点为位似中心的位似图形,若,则与的面积比是 .
14.(2023·吉林长春真题)如图,和是以点为位似中心的位似图形,点在线段上.若,则和的周长之比为 .
真题
14.(2023·浙江·统考中考真题)如图,在直角坐标系中,的三个顶点分别为,现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形,则顶点的坐标是( )
A. B. C. D.
真题
15.(2023·四川遂宁·统考中考真题)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( )
A. B. C. D.
解:由图得:,
设直线的解析式为:,将点代入得:
,解得:,∴直线的解析式为:,
所在直线与BE所在直线x轴的交点坐标即为位似中心,
∴当时,,∴位似中心的坐标为,
故选:A.
