安徽省合肥市第四十二中学2023-2024年九年级上学期期中数学试题(含简单答案)
文档属性
| 名称 | 安徽省合肥市第四十二中学2023-2024年九年级上学期期中数学试题(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 880.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 00:00:00 | ||
图片预览


文档简介
合肥市42中学2023-2024学年度第一学期期中绿色评价
九年级数学学科试题卷
一、选择题(本大题共10小题,每小题4分,满分共40分)
1.函数的图像的顶点坐标是()
A. B. C. D.
2.下列二次函数的图象开口向上的是()
A. B. C. D.
3.下列线段a、b、c、d是成比例线段的是()
A.,,, B.,,,
C.,,, D.,,,
4.将抛物线向右平移1个单位,再向下平移6个单位后所得抛物线的解析式为()
A. B. C. D.
5.对于一次函数,如果y随x的增大而减小,那么反比例函数满足()
A.当时, B.在每个象限内,y随x的增大而减小
C.图像分布在第一、三象限 D.图像分布在第二、四象限
6.如图所示,点P是的边上一点,连接,以下条件中不能判定的是()
A. B. C. D.
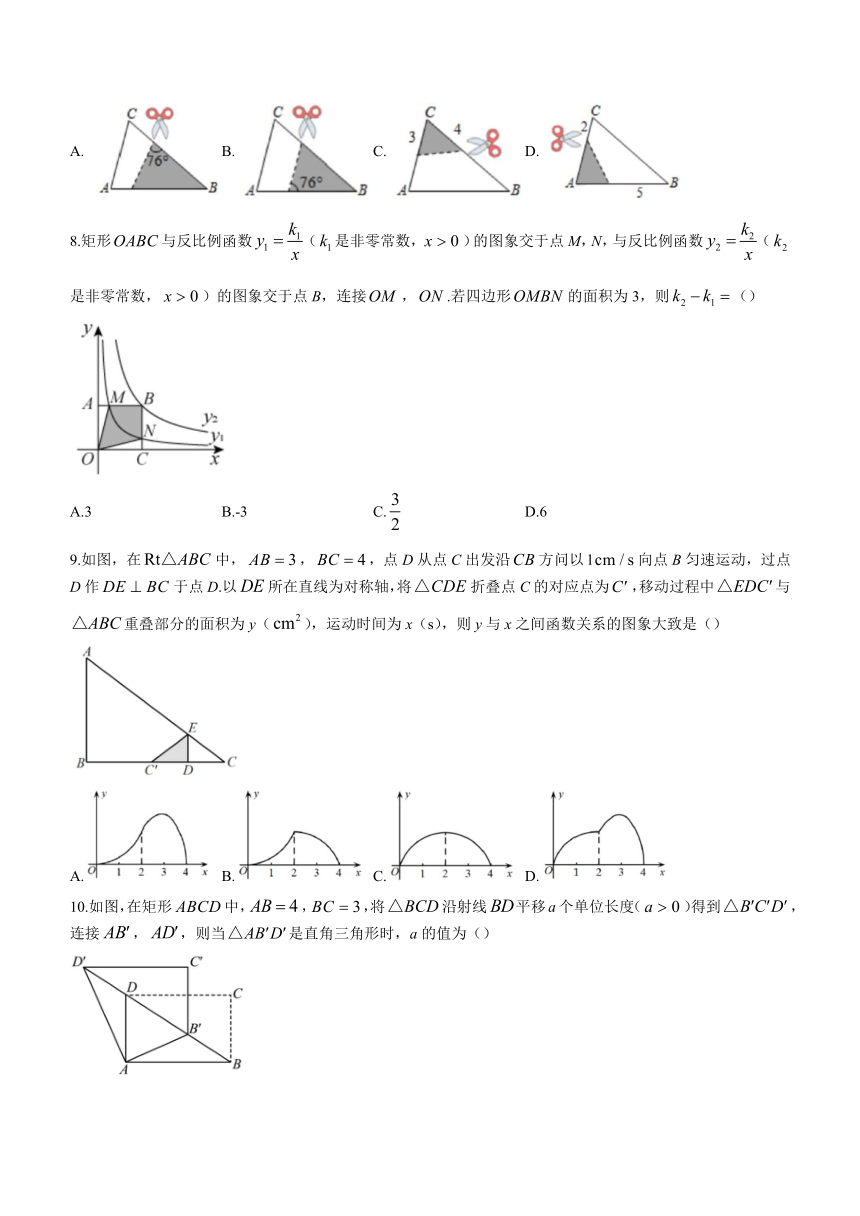
7.如图,中,,,.将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()
A. B. C. D.
8.矩形与反比例函数(是非零常数,)的图象交于点M,N,与反比例函数(是非零常数,)的图象交于点B,连接,.若四边形的面积为3,则()
A.3 B.-3 C. D.6
9.如图,在中,,,点D从点C出发沿方问以l向点B匀速运动,过点D作于点D.以所在直线为对称轴,将折叠点C的对应点为,移动过程中与重叠部分的面积为y(),运动时间为x(s),则y与x之间函数关系的图象大致是()
A. B. C. D.
10.如图,在矩形中,,,将沿射线平移a个单位长度()得到,连接,,则当是直角三角形时,a的值为()
A.或 B.2或 C.或 D.或3
二、填空题(本大题共4小题,每小题5分,满分共20分)
11.若二次函数与x轴有两个交点,则k的取值范围是________.
12.在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如下图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为_______米.
13.如上图,E是平行四边形边的延长线上一点,,则________.
14.如下图.已知反比例与(,)的图象如图所示,点A,B在的图象上,点C,D在的图象上,对角线于点P,对角线轴.已知点B的横坐标为4.
(1)当,,且P为中点,判断四边形的形状为__________.
(2)当四边形为正方形时m,n之间的数量关系为_____________.
三、解答题(本大题共2小题,每小题8分,满分共16分)
15.已知抛物线的顶点是,且经过点,试确定抛物线的函数表达式.
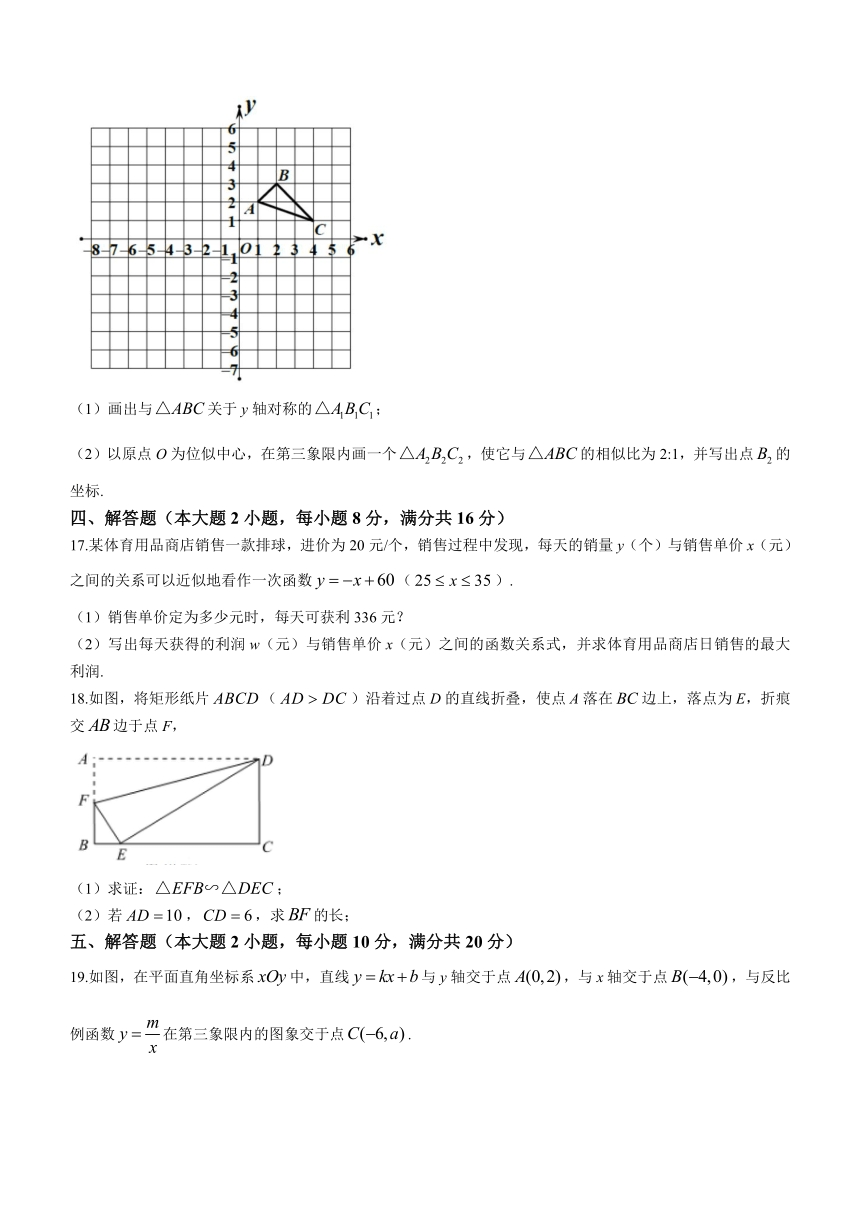
16.如图、在平面直角坐标系中,的三个顶点的坐标分别为,,
(1)画出与关于y轴对称的;
(2)以原点O为位似中心,在第三象限内画一个,使它与的相似比为2:1,并写出点的坐标.
四、解答题(本大题2小题,每小题8分,满分共16分)
17.某体育用品商店销售一款排球,进价为20元/个,销售过程中发现,每天的销量y(个)与销售单价x(元)之间的关系可以近似地看作一次函数().
(1)销售单价定为多少元时,每天可获利336元?
(2)写出每天获得的利润w(元)与销售单价x(元)之间的函数关系式,并求体育用品商店日销售的最大利润.
18.如图,将矩形纸片()沿着过点D的直线折叠,使点A落在边上,落点为E,折痕交边于点F,
(1)求证:;
(2)若,,求的长;
五、解答题(本大题2小题,每小题10分,满分共20分)
19.如图,在平面直角坐标系中,直线与y轴交于点,与x轴交于点,与反比例函数在第三象限内的图象交于点.
(1)求反比例函数的表达式;
(2)当时,求x的取值范围;
(3)当点P在y轴上,的面积为6时,直接写出点P的坐标.
20.如图,平分,交于点F,点C在的延长线上,,的延长线交于点E.
(1)求证:;
(2)若,,求的值
六、解答题(本大题2小题,每小题12分,满分共24分)
21.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6,锅深3,锅盖高1(锅口直径与锅盖直径视为相同),建立直角坐标系如图所示,如果把锅纵断面的抛物线记为,把锅盖纵断面的抛物线记为.
(1)求和的解析式;
(2)如果炒菜时锅的水位高度是1,求此时水面的直径;
(3)如果将一个底面直径为3,高度为3.2的圆柱形器皿放入炒菜
锅内蒸食物,锅盖能否正常盖上?请说明理由.
22.在中,,点D是边上一点,,,和交于点E.
图1图2
(1)如图1,如果,求证:;
(2)如图2,如果,猜想和之间的数量关系,并证明你的结论;
(3)在(2)的情况下,如果,,,请直接写出的长.
七、解答题(本题满分14分)
23.如图,抛物线()经过点、,交y轴于点.D为抛物线在第三象限部分上的一点,作轴于点E,交线段于点F,连接.
(1)求抛物线的表达式;
(2)求线段长度的最大值,并求此时D点的坐标;
(3)若线段把分成面积比为1∶2的两部分,求此时点E的坐标.
合肥市42中学2023-2024学年度第一学期期中九年级数学参考答案:
1.C2.A3.C4.D5.D6.B7.C8.A9.A10.A
11.且
12.
13.1∶2
14.(1)菱形;(2)
15.抛物线的表达式为.
16.点的坐标为.
17.(1)销售单价定为32元时,每天可获利336元;
(2)日销售最大利润为375元
18.(1)略;(2)
19.(1)反比例函数的解析式是;
(2)自变量x的取值范围为或.;
(3)点P的坐标为或
20.(1)略;(2)1∶16
21.(1):();:()
(2)水面的直径为
(3),锅盖不能正常盖上,
22.(1)略;(2);(3)
23.(1);
(2)线段长度的最大值是,此时D的坐标为
(3)满足条件
九年级数学学科试题卷
一、选择题(本大题共10小题,每小题4分,满分共40分)
1.函数的图像的顶点坐标是()
A. B. C. D.
2.下列二次函数的图象开口向上的是()
A. B. C. D.
3.下列线段a、b、c、d是成比例线段的是()
A.,,, B.,,,
C.,,, D.,,,
4.将抛物线向右平移1个单位,再向下平移6个单位后所得抛物线的解析式为()
A. B. C. D.
5.对于一次函数,如果y随x的增大而减小,那么反比例函数满足()
A.当时, B.在每个象限内,y随x的增大而减小
C.图像分布在第一、三象限 D.图像分布在第二、四象限
6.如图所示,点P是的边上一点,连接,以下条件中不能判定的是()
A. B. C. D.
7.如图,中,,,.将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()
A. B. C. D.
8.矩形与反比例函数(是非零常数,)的图象交于点M,N,与反比例函数(是非零常数,)的图象交于点B,连接,.若四边形的面积为3,则()
A.3 B.-3 C. D.6
9.如图,在中,,,点D从点C出发沿方问以l向点B匀速运动,过点D作于点D.以所在直线为对称轴,将折叠点C的对应点为,移动过程中与重叠部分的面积为y(),运动时间为x(s),则y与x之间函数关系的图象大致是()
A. B. C. D.
10.如图,在矩形中,,,将沿射线平移a个单位长度()得到,连接,,则当是直角三角形时,a的值为()
A.或 B.2或 C.或 D.或3
二、填空题(本大题共4小题,每小题5分,满分共20分)
11.若二次函数与x轴有两个交点,则k的取值范围是________.
12.在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如下图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为_______米.
13.如上图,E是平行四边形边的延长线上一点,,则________.
14.如下图.已知反比例与(,)的图象如图所示,点A,B在的图象上,点C,D在的图象上,对角线于点P,对角线轴.已知点B的横坐标为4.
(1)当,,且P为中点,判断四边形的形状为__________.
(2)当四边形为正方形时m,n之间的数量关系为_____________.
三、解答题(本大题共2小题,每小题8分,满分共16分)
15.已知抛物线的顶点是,且经过点,试确定抛物线的函数表达式.
16.如图、在平面直角坐标系中,的三个顶点的坐标分别为,,
(1)画出与关于y轴对称的;
(2)以原点O为位似中心,在第三象限内画一个,使它与的相似比为2:1,并写出点的坐标.
四、解答题(本大题2小题,每小题8分,满分共16分)
17.某体育用品商店销售一款排球,进价为20元/个,销售过程中发现,每天的销量y(个)与销售单价x(元)之间的关系可以近似地看作一次函数().
(1)销售单价定为多少元时,每天可获利336元?
(2)写出每天获得的利润w(元)与销售单价x(元)之间的函数关系式,并求体育用品商店日销售的最大利润.
18.如图,将矩形纸片()沿着过点D的直线折叠,使点A落在边上,落点为E,折痕交边于点F,
(1)求证:;
(2)若,,求的长;
五、解答题(本大题2小题,每小题10分,满分共20分)
19.如图,在平面直角坐标系中,直线与y轴交于点,与x轴交于点,与反比例函数在第三象限内的图象交于点.
(1)求反比例函数的表达式;
(2)当时,求x的取值范围;
(3)当点P在y轴上,的面积为6时,直接写出点P的坐标.
20.如图,平分,交于点F,点C在的延长线上,,的延长线交于点E.
(1)求证:;
(2)若,,求的值
六、解答题(本大题2小题,每小题12分,满分共24分)
21.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6,锅深3,锅盖高1(锅口直径与锅盖直径视为相同),建立直角坐标系如图所示,如果把锅纵断面的抛物线记为,把锅盖纵断面的抛物线记为.
(1)求和的解析式;
(2)如果炒菜时锅的水位高度是1,求此时水面的直径;
(3)如果将一个底面直径为3,高度为3.2的圆柱形器皿放入炒菜
锅内蒸食物,锅盖能否正常盖上?请说明理由.
22.在中,,点D是边上一点,,,和交于点E.
图1图2
(1)如图1,如果,求证:;
(2)如图2,如果,猜想和之间的数量关系,并证明你的结论;
(3)在(2)的情况下,如果,,,请直接写出的长.
七、解答题(本题满分14分)
23.如图,抛物线()经过点、,交y轴于点.D为抛物线在第三象限部分上的一点,作轴于点E,交线段于点F,连接.
(1)求抛物线的表达式;
(2)求线段长度的最大值,并求此时D点的坐标;
(3)若线段把分成面积比为1∶2的两部分,求此时点E的坐标.
合肥市42中学2023-2024学年度第一学期期中九年级数学参考答案:
1.C2.A3.C4.D5.D6.B7.C8.A9.A10.A
11.且
12.
13.1∶2
14.(1)菱形;(2)
15.抛物线的表达式为.
16.点的坐标为.
17.(1)销售单价定为32元时,每天可获利336元;
(2)日销售最大利润为375元
18.(1)略;(2)
19.(1)反比例函数的解析式是;
(2)自变量x的取值范围为或.;
(3)点P的坐标为或
20.(1)略;(2)1∶16
21.(1):();:()
(2)水面的直径为
(3),锅盖不能正常盖上,
22.(1)略;(2);(3)
23.(1);
(2)线段长度的最大值是,此时D的坐标为
(3)满足条件
同课章节目录
