旋转的简单应用(广东省中山市)
文档属性
| 名称 | 旋转的简单应用(广东省中山市) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-01 21:10:00 | ||
图片预览



文档简介
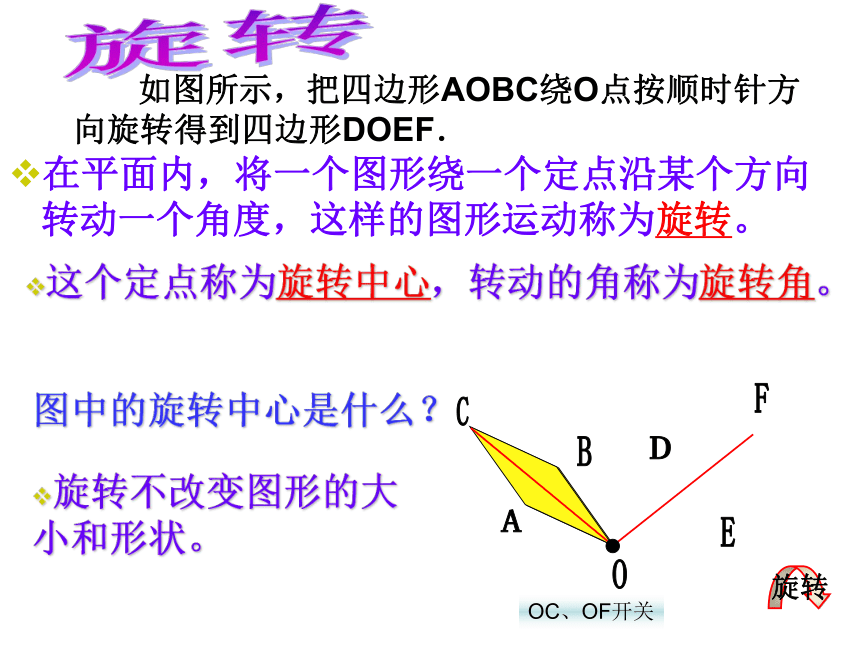
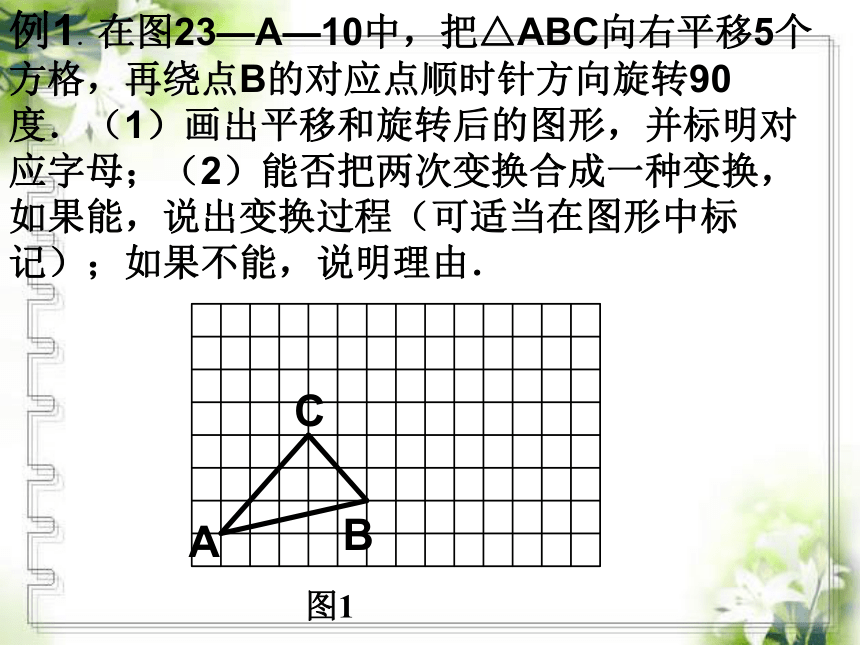
课件15张PPT。旋转的应用BACDEFO旋转OC、OF开关 如图所示,把四边形AOBC绕O点按顺时针方向旋转得到四边形DOEF.旋转在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为旋转中心,转动的角称为旋转角。图中的旋转中心是什么?旋转不改变图形的大小和形状。旋转的特征和性质经过旋转: 3.图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度.即旋转角相等.2.任意一对对应点与旋转中心所连的角都是旋转角.1.对应点到旋转中心的距离相等.BACDEFO1.经过旋转,点A和B移动到什么位置?2.AO与DO的长有什么关系?BO与EO呢?CO与OF呢?3.旋转角是什么?旋转的特征和性质4.它们有什么大小关系?例1.在图23—A—10中,把△ABC向右平移5个方格,再绕点B的对应点顺时针方向旋转90度.(1)画出平移和旋转后的图形,并标明对应字母;(2)能否把两次变换合成一种变换,如果能,说出变换过程(可适当在图形中标记);如果不能,说明理由.图1例2.如图,已知△ABC的顶点的坐标分别是
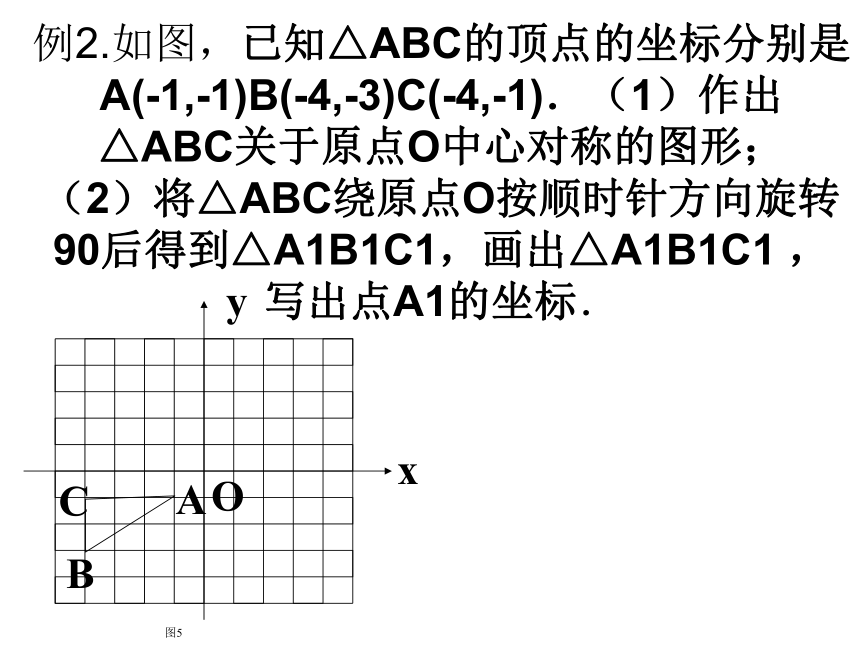
A(-1,-1)B(-4,-3)C(-4,-1).(1)作出△ABC关于原点O中心对称的图形;
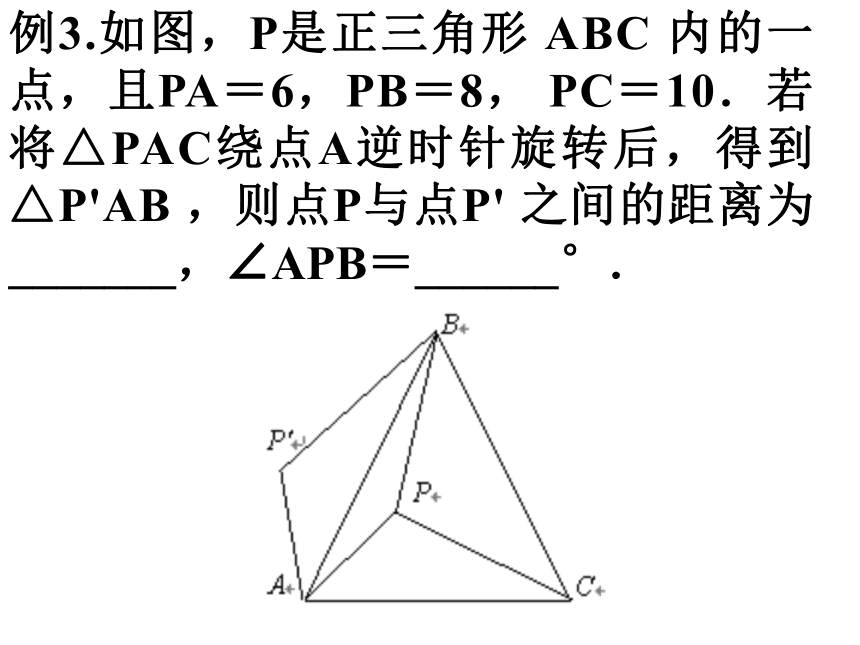
(2)将△ABC绕原点O按顺时针方向旋转90后得到△A1B1C1,画出△A1B1C1 ,写出点A1的坐标.运用旋转解决几何问题:平面几何中的旋转是一种重要的变换手段,运用它可以把题目中分散的元素加以集中,实现“化零为整”,有助于事半功倍的解决的问题。在条件中出现正方形、等边三角形、菱形,等腰三角形时,常可考虑用旋转变换构造全等三角形,以集中条件。例3.如图,P是正三角形 ABC 内的一点,且PA=6,PB=8, PC=10.若将△PAC绕点A逆时针旋转后,得到△P'AB ,则点P与点P' 之间的距离为_______,∠APB=______°.例4.如图,正方形ABCD中,AB= ,点E、F分别在BC、CD上,且 , ,求△AEF的面积。思考、(06龙岩)如图1,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠。(1)操作1:固定△ABC,将三角板沿CB方向平移,使其直角顶点落在BC的中点M.如图2。探究:三角板沿CB方向平移的距离是多少?(2)操作2:在(1)情况下,将三角板绕BC的中点M顺时针方向旋转角度а(0°<а<90°)如图3。探究:设三角板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,试说明其面积的变化情况。图2CMAB图3PQACBMa练习1.如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD在直线l上按顺时针方向不滑动的每秒90O转动,转动3秒后停止,则顶点A经过的路线长为 .练习2.如图,斜边长为6cm, ∠A=30o的直角三角板ABC绕点C顺时针方向旋转90o至ΔAˊBˊCˊ的位置,再沿CB向左平移使点Bˊ落在原三角板ABC的斜边AB上,则三角板向左平移的距离为________cm.( 06吉林)如图,在Rt⊿ABC和Rt⊿DEF中,∠ABC=900,AB=4,BC=6,∠DEF=900,DE=EF=4.
(1)移动⊿DEF ,使边DE与AB重合(如图1),再将⊿DEF沿AB所在直线向左平移,使点F落在AC上(如图2),求BE的长;
(2)将图2中的⊿DEF绕点A顺时针旋转,使点F落在BC上,连结AF(如图3).请找出图中的全等三角形,并说明它们全等的理由.(不再添加辅助线,不再标注其它字母).
通过本堂课的探究
你学到了......
你体会了......5.点金帚(学后反思 感悟收获)智慧小结回味无穷 图形变换来源于现实世界中的物体的运动和变化。悠悠岁月中人们从没有间断过对这种几何现象的探索,也没有停止过美化生活的脚步,可以说是生活呼吁我们研究图形的变换!
(1)移动⊿DEF ,使边DE与AB重合(如图1),再将⊿DEF沿AB所在直线向左平移,使点F落在AC上(如图2),求BE的长;
(2)将图2中的⊿DEF绕点A顺时针旋转,使点F落在BC上,连结AF(如图3).请找出图中的全等三角形,并说明它们全等的理由.(不再添加辅助线,不再标注其它字母).
通过本堂课的探究
你学到了......
你体会了......5.点金帚(学后反思 感悟收获)智慧小结回味无穷 图形变换来源于现实世界中的物体的运动和变化。悠悠岁月中人们从没有间断过对这种几何现象的探索,也没有停止过美化生活的脚步,可以说是生活呼吁我们研究图形的变换!
同课章节目录
