关于原点对称的点的坐标

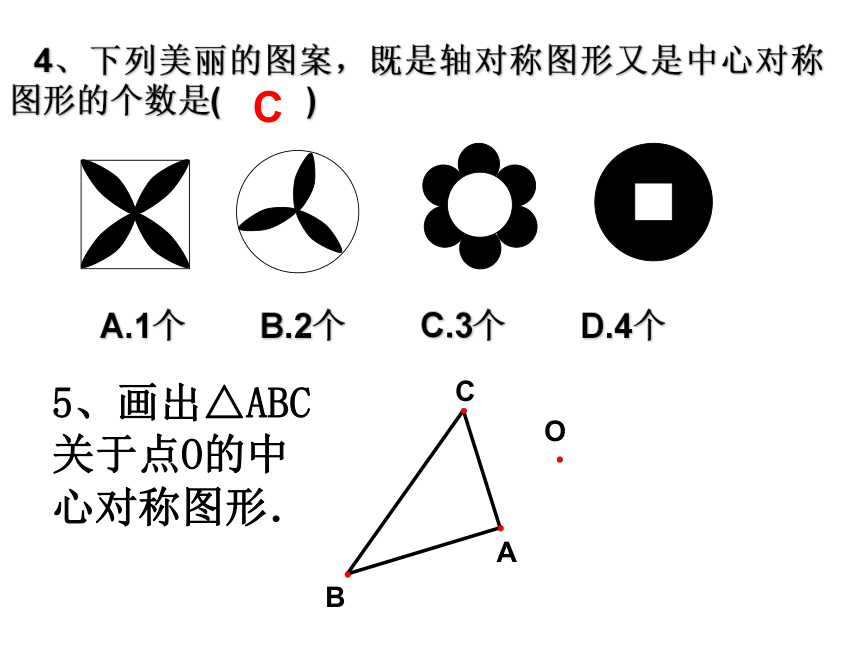
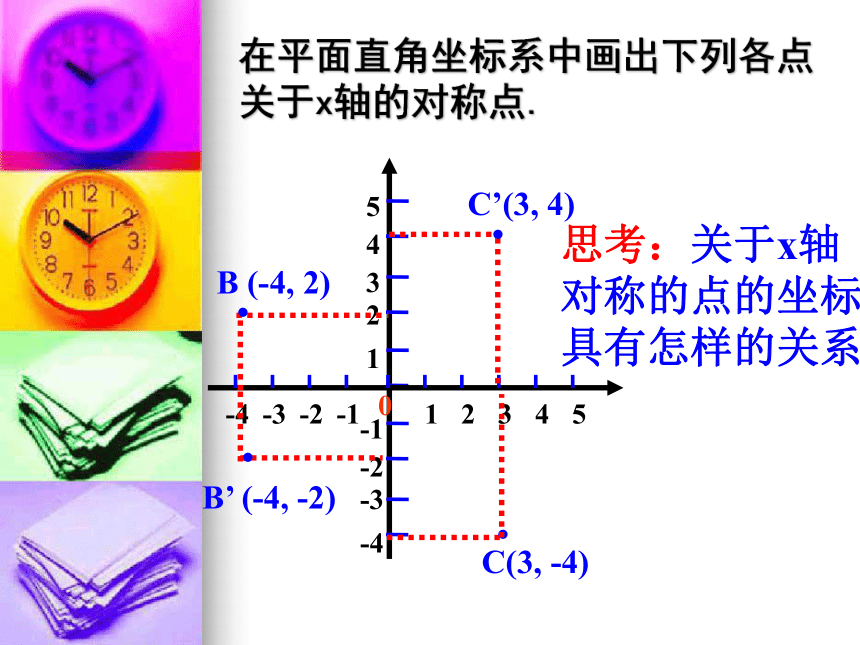
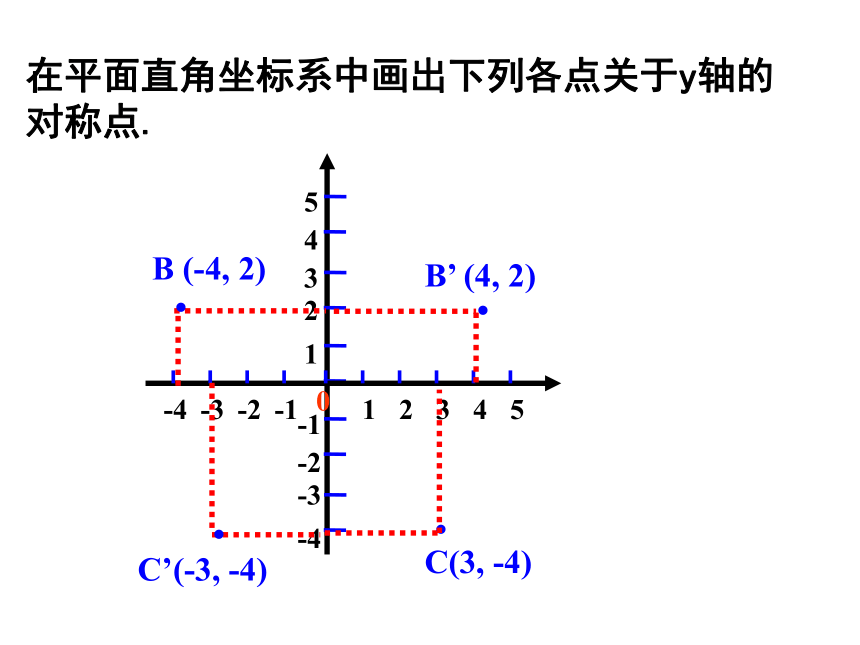
课件14张PPT。23.2.3关于原点对称的点的坐标☆知识巩固2、中心对称有何性质？1、什么叫中心对称和中心对称图形？（2）关于中心对称图形的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。（1）关于中心对称图形的两个图形是全等形。3、在下列图形中，是中心对称图形的是 （ ）C4、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是( )CA.1个 B.2个 C.3个 D.4个5、画出△ABC关于点O的中心对称图形． 在平面直角坐标系中画出下列各点关于x轴的对称点.B (-4, 2)··C(3, -4)·B’ (-4, -2)·C’(3, 4)思考：关于x轴对称的点的坐标具有怎样的关系？在平面直角坐标系中画出下列各点关于y轴的对称点.B (-4, 2)··C(3, -4)·B’ (4, 2)·C’(-3, -4)小结：在平面直角坐标系中，关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点（x, y）关于x轴对称的点的坐标为______.
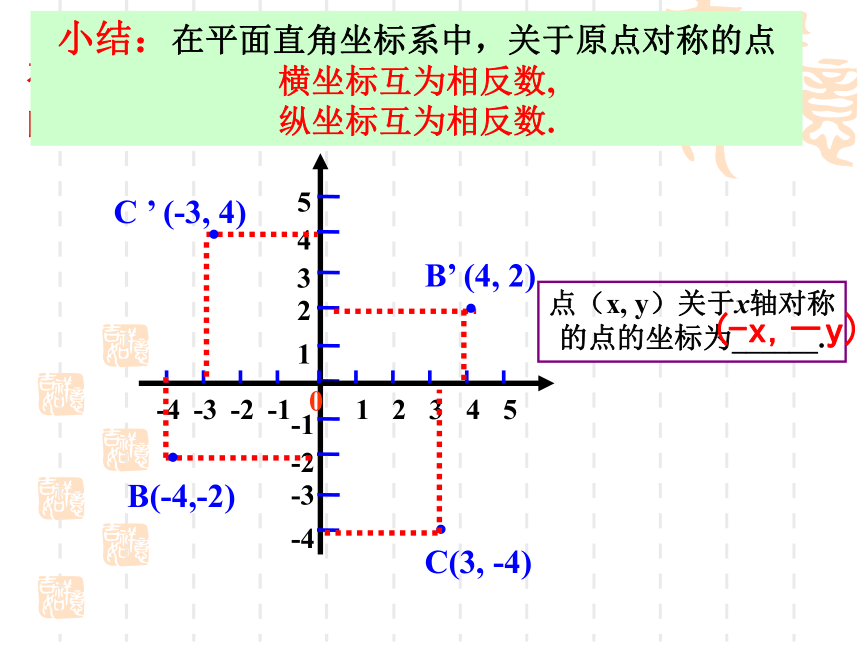
点（x, y）关于y轴对称的点的坐标为______.(x,－y)(－x,y)在平面直角坐标系中画出下列各点关于原点的对称点.C ’ (-3, 4)··C(3, -4)·B’ (4, 2)·B(-4,-2)小结：在平面直角坐标系中，关于原点对称的点
横坐标互为相反数,
纵坐标互为相反数.点（x, y）关于x轴对称
的点的坐标为______.(-x,－y)1、完成下表.
(-2, 3)(2,-3)(-1,-2)(1, -2)(6, 5)(-6, 5)(0, 1.6)(0,1.6)(-4,0)(4,0)2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称，则a=_____ b=_______.
若点p与点p’关于y轴对称，则a=_____ b=_______.
若点p与点p’关于原点对称，则a=_____ b=_______.练 习46-2023.下列图象中,一定关于原点对称的图象是( )
A.y=1/x B.y=2x+1 C.y=-2x+1 D.以上三种都有可能.例：已知△ABC的三个顶点的坐标分别为A(-3，5),B(- 4，1),C(-1，3)，作出△ABC关于原点对称的图形。解：点A(-3,5),B(-4,1),
C(-1,3)，关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.······-5ABC1．下列函数中，图象一定关于原点对称的图象是（ ）
A．y= B．y=2x+1
C．y=-2x+1 D．以上三种都不可能2．如果点P（-3，1），那么点P（-3，1）关于原点
的对称点P/的坐标是P/_______．3．写出函数y=- 与y= 具有的一个共同
性质________（用对称的观点写）．☆练一练4.教材P73 练习． ☆应用拓展如图，直线AB与x轴、y轴分别相交于A、B两点，将直线AB绕点O顺时针旋转90°得到直线A1B1．
（1）在图中画出直线A1B1．
（2）求出线段A1B1中点的反比例函数解析式．
（3）是否存在另一条与直线AB平行的直线y=kx+b，它与双曲线只有一个交点，若存在，求此直线的函数解析式，若不存在，请说明理由．1.四边形ABCD各顶点坐标分别为(5,0),　(-2,3)，（-1,0) ,(-1,5),作出与四边形ABCD关于原点O对称的图形.2.平行四边形,A(1,2), B(-4,2), C(-2,-5),求出第四个点D的坐标.若平行四边形在坐标系内关于原点对称,已知点A,点B的坐标不变,点C,点D的坐标又是什么?1、学习了在平面直角坐标系中，关于x轴和y轴对称的点的坐标的特点。关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.课 堂 小 结关于原点对称的点横坐标互为相反数,
纵坐标互为相反数.