等差数列与等比数列的性质(辽宁省本溪市)
文档属性
| 名称 | 等差数列与等比数列的性质(辽宁省本溪市) |  | |
| 格式 | rar | ||
| 文件大小 | 249.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-02 21:26:00 | ||
图片预览






文档简介
课件17张PPT。等差与等比数列的性质(1)等差数列的定义:(2)等比数列的定义:通项公式:通项公式:复习回顾阅读教材P76例题6、7引申1、如果{an} {bn}是等差数列,
证明:{pan+ qbn }(其中p,q是常数)也是等差数列(1)已知数列{ an }的通项公式是an =3n-1
求证:{an}为等差数列;(2) 已知数列{an}是等差数列,
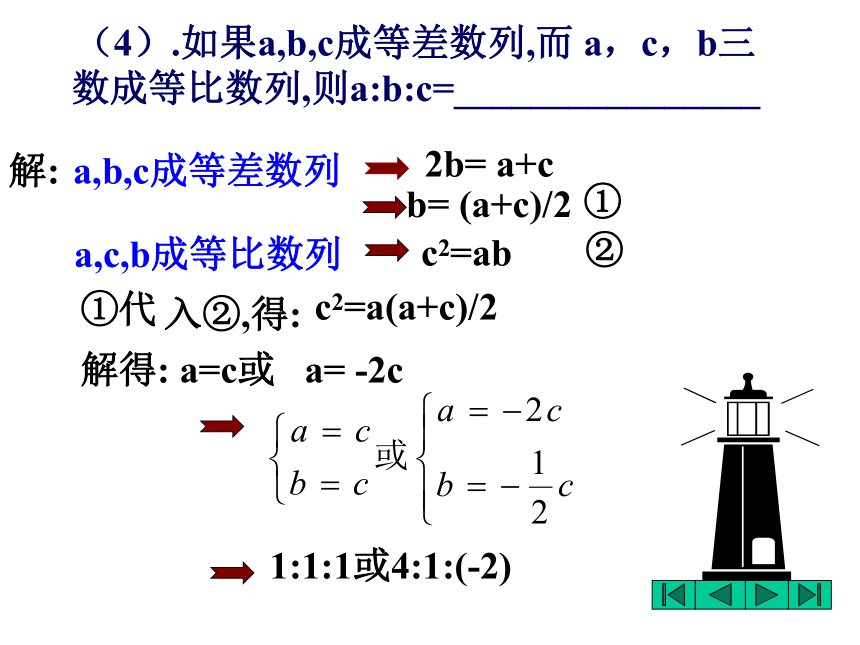
求证:数列{an+an+1}也是等差数列.例1根据等比数列的定义可知,数列{kanmbn}是一个以qq’为公比的等比数列.(4).如果a,b,c成等差数列,而 a,c,b三数成等比数列,则a:b:c=________________ a,b,c成等差数列2b= a+cb= (a+c)/2
a,c,b成等比数列c2=ab①②①代入②,得:c2=a(a+c)/2解得: a=c或 a= -2c1:1:1或4:1:(-2)解:例2.已知数列的通项公式为an=pn+q
其中p,q是常数,且p≠0,那么
这个数列是否是等差数列?如果
是,其首项与公差是什么? 等差数列的判定方法:
(1) an+1-an=d ? {an}是等差数列(2) 2an+1=an+ an+ 2 ? {an}是等差数列(3) an=kn+b ? {an}是等差数列 例3. 已知:lga,lgb,lgc与lga-lg2b,
lg2b-lg3c,lg3c-lga都是等差
数列,求a:b:c.例4.已知,三个数成等差数列,其和为15
首末两项的积为9,求此数列. 若三个数成等差数列,可设三个数为a-d,a,a+d若四个数成等差数列,可设四个数为a-3d,a-d,a+d,a+3d. 解: 因为b 是等差数列的中间一项,
所以2b=a+c=-1+7=6。
也就是b=3 a是-1和b的比例中项,所以2a =-1+b=2
所以a=1,
c是b和7的比例中项,所以2c=b+7=10
所以c=5.练习2.(1) 已知a,b,c成等差数列,求证:
ab-c2,ca-b2,bc-a2也成等差数列;
(2)三数成等差数列,它们的和为12,首尾二 数的积为12,求此三数. 6、4、2或2、4、6练习4.ABC的三内角成等差数列,三边成等比
数列,则三内角的公差为( )解: ∵ A+B+C=18002B=A+C,b2=ac∴ B=600, A+C=1200由正弦定理得:(sin600)2=sinAsinC故 A=B=C, 公差 d=0.练习5.已知{ an }为等比数列,则在下列数列中仍是等比
数列的是 .
①{2an}; ②{nan}; ③{|an|}; ④{an+an+1+an+2};
⑤{an·an+1}; ⑥{lgan}; ⑦{ }; ⑧{an+an+3+an+6}√√√√√√×× ① ③ ④ ⑤ ⑦ ⑧等差、等比数列的性质:(1)如果{an} 是等差数列,则{man}(其中m是常数)也是等差数列.(2)如果{an} 是等比数列,则{man}(其中m是非零常数)也是等比数列.(3)如果{an} 是等差数列,则{ank}(其中k是常数)也是等差数列.(4)如果{an} 是等差数列,则{ }(其中C,p,r是常数)是等比数列.(5)如果{bn}是等比数列,则{logapbnr}(其中a,p,r是常数,p?1)是等差数列.(6)在一个等差(或等比)数列中,等间隔地抽取其中的项组成一个新的数列,这个数列仍是等差数列。(7)如果{an} {bn}是等差数列,则{pan+ qbn }(其中p,q是常数)也是等差数列(9)如果{an} {bn}是等比数列,则{panm·qbnk}(其中p,q是非零常数,m,k是自然数)也是等比数列等差、等比数列的性质:例6.已知数列{an}与{bn}是等差数列,且cn= an+ bn (n=1,2,3,…)
求证:数列{cn}是等差数列.证明: 设等差数列{an}与{bn}的公差分别为d与d’,那么an+1-an=d , bn+1-bn=d’ (n=1,2,3,…),于是
cn+1-cn=( an+1+bn+1 ) - ( an+bn )=( an+1-an ) + ( bn+1 –bn )= d+d’根据等差数列的定义可知,数列{cn}是一个以d+d’为公差的等差数列.例7.已知数列{an}与{bn}是等比数列,且cn= an bn (n=1,2,3,…)
求证:数列{cn}是等比数列.证明: 设等比数列{an}与{bn}的公比分别为q与q’,那么an+1/an=q , bn+1/bn=q’ (n=1,2,3,…),于是
cn+1/cn=( an+1bn+1 ) /( anbn )= qq’根据等比数列的定义可知,数列{cn}是一个以qq’为公比的等比数列.1.练习册P21 18—23
2.练习册P27复习题1 -3—23
3.精练与博览P117(2)再见课后作业
证明:{pan+ qbn }(其中p,q是常数)也是等差数列(1)已知数列{ an }的通项公式是an =3n-1
求证:{an}为等差数列;(2) 已知数列{an}是等差数列,
求证:数列{an+an+1}也是等差数列.例1根据等比数列的定义可知,数列{kanmbn}是一个以qq’为公比的等比数列.(4).如果a,b,c成等差数列,而 a,c,b三数成等比数列,则a:b:c=________________ a,b,c成等差数列2b= a+cb= (a+c)/2
a,c,b成等比数列c2=ab①②①代入②,得:c2=a(a+c)/2解得: a=c或 a= -2c1:1:1或4:1:(-2)解:例2.已知数列的通项公式为an=pn+q
其中p,q是常数,且p≠0,那么
这个数列是否是等差数列?如果
是,其首项与公差是什么? 等差数列的判定方法:
(1) an+1-an=d ? {an}是等差数列(2) 2an+1=an+ an+ 2 ? {an}是等差数列(3) an=kn+b ? {an}是等差数列 例3. 已知:lga,lgb,lgc与lga-lg2b,
lg2b-lg3c,lg3c-lga都是等差
数列,求a:b:c.例4.已知,三个数成等差数列,其和为15
首末两项的积为9,求此数列. 若三个数成等差数列,可设三个数为a-d,a,a+d若四个数成等差数列,可设四个数为a-3d,a-d,a+d,a+3d. 解: 因为b 是等差数列的中间一项,
所以2b=a+c=-1+7=6。
也就是b=3 a是-1和b的比例中项,所以2a =-1+b=2
所以a=1,
c是b和7的比例中项,所以2c=b+7=10
所以c=5.练习2.(1) 已知a,b,c成等差数列,求证:
ab-c2,ca-b2,bc-a2也成等差数列;
(2)三数成等差数列,它们的和为12,首尾二 数的积为12,求此三数. 6、4、2或2、4、6练习4.ABC的三内角成等差数列,三边成等比
数列,则三内角的公差为( )解: ∵ A+B+C=18002B=A+C,b2=ac∴ B=600, A+C=1200由正弦定理得:(sin600)2=sinAsinC故 A=B=C, 公差 d=0.练习5.已知{ an }为等比数列,则在下列数列中仍是等比
数列的是 .
①{2an}; ②{nan}; ③{|an|}; ④{an+an+1+an+2};
⑤{an·an+1}; ⑥{lgan}; ⑦{ }; ⑧{an+an+3+an+6}√√√√√√×× ① ③ ④ ⑤ ⑦ ⑧等差、等比数列的性质:(1)如果{an} 是等差数列,则{man}(其中m是常数)也是等差数列.(2)如果{an} 是等比数列,则{man}(其中m是非零常数)也是等比数列.(3)如果{an} 是等差数列,则{ank}(其中k是常数)也是等差数列.(4)如果{an} 是等差数列,则{ }(其中C,p,r是常数)是等比数列.(5)如果{bn}是等比数列,则{logapbnr}(其中a,p,r是常数,p?1)是等差数列.(6)在一个等差(或等比)数列中,等间隔地抽取其中的项组成一个新的数列,这个数列仍是等差数列。(7)如果{an} {bn}是等差数列,则{pan+ qbn }(其中p,q是常数)也是等差数列(9)如果{an} {bn}是等比数列,则{panm·qbnk}(其中p,q是非零常数,m,k是自然数)也是等比数列等差、等比数列的性质:例6.已知数列{an}与{bn}是等差数列,且cn= an+ bn (n=1,2,3,…)
求证:数列{cn}是等差数列.证明: 设等差数列{an}与{bn}的公差分别为d与d’,那么an+1-an=d , bn+1-bn=d’ (n=1,2,3,…),于是
cn+1-cn=( an+1+bn+1 ) - ( an+bn )=( an+1-an ) + ( bn+1 –bn )= d+d’根据等差数列的定义可知,数列{cn}是一个以d+d’为公差的等差数列.例7.已知数列{an}与{bn}是等比数列,且cn= an bn (n=1,2,3,…)
求证:数列{cn}是等比数列.证明: 设等比数列{an}与{bn}的公比分别为q与q’,那么an+1/an=q , bn+1/bn=q’ (n=1,2,3,…),于是
cn+1/cn=( an+1bn+1 ) /( anbn )= qq’根据等比数列的定义可知,数列{cn}是一个以qq’为公比的等比数列.1.练习册P21 18—23
2.练习册P27复习题1 -3—23
3.精练与博览P117(2)再见课后作业
