不等式的基本性质
图片预览






文档简介
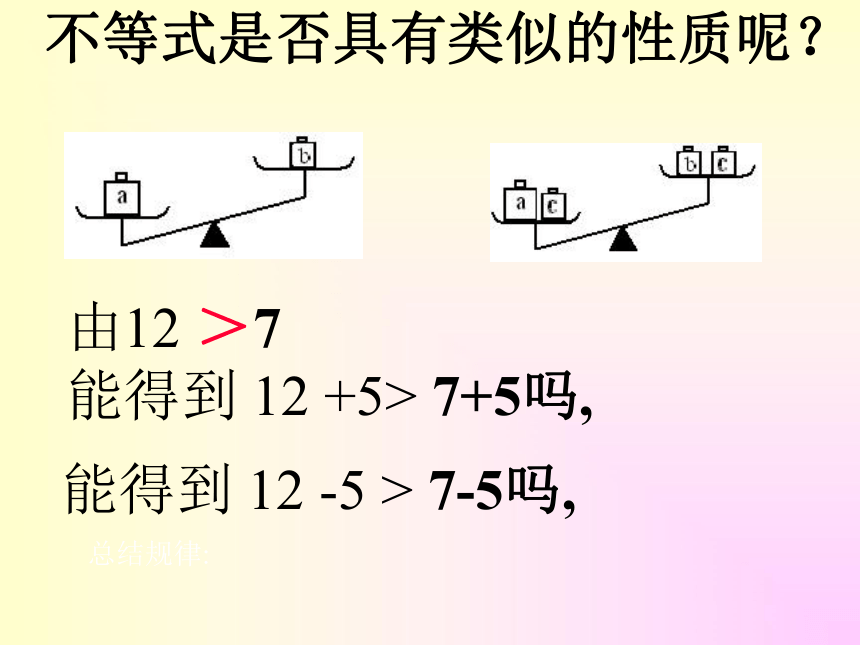
课件20张PPT。不等式的基本性质歙县小洲中心学校 方神州人教版七年级(下)由a+5=b+5, 能得到a=b吗?由0.5a=0.5b, 能得到a=b吗?由-5a=-5b, 能得到a=b?由a-5=b-5, 能得到a=b吗?等式基本性质1:等式的两边都加上(或减去)同一个整式,等式仍旧成立等式基本性质2:等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立如果 a=b,那么 a±c=b±c如果a=b,那么ac=bc,a÷c=b÷c(c≠0)符号表达式:符号表达式:不等式是否具有类似的性质呢?由12 >7能得到 12 +5> 7+5吗, 能得到 12 -5 > 7-5吗, 总结规律:观察:用“<”或“>”填空,并找一找其中的规律.(2) –1<3 , -1+2____3+2 , -1-3____3-3 ; (3) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ; (4) –2<3, (-2)×6____3×6 , (-2)×(-6)____3×(-6)5>3, 5+2____3+2 , 5-2____3-2 ;
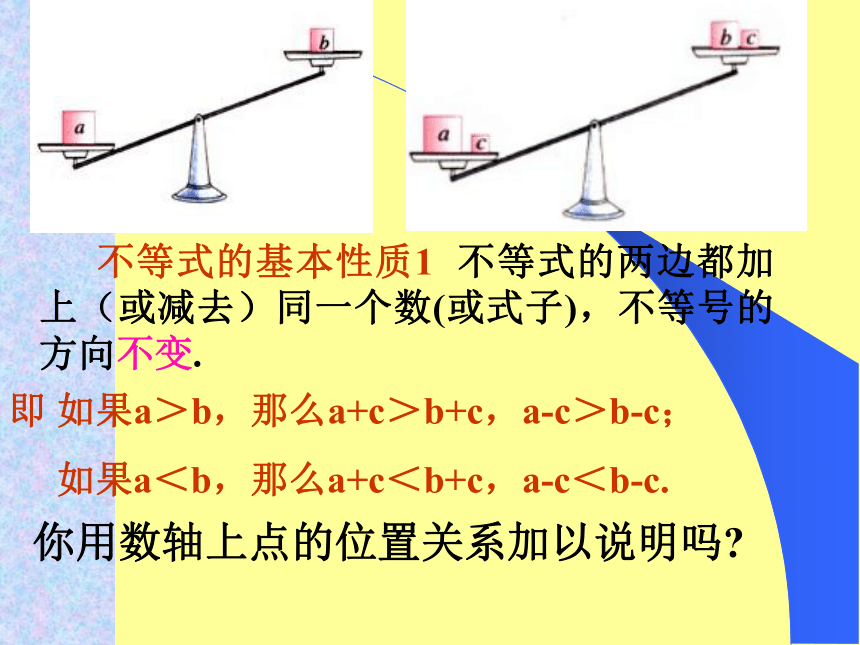
>><<><<>会发现:当不等式两边加或减去同一个数时,不等号的方向______不变 当不等式的两边同乘同一个正数时,不等号的方向______;而乘同一个负数时,不等号的方向________. 不变改变 不等式的基本性质1 不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变.
即 如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
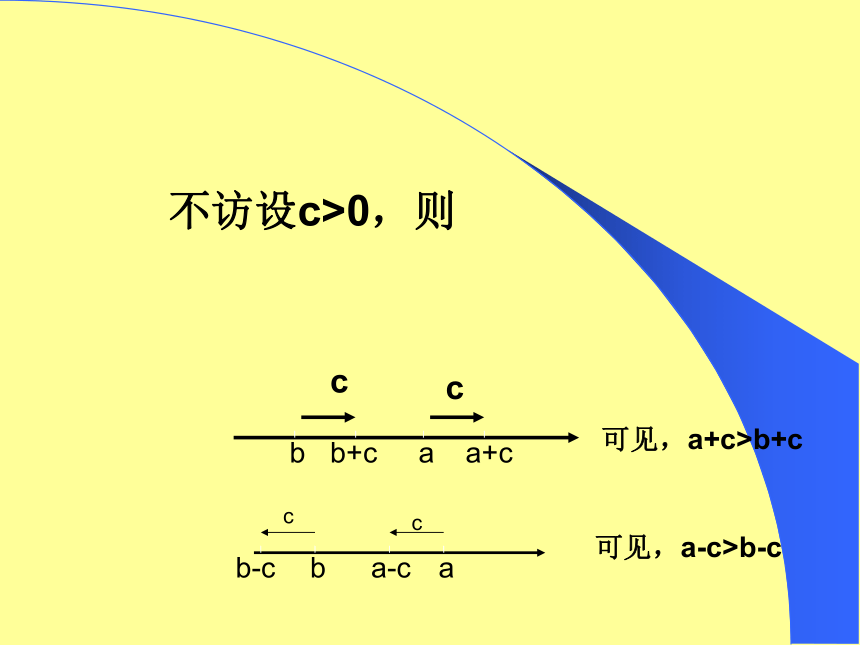
你用数轴上点的位置关系加以说明吗?不访设c>0,则abb+ca+ccc可见,a+c>b+cabb-ca-ccc可见,a-c>b-c练习:看谁填得又快又准确,并说出理由.(1)5<7,则5+4____7+4(2)-12<-4,则-12+a___-4+a(3)若a>b,则2a____a+b<<>探索:如果不等式的两边都乘以(或除以)同一个不 为0的数,不等号的方向是否也不变呢?7×3_____4×3
7×2_____4×2
7×1_____4×17×(-1)____4×(-1)
7×(-2)____4×(-2)
7×(-3)____4×(-3)上面两组式子反映的规律是什么?不等式基本性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。不等式基本性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。如果a<b,且c>0,那么ac<bc如果a>b,且c>0,那么ac>bc如果a<b,且c<0,那么ac>bc如果a>b,且c<0,那么ac<bc练习:若a>b,用不等号填空,并说出理由.(1)a-3____b-3(2)2a____2b(3)-a____-b>><做一做:选择适当的不等号填空:(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________<<≥≥x >-1不等式的基本性质2x >-3不等式的基本性质3X≥-2不等式的基本性质3例1:将下列不等式化成
X a或 x a的形式><(1) x-5 -1(2) -2x 3(3) 7x 6x -6>><等式与不等式的性质比较随堂练习:例 下列各题是否正确?请说明理由(1)如果a>b,那么ac>bc ( )(2)如果a>b,那么ac2 >bc2 ( )
(3)如果ac2>bc2,那么a>b ( )(4)如果x为实数,则4x >-3x ( )(5)如果ax>b且a≠0,那么x>b/a试一试1下列哪些是不等式x+3 > 6的解?哪些不是?
-4,-2. 5,0,1,2.5,3,3.2,4.8,8,12
判断
(1)∵a < b ∴ a-b < b-b
(2)∵a < b ∴ (3)∵a < b ∴ -2a < -2b
(4)∵-2a > 0 ∴ a > 0
(5)∵-a < 0 ∴ a < 3
3.填空
(1)∵ 2a > 3a ∴ a是 数
(2)∵ ∴ a是 数
(3)∵ax < a且 x > 1 ∴ a是 数
4.根据下列已知条件,说出a与b的不等关系,并说明是根据不等式哪一条性质。
(1)a-3 > b-3 (2) (3)-4a > -4b
5.直接想出不等式的解集,并在数轴上表示出来:
(1)x+3 > 6 (2)2x < 8
(3)x-2 > 0 (4)-4x-2 > x+3思考题:
某校学生步行参观,每小时走4千米,出发后2小时,情况发生变化,必须在60分钟内通知步行参观的队伍,学校派人骑自行车追赶大队,问每小时至少要骑多少千米?解 设骑车人的速度为x千米/小时,由题意有
(x-4)×1≥2 ×4解之得 x≥12答:每小时至少要骑12千米。热身练习在括号内填入“<”或“>”适当的符号:
23( )32
-62( )(-6)2
x+5( )x+3
0.9-x( )0.4-x<<>>把下列不等式化为x>a或x (1) 2x>x+3; (2) 3x-1<40+2x;
(3) 4(x+3)>3(x+4); (4) 2(x-3)
>><<><<>会发现:当不等式两边加或减去同一个数时,不等号的方向______不变 当不等式的两边同乘同一个正数时,不等号的方向______;而乘同一个负数时,不等号的方向________. 不变改变 不等式的基本性质1 不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变.
即 如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
你用数轴上点的位置关系加以说明吗?不访设c>0,则abb+ca+ccc可见,a+c>b+cabb-ca-ccc可见,a-c>b-c练习:看谁填得又快又准确,并说出理由.(1)5<7,则5+4____7+4(2)-12<-4,则-12+a___-4+a(3)若a>b,则2a____a+b<<>探索:如果不等式的两边都乘以(或除以)同一个不 为0的数,不等号的方向是否也不变呢?7×3_____4×3
7×2_____4×2
7×1_____4×17×(-1)____4×(-1)
7×(-2)____4×(-2)
7×(-3)____4×(-3)上面两组式子反映的规律是什么?不等式基本性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。不等式基本性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。如果a<b,且c>0,那么ac<bc如果a>b,且c>0,那么ac>bc如果a<b,且c<0,那么ac>bc如果a>b,且c<0,那么ac<bc练习:若a>b,用不等号填空,并说出理由.(1)a-3____b-3(2)2a____2b(3)-a____-b>><做一做:选择适当的不等号填空:(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________<<≥≥x >-1不等式的基本性质2x >-3不等式的基本性质3X≥-2不等式的基本性质3例1:将下列不等式化成
X a或 x a的形式><(1) x-5 -1(2) -2x 3(3) 7x 6x -6>><等式与不等式的性质比较随堂练习:例 下列各题是否正确?请说明理由(1)如果a>b,那么ac>bc ( )(2)如果a>b,那么ac2 >bc2 ( )
(3)如果ac2>bc2,那么a>b ( )(4)如果x为实数,则4x >-3x ( )(5)如果ax>b且a≠0,那么x>b/a试一试1下列哪些是不等式x+3 > 6的解?哪些不是?
-4,-2. 5,0,1,2.5,3,3.2,4.8,8,12
判断
(1)∵a < b ∴ a-b < b-b
(2)∵a < b ∴ (3)∵a < b ∴ -2a < -2b
(4)∵-2a > 0 ∴ a > 0
(5)∵-a < 0 ∴ a < 3
3.填空
(1)∵ 2a > 3a ∴ a是 数
(2)∵ ∴ a是 数
(3)∵ax < a且 x > 1 ∴ a是 数
4.根据下列已知条件,说出a与b的不等关系,并说明是根据不等式哪一条性质。
(1)a-3 > b-3 (2) (3)-4a > -4b
5.直接想出不等式的解集,并在数轴上表示出来:
(1)x+3 > 6 (2)2x < 8
(3)x-2 > 0 (4)-4x-2 > x+3思考题:
某校学生步行参观,每小时走4千米,出发后2小时,情况发生变化,必须在60分钟内通知步行参观的队伍,学校派人骑自行车追赶大队,问每小时至少要骑多少千米?解 设骑车人的速度为x千米/小时,由题意有
(x-4)×1≥2 ×4解之得 x≥12答:每小时至少要骑12千米。热身练习在括号内填入“<”或“>”适当的符号:
23( )32
-62( )(-6)2
x+5( )x+3
0.9-x( )0.4-x<<>>把下列不等式化为x>a或x
(3) 4(x+3)>3(x+4); (4) 2(x-3)
