2008中考数学模拟试题

2008年中考数学模拟卷
题 号
一
二
三
四
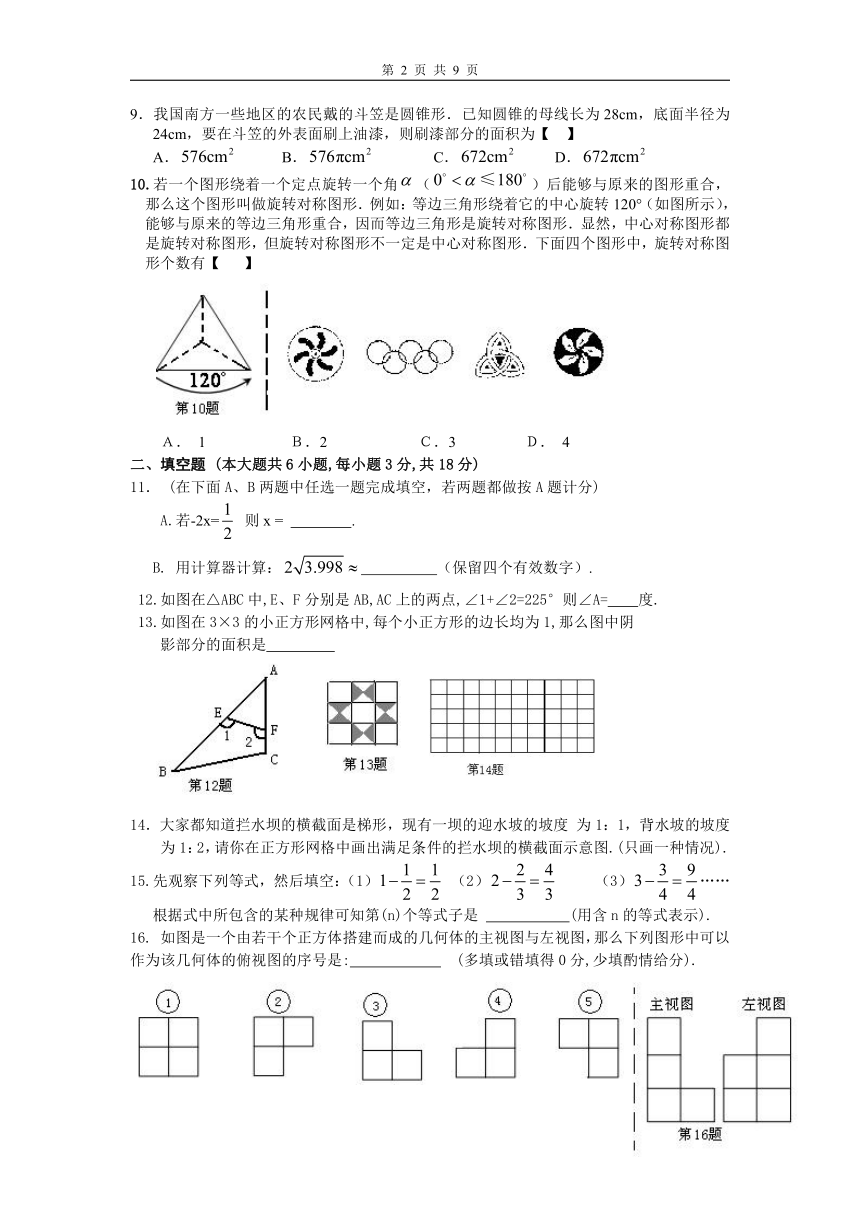
五
六
总 分
得 分
说明：本卷共有六个大题，25个小题，全卷满分120分，考试时间120分钟.
一、选择题（本大题共10小题，每小题3分，共30分）
1.下列计算正确的是【 】
A. -2-2=0 B. =0 C. 3÷=1 D.=10
2.2008年元月我国南方遭受暴雪冰冻灾害，国家给予某地区821万元救灾，这个数用科学记数法表示为【 】元.
A. B. C. D.
3. 下列计算正确的是【 】
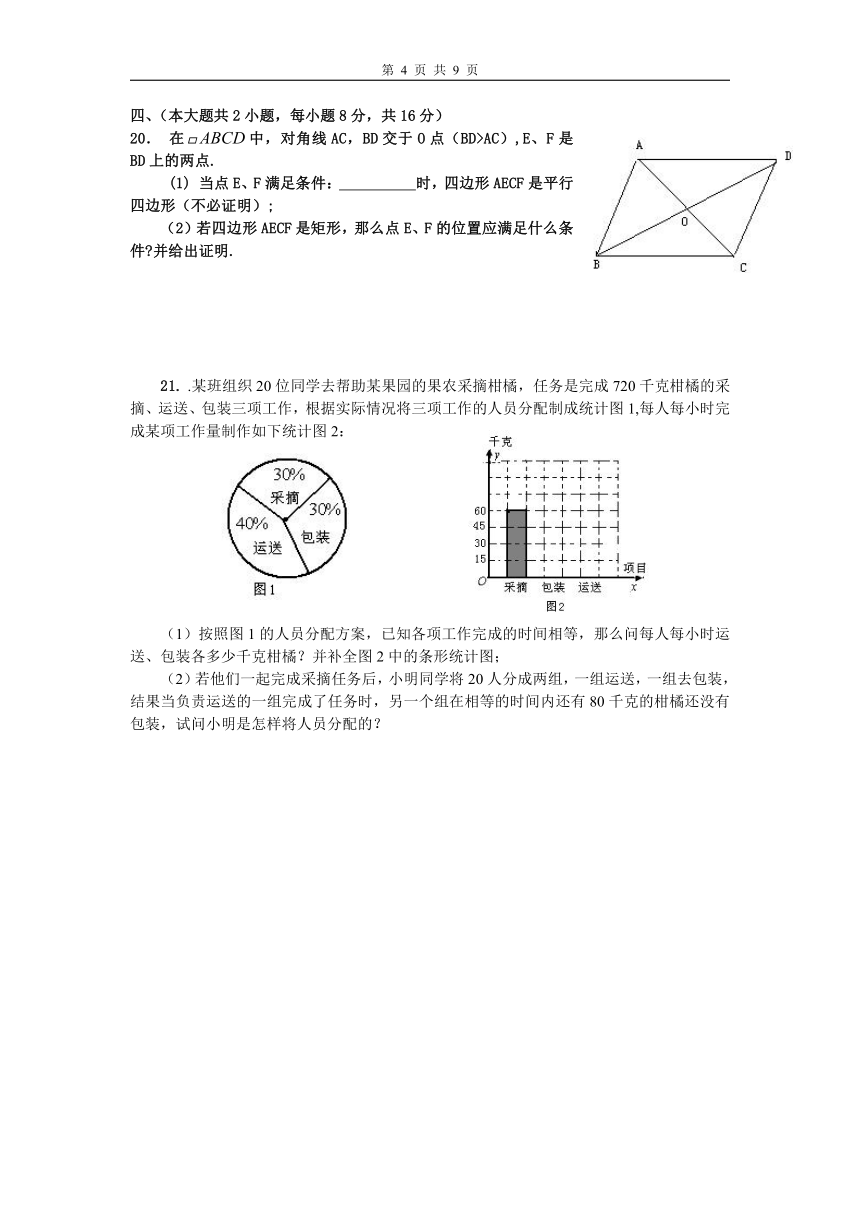
A．， B. ， C.，D.=
4.如图,右边整个图案可以由【 】平移得到.
5. 某学校有1000名九年级学生,要知道他们在学业水平考试中成绩为A等、B等、C等、
D 等的人数各是多少，需要做的工作是【 】
A．求平均成绩 B. 进行频数分布 C. 求极差 D.计算方差
6. 太阳光透过一个矩形玻璃窗户，照射在地面上，
影子的形状不可能是【 】
A.等腰梯形 B.平行四边形 C.矩形 D.正方形
7. 已知：如图，，，以为位似中心，
按位似比为把缩小，则点F的对应点F′的坐标
为【 】
A． B．(-8,-4)或(8,4)
C．或(2,1) D．
8.如图：将一个矩形纸片ABCD，沿着BE折叠，使C、D点分别落
在点 处.若，则的度数为【 】
A． B. C. D.
9．我国南方一些地区的农民戴的斗笠是圆锥形．已知圆锥的母线长为28cm，底面半径为24cm，要在斗笠的外表面刷上油漆，则刷漆部分的面积为【 】
A． B． C． D．
10.若一个图形绕着一个定点旋转一个角（）后能够与原来的图形重合，那么这个图形叫做旋转对称图形．例如：等边三角形绕着它的中心旋转120°（如图所示），能够与原来的等边三角形重合，因而等边三角形是旋转对称图形．显然，中心对称图形都是旋转对称图形，但旋转对称图形不一定是中心对称图形．下面四个图形中，旋转对称图形个数有【 】
Ａ． 1 Ｂ．2 Ｃ．3 Ｄ． 4
二、填空题 (本大题共6小题,每小题3分,共18分)
11． (在下面A、B两题中任选一题完成填空，若两题都做按A题计分)
A.若-2x= 则x = .
B. 用计算器计算： （保留四个有效数字）.
12.如图在△ABC中,E、F分别是AB,AC上的两点,∠1+∠2=225°则∠A= 度.
13.如图在3×3的小正方形网格中,每个小正方形的边长均为1,那么图中阴
影部分的面积是

14．大家都知道拦水坝的横截面是梯形，现有一坝的迎水坡的坡度 为1：1，背水坡的坡度为1：2，请你在正方形网格中画出满足条件的拦水坝的横截面示意图.(只画一种情况).
15.先观察下列等式，然后填空：（1） （2） （3）……根据式中所包含的某种规律可知第(n)个等式子是 (用含n的等式表示).
16. 如图是一个由若干个正方体搭建而成的几何体的主视图与左视图，那么下列图形中可以作为该几何体的俯视图的序号是: (多填或错填得0分,少填酌情给分).
三、(本大题共3小题,第17题6分，第18、19均为7分，共20分）.
17.化简:
18．售价为210元的商品，其利润率若要保证不小于40﹪且不大于50﹪，那么这种商品的进价应在什么范围内？
19．小明有红、黄、白、黑四件衬衫，又有黑色、蓝色、灰色三条长裤.如果他喜欢穿白色衬衫和黑色长裤，那么他在黑暗中随机摸出一套衣裤正是他喜欢的搭配，这种巧合发生的概率是多少？并用列表或树状图说明理由.
四、（本大题共2小题，每小题8分，共16分）
20． 在中，对角线AC，BD交于O点（BD>AC）,E、F是BD上的两点.
(1) 当点E、F满足条件： 时，四边形AECF是平行四边形（不必证明）;
（2）若四边形AECF是矩形，那么点E、F的位置应满足什么条件?并给出证明.
21. .某班组织20位同学去帮助某果园的果农采摘柑橘，任务是完成720千克柑橘的采摘、运送、包装三项工作，根据实际情况将三项工作的人员分配制成统计图1,每人每小时完成某项工作量制作如下统计图2：
（1）按照图1的人员分配方案，已知各项工作完成的时间相等，那么问每人每小时运送、包装各多少千克柑橘？并补全图2中的条形统计图；
（2）若他们一起完成采摘任务后，小明同学将20人分成两组，一组运送，一组去包装，结果当负责运送的一组完成了任务时，另一个组在相等的时间内还有80千克的柑橘还没有包装，试问小明是怎样将人员分配的？
五、（本大题共2小题，第22题8分，第23题9分，共17分）
22. 如图,AB是⊙O的直径,且AB=10,直线CD交⊙O于C、D.交AB于E.OP⊥CD于P，
∠PEO=45°OP=.
求线段CD的长；
（2）试问将直线CD通过怎样的变换才能与⊙O切于B或A.
23. （1）如图1，在中，绕点C旋转后，得到请先画出变换后的图形写出下列结论正确的序号是 .
① ②线段AB绕C点旋转后，得到线段
③//AB ④C是线段的中点
在（1）的启发下解答下面问题：
（2）如图2，在中，，D是BC的中点，射线DF交BA于E，交CA的延长线于F，请猜想等于多少度时，BE=CF（直接写出结果，不证明），
（3）如图3，在中，如果，而（2）中的其他条件不变，若BE=CF的结论仍然成立，那么与满足什么数量关系（等式表示）？并加以证明.
六、（本大题共2小题，第24题9分，第25题10分，共19分）
24．小敏妈一天共带了若干元钱去商店买糖果,当她买了甲种糖果后,又去购买乙种糖果,于是她手中持有的钱数(元)与购买糖果千克数之间的函数关系如图所示.
请结合图象,回答下列问题:
(1)根据图象中的信息,请你写出一个正确结论;
(2)当她购买甲种糖果4千克后,再购买了多少千克的乙种糖果刚好用完106元?
(3)小敏根据两种糖果的价格说:“共购10.6千克糖果,妈妈手中所持有的钱会刚好用完”,问小敏是怎样打算购买这两种糖果的?请说明理由.
25.如图，四边形ABCD是边长为4的正方形，动点P、Q同时从A点出发，点P沿AB以每秒1个单位长度的速度向终点B运动.点Q沿折线ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒.
(1)当t=2秒时,求证PQ=CP.
(2)当2（3）设的面积为S，那么S 与t之间的函数关系如何？并问S的值能否大于正方形ABCD面积的一半？为什么？
参考答案
1．B，2．D，3．D，4．A，5．B，6.A，7.C，8.B，9.D，10，C.
11．A．，B.3.999，12.45，13.2，14.
15．
16．①②③
17.解: 原式= ...........4分
=3..................................................6分
18．解： 设这种商品进价为m元, 根据题意可得：
(1+50﹪)m≥210≥(1+40﹪)m..................4分
140≤m≤i50........................7分
19．解：..................................4分
其中，黑裤配白色的衬衫仅仅是12种中的一种………………7分
20. （1）BE=DF或OE=OF，…………………………………… 3分
（2）OE=OF=OA或OE=OF=OC或OE=OF且AC=EF，…………4分
略证:因为OA=OE=OF=OC则,EF=AC 所以四边形A ECF是矩形………8分
21．解：（1）采摘 运送 包装
设采摘了x小时，则 360x=720 x=2(小时)
每人每时包装（千克）
每人每时运送（千克）………………….4分
（2）负责运送的人数为y，则包装人数为20-y ，
y=12 20-12=8(人)………………………7分
检验:(略)
答：(1)运送每人每小时45千克，包装每人每小时60千克，(2)小明安排了12人运送，8人包装…………………………………………………8分
22．解：（1）如图1,连结OC，∵OP⊥CD
∴CP=1/2CD= ，∴CD=2...................4分
（2）∵∠PEO=45°，OE=2，BE=3，
∴将直线CD绕着点E逆时针旋转45°后,若再沿射线EB平移3个单位,直线CD与⊙O相切于B,或再沿射线EA平移7个单位,直线CD与⊙O相切于A (如图2) .........8分
23．解：（1） ①②③④ ……………………4分
（2） ............................6分
（3）等量关系，.作关于点D的中心对称三角形，则，，=∠BED=∠FEA
∴.........................9分
24．解:(1)如:小敏妈手中共持有120元,甲、乙两种糖果每千克分别为10元、12元，当甲种糖果购买4千克后，小敏妈手中还余80元钱
…………2分
(2)当＞4时,设函数解析式为
………4分
当=120-106=14 14=-12+128 =9.5
9.5-4=5.5
再购买了5.5千克乙种糖果刚好用完106元………………………6分
(3)甲、乙两种的价格分别是每千克10元、12元.
设甲、乙两种糖果各买x,y千克。

小敏打算先购买甲种糖果3.6千克,再购买乙种糖果7千克,刚好用完120元…………9分
25.（1）当t=2时，（如图1），Q与D重合，P恰好是AB的中点，，
则PQ=CP……………………3分
（2）当2（3）当0≤t≤2时，（如图3），
……………7分
当2 又开口向下对称轴为t=3,
∴0≤t≤2时，S随t增大而增大，当t=2时，S取得最大值为8.又 ∵S=-4t+16,
2.