2023年高中信息技术 分治算法 课件(共76张PPT)
文档属性
| 名称 | 2023年高中信息技术 分治算法 课件(共76张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 420.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2023-11-17 13:05:22 | ||
图片预览







文档简介
(共76张PPT)
分治算法
2023年高中信息技术教学课件
主要内容
1.分治思想
2.经典问题
3.基于一维的分治
4.基于二维的分治
5.点分治
分治思想
分治(Divide-And-Conquer)就是“分而治之”的意思,其实质就是将原问题分成n个规模较小而结构与原问题相似的子问题;然后递归地解这些子问题,最后合并其结果就得到原问题的解。
其三个步骤如下:
①划分问题(Divide):将原问题分成一系列子问题。
②递归解决(Conquer):递归地解各子问题。若子问题足够小,则可直接求解。
③合并问题(Combine):将子问题的结果合并成原问题的解。
如快速排序、归并排序等都是采用分治思想。
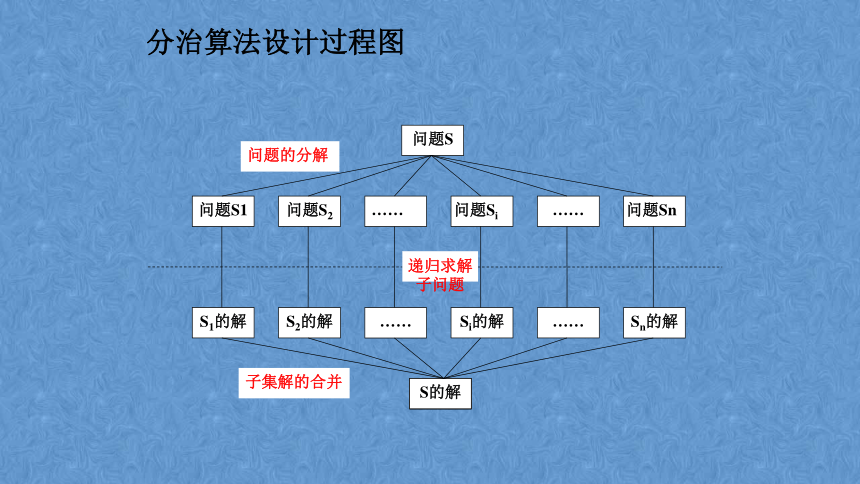
分治算法设计过程图
问题S
问题S
问题S
S的解
问题S1
……
问题S2
问题Si
问题Sn
……
S1的解
……
S2的解
Si的解
Sn的解
……
问题的分解
子集解的合并
递归求解子问题
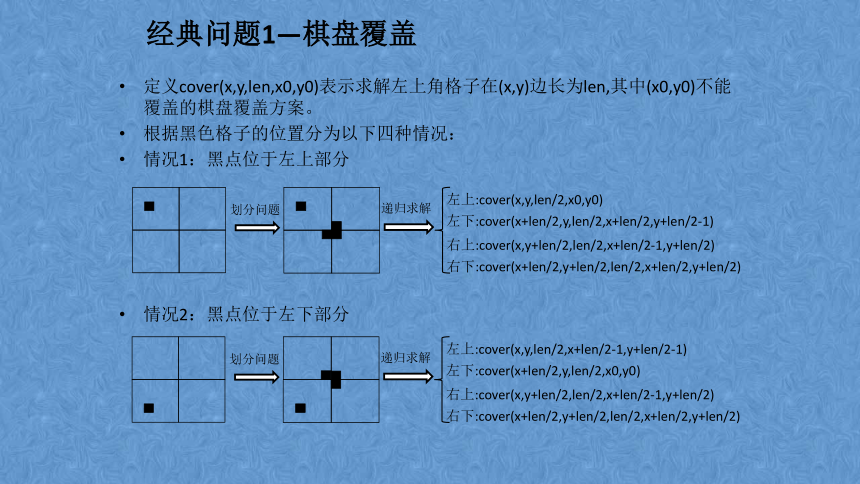
经典问题1—棋盘覆盖
有一个2k*2k的方格棋盘,恰有一个方格是黑色的,其他为白色。你的任务是用包含3个方格的L型牌覆盖所有白色方格。黑色方格不能被覆盖,且任意一个白色方格不能同时被两个或更多牌覆盖。如下图所示为L型牌的4种旋转方式。
经典问题1—棋盘覆盖
题目是要求用L型牌覆盖一个2k*2k的方格棋盘,棋盘有且只有一个黑色方格,且此方格不能被覆盖。
用分治来解决,把原棋盘平均分为4块,通过用1个L型牌覆盖棋盘正中间2*2的区域中的三个格子,把原棋盘分成4块2k-1*2k-1的方格棋盘,且每块中只含有一个黑色方格(不能覆盖的格子)。
此时把原问题分解成4个结构与原问题一样的子问题,棋盘的大小(边长)每次减半,最终会出现边长为1的情况,直接求解即可。
经典问题1—棋盘覆盖
定义cover(x,y,len,x0,y0)表示求解左上角格子在(x,y)边长为len,其中(x0,y0)不能覆盖的棋盘覆盖方案。
根据黑色格子的位置分为以下四种情况:
情况1:黑点位于左上部分
情况2:黑点位于左下部分
递归求解
划分问题
左上:cover(x,y,len/2,x0,y0)
左下:cover(x+len/2,y,len/2,x+len/2,y+len/2-1)
右上:cover(x,y+len/2,len/2,x+len/2-1,y+len/2)
右下:cover(x+len/2,y+len/2,len/2,x+len/2,y+len/2)
递归求解
划分问题
左上:cover(x,y,len/2,x+len/2-1,y+len/2-1)
左下:cover(x+len/2,y,len/2,x0,y0)
右上:cover(x,y+len/2,len/2,x+len/2-1,y+len/2)
右下:cover(x+len/2,y+len/2,len/2,x+len/2,y+len/2)
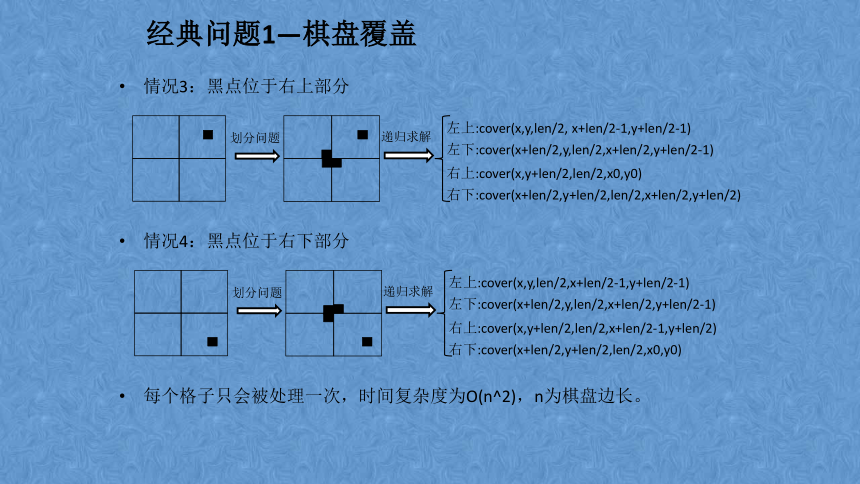
经典问题1—棋盘覆盖
情况3:黑点位于右上部分
情况4:黑点位于右下部分
每个格子只会被处理一次,时间复杂度为O(n^2),n为棋盘边长。
递归求解
划分问题
左上:cover(x,y,len/2, x+len/2-1,y+len/2-1)
左下:cover(x+len/2,y,len/2,x+len/2,y+len/2-1)
右上:cover(x,y+len/2,len/2,x0,y0)
右下:cover(x+len/2,y+len/2,len/2,x+len/2,y+len/2)
递归求解
划分问题
左上:cover(x,y,len/2,x+len/2-1,y+len/2-1)
左下:cover(x+len/2,y,len/2,x+len/2,y+len/2-1)
右上:cover(x,y+len/2,len/2,x+len/2-1,y+len/2)
右下:cover(x+len/2,y+len/2,len/2,x0,y0)
经典问题1—棋盘覆盖—代码
void cover(int x,int y,int len,int x0,int y0)
{
int t,len1;
if (len==1)return;
t=++tot;
len1=len/2;
if (x0else{board[x+len1-1][y+len1-1]=t;cover(x,y,len1,x0+len1-1,y0+len1-1);}
if (x0>=x+len1&&y0else{board[x+len1][y+len1-1]=t;cover(x+len1,y,len1,x+len1,y+len1-1);}
if (x0=y+len1)cover(x,y+len1,len1,x0,y0);
else{board[x+len1-1][y+len1]=t;cover(x,y+len1,len,x+len1-1,y+len1);}
if (x0>=x+len1&&y0>=y+len1)cover(x+len1,y+len1,len1,x0,y0);
else{board[x+len1][y+len1]=t;cover(x+len1,y+len1,len1,x+len1,y+len1);}
}
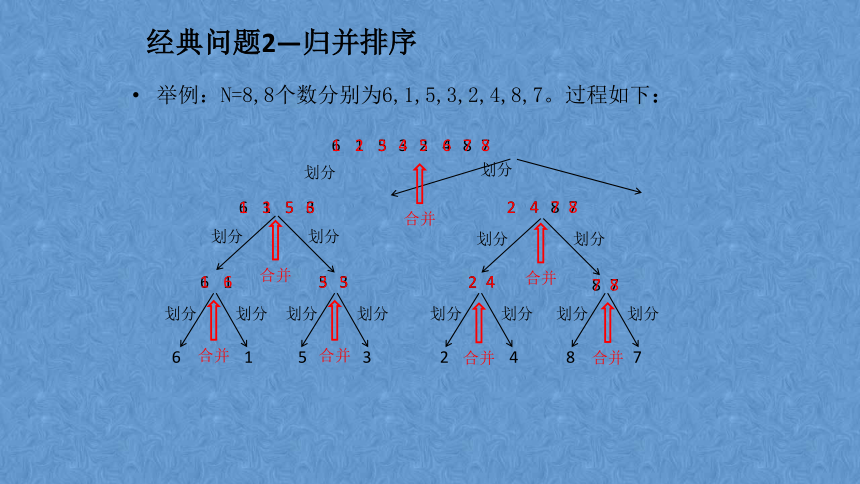
经典问题2—归并排序
给定一个长度为N的序列,对其进行排序。
归并排序思想:
1.划分问题:把长度为N的序列尽可能均分成左右两部分;
2.递归求解:对左右两部分分别进行归并排序;
3.合并问题:把左右两段排好序的序列合并出最终的有序序列。
经典问题2—归并排序
举例:N=8,8个数分别为6,1,5,3,2,4,8,7。过程如下:
6
5
1
3
4
2
7
8
6
5
1
3
4
2
7
8
6
1
5
3
4
2
7
8
6
1
5
3
2
4
8
7
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
合并
合并
合并
合并
合并
合并
合并
1
3
2
4
6
5
8
7
1
5
3
6
4
2
8
7
1
6
3
5
4
2
8
7
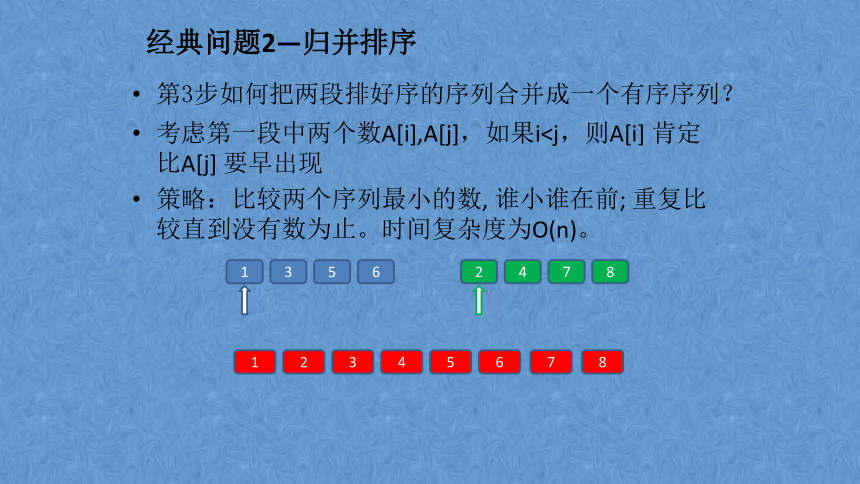
经典问题2—归并排序
第3步如何把两段排好序的序列合并成一个有序序列?
考虑第一段中两个数A[i],A[j],如果i策略:比较两个序列最小的数, 谁小谁在前; 重复比较直到没有数为止。时间复杂度为O(n)。
1
3
5
6
2
4
7
8
1
2
3
4
5
6
7
8
经典问题2—归并排序—代码
void merge(l,m,r)// 合并操作
{
// i 代表左半序列目前最小的位置
// j 代表右半序列目前最小的位置
// a:原数组b 数组:暂存数组(合并过程不能覆盖原数组)
int i = l, j = m+1, k = l;
for(; i<=m && j<=r; )
if(a[i] <= a[j]) b[k++] = a[i++]; // 加入左边最小的
else b[k++] = a[j++]; // 加入右边最小的
// 加入剩余的数
for(; i<=m; b[k++] = a[i++]); // 加入剩余左半的数
for(; j<=r; b[k++] = a[j++]); // 加入剩余右半的数
for(i=l; i<=r; i++) a[i] = b[i]; // 从暂存数组中赋值
}
经典问题2—归并排序—代码
void merge_sort(int l, int r) // 排序位置从l 到r 的序列
{
if(l==r) return; // 长度为1 则不需要排序
int m = (l+r) / 2; // 分成两段
merge_sort(l, m); // 排序左半段
merge_sort(m+1, r); // 排序右半段
merge(l,m,r);//把两段排好序的序列合并成一个有序序列
}
经典问题2—归并排序—时间复杂度分析一
F(n)表示对n个数进行归并排序的时间复杂度
根据归并排序思想有:
F(n)=2*F(n/2)+n
设n’=2^k,k=lgn’,则有:
F(n’)=2*F(n’/2)+n’=2*(2*F(n’/4)+n’/2)+n’=4*F(n’/4)+2*n’
=4*(2*F(n’/8)+n’/4)+2*n’=8*F(n’/8)+3*n’
=……=2^k*F(1)+k*n’=2^k+k*2^k=n’+n’*lgn’
设n’<=n<2*n’,则有F(n’)<=F(n)n’+n’lgn’<=F(n)<=2*n’+2*n’*lg(2*n’)
n’+n’lgn’<=F(n)<=2*n’+2*n’*lg2+2*n’*lgn’
所以F(n)=O(nlgn)。
经典问题2—归并排序—时间复杂度分析二
画出归并排序的递归树。
时间主要花费在合并上,每一层合并代价综合为n,树的深度为lgn,所以时间复杂度为O(nlgn)。
n
n/2
n/2
n/4
n/4
n/4
n/4
1
1
1
1
1
1
1
1
n
n
n
n
lgn
经典问题3—逆序对统计
给定一个长度为N 的序列,定义它的逆序对数为;
二元组(i,j),满足iA[j]。要求统计逆序对数。
例如:对于A=[3 2 5 1 4],逆序对数为5:3>2, 3>1, 2>1,5>1, 5>4。
经典问题3—逆序对统计
下面介绍一种使用归并排序计算逆序对的方法(利用分治算法的思想) 。
长度为N 的序列的逆序对数ans 可以分为3部分:
① 左半段的逆序对数L_ans
②右半段的逆序对数R_ans
③(i,j)分立两侧的逆序对数C_ans
* 结论:ans = L_ans + R_ans + C_ans
例如:对于A=[3 2 5 1 4],分成两段A1 = [3 2 5], A2 = [1 4]
L_ans= 1(3>2), R_ans = 0, C_ans = 4(3>1, 2>1, 5>1, 5>4)
ai
aj
ai
aj
ai
aj
经典问题3—逆序对统计
ans = L_ans + R_ans + C_ans
其中L_ans,R_ans是与计算ans相同类型的子问题,递归计算即可。主要考虑(i,j)分立两侧的逆序对数C_ans:
结论:对两半段的数分别排序, (i 在左半段,j 在右半段,排在不同位置不影响先后关系) ,C_ans 不变
例如:对于A=[3 2 5 1 4],分成两段A1 = [3 2 5], A2 = [1 4],对A1 和A2 进行排序,A’ = [2 3 5 1 4], C_ans 仍然为4(3>1,2>1, 5>1, 5>4)
经典问题3—逆序对统计
考虑(i,j)分立两侧的逆序对数C_ans:
考虑在合并过程中,统计它们的分立两侧逆序对总数:
左部分区间为[L,m],右部分[m+1,r],在合并过程中,左右指针分别为i,j,当出现A[i]>A[j]时,(i,j)是一个逆序对,且A[L..m]是升序,所以(i+1,j),(i+2,j)…(m,j)也都是逆序对,答案ans可以直接增加m-i+1。
经典问题3—逆序对统计
如N=8,序列为[6,1,5,3,2,4,8,7],分成[6,1,5,3],[2,4,8,7]左右两段, 递归计算出L_ans=4,R_ans=1,两部分排好序分别为[1,3,5,6],[2,4,7,8],C_ans的计算如下:
1
3
5
6
2
4
7
8
1
2
3
4
5
6
7
8
C_ans=
0
+3=3
+2=5
经典问题3—逆序对统计—代码
可以直接套用归并排序的模板,在合并过程顺便统计逆序对数。对于合并程序稍作改变。
void merge(l,m,r)// 合并操作,同时统计逆序对
{
int i = l, j = m+1, k = l;
for(; i<=m && j<=r; )
if(a[i] <= a[j]) b[k++] = a[i++]; // 加入左边最小的
else ans += m-i+1,b[k++] = a[j++];
// 插入右半段的时候,逆序对数增加
for(; i<=m; b[k++] = a[i++]); // 加入剩余左半的数
for(; j<=r; b[k++] = a[j++]); // 加入剩余右半的数
for(i=l; i<=r; i++) a[i] = b[i]; // 从暂存数组中赋值
}
经典问题4—最近点对问题
给定平面上n(n>=2)个点,计算最近点对的距离。距离指欧几里得距离。即点p1(x1,y1)和p2(x2,y2)之间的距离为。可能有点重合,在这种情况下,它们之间的距离为0。这一问题可以应用于交通控制等系统中,在空中或海洋交通控制系统中,需要发现两个距离最近的交通工具,以便检测出可能发生的相撞事故。
经典问题4—最近点对问题
方法一:暴力枚举
共C(n,2)=n*(n-1)/2个点对,时间复杂度为O(n^2)。
经典问题4—最近点对问题
方法二:考虑用分治
ans表示n个点的最近点对距离,先判重,如有点重合ans=0。
否则把n个点尽可能均分为左右两部分,ans的值只有以下3种情况:
1.左边部分的最近点对距离d1
2.右边部分的最近点对距离d2
3.左半部分的点与右半部分点形成的最小距离d3
ans=min(min(d1,d2),d3)
左右两部分的最近点对问题是与原问题结构性质一样的子问题,可以递归求解出d1,d2
第3部分d3的求解是问题的关键。
经典问题4—最近点对问题
分治法的时间复杂度T(n)=2*T(n/2)+D(n),其中D(n)表示计算d3的时间复杂度。
如果d3的计算采用普通枚举法,两两枚举左右两部分的点对,则D(n)=n*n/4
设n=2^k
T(n)=2*T(n/2)+n*n/4
=2*(2*T(n/4)+n*n/16)+n*n/4
=4*T(n/4)+n*n/8+n*n/4
=8*T(n/8)+n*n/16+n*n/8+n*n/4
=…=2^k*T(1)+n^2/4+n^2/8+…+n^2/(2^(k+1))
=(n^2+n)/2=O(n^2)
并没有比暴力枚举快多少。
经典问题4—最近点对问题
如果D(n)=c*n,则T(n)=2*T(n/2)+c*n=O(nlgn)
D(n)=c*n,说明计算d1,d2,d3时不能采用排序。做法如下:
1.前期准备:一开始,把输入的n个点复制到A和B数组中,对A数组按x坐标单调递增的顺序排序,对B数组按y坐标单调递增的顺序排序,并建立映射Index[],Index[i]表示B数组第i个点在A数组的第Index[i]位置,即B[i]与A[Index[i]]是同一个点。接下来进行判重,如有点重合,则返回答案为0。否则进入第二步开始递归
2.算法的每一次递归调用的输入都是点集对应的数组A和B,如果点数n<=3,则直接暴力枚举。如n>3则:
经典问题4—最近点对问题
①划分问题:直接用数组A的中间位置m作为分界点,A数组中m左侧(含m)的点为左半部分的点,m右侧的点为右半部分的点,数组A很容易就被划分为AL和AR ,从左到右扫描B中的点,判断Index[i]与m的大小关系,如Index[i]<=m,则该点属于BL否则属于BR,同时更新BL和BR对应的Index[]。时间复杂度为O(n)
②递归解决:递归求解出左右两部分的最近点对距离d1,d2,取较小值d=min(d1,d2)
经典问题4—最近点对问题
③合并问题:答案ans=min(d,d3),d3表示左半部分的点到右半部分点的最短距离,如果存在点对使得d3为了找出这样的点对(如果存在的话),算法需要做如下工作:
经典问题4—最近点对问题
1)建立数组B’,它是把数组B中所有不在宽度为2d的垂直带形区域内的点去掉后得到的数组,所以B’也是按y坐标顺序排序的。
2)从左到右扫描B’中的每一个点p,尝试找出后面与p距离小于d的点。下面将会看到,仅需考虑紧随p后面的6个点,并记录下B’中所有点对的最小距离d3。
3)如果d3这样一来,合并问题的时间复杂度为O(n),总时间复杂度可以做到O(nlgn)。
经典问题4—最近点对问题
正确性
枚举宽度为2d的带形区域中的一点p,考虑其后面的点p’
如果dis(p,p’)d
d
d
p
经典问题4—最近点对问题
正确性
观察属于左半部分的d*d的正方形区域,如该区域内的点全部属于左半部分,通过横向纵向两条直线把d*d的正方形区域均分为4个d/2*2/2的小正方形,因为每个小正方形最远的两个点的距离为对角线即sqrt(2)*d/2同理属于右半区域的最多也只有4个点,所以整个2d*d区域内最多只有8个点。
经典问题4—最近点对问题
正确性
再仔细分析,如果有8个点,则一定有两对点是重合的,而算法一开始就已经排除了重复。
那是不是就一共只有6个点,只需判断后面的5个点呢?
下面如图所示是7个点的情况,所以最多是7个点,只需判断后面的6个点。
经典问题4—最近点对问题
算法导论中不严谨之处?
算法导论指出:只需考虑p后面的7个点,因为2d*d区域因为重合点最多有8个点。
问题是:如果有重合点可能就不是2个点重合,可能是3个,4个甚至更多。
当然:算法导论的做法不影响结果,因为如果更多的点重合,在递归时就已经算出d=0,后面判断7个点不影响结果,如果没有点重合,只需判断6个点,那么判断7个点也不影响正确性。
即使你不清楚上面的性质,但一开始进行了判重,且在枚举p’时增加了纵坐标相差不超过d的判断,一样可以在O(nlgn),因为你无形之中用了上面的性质。
一维分治1:CF429D Tricky Function
给出一个长度为N的序列a。
定义
求最小的f(i,j)
N ≤ 100000
Time Limit: 2s
一维分治1:CF429D Tricky Function
设Sum[i]表示a[1]+a[2]+…+a[i]
那么g(i,j)=Sum[j]-Sum[i]
问题变成:求形如( i , Sum[i] )点对间的最小距离。
用最近点对的方法求解。
时间复杂度:O(NlgN)
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
给出n(1<=n<=10000)个白点和n个黑点的坐标(不超过10000的整数),要求用n条不相交的线段把它们连接起来,其中每条线段恰好连接一个白点和一个黑点,每个点恰好连接到一条线段。如图所示。
输入保证没有两个坐标相同的点,且任意三点不共线。
所有白点和黑点均按照输入顺序编号为1~n
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
本题可以使用最佳完美匹配解决。这里介绍一种分治的方法。
首先,找出所有的点中纵坐标最小的点(如果纵坐标相同,就取横坐标小的点)记作X。
那么,对于所有除了它之外的点I,向量 XI 的极角就在[0,π)的范围内。
将这些点按照极角从小到大排个序。
假设点X为黑点,一定可以找到一个白点Y,连接X和Y把原来的点分成两部分,这两部分 的黑点和白点数相同,这样就分解出两个问题性质一样的子问题,递归下去即可。
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
把黑点看做1,白点看做-1
则剩下的2n-1个点按照极角排序后就是n-1个1和n个-1组成的序列a[]
可以证明:该序列中一定存在位置i,使得a[i]=-1且序列前缀和s[i]=-1。
证明:在坐标系中画出p1到p2n-1这2n-1个点,点pi横坐标表示位置i,纵坐标表示前缀和s[pi], 相邻点纵坐标相差1或-1,用线段连接相邻点,线段有“/”与“\”两种,“/”表示序列当前位置是1,所以纵坐标增加1,“\”表示序列当前位置是-1,所以纵坐标减少1。因此一定存在某个点px与px+1的连线如图,假如不存在,则所有的点pi就都在x轴上或x轴以上,不可能到达点p2n-1。得证。位置x+1的点px+1就是要寻找的白点,因为a[x+1]=-1,且s[x+1]=-1。
连接X与px+1 ,因为s[x]=0,点集{p1,p2,…,px }和{px+2,px+3,…,p2n-1}都满足黑色点数等于白色点数,可以接下去递归处理。
1
1
-1
2n-1
p1
P2n-1
Px
Px+1
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
另一个分治方法。
直接把点集分成两个不相交子集,两个子集都满足黑色点数等于白色点数
一样,找出所有的点中纵坐标最小的点(如果纵坐标相同,就取横坐标小的点)记作X。 那么,对于所有除了它之外的点I,向量 XI 的极角就在[0,π)的范围内。将这些点按照极角从小到大排个序。
假设X是黑点,排序后如果第1个点是白点,则直接连接,再递归处理剩下的2N-2个点;如果第1个点是黑点,一样把黑点看做1,白点看做-1,前缀和s[2n-1]=-1,s[1],相邻前缀和相差1或-1,从 1(s[1])变成最后的-1(s[2n-1]),则一定存在位置i(1上面两个分治法的时间复杂度都是O(n^2*lgn)。
一维分治3 :UVA 1608 Non-boring sequences
如果一个序列的任意连续子序列至少有一个只出现一次的元素,则称这个序列是不无聊(Non-boring)的。
给一个长度为N的序列A,现要判断它是否是不无聊的。
1<=N ≤ 200000,0<=元素<=10^9
一维分治3 :UVA 1608 Non-boring sequences
采用分治的方法。
如果原数组不存在只出现一次的数,则序列是“无聊”的。
否则假设原数组中仅出现一次的数的位置为p,则我们容易知道包含p的所有区间均是“不无聊”的。我们只需要判断[1,p-1]和[p+1,n]其相应的子区间即可。
在判断某一个区间内某一个数是否出现一次的时候,我们只需要判断和他相同且距离其最近的左边和右边的数是否在此区间内即可,我们可以在O(n)内预处理出L[i]和R[i]。
这样的时间复杂度为O(n^2)。
优化:在区间内寻找该元素的时候从两端向中间寻找,这样的时间复杂度极限为T(n)=2*T(n/2)+O(n),即O(nlgn)。
一维分治3 :UVA 1608 Non-boring sequences
证明如下:
算法时间主要消耗在枚举区间内出现一次的位置p上,从两边枚举,每个区间枚举次数为分割成的较小那块长度的两倍。
T(n)=max{T(k)+T(n-k)+2*min(k,n-k)}
把上图中红色块的长度累加起来就是总枚举次数。
观察每个红色块,其大小一定小于等于其父亲块大小的1/2。
上图递归树中的块,只要长度>1就要继续递归下去,递归树中叶子节点都是长度为1的块,考虑每个位置i对总枚举次数产生的影响,即有多少个红色块包含位置i,从下往上考虑,由于Size(父亲块)>=2*Size(儿子块),所以包含位置i的红色块的数量为O(lgn),所以总时间复杂度为 O(nlgn)。
一维分治4 :CF549F Yura and Developers
给出一个长度为n的序列a和一个整数k。询问有多少个长度大于1的区间满足:在去掉最大值后剩下的数之和能被K整除。
1 ≤ n ≤ 300 000, 1 ≤ k ≤ 1 000 000, 1 ≤ ai ≤ 10^9
一维分治4 :CF549F Yura and Developers
记当前分治区间[L,R]的最大值是am。显然,这个区间的答案就是区间[L,m-1]和区间[m+1,R]以及跨过m的答案之和。
设前缀和数组S[i],那么一个合法的区间[i,j]满足:
所以只要维护左边的Si-1+am就可以了。
一维分治4 :CF549F Yura and Developers
递归树示意如下:
每一层时间复杂度为O(n),深度最坏情况下是O(n),所以时间复杂度最坏情况下为 O(n^2)。
一维分治4 :CF549F Yura and Developers
可以换个思路。刚才是从区间入手,现在从最大值入手。
枚举每个最大值,然后确定出以它为最大值的区间,能向左和向右扩展到哪里,这个可以打两个单调队列解决。剩下就是统计答案了。
首先设s[i]为前缀和,假设最大值为a[m],区间能向左(右)扩展到l[m],r[m]。如果一个以a[m]为最大值的区间[i,j](l[m]≤i≤m,m≤j≤r[m])能够满足条件,当且仅当满足:(s[j]-s[i-1]-a[m])%k=0
统计答案:枚举每个a[m],再枚举以a[m]为最大值的区间的左(或右)边界i,然后就是插入一个形如(l,r,x)的询问,询问有多少个s[j](j∈[l,r]且s[j]=x)。假设有q个询问,解决的时间复杂度为O(q*cost+n)。cost表示每次询问的代价。
一维分治4 :CF549F Yura and Developers
对于询问个数q
如果对于一个m,以a[m]为最大值可以扩展到l[m],r[m],那么相当于把区间[l[m],r[m]]切成两部分,然后如果左半部分比右半部分小,就枚举左边界,否则枚举右边界,那么q是nlogn的。
配合下图,与例1.7 UVA 1608 Non-boring sequences是一样的原理。
一维分治4 :CF549F Yura and Developers
对于询问代价cost
询问有多少个s[j](j∈[l,r]且s[j]=x),直接枚举太慢不可取。
可以把原数组a[i]%k后的值进行排序,并记录每个数的左右界。这样每个询问就可以用二分在O(lgn)内完成。
总时间复杂度为O(n*lgn*lgn) 。用可持久化线段树同样可以做到。
更好的方法:
对于询问(l,r,x)来说,询问的答案为f[r][x]-f[l-1][x],f[r][x]表示s[1],s[2]到s[r]中等于x的个数,维护f很低效。
可以这样做:处理所有询问,每个询问(l,r,x)插入2条记录,一条插入记录(x,-1)到结点l-1的询问链表中,再插入(x,1)到结点r的询问链表中。
记录 cnt[x]表示前缀和为x的出现次数,从小到大枚举位置i,更新cnt[s[i]]++,扫描结点i的询问链表,对于其中的每一个记录(value,sign)更新答案ans+=cnt[value]*sign
均摊下来cost为O(e)。总时间复杂度为O(nlgn)。
一维分治4 :CF549F Yura and Developers
举例:N=4,序列为{4,3,2,5},K=3
枚举a[1],以a[1]为最大值的区间为[1,3],左部分小,枚举左边界L=1,右边界的区间是[2,3],增加一个询问(2,3,1),向结点1插入记录(1,-1),向结点3插入记录(1,1)
枚举a[2],以a[2]为最大值的区间为[2,3],左部分小,枚举左边界L=2,右边界的区间只能取[3,3],增加一个询问(3,3,1),向结点2插入记录(1,-1),向结点3插入记录(1,1)
枚举a[3],以a[3]为最大值的区间为[3,3],不需要考虑
枚举a[4],以a[4]为最大值的区间为[1,4],右部分小,枚举右边界R=4,左边界区间为[1,3],增加询问(0,2,0),向结点-1插入记录(0,-1),向结点2插入记录(0,1)
i -1 0 1 2 3 4
A[i] 0 0 4 3 2 5
L[i] 0 0 1 2 3 1
R[i] 0 0 3 3 3 4
A[i]%K 0 0 1 0 2 2
S[i]%K 0 0 1 1 0 2
-1
0
1
2
3
4
(1,-1)
(1,1)
(1,1)
(1,-1)
(0,-1)
(0,1)
一维分治4 :CF549F Yura and Developers
举例:N=4,序列为{4,3,2,5},K=3
一开始cnt[0]=cnt[1]=cnt[2]=0,ans=0
i=-1,cnt[]={1,0,0},枚举结点-1的询问链表,更新ans=-1
i=0,cnt[]={2,0,0},结点0后没有询问链表,ans保持不变
i=1,cnt[]={2,1,0},枚举结点1的询问链表,ans=ans+cnt[1]*-1=-2
i=2,cnt[]={2,2,0},枚举结点2的询问链表,ans=ans+cnt[1]*-1+cnt[0]*1=-2
i=3,cnt[]={3,2,0},枚举结点3的询问链表,ans=ans+cnt[1]*1+cnt[1]*1=2
i=4,cnt[]={3,2,1},结点4后没有询问链表,ans保持不变
Ans=2,对应的两个区间是[4,3]和[4,3,2,5]。
i -1 0 1 2 3 4
A[i] 0 0 4 3 2 5
L[i] 0 0 1 2 3 1
R[i] 0 0 3 3 3 4
A[i]%K 0 0 1 0 2 2
S[i]%K 0 0 1 1 0 2
-1
0
1
2
3
4
(1,-1)
(1,1)
(1,1)
(1,-1)
(0,-1)
(0,1)
一维分治5:计蒜之道 百度地图的实时路况
给一个有N(4<=N<=300)个点的无向图。定义d(x,y,z)为从x号点出发,严格不经过y号点,最终到达z号点的最短路径长度。如果这样的路径不存在,d(x,y,z)的值为-1.
求
一维分治5:计蒜之道 百度地图的实时路况
这题类似Floyd,但是是求不经过某个点的时候,所有点之间两两的最短路。
可以枚举不经过的点然后Floyd,时间复杂度为O(n^4)。
但是考虑到每个不经过的点的时候,其实有很多的两点之间的距离并不会改变,有重复计算。
分治:对于一个分治区间[l,r],我们会处理出一个最短路矩阵,表示不以[l,r]区间的点作为中转点的最短路。那么从[l,r]递归到[l,mid]只需要枚举[mid+1,r]的点作为k(中转点)在原矩阵的基础上跑Floyd,就能计算出[l,mid]对应的矩阵,[mid+1,r]也是同理在[l,r]最短路矩阵的基础上把[l,mid]中的点添加到允许经过的点中就可以计算出[mid+1,r]对应的矩阵。
最后分治区间长度为1的时候,就是不以对应点为中转点的最短路矩阵了。时间复杂度是O(n^3*lg n)。
二维分治1:CF480E Parking Lot
给出一个n×m(n,m<=2000)的网格图,有的位置上有障碍物。给出k(k<=2000)个操作,每次将一个格子变为障碍物,再询问没有障碍物的最大子正方形。
Time Limit: 3s
二维分治1:CF480E Parking Lot
定义f[i][j]表示以第i行第j列为右下角的最大子正方形的边长。
对于每次操作,利用动态规划f[i][j]=min{f[i-1][j-1],f[i-1][j],f[i][j-1]}+1
时间复杂度为O(nmk),超时。
可以用分治
定义f[L][R]表示原网格图第L行到第R行k次操作后的最大子正方形大小。
将矩阵尽可能分成上下相等的两部分。设中间一行为mid。
那么f[L][R]就是以下3部分的最大值。
①f[L,mid]
②f [mid+1,R]
③穿过mid这一行的最大子正方形
前两个可以分治递归求解。
二维分治1:CF480E Parking Lot
对于跨过中间mid一行的正方形:
每个格点维护up[i][j]和down[i][j],up[i][j]表示从位置(i,j)开始向上有多少个连续的无障碍的位置,down[i][j]表示从位置(i,j)开始向下有多少个连续的无障碍的位置,初始的up和down可以用递推在O(nm)内完成。
按顺序处理每个操作,对于每个在当前分治范围内的操作(x,y),只会影响第y列的up和down的值,在O(n)内更新这些值。
跨过中线的最大正方形,一定包含第mid行,考虑该正方形左边界为列号i,右边界为列号j。
先枚举左边界i,再枚举右边界j,则包含第x行第i列到第j列的矩形的宽度w=j-i+1,高度h=min_up+min_down-1,该情况下的最大子正方形的边长为min(w,h),其中min_up=min{up[mid][i],up[mid][i+1],…,up[mid][j]},min_down{down[mid][i],down[mid][i+1],…,down[mid][j]}
第mid行
第i列
第j列
min_up
min_down
二维分治1:CF480E Parking Lot
min_up和min_down的计算可以通过维护两个单调递增的队列来实现,因为是计算区间最小值,当后面出现更小的值时可以删除前面比该值大的元素, min_up和min_down的值分别在队列的第1个位置。
容易知道,宽度w在递增,高度h非递增,所以当h左边界i向右枚举过程中,最大的合法右边界j也是非递减的。
每次递归返回的是k次操作后的子正方形大小,可能只有其中一部分操作在当前递归区间内,对于不在区间的操作直接赋为最靠近的前面一个操作后的答案,比如第x操作后的答案为value,下一次操作是y,则第x+1,x+2,…,y-1操作后的答案直接赋为value即可。
所以对于每次操作,计算跨过中间mid一行的正方形的大小可以在O(m)内完成,分治过程中对于每个操作最多有lgn的分治区间包含它。所以总时间复杂度为O((m+n)*k*lgn)。
min_up
min_down
二维分治1:CF480E Parking Lot
更好的方法:
离线处理,先把最后的答案用动态规划在O(n*m)完成。
从后往前做,每次相当于把一个障碍物变成非障碍物,答案肯定非递减。
对于操作(x,y),在O(n)内更新第y列的up和down的值。
如果答案增大,一定跟第x行有关系,所以我们就处理包含第x行的答案,处理方法跟前面计算跨过中线的答案一样,处理每个操作的时间复杂度为O(m)。
总时间复杂度是O(n*m+m*k)。
二维分治2:CF364E Empty Rectangle
给出一个n*m(1<=n,m ≤ 2500)的01网格,求有多少矩形中恰好包含k(0<=k<=6)个1。
Time Limit: 12s
二维分治2:CF364E Empty Rectangle
方法一:
初始化s[i][j]表示以(1,1)为左上角(i,j)为右下角的矩形中的元素之和
递推O(nm)内解决:s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j]
枚举左上角(x1,y1)和右下角(x2,y2)判断s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]是否等于k。
时间复杂度为(n^2*m^2)。超时。
方法二:
枚举左边界L,右边界R,下边界B,上边界是可以用二分计算出来。
时间复杂度为O(n*m^2*lgn)。
二维分治2:CF364E Empty Rectangle
方法三:分治法
像例1.10那样定义f[L][R]表示原矩阵第L行到第R行1的个数等于k的子矩阵的数量。
将矩阵尽可能均分成两部分。设中间一行为mid。
那么f[L][R]就是以下3部分的最大值。
①f[L,mid]
②f [mid+1,R]
③穿过mid这一行格点满足要求的子矩阵的数量,注意该矩阵必须包含第mid行和第mid+1行。
前两个可以分治递归求解。
二维分治2:CF364E Empty Rectangle
计算穿过第mid这一行的数量,可以枚举左边界i,再枚举右边界j
定义up[x]表示以i为左边界、j为右边界、mid为下边界的1的个数不超过x的最大矩形的上边界,则1的个数等于x的红色矩形有up[x-1] -up[x]个。同理定义down[x]表示以i为左边界、j为右边界、mid+1为上边界的1的个数不超过x的最大矩形的下边界,则1的个数等于x的绿色矩形有down[x]-down[x-1]个。
随着j的右移,up[x]是单调增的,down[x]是单调减的
统计答案:枚举x,ans+=(up[x-1]-up[x])*(down[k-x]-down[k-x-1]),具体实现要注意其他细节。
合并这一步操作时间复杂度为O(m*m*k)
T(n)=2*T(n/2)+m*m*k
T(n)=O(n*m*m*k)(注意与上题的区别!!)
mid
i
j
二维分治2:CF364E Empty Rectangle
T(n)=2*T(n/2)+m*m*k
=2*(2*T(n/4)+m*m*k)+m*m*k
=4*T(n/4)+2*m*m*k+m*m*k
=…
≈2*n*m*m*k=O(n*m*m*k)
n
n/2
n/2
n/4
n/4
n/4
n/4
1
1
1
1
1
1
1
1
m*m*k
2*m*m*k
4*m*m*k
n*m*m*k
lgn
二维分治2:CF364E Empty Rectangle
采用二维分治,横向划分和纵向划分相结合
递归树示意图如下:
总时间复杂度为O(k*(m*m*logn+n*n*logm))
也可以每次分成4块分治下去,时间复杂度一样。
m*m*k
m*m*k
n*n*k/2
n*n*k/2
点分治1:Poj1741 树中点对统计
给定一棵N(1<=N<=10000)个结点的带权树,定义为dis(u,v)为u,v两点间的最短路径长度,路径的长度定义为路径上所有边的权和。 再给定一个K(1<=K<=10^9),如果对于不同的两个结点a,b,满 足dis(a,b)<=K,则称(a,b)为合法点对。求合法点对个数。
点分治1:Poj1741 树中点对统计
方法一:
以每一个点为起点出发做DFS,统计出任意点对的最短路径长度,时间复杂度高达O(N^2)
方法二:
一条路径要么过根结点,要么在根结点的某一个子树中,可以用分治算法。
路径在子树中的情况递归处理即可,下面分析经过根结点的情况。
点分治1:Poj1741 树中点对统计
定义Depth(i)表示点i到根结点的路径长度,Belong(i)=X ( X 为根结点的某个儿子,且结点i在以X为根的子树内)。那么我们要统计的就是:
满足Depth(i)+Depth(j)<=K且Belong(i)≠Belong(j)的(i,j)个数
=满足Depth(i)+Depth(j)<=K的(i, j)个数–
满足Depth(i)+Depth(j)<=K且Belong(i)=Belong(j)的(i, j)个数
这两个部分都是要求满足Ai+Aj<=k的(i,j)的对数。可以将A排序后利用单调性我们很容易得出一个O(N)的算法,所以我们可以用O(NlogN)的时间来解决这个问题。
综上,此题使用分治算法的时间复杂度为 O(N*logN*递归深度) 。
点分治1:Poj1741 树中点对统计
递归深度取决于选择的根结点。
最佳选择是选一个点作为根结点,使得其结点最多的子树的结点数最小,也被称为“树的重心”,可以用树形DP在O(N)内求出。
定理:树的重心分出的子树的结点个数均不大于N/2。
证明:假设U是树的重心,它与V1,V2,…,Vk相邻,记Size(X)表示 以X为根的子树的结点个数。记V为V1,V2,…,Vk中Size值最大的点。 采取反证法,假设Size(V)>N/2,那么我们考虑如果选取V作为根结点的情况,记Size’(X)表示此时以X为根的子树的结点个数。 如下图,对于A部分,显然Size’(Ti)点分治1:Poj1741 树中点对统计
每次递归选择子树的重心做为树根,max_i表示第i层的子树结点最多的结点数,有max_1<=N,max_2<=N/2,max_i<=N/(2^(i-1)),递归深度为O(logN)。
总时间复杂度为O(N*logN*logN)。
max_1<=N
max_2<=N/2
max_3<=N/4
O(logN)
点分治1:Poj1741 树中点对统计—代码
void solve(int u) //计算以u为根的子树中dis(a,b)<=K的点对数。
{
int G = calcG(u);//寻找树的重心G
vis[G] = true;
ans += calc(G, 0);//统计满足Depth(i)+Depth(j)<=K的(i, j)个数
for (int e = adj[G]; e; e = nxt[e])
if (!vis[go[e]]) ans -= calc(go[e], len[e]);
//统计满足Depth(i)+Depth(j)<=K且Belong(i)=Belong(j)的(i, j)个数
for (int e = adj[G]; e; e = nxt[e])
if (!vis[go[e]]) solve(go[e]);//递归处理G的子树
}
点分治1:Poj1741 树中点对统计—代码
long long calc(int sv, int L){ //计算以sv为根的子树中到根sv的距离<=K-L的结点数。
static int qn, que[N], d[N];
int u, v, e, d_n = 0;
que[qn = 1] = sv, dis[sv] = L, fa[sv] = 0;
for (int ql = 1; ql <= qn; ++ql) {
d[d_n++] = dis[u = que[ql]];
for (e = adj[u]; e; e = nxt[e]) {
if (vis[v = go[e]] || v == fa[u]) continue;fa[v] = u, dis[v] = dis[u] + len[e], que[++qn] = v;
}
}//宽搜
long long cnt = 0;
std::sort(d, d + d_n);
int l = 0, r = d_n - 1;
while (l < r) { if (d[l] + d[r] <= K) cnt += r - l++; else –r; }//使用双指针利用单调性统计答案。
return cnt;
}
点分治1:Poj1741 树中点对统计
也可以把前面已经完成的子树中的距离加入到平衡树,下一个子树中每计算出一个距离就到平衡树中统计答案,一个子树中全部处理完再加入到平衡树中。
常数更小的写法:
增加B[],B[x]记录x在root的哪个子结点的子树中,B[root]=root
计算经过根结点路径点对:“满足Depth(i)+Depth(j)<=K的(i, j)个数”–
“满足Depth(i)+Depth(j)<=K且Belong(i)=Belong(j)的(i, j)个数”时,可以不用多次调用clac()。直接把树中的点都取出来放进数组中,按照D[x]递增排序。
还是用两个指针 i, j ,i从左开始枚举,表示路径到root距离较小的端点,j从后向前开始扫描数组,可以计算出满足D[x]+D[y]<=k的合法点对(x,y)的个数,其中x、y分别是i、j指向的节点编号。
计算方法如下:
设F[i]表示在左、右指针中间满足B[x]=i的点x的个数,先初始化F[],枚举过程中i向右加1前先执行F[B[node[i]]]--,j减1前线执行F[B[node[j]]]-- 。
设当前左指针指向点x,则 j-i-F[B[x]] 就是要求的答案。
排序是O(NlogN)的,扫描是O(N)的。总时间复杂度还是O(N*logN*logN),但常数减小。
点分治2: CF293E Close Vertices
给一棵N个顶点的树,求有多少条路径的边数不超过L,且边权和小于等于W。
1 ≤ N ≤ 105 1 ≤ L ≤ N 0 ≤ W ≤ 109
Time Limit: 3s
点分治2: CF293E Close Vertices
用树分治,比上题多边数限制。做法与上一题类似:
把路径分成两类:
①在根的子结点为根的子树中,递归处理即可;
②路径经过根结点
②的处理方法跟上题代码中一样,等于calc(root,0)-∑calc(son_i,edge(root,son_i))
计算calc()时,一样按照到根结点root的距离从小到大排序,从右往左一个端点i,另外一个端点j从小到大递增,j每次向右移,就把新加入的结点node[j]对应的num[node[j]](到根结点的边数)添加到树状数组中,再统计数状数组中<=W-num[node[i]]的个数即可。
总时间复杂度是O(N*logN*logN)。
点分治3:WC2010重建计划
给出一棵N个节点带权树。
求边数在[L,R]之间的所有路径中,最大的权值平均值。
N ≤ 100000
点分治3:WC2010重建计划
二分答案mid,将图中所有边减mid,问题转换为判断是否存在边数为x的路径,路径边权和>=0,L<=x<=R。
对于递归执行的每棵树,先找出重心,从重心剖开树以后,得到若干棵子树
顺序处理每棵子树,对于一棵子树,Bfs得其所有路径边数及边权和(起点从重心出发,终点在该子树内),由于是Bfs,所以路径长度是从小到大
并维护mx[i]表示起点从重心出发,终点在子树内,长度为i的路径边权和最值,当前正在处理的子树中的信息先不添加到mx[]中,处理完再把这些信息更新到mx[]中
Bfs处理子树中路径i,路径i的长度为x,则需要维护mx中长度在区间[L-x,R-x]内的最大值,该区间是向左平移的,可以维护单调递减队列。
时间复杂度为O(N*logN*logN)。
分治算法
2023年高中信息技术教学课件
主要内容
1.分治思想
2.经典问题
3.基于一维的分治
4.基于二维的分治
5.点分治
分治思想
分治(Divide-And-Conquer)就是“分而治之”的意思,其实质就是将原问题分成n个规模较小而结构与原问题相似的子问题;然后递归地解这些子问题,最后合并其结果就得到原问题的解。
其三个步骤如下:
①划分问题(Divide):将原问题分成一系列子问题。
②递归解决(Conquer):递归地解各子问题。若子问题足够小,则可直接求解。
③合并问题(Combine):将子问题的结果合并成原问题的解。
如快速排序、归并排序等都是采用分治思想。
分治算法设计过程图
问题S
问题S
问题S
S的解
问题S1
……
问题S2
问题Si
问题Sn
……
S1的解
……
S2的解
Si的解
Sn的解
……
问题的分解
子集解的合并
递归求解子问题
经典问题1—棋盘覆盖
有一个2k*2k的方格棋盘,恰有一个方格是黑色的,其他为白色。你的任务是用包含3个方格的L型牌覆盖所有白色方格。黑色方格不能被覆盖,且任意一个白色方格不能同时被两个或更多牌覆盖。如下图所示为L型牌的4种旋转方式。
经典问题1—棋盘覆盖
题目是要求用L型牌覆盖一个2k*2k的方格棋盘,棋盘有且只有一个黑色方格,且此方格不能被覆盖。
用分治来解决,把原棋盘平均分为4块,通过用1个L型牌覆盖棋盘正中间2*2的区域中的三个格子,把原棋盘分成4块2k-1*2k-1的方格棋盘,且每块中只含有一个黑色方格(不能覆盖的格子)。
此时把原问题分解成4个结构与原问题一样的子问题,棋盘的大小(边长)每次减半,最终会出现边长为1的情况,直接求解即可。
经典问题1—棋盘覆盖
定义cover(x,y,len,x0,y0)表示求解左上角格子在(x,y)边长为len,其中(x0,y0)不能覆盖的棋盘覆盖方案。
根据黑色格子的位置分为以下四种情况:
情况1:黑点位于左上部分
情况2:黑点位于左下部分
递归求解
划分问题
左上:cover(x,y,len/2,x0,y0)
左下:cover(x+len/2,y,len/2,x+len/2,y+len/2-1)
右上:cover(x,y+len/2,len/2,x+len/2-1,y+len/2)
右下:cover(x+len/2,y+len/2,len/2,x+len/2,y+len/2)
递归求解
划分问题
左上:cover(x,y,len/2,x+len/2-1,y+len/2-1)
左下:cover(x+len/2,y,len/2,x0,y0)
右上:cover(x,y+len/2,len/2,x+len/2-1,y+len/2)
右下:cover(x+len/2,y+len/2,len/2,x+len/2,y+len/2)
经典问题1—棋盘覆盖
情况3:黑点位于右上部分
情况4:黑点位于右下部分
每个格子只会被处理一次,时间复杂度为O(n^2),n为棋盘边长。
递归求解
划分问题
左上:cover(x,y,len/2, x+len/2-1,y+len/2-1)
左下:cover(x+len/2,y,len/2,x+len/2,y+len/2-1)
右上:cover(x,y+len/2,len/2,x0,y0)
右下:cover(x+len/2,y+len/2,len/2,x+len/2,y+len/2)
递归求解
划分问题
左上:cover(x,y,len/2,x+len/2-1,y+len/2-1)
左下:cover(x+len/2,y,len/2,x+len/2,y+len/2-1)
右上:cover(x,y+len/2,len/2,x+len/2-1,y+len/2)
右下:cover(x+len/2,y+len/2,len/2,x0,y0)
经典问题1—棋盘覆盖—代码
void cover(int x,int y,int len,int x0,int y0)
{
int t,len1;
if (len==1)return;
t=++tot;
len1=len/2;
if (x0
if (x0>=x+len1&&y0
if (x0
else{board[x+len1-1][y+len1]=t;cover(x,y+len1,len,x+len1-1,y+len1);}
if (x0>=x+len1&&y0>=y+len1)cover(x+len1,y+len1,len1,x0,y0);
else{board[x+len1][y+len1]=t;cover(x+len1,y+len1,len1,x+len1,y+len1);}
}
经典问题2—归并排序
给定一个长度为N的序列,对其进行排序。
归并排序思想:
1.划分问题:把长度为N的序列尽可能均分成左右两部分;
2.递归求解:对左右两部分分别进行归并排序;
3.合并问题:把左右两段排好序的序列合并出最终的有序序列。
经典问题2—归并排序
举例:N=8,8个数分别为6,1,5,3,2,4,8,7。过程如下:
6
5
1
3
4
2
7
8
6
5
1
3
4
2
7
8
6
1
5
3
4
2
7
8
6
1
5
3
2
4
8
7
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
划分
合并
合并
合并
合并
合并
合并
合并
1
3
2
4
6
5
8
7
1
5
3
6
4
2
8
7
1
6
3
5
4
2
8
7
经典问题2—归并排序
第3步如何把两段排好序的序列合并成一个有序序列?
考虑第一段中两个数A[i],A[j],如果i
1
3
5
6
2
4
7
8
1
2
3
4
5
6
7
8
经典问题2—归并排序—代码
void merge(l,m,r)// 合并操作
{
// i 代表左半序列目前最小的位置
// j 代表右半序列目前最小的位置
// a:原数组b 数组:暂存数组(合并过程不能覆盖原数组)
int i = l, j = m+1, k = l;
for(; i<=m && j<=r; )
if(a[i] <= a[j]) b[k++] = a[i++]; // 加入左边最小的
else b[k++] = a[j++]; // 加入右边最小的
// 加入剩余的数
for(; i<=m; b[k++] = a[i++]); // 加入剩余左半的数
for(; j<=r; b[k++] = a[j++]); // 加入剩余右半的数
for(i=l; i<=r; i++) a[i] = b[i]; // 从暂存数组中赋值
}
经典问题2—归并排序—代码
void merge_sort(int l, int r) // 排序位置从l 到r 的序列
{
if(l==r) return; // 长度为1 则不需要排序
int m = (l+r) / 2; // 分成两段
merge_sort(l, m); // 排序左半段
merge_sort(m+1, r); // 排序右半段
merge(l,m,r);//把两段排好序的序列合并成一个有序序列
}
经典问题2—归并排序—时间复杂度分析一
F(n)表示对n个数进行归并排序的时间复杂度
根据归并排序思想有:
F(n)=2*F(n/2)+n
设n’=2^k,k=lgn’,则有:
F(n’)=2*F(n’/2)+n’=2*(2*F(n’/4)+n’/2)+n’=4*F(n’/4)+2*n’
=4*(2*F(n’/8)+n’/4)+2*n’=8*F(n’/8)+3*n’
=……=2^k*F(1)+k*n’=2^k+k*2^k=n’+n’*lgn’
设n’<=n<2*n’,则有F(n’)<=F(n)
n’+n’lgn’<=F(n)<=2*n’+2*n’*lg2+2*n’*lgn’
所以F(n)=O(nlgn)。
经典问题2—归并排序—时间复杂度分析二
画出归并排序的递归树。
时间主要花费在合并上,每一层合并代价综合为n,树的深度为lgn,所以时间复杂度为O(nlgn)。
n
n/2
n/2
n/4
n/4
n/4
n/4
1
1
1
1
1
1
1
1
n
n
n
n
lgn
经典问题3—逆序对统计
给定一个长度为N 的序列,定义它的逆序对数为;
二元组(i,j),满足i
例如:对于A=[3 2 5 1 4],逆序对数为5:3>2, 3>1, 2>1,5>1, 5>4。
经典问题3—逆序对统计
下面介绍一种使用归并排序计算逆序对的方法(利用分治算法的思想) 。
长度为N 的序列的逆序对数ans 可以分为3部分:
① 左半段的逆序对数L_ans
②右半段的逆序对数R_ans
③(i,j)分立两侧的逆序对数C_ans
* 结论:ans = L_ans + R_ans + C_ans
例如:对于A=[3 2 5 1 4],分成两段A1 = [3 2 5], A2 = [1 4]
L_ans= 1(3>2), R_ans = 0, C_ans = 4(3>1, 2>1, 5>1, 5>4)
ai
aj
ai
aj
ai
aj
经典问题3—逆序对统计
ans = L_ans + R_ans + C_ans
其中L_ans,R_ans是与计算ans相同类型的子问题,递归计算即可。主要考虑(i,j)分立两侧的逆序对数C_ans:
结论:对两半段的数分别排序, (i 在左半段,j 在右半段,排在不同位置不影响先后关系) ,C_ans 不变
例如:对于A=[3 2 5 1 4],分成两段A1 = [3 2 5], A2 = [1 4],对A1 和A2 进行排序,A’ = [2 3 5 1 4], C_ans 仍然为4(3>1,2>1, 5>1, 5>4)
经典问题3—逆序对统计
考虑(i,j)分立两侧的逆序对数C_ans:
考虑在合并过程中,统计它们的分立两侧逆序对总数:
左部分区间为[L,m],右部分[m+1,r],在合并过程中,左右指针分别为i,j,当出现A[i]>A[j]时,(i,j)是一个逆序对,且A[L..m]是升序,所以(i+1,j),(i+2,j)…(m,j)也都是逆序对,答案ans可以直接增加m-i+1。
经典问题3—逆序对统计
如N=8,序列为[6,1,5,3,2,4,8,7],分成[6,1,5,3],[2,4,8,7]左右两段, 递归计算出L_ans=4,R_ans=1,两部分排好序分别为[1,3,5,6],[2,4,7,8],C_ans的计算如下:
1
3
5
6
2
4
7
8
1
2
3
4
5
6
7
8
C_ans=
0
+3=3
+2=5
经典问题3—逆序对统计—代码
可以直接套用归并排序的模板,在合并过程顺便统计逆序对数。对于合并程序稍作改变。
void merge(l,m,r)// 合并操作,同时统计逆序对
{
int i = l, j = m+1, k = l;
for(; i<=m && j<=r; )
if(a[i] <= a[j]) b[k++] = a[i++]; // 加入左边最小的
else ans += m-i+1,b[k++] = a[j++];
// 插入右半段的时候,逆序对数增加
for(; i<=m; b[k++] = a[i++]); // 加入剩余左半的数
for(; j<=r; b[k++] = a[j++]); // 加入剩余右半的数
for(i=l; i<=r; i++) a[i] = b[i]; // 从暂存数组中赋值
}
经典问题4—最近点对问题
给定平面上n(n>=2)个点,计算最近点对的距离。距离指欧几里得距离。即点p1(x1,y1)和p2(x2,y2)之间的距离为。可能有点重合,在这种情况下,它们之间的距离为0。这一问题可以应用于交通控制等系统中,在空中或海洋交通控制系统中,需要发现两个距离最近的交通工具,以便检测出可能发生的相撞事故。
经典问题4—最近点对问题
方法一:暴力枚举
共C(n,2)=n*(n-1)/2个点对,时间复杂度为O(n^2)。
经典问题4—最近点对问题
方法二:考虑用分治
ans表示n个点的最近点对距离,先判重,如有点重合ans=0。
否则把n个点尽可能均分为左右两部分,ans的值只有以下3种情况:
1.左边部分的最近点对距离d1
2.右边部分的最近点对距离d2
3.左半部分的点与右半部分点形成的最小距离d3
ans=min(min(d1,d2),d3)
左右两部分的最近点对问题是与原问题结构性质一样的子问题,可以递归求解出d1,d2
第3部分d3的求解是问题的关键。
经典问题4—最近点对问题
分治法的时间复杂度T(n)=2*T(n/2)+D(n),其中D(n)表示计算d3的时间复杂度。
如果d3的计算采用普通枚举法,两两枚举左右两部分的点对,则D(n)=n*n/4
设n=2^k
T(n)=2*T(n/2)+n*n/4
=2*(2*T(n/4)+n*n/16)+n*n/4
=4*T(n/4)+n*n/8+n*n/4
=8*T(n/8)+n*n/16+n*n/8+n*n/4
=…=2^k*T(1)+n^2/4+n^2/8+…+n^2/(2^(k+1))
=(n^2+n)/2=O(n^2)
并没有比暴力枚举快多少。
经典问题4—最近点对问题
如果D(n)=c*n,则T(n)=2*T(n/2)+c*n=O(nlgn)
D(n)=c*n,说明计算d1,d2,d3时不能采用排序。做法如下:
1.前期准备:一开始,把输入的n个点复制到A和B数组中,对A数组按x坐标单调递增的顺序排序,对B数组按y坐标单调递增的顺序排序,并建立映射Index[],Index[i]表示B数组第i个点在A数组的第Index[i]位置,即B[i]与A[Index[i]]是同一个点。接下来进行判重,如有点重合,则返回答案为0。否则进入第二步开始递归
2.算法的每一次递归调用的输入都是点集对应的数组A和B,如果点数n<=3,则直接暴力枚举。如n>3则:
经典问题4—最近点对问题
①划分问题:直接用数组A的中间位置m作为分界点,A数组中m左侧(含m)的点为左半部分的点,m右侧的点为右半部分的点,数组A很容易就被划分为AL和AR ,从左到右扫描B中的点,判断Index[i]与m的大小关系,如Index[i]<=m,则该点属于BL否则属于BR,同时更新BL和BR对应的Index[]。时间复杂度为O(n)
②递归解决:递归求解出左右两部分的最近点对距离d1,d2,取较小值d=min(d1,d2)
经典问题4—最近点对问题
③合并问题:答案ans=min(d,d3),d3表示左半部分的点到右半部分点的最短距离,如果存在点对使得d3
经典问题4—最近点对问题
1)建立数组B’,它是把数组B中所有不在宽度为2d的垂直带形区域内的点去掉后得到的数组,所以B’也是按y坐标顺序排序的。
2)从左到右扫描B’中的每一个点p,尝试找出后面与p距离小于d的点。下面将会看到,仅需考虑紧随p后面的6个点,并记录下B’中所有点对的最小距离d3。
3)如果d3
经典问题4—最近点对问题
正确性
枚举宽度为2d的带形区域中的一点p,考虑其后面的点p’
如果dis(p,p’)
d
d
p
经典问题4—最近点对问题
正确性
观察属于左半部分的d*d的正方形区域,如该区域内的点全部属于左半部分,通过横向纵向两条直线把d*d的正方形区域均分为4个d/2*2/2的小正方形,因为每个小正方形最远的两个点的距离为对角线即sqrt(2)*d/2
经典问题4—最近点对问题
正确性
再仔细分析,如果有8个点,则一定有两对点是重合的,而算法一开始就已经排除了重复。
那是不是就一共只有6个点,只需判断后面的5个点呢?
下面如图所示是7个点的情况,所以最多是7个点,只需判断后面的6个点。
经典问题4—最近点对问题
算法导论中不严谨之处?
算法导论指出:只需考虑p后面的7个点,因为2d*d区域因为重合点最多有8个点。
问题是:如果有重合点可能就不是2个点重合,可能是3个,4个甚至更多。
当然:算法导论的做法不影响结果,因为如果更多的点重合,在递归时就已经算出d=0,后面判断7个点不影响结果,如果没有点重合,只需判断6个点,那么判断7个点也不影响正确性。
即使你不清楚上面的性质,但一开始进行了判重,且在枚举p’时增加了纵坐标相差不超过d的判断,一样可以在O(nlgn),因为你无形之中用了上面的性质。
一维分治1:CF429D Tricky Function
给出一个长度为N的序列a。
定义
求最小的f(i,j)
N ≤ 100000
Time Limit: 2s
一维分治1:CF429D Tricky Function
设Sum[i]表示a[1]+a[2]+…+a[i]
那么g(i,j)=Sum[j]-Sum[i]
问题变成:求形如( i , Sum[i] )点对间的最小距离。
用最近点对的方法求解。
时间复杂度:O(NlgN)
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
给出n(1<=n<=10000)个白点和n个黑点的坐标(不超过10000的整数),要求用n条不相交的线段把它们连接起来,其中每条线段恰好连接一个白点和一个黑点,每个点恰好连接到一条线段。如图所示。
输入保证没有两个坐标相同的点,且任意三点不共线。
所有白点和黑点均按照输入顺序编号为1~n
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
本题可以使用最佳完美匹配解决。这里介绍一种分治的方法。
首先,找出所有的点中纵坐标最小的点(如果纵坐标相同,就取横坐标小的点)记作X。
那么,对于所有除了它之外的点I,向量 XI 的极角就在[0,π)的范围内。
将这些点按照极角从小到大排个序。
假设点X为黑点,一定可以找到一个白点Y,连接X和Y把原来的点分成两部分,这两部分 的黑点和白点数相同,这样就分解出两个问题性质一样的子问题,递归下去即可。
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
把黑点看做1,白点看做-1
则剩下的2n-1个点按照极角排序后就是n-1个1和n个-1组成的序列a[]
可以证明:该序列中一定存在位置i,使得a[i]=-1且序列前缀和s[i]=-1。
证明:在坐标系中画出p1到p2n-1这2n-1个点,点pi横坐标表示位置i,纵坐标表示前缀和s[pi], 相邻点纵坐标相差1或-1,用线段连接相邻点,线段有“/”与“\”两种,“/”表示序列当前位置是1,所以纵坐标增加1,“\”表示序列当前位置是-1,所以纵坐标减少1。因此一定存在某个点px与px+1的连线如图,假如不存在,则所有的点pi就都在x轴上或x轴以上,不可能到达点p2n-1。得证。位置x+1的点px+1就是要寻找的白点,因为a[x+1]=-1,且s[x+1]=-1。
连接X与px+1 ,因为s[x]=0,点集{p1,p2,…,px }和{px+2,px+3,…,p2n-1}都满足黑色点数等于白色点数,可以接下去递归处理。
1
1
-1
2n-1
p1
P2n-1
Px
Px+1
一维分治2:蚂蚁(Ants,NEERC2008,LA4043)
另一个分治方法。
直接把点集分成两个不相交子集,两个子集都满足黑色点数等于白色点数
一样,找出所有的点中纵坐标最小的点(如果纵坐标相同,就取横坐标小的点)记作X。 那么,对于所有除了它之外的点I,向量 XI 的极角就在[0,π)的范围内。将这些点按照极角从小到大排个序。
假设X是黑点,排序后如果第1个点是白点,则直接连接,再递归处理剩下的2N-2个点;如果第1个点是黑点,一样把黑点看做1,白点看做-1,前缀和s[2n-1]=-1,s[1],相邻前缀和相差1或-1,从 1(s[1])变成最后的-1(s[2n-1]),则一定存在位置i(1
一维分治3 :UVA 1608 Non-boring sequences
如果一个序列的任意连续子序列至少有一个只出现一次的元素,则称这个序列是不无聊(Non-boring)的。
给一个长度为N的序列A,现要判断它是否是不无聊的。
1<=N ≤ 200000,0<=元素<=10^9
一维分治3 :UVA 1608 Non-boring sequences
采用分治的方法。
如果原数组不存在只出现一次的数,则序列是“无聊”的。
否则假设原数组中仅出现一次的数的位置为p,则我们容易知道包含p的所有区间均是“不无聊”的。我们只需要判断[1,p-1]和[p+1,n]其相应的子区间即可。
在判断某一个区间内某一个数是否出现一次的时候,我们只需要判断和他相同且距离其最近的左边和右边的数是否在此区间内即可,我们可以在O(n)内预处理出L[i]和R[i]。
这样的时间复杂度为O(n^2)。
优化:在区间内寻找该元素的时候从两端向中间寻找,这样的时间复杂度极限为T(n)=2*T(n/2)+O(n),即O(nlgn)。
一维分治3 :UVA 1608 Non-boring sequences
证明如下:
算法时间主要消耗在枚举区间内出现一次的位置p上,从两边枚举,每个区间枚举次数为分割成的较小那块长度的两倍。
T(n)=max{T(k)+T(n-k)+2*min(k,n-k)}
把上图中红色块的长度累加起来就是总枚举次数。
观察每个红色块,其大小一定小于等于其父亲块大小的1/2。
上图递归树中的块,只要长度>1就要继续递归下去,递归树中叶子节点都是长度为1的块,考虑每个位置i对总枚举次数产生的影响,即有多少个红色块包含位置i,从下往上考虑,由于Size(父亲块)>=2*Size(儿子块),所以包含位置i的红色块的数量为O(lgn),所以总时间复杂度为 O(nlgn)。
一维分治4 :CF549F Yura and Developers
给出一个长度为n的序列a和一个整数k。询问有多少个长度大于1的区间满足:在去掉最大值后剩下的数之和能被K整除。
1 ≤ n ≤ 300 000, 1 ≤ k ≤ 1 000 000, 1 ≤ ai ≤ 10^9
一维分治4 :CF549F Yura and Developers
记当前分治区间[L,R]的最大值是am。显然,这个区间的答案就是区间[L,m-1]和区间[m+1,R]以及跨过m的答案之和。
设前缀和数组S[i],那么一个合法的区间[i,j]满足:
所以只要维护左边的Si-1+am就可以了。
一维分治4 :CF549F Yura and Developers
递归树示意如下:
每一层时间复杂度为O(n),深度最坏情况下是O(n),所以时间复杂度最坏情况下为 O(n^2)。
一维分治4 :CF549F Yura and Developers
可以换个思路。刚才是从区间入手,现在从最大值入手。
枚举每个最大值,然后确定出以它为最大值的区间,能向左和向右扩展到哪里,这个可以打两个单调队列解决。剩下就是统计答案了。
首先设s[i]为前缀和,假设最大值为a[m],区间能向左(右)扩展到l[m],r[m]。如果一个以a[m]为最大值的区间[i,j](l[m]≤i≤m,m≤j≤r[m])能够满足条件,当且仅当满足:(s[j]-s[i-1]-a[m])%k=0
统计答案:枚举每个a[m],再枚举以a[m]为最大值的区间的左(或右)边界i,然后就是插入一个形如(l,r,x)的询问,询问有多少个s[j](j∈[l,r]且s[j]=x)。假设有q个询问,解决的时间复杂度为O(q*cost+n)。cost表示每次询问的代价。
一维分治4 :CF549F Yura and Developers
对于询问个数q
如果对于一个m,以a[m]为最大值可以扩展到l[m],r[m],那么相当于把区间[l[m],r[m]]切成两部分,然后如果左半部分比右半部分小,就枚举左边界,否则枚举右边界,那么q是nlogn的。
配合下图,与例1.7 UVA 1608 Non-boring sequences是一样的原理。
一维分治4 :CF549F Yura and Developers
对于询问代价cost
询问有多少个s[j](j∈[l,r]且s[j]=x),直接枚举太慢不可取。
可以把原数组a[i]%k后的值进行排序,并记录每个数的左右界。这样每个询问就可以用二分在O(lgn)内完成。
总时间复杂度为O(n*lgn*lgn) 。用可持久化线段树同样可以做到。
更好的方法:
对于询问(l,r,x)来说,询问的答案为f[r][x]-f[l-1][x],f[r][x]表示s[1],s[2]到s[r]中等于x的个数,维护f很低效。
可以这样做:处理所有询问,每个询问(l,r,x)插入2条记录,一条插入记录(x,-1)到结点l-1的询问链表中,再插入(x,1)到结点r的询问链表中。
记录 cnt[x]表示前缀和为x的出现次数,从小到大枚举位置i,更新cnt[s[i]]++,扫描结点i的询问链表,对于其中的每一个记录(value,sign)更新答案ans+=cnt[value]*sign
均摊下来cost为O(e)。总时间复杂度为O(nlgn)。
一维分治4 :CF549F Yura and Developers
举例:N=4,序列为{4,3,2,5},K=3
枚举a[1],以a[1]为最大值的区间为[1,3],左部分小,枚举左边界L=1,右边界的区间是[2,3],增加一个询问(2,3,1),向结点1插入记录(1,-1),向结点3插入记录(1,1)
枚举a[2],以a[2]为最大值的区间为[2,3],左部分小,枚举左边界L=2,右边界的区间只能取[3,3],增加一个询问(3,3,1),向结点2插入记录(1,-1),向结点3插入记录(1,1)
枚举a[3],以a[3]为最大值的区间为[3,3],不需要考虑
枚举a[4],以a[4]为最大值的区间为[1,4],右部分小,枚举右边界R=4,左边界区间为[1,3],增加询问(0,2,0),向结点-1插入记录(0,-1),向结点2插入记录(0,1)
i -1 0 1 2 3 4
A[i] 0 0 4 3 2 5
L[i] 0 0 1 2 3 1
R[i] 0 0 3 3 3 4
A[i]%K 0 0 1 0 2 2
S[i]%K 0 0 1 1 0 2
-1
0
1
2
3
4
(1,-1)
(1,1)
(1,1)
(1,-1)
(0,-1)
(0,1)
一维分治4 :CF549F Yura and Developers
举例:N=4,序列为{4,3,2,5},K=3
一开始cnt[0]=cnt[1]=cnt[2]=0,ans=0
i=-1,cnt[]={1,0,0},枚举结点-1的询问链表,更新ans=-1
i=0,cnt[]={2,0,0},结点0后没有询问链表,ans保持不变
i=1,cnt[]={2,1,0},枚举结点1的询问链表,ans=ans+cnt[1]*-1=-2
i=2,cnt[]={2,2,0},枚举结点2的询问链表,ans=ans+cnt[1]*-1+cnt[0]*1=-2
i=3,cnt[]={3,2,0},枚举结点3的询问链表,ans=ans+cnt[1]*1+cnt[1]*1=2
i=4,cnt[]={3,2,1},结点4后没有询问链表,ans保持不变
Ans=2,对应的两个区间是[4,3]和[4,3,2,5]。
i -1 0 1 2 3 4
A[i] 0 0 4 3 2 5
L[i] 0 0 1 2 3 1
R[i] 0 0 3 3 3 4
A[i]%K 0 0 1 0 2 2
S[i]%K 0 0 1 1 0 2
-1
0
1
2
3
4
(1,-1)
(1,1)
(1,1)
(1,-1)
(0,-1)
(0,1)
一维分治5:计蒜之道 百度地图的实时路况
给一个有N(4<=N<=300)个点的无向图。定义d(x,y,z)为从x号点出发,严格不经过y号点,最终到达z号点的最短路径长度。如果这样的路径不存在,d(x,y,z)的值为-1.
求
一维分治5:计蒜之道 百度地图的实时路况
这题类似Floyd,但是是求不经过某个点的时候,所有点之间两两的最短路。
可以枚举不经过的点然后Floyd,时间复杂度为O(n^4)。
但是考虑到每个不经过的点的时候,其实有很多的两点之间的距离并不会改变,有重复计算。
分治:对于一个分治区间[l,r],我们会处理出一个最短路矩阵,表示不以[l,r]区间的点作为中转点的最短路。那么从[l,r]递归到[l,mid]只需要枚举[mid+1,r]的点作为k(中转点)在原矩阵的基础上跑Floyd,就能计算出[l,mid]对应的矩阵,[mid+1,r]也是同理在[l,r]最短路矩阵的基础上把[l,mid]中的点添加到允许经过的点中就可以计算出[mid+1,r]对应的矩阵。
最后分治区间长度为1的时候,就是不以对应点为中转点的最短路矩阵了。时间复杂度是O(n^3*lg n)。
二维分治1:CF480E Parking Lot
给出一个n×m(n,m<=2000)的网格图,有的位置上有障碍物。给出k(k<=2000)个操作,每次将一个格子变为障碍物,再询问没有障碍物的最大子正方形。
Time Limit: 3s
二维分治1:CF480E Parking Lot
定义f[i][j]表示以第i行第j列为右下角的最大子正方形的边长。
对于每次操作,利用动态规划f[i][j]=min{f[i-1][j-1],f[i-1][j],f[i][j-1]}+1
时间复杂度为O(nmk),超时。
可以用分治
定义f[L][R]表示原网格图第L行到第R行k次操作后的最大子正方形大小。
将矩阵尽可能分成上下相等的两部分。设中间一行为mid。
那么f[L][R]就是以下3部分的最大值。
①f[L,mid]
②f [mid+1,R]
③穿过mid这一行的最大子正方形
前两个可以分治递归求解。
二维分治1:CF480E Parking Lot
对于跨过中间mid一行的正方形:
每个格点维护up[i][j]和down[i][j],up[i][j]表示从位置(i,j)开始向上有多少个连续的无障碍的位置,down[i][j]表示从位置(i,j)开始向下有多少个连续的无障碍的位置,初始的up和down可以用递推在O(nm)内完成。
按顺序处理每个操作,对于每个在当前分治范围内的操作(x,y),只会影响第y列的up和down的值,在O(n)内更新这些值。
跨过中线的最大正方形,一定包含第mid行,考虑该正方形左边界为列号i,右边界为列号j。
先枚举左边界i,再枚举右边界j,则包含第x行第i列到第j列的矩形的宽度w=j-i+1,高度h=min_up+min_down-1,该情况下的最大子正方形的边长为min(w,h),其中min_up=min{up[mid][i],up[mid][i+1],…,up[mid][j]},min_down{down[mid][i],down[mid][i+1],…,down[mid][j]}
第mid行
第i列
第j列
min_up
min_down
二维分治1:CF480E Parking Lot
min_up和min_down的计算可以通过维护两个单调递增的队列来实现,因为是计算区间最小值,当后面出现更小的值时可以删除前面比该值大的元素, min_up和min_down的值分别在队列的第1个位置。
容易知道,宽度w在递增,高度h非递增,所以当h
每次递归返回的是k次操作后的子正方形大小,可能只有其中一部分操作在当前递归区间内,对于不在区间的操作直接赋为最靠近的前面一个操作后的答案,比如第x操作后的答案为value,下一次操作是y,则第x+1,x+2,…,y-1操作后的答案直接赋为value即可。
所以对于每次操作,计算跨过中间mid一行的正方形的大小可以在O(m)内完成,分治过程中对于每个操作最多有lgn的分治区间包含它。所以总时间复杂度为O((m+n)*k*lgn)。
min_up
min_down
二维分治1:CF480E Parking Lot
更好的方法:
离线处理,先把最后的答案用动态规划在O(n*m)完成。
从后往前做,每次相当于把一个障碍物变成非障碍物,答案肯定非递减。
对于操作(x,y),在O(n)内更新第y列的up和down的值。
如果答案增大,一定跟第x行有关系,所以我们就处理包含第x行的答案,处理方法跟前面计算跨过中线的答案一样,处理每个操作的时间复杂度为O(m)。
总时间复杂度是O(n*m+m*k)。
二维分治2:CF364E Empty Rectangle
给出一个n*m(1<=n,m ≤ 2500)的01网格,求有多少矩形中恰好包含k(0<=k<=6)个1。
Time Limit: 12s
二维分治2:CF364E Empty Rectangle
方法一:
初始化s[i][j]表示以(1,1)为左上角(i,j)为右下角的矩形中的元素之和
递推O(nm)内解决:s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j]
枚举左上角(x1,y1)和右下角(x2,y2)判断s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]是否等于k。
时间复杂度为(n^2*m^2)。超时。
方法二:
枚举左边界L,右边界R,下边界B,上边界是可以用二分计算出来。
时间复杂度为O(n*m^2*lgn)。
二维分治2:CF364E Empty Rectangle
方法三:分治法
像例1.10那样定义f[L][R]表示原矩阵第L行到第R行1的个数等于k的子矩阵的数量。
将矩阵尽可能均分成两部分。设中间一行为mid。
那么f[L][R]就是以下3部分的最大值。
①f[L,mid]
②f [mid+1,R]
③穿过mid这一行格点满足要求的子矩阵的数量,注意该矩阵必须包含第mid行和第mid+1行。
前两个可以分治递归求解。
二维分治2:CF364E Empty Rectangle
计算穿过第mid这一行的数量,可以枚举左边界i,再枚举右边界j
定义up[x]表示以i为左边界、j为右边界、mid为下边界的1的个数不超过x的最大矩形的上边界,则1的个数等于x的红色矩形有up[x-1] -up[x]个。同理定义down[x]表示以i为左边界、j为右边界、mid+1为上边界的1的个数不超过x的最大矩形的下边界,则1的个数等于x的绿色矩形有down[x]-down[x-1]个。
随着j的右移,up[x]是单调增的,down[x]是单调减的
统计答案:枚举x,ans+=(up[x-1]-up[x])*(down[k-x]-down[k-x-1]),具体实现要注意其他细节。
合并这一步操作时间复杂度为O(m*m*k)
T(n)=2*T(n/2)+m*m*k
T(n)=O(n*m*m*k)(注意与上题的区别!!)
mid
i
j
二维分治2:CF364E Empty Rectangle
T(n)=2*T(n/2)+m*m*k
=2*(2*T(n/4)+m*m*k)+m*m*k
=4*T(n/4)+2*m*m*k+m*m*k
=…
≈2*n*m*m*k=O(n*m*m*k)
n
n/2
n/2
n/4
n/4
n/4
n/4
1
1
1
1
1
1
1
1
m*m*k
2*m*m*k
4*m*m*k
n*m*m*k
lgn
二维分治2:CF364E Empty Rectangle
采用二维分治,横向划分和纵向划分相结合
递归树示意图如下:
总时间复杂度为O(k*(m*m*logn+n*n*logm))
也可以每次分成4块分治下去,时间复杂度一样。
m*m*k
m*m*k
n*n*k/2
n*n*k/2
点分治1:Poj1741 树中点对统计
给定一棵N(1<=N<=10000)个结点的带权树,定义为dis(u,v)为u,v两点间的最短路径长度,路径的长度定义为路径上所有边的权和。 再给定一个K(1<=K<=10^9),如果对于不同的两个结点a,b,满 足dis(a,b)<=K,则称(a,b)为合法点对。求合法点对个数。
点分治1:Poj1741 树中点对统计
方法一:
以每一个点为起点出发做DFS,统计出任意点对的最短路径长度,时间复杂度高达O(N^2)
方法二:
一条路径要么过根结点,要么在根结点的某一个子树中,可以用分治算法。
路径在子树中的情况递归处理即可,下面分析经过根结点的情况。
点分治1:Poj1741 树中点对统计
定义Depth(i)表示点i到根结点的路径长度,Belong(i)=X ( X 为根结点的某个儿子,且结点i在以X为根的子树内)。那么我们要统计的就是:
满足Depth(i)+Depth(j)<=K且Belong(i)≠Belong(j)的(i,j)个数
=满足Depth(i)+Depth(j)<=K的(i, j)个数–
满足Depth(i)+Depth(j)<=K且Belong(i)=Belong(j)的(i, j)个数
这两个部分都是要求满足Ai+Aj<=k的(i,j)的对数。可以将A排序后利用单调性我们很容易得出一个O(N)的算法,所以我们可以用O(NlogN)的时间来解决这个问题。
综上,此题使用分治算法的时间复杂度为 O(N*logN*递归深度) 。
点分治1:Poj1741 树中点对统计
递归深度取决于选择的根结点。
最佳选择是选一个点作为根结点,使得其结点最多的子树的结点数最小,也被称为“树的重心”,可以用树形DP在O(N)内求出。
定理:树的重心分出的子树的结点个数均不大于N/2。
证明:假设U是树的重心,它与V1,V2,…,Vk相邻,记Size(X)表示 以X为根的子树的结点个数。记V为V1,V2,…,Vk中Size值最大的点。 采取反证法,假设Size(V)>N/2,那么我们考虑如果选取V作为根结点的情况,记Size’(X)表示此时以X为根的子树的结点个数。 如下图,对于A部分,显然Size’(Ti)
每次递归选择子树的重心做为树根,max_i表示第i层的子树结点最多的结点数,有max_1<=N,max_2<=N/2,max_i<=N/(2^(i-1)),递归深度为O(logN)。
总时间复杂度为O(N*logN*logN)。
max_1<=N
max_2<=N/2
max_3<=N/4
O(logN)
点分治1:Poj1741 树中点对统计—代码
void solve(int u) //计算以u为根的子树中dis(a,b)<=K的点对数。
{
int G = calcG(u);//寻找树的重心G
vis[G] = true;
ans += calc(G, 0);//统计满足Depth(i)+Depth(j)<=K的(i, j)个数
for (int e = adj[G]; e; e = nxt[e])
if (!vis[go[e]]) ans -= calc(go[e], len[e]);
//统计满足Depth(i)+Depth(j)<=K且Belong(i)=Belong(j)的(i, j)个数
for (int e = adj[G]; e; e = nxt[e])
if (!vis[go[e]]) solve(go[e]);//递归处理G的子树
}
点分治1:Poj1741 树中点对统计—代码
long long calc(int sv, int L){ //计算以sv为根的子树中到根sv的距离<=K-L的结点数。
static int qn, que[N], d[N];
int u, v, e, d_n = 0;
que[qn = 1] = sv, dis[sv] = L, fa[sv] = 0;
for (int ql = 1; ql <= qn; ++ql) {
d[d_n++] = dis[u = que[ql]];
for (e = adj[u]; e; e = nxt[e]) {
if (vis[v = go[e]] || v == fa[u]) continue;fa[v] = u, dis[v] = dis[u] + len[e], que[++qn] = v;
}
}//宽搜
long long cnt = 0;
std::sort(d, d + d_n);
int l = 0, r = d_n - 1;
while (l < r) { if (d[l] + d[r] <= K) cnt += r - l++; else –r; }//使用双指针利用单调性统计答案。
return cnt;
}
点分治1:Poj1741 树中点对统计
也可以把前面已经完成的子树中的距离加入到平衡树,下一个子树中每计算出一个距离就到平衡树中统计答案,一个子树中全部处理完再加入到平衡树中。
常数更小的写法:
增加B[],B[x]记录x在root的哪个子结点的子树中,B[root]=root
计算经过根结点路径点对:“满足Depth(i)+Depth(j)<=K的(i, j)个数”–
“满足Depth(i)+Depth(j)<=K且Belong(i)=Belong(j)的(i, j)个数”时,可以不用多次调用clac()。直接把树中的点都取出来放进数组中,按照D[x]递增排序。
还是用两个指针 i, j ,i从左开始枚举,表示路径到root距离较小的端点,j从后向前开始扫描数组,可以计算出满足D[x]+D[y]<=k的合法点对(x,y)的个数,其中x、y分别是i、j指向的节点编号。
计算方法如下:
设F[i]表示在左、右指针中间满足B[x]=i的点x的个数,先初始化F[],枚举过程中i向右加1前先执行F[B[node[i]]]--,j减1前线执行F[B[node[j]]]-- 。
设当前左指针指向点x,则 j-i-F[B[x]] 就是要求的答案。
排序是O(NlogN)的,扫描是O(N)的。总时间复杂度还是O(N*logN*logN),但常数减小。
点分治2: CF293E Close Vertices
给一棵N个顶点的树,求有多少条路径的边数不超过L,且边权和小于等于W。
1 ≤ N ≤ 105 1 ≤ L ≤ N 0 ≤ W ≤ 109
Time Limit: 3s
点分治2: CF293E Close Vertices
用树分治,比上题多边数限制。做法与上一题类似:
把路径分成两类:
①在根的子结点为根的子树中,递归处理即可;
②路径经过根结点
②的处理方法跟上题代码中一样,等于calc(root,0)-∑calc(son_i,edge(root,son_i))
计算calc()时,一样按照到根结点root的距离从小到大排序,从右往左一个端点i,另外一个端点j从小到大递增,j每次向右移,就把新加入的结点node[j]对应的num[node[j]](到根结点的边数)添加到树状数组中,再统计数状数组中<=W-num[node[i]]的个数即可。
总时间复杂度是O(N*logN*logN)。
点分治3:WC2010重建计划
给出一棵N个节点带权树。
求边数在[L,R]之间的所有路径中,最大的权值平均值。
N ≤ 100000
点分治3:WC2010重建计划
二分答案mid,将图中所有边减mid,问题转换为判断是否存在边数为x的路径,路径边权和>=0,L<=x<=R。
对于递归执行的每棵树,先找出重心,从重心剖开树以后,得到若干棵子树
顺序处理每棵子树,对于一棵子树,Bfs得其所有路径边数及边权和(起点从重心出发,终点在该子树内),由于是Bfs,所以路径长度是从小到大
并维护mx[i]表示起点从重心出发,终点在子树内,长度为i的路径边权和最值,当前正在处理的子树中的信息先不添加到mx[]中,处理完再把这些信息更新到mx[]中
Bfs处理子树中路径i,路径i的长度为x,则需要维护mx中长度在区间[L-x,R-x]内的最大值,该区间是向左平移的,可以维护单调递减队列。
时间复杂度为O(N*logN*logN)。
同课章节目录
