19.1.1平行四边形的性质(2)(广东省湛江市霞山区20中)
文档属性
| 名称 | 19.1.1平行四边形的性质(2)(广东省湛江市霞山区20中) |  | |
| 格式 | rar | ||
| 文件大小 | 777.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-03 16:16:00 | ||
图片预览

文档简介
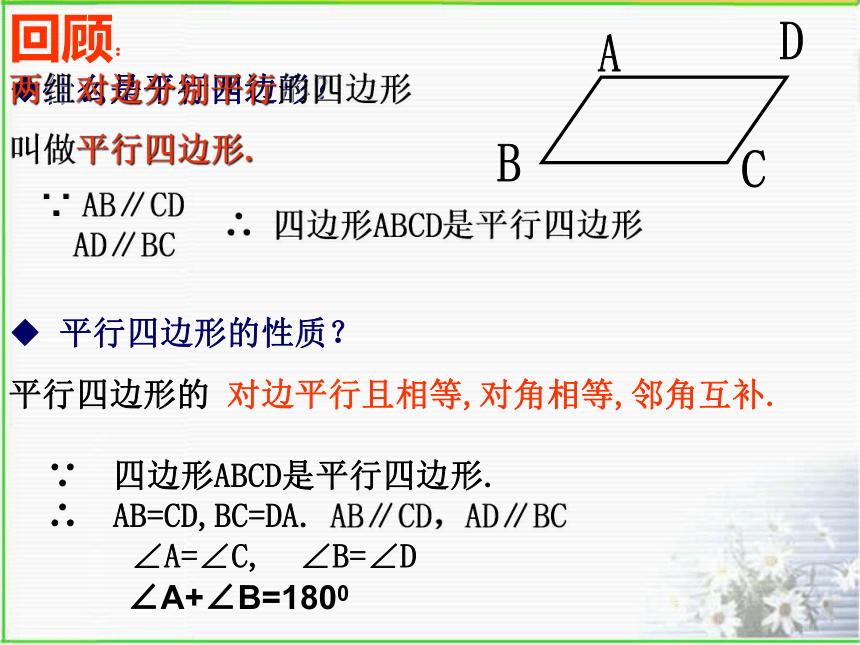
课件11张PPT。平行四边形的性质(2)授课人:沈海尉回顾:◆什么是平行四边形?◆ 平行四边形的性质?两组对边分别平行的四边形
叫做平行四边形. ∴ 四边形ABCD是平行四边形∵ AB∥CD
AD∥BC平行四边形的 对边平行且相等,对角相等,邻角互补.∵ 四边形ABCD是平行四边形.
∴ AB=CD,BC=DA.
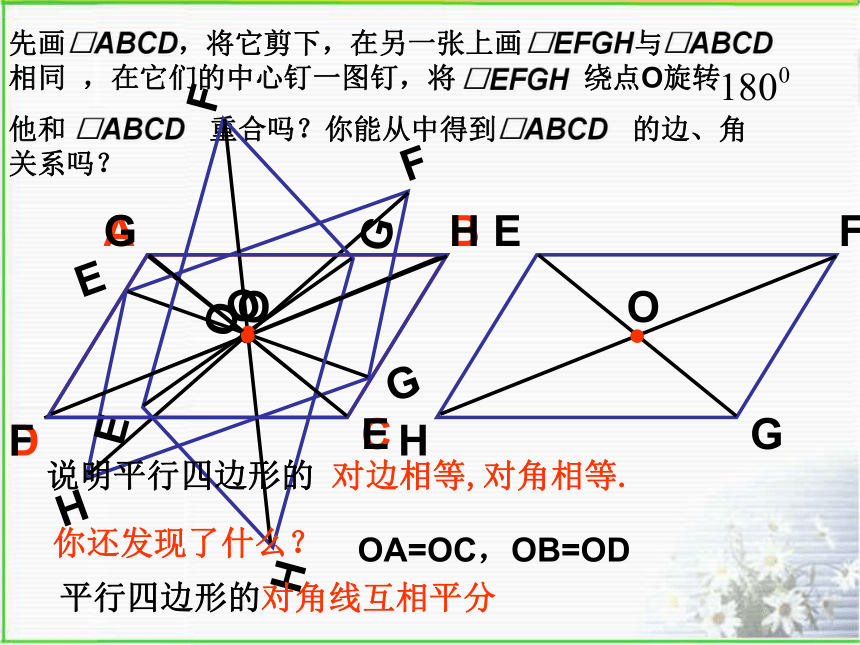
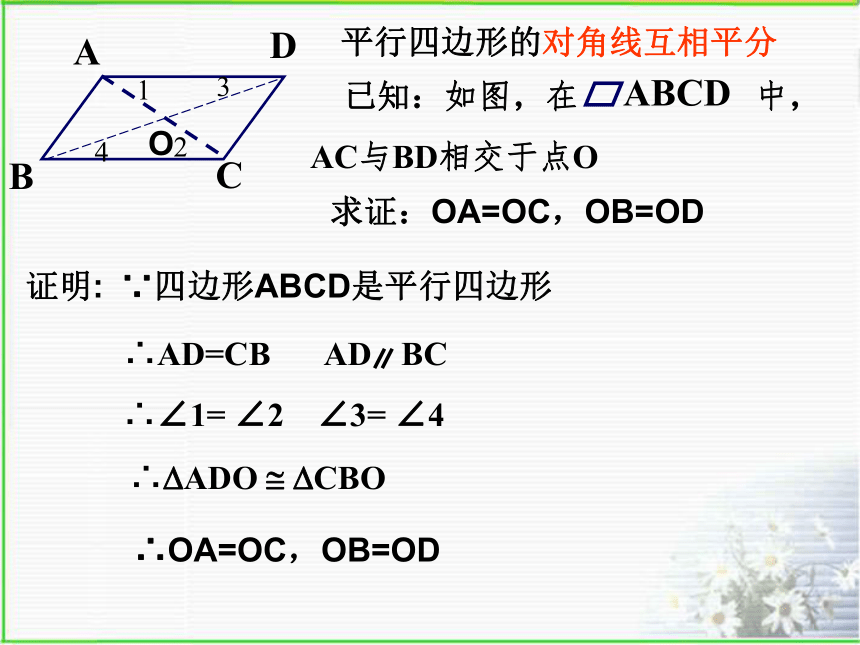
∠A=∠C, ∠B=∠DAB∥CD,AD∥BC∠A+∠B=1800说明平行四边形的 对边相等,对角相等.你还发现了什么?OA=OC,OB=OD 平行四边形的对角线互相平分 已知:如图,在 中,
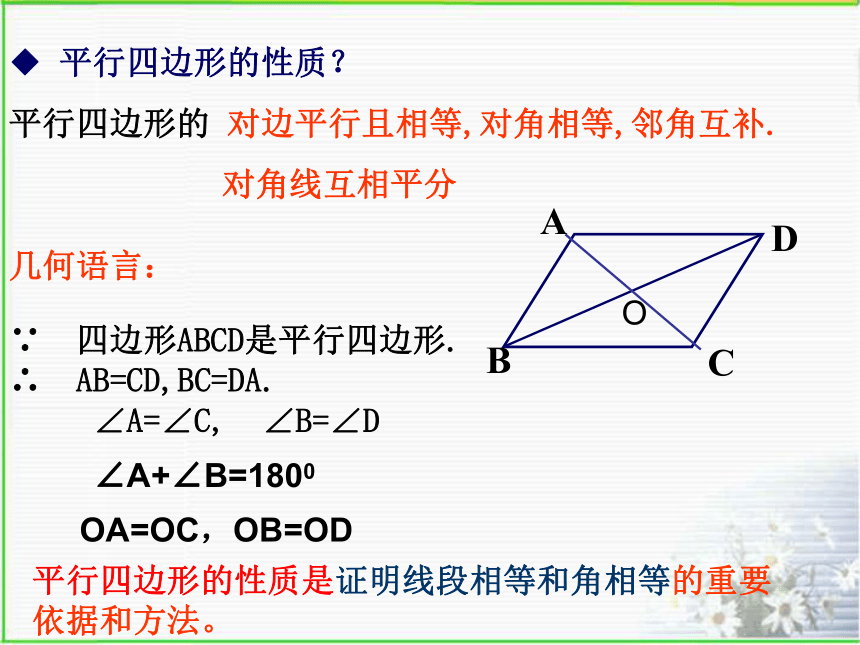
AC与BD相交于点OABCD1234O ∴∠1= ∠2∠3= ∠4 ∴?ADO ? ?CBO ∴AD=CB求证:OA=OC,OB=OD ∵四边形ABCD是平行四边形∴OA=OC,OB=OD 证明:平行四边形的对角线互相平分◆ 平行四边形的性质?平行四边形的 对边平行且相等,对角相等,邻角互补.对角线互相平分几何语言:O∵ 四边形ABCD是平行四边形.
∴ AB=CD,BC=DA.
∠A=∠C, ∠B=∠D∠A+∠B=1800OA=OC,OB=OD 平行四边形的性质是证明线段相等和角相等的重要依据和方法。例题1:如图,四边形ABCD是平行四边形,AB=10,AD=8,DB⊥AD,求BC,CD及OB的长及 □ ABCD 的面积.解;∵四边形ABCD是平行四边形∴OB= BD=3∴BD= = =6,在Rt△ADB中,AD=8,AB=10,∴BC=AD=8,CD=AB=10□ ABCD如图: 在?ABC中,AD平分∠BAC,点M,E,F分别是 AB,AD,AC上的点,四边形BEFM是平行四边形.
求证:AF=BM∴ AF=BM∴ AF=EF∴∠CAD =∠AEF∴ ∠BAD=∠AEF∵AB//EF∴∠BAD=∠CAD∵ AD平分∠BAC∴BM=EF AB//EF证明: ∵ 四边形BEFM是平行四边形ABDCO解:在□ ABCD中在△AOB中BO-AO<AB<AO+BO既1 <AB <11
如图,M是 ABCD边AD上任一点,若 △CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S,S1,S2之间有什么样的关系,并说明理由.1、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
2、已知, ABCD的周长是28,对角线AC,BD相交于点O,且△OAB的周长比△OBC的周长大4,则AB=
3、已知P为 ABCD的边CD上的任意点,则S△APB与S ABCD的比为
4、如图:P是 ABCD内的
一点, ,则 =创新演练S△APBS△CPDAD91:2
叫做平行四边形. ∴ 四边形ABCD是平行四边形∵ AB∥CD
AD∥BC平行四边形的 对边平行且相等,对角相等,邻角互补.∵ 四边形ABCD是平行四边形.
∴ AB=CD,BC=DA.
∠A=∠C, ∠B=∠DAB∥CD,AD∥BC∠A+∠B=1800说明平行四边形的 对边相等,对角相等.你还发现了什么?OA=OC,OB=OD 平行四边形的对角线互相平分 已知:如图,在 中,
AC与BD相交于点OABCD1234O ∴∠1= ∠2∠3= ∠4 ∴?ADO ? ?CBO ∴AD=CB求证:OA=OC,OB=OD ∵四边形ABCD是平行四边形∴OA=OC,OB=OD 证明:平行四边形的对角线互相平分◆ 平行四边形的性质?平行四边形的 对边平行且相等,对角相等,邻角互补.对角线互相平分几何语言:O∵ 四边形ABCD是平行四边形.
∴ AB=CD,BC=DA.
∠A=∠C, ∠B=∠D∠A+∠B=1800OA=OC,OB=OD 平行四边形的性质是证明线段相等和角相等的重要依据和方法。例题1:如图,四边形ABCD是平行四边形,AB=10,AD=8,DB⊥AD,求BC,CD及OB的长及 □ ABCD 的面积.解;∵四边形ABCD是平行四边形∴OB= BD=3∴BD= = =6,在Rt△ADB中,AD=8,AB=10,∴BC=AD=8,CD=AB=10□ ABCD如图: 在?ABC中,AD平分∠BAC,点M,E,F分别是 AB,AD,AC上的点,四边形BEFM是平行四边形.
求证:AF=BM∴ AF=BM∴ AF=EF∴∠CAD =∠AEF∴ ∠BAD=∠AEF∵AB//EF∴∠BAD=∠CAD∵ AD平分∠BAC∴BM=EF AB//EF证明: ∵ 四边形BEFM是平行四边形ABDCO解:在□ ABCD中在△AOB中BO-AO<AB<AO+BO既1 <AB <11
如图,M是 ABCD边AD上任一点,若 △CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S,S1,S2之间有什么样的关系,并说明理由.1、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
2、已知, ABCD的周长是28,对角线AC,BD相交于点O,且△OAB的周长比△OBC的周长大4,则AB=
3、已知P为 ABCD的边CD上的任意点,则S△APB与S ABCD的比为
4、如图:P是 ABCD内的
一点, ,则 =创新演练S△APBS△CPDAD91:2
