人教版九年级数学上册第二十二章22.1二次函数图像和性质课堂达标练习题(含解析)
文档属性
| 名称 | 人教版九年级数学上册第二十二章22.1二次函数图像和性质课堂达标练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 356.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 22:24:38 | ||
图片预览




文档简介
人教版九年级数学上册第二十二章22.1二次函数图像和性质课堂达标练习题
一、选择题
1.下列函数中,属于关于的二次函数的是( )
A. B.
C. D.
2.已知二次函数的图象开口向下,则的取值范同是( ).
A. B. C. D.
3.抛物线的顶点、对称轴分别是( )
A., B.,
C., D.,
4.如图所示,抛物线的顶点坐标是,则函数值随自变量的增大而减小的的取值范围是( ).
A. B. C. D.
5.当函数 是二次函数时, 的取值为( )
A. B. C. D.
6.若,,则与的大小关系为( )
A. B. C. D.
7.设是拋物线上的三点,则的大小关系为( )
A. B.
C. D.
8.函数和为常数,且,在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
9.二次函数y=ax2+bx+c(a≠0)的部分对应值列表如表:
x …… -1 0 1 3 5 ……
y …… -5 -8 -9 -5 7 ……
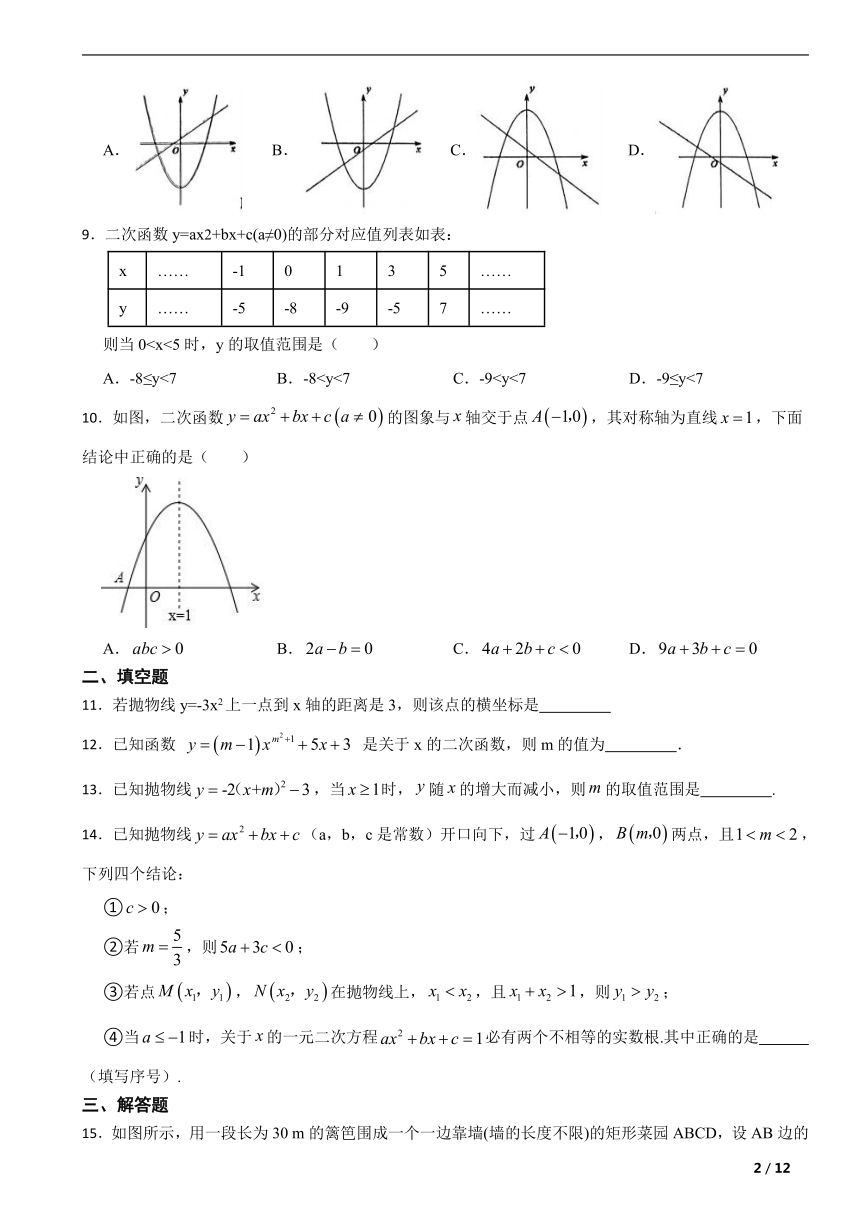
则当0A.-8≤y<7 B.-810.如图,二次函数的图象与轴交于点,其对称轴为直线,下面结论中正确的是( )
A. B. C. D.
二、填空题
11.若抛物线y=-3x2上一点到x轴的距离是3,则该点的横坐标是
12.已知函数 是关于x的二次函数,则m的值为 .
13.已知抛物线,当时,随的增大而减小,则的取值范围是 .
14.已知抛物线(a,b,c是常数)开口向下,过,两点,且,下列四个结论:
①;
②若,则;
③若点,在抛物线上,,且,则;
④当时,关于的一元二次方程必有两个不相等的实数根.其中正确的是 (填写序号).
三、解答题
15.如图所示,用一段长为30 m的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边的长为.求:
(1)菜园的面积关于的函数表达式.
(2)自变量的取值范围.
16.请直接写出二次函数y=(x﹣1)2+2图象的开口方向、对称轴和顶点坐标.
17.如图所示,抛物线经过两点,交轴于点C,D为抛物线的顶点,连结BD,H为BD的中点.请在轴上找一点,使的值最小,并求的最小值.
四、综合题
18.如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为ts,四边形APQC的面积为ymm2.
(1)y与t之间的函数关系式;
(2)求自变量t的取值范围;
(3)四边形APQC的面积能否等于172mm2.若能,求出运动的时间;若不能,说明理由.
19.已知 是二次函数,且当x>0时,y随着x的增大而增大.
(1)求k的值;
(2)求顶点坐标和对称轴.
20.已知函数
(1)若图象与x轴的交点为A、B,与y轴的交点C,求△ABC的面积;
(2)直接回答:①当x取何值时,函数值大于0?②当x取何值时,函数值y随x的增大而增大?
21.二次函数的图像经过,两点.
(1)当时,判断与的大小.
(2)当时,求的取值范围.
(3)若此函数图象还经过点,且,求证:.
答案解析部分
1.【答案】D
【解析】【解答】解:A、x=y2,y不是x的函数,该选项不符合题意;
B、,不是整式,所以y不是x的二次函数,该选项不符合题意;
C、,y是x的一次函数,该选项不符合题意;
D、 ,y是x的二次函数,该选项符合题意;
故答案为:D。
【分析】用自变量的二次整式来表示的函数就是二次函数,
2.【答案】D
【解析】【解答】解: ∵二次函数的图象开口向下,
∴2-a<0,
∴a>2,
故答案为:D.
【分析】 二次函数(a≠0)中,当a>0时开口向下,当a<0时开口向下 ,据此解答即可.
3.【答案】C
【解析】【解答】解:∵y=2(x-1)2-3,
∴抛物线的顶点坐标为(1,-3),对称轴为直线x=1.
故答案为:C.
【分析】根据顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是直线x=h.
4.【答案】C
【解析】【解答】解:∵抛物线的开口向下,
∴在对称轴右侧y随x的增大而减小,
∵该函数的顶点坐标为P(1,3),
∴该抛物线的对称轴直线为x=1,
∴当x≥1时,函数值y随自变量x的增大而减小.
故答案为:C.
【分析】二次函数的图象与性质:二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,若a<0,图象开口向下,对称轴直线为x=,顶点坐标为(,),则当x≤时,y随x的增大而减增大;当x≥时,y随x的增大而减小;当x=时,y达到最大值,y=,无最小值,据此可作答.
5.【答案】D
【解析】【解答】解:∵函数 是二次函数,
∴a-1≠0, =2,
∴a≠1, ,
∴ ,
故答案为:D.
【分析】形如“y=ax2+bx+c (a,b,c都是常数,且a≠0)”的函数,就是二次函数,根据定义列出混合组,求解即可.
6.【答案】C
7.【答案】B
【解析】【解答】 拋物线 的图象开口向下,对称轴为x=-2,图象有最大值,
根据三点的横坐标,得知:
C距离对称轴最远,故y3最小
B距离对称轴最近,故y2最大
A距离对称轴居中间,故y1也居中间
故选:B
【分析】根据二次函数图象的性质,开口向下有最大值,距离对称轴越近的点的函数值越大,据此可以判定。
8.【答案】C
【解析】【解答】 假设a0,的图象是开口向上、y轴是对称轴、顶点在y轴正半轴的抛物线,
函数 的图象是经过一、三、二象限的一条直线;
假设a0,的图象是开口向下、y轴是对称轴、顶点在y轴正半轴的抛物线,
函数 的图象是经过二、四、一象限的一条直线.
由此判定如下:
A、抛物线开口向上,但顶点在负半轴,不符合题意;
B、抛物线开口向上,但顶点在负半轴且直线过第四象限,不符合题意;
C、抛物线开口向下,顶点在正半轴,直线过二、一、四象限,符合题意;
D、抛物线开口向下,顶点在正半轴,但直线过第三象限,不符合题意。
故选:C
【分析】掌握一次函数和二次函数的图象的性质,找到各选项图中矛盾之处即可找出正确选项。最简洁的思路是:根据抛物线交y轴于正半轴排除AB,正确答案在CD中,a小于0,-a大于0,直线交y轴于正半轴,故选C.
9.【答案】D
【解析】【解答】解:由表格中的数据可得当和时,函数值相等,
二次函数的对称轴是直线,
当时,函数有最小值-9,
当时,函数值为-8,当时,函数值为7,
当时,y的取值范围是.
故答案为:D.
【分析】由表格中的数据可得当x=-1和x=3时,函数值相等,根据二次函数的轴对称性可得二次函数的对称轴是直线x=1,故当x=1时,函数有最小值-9,进而可得当010.【答案】D
【解析】【解答】解:
解:A、函数的对称轴在y轴右侧,则ab<0,而c>0,故abc<0,故原答案错误,不符合题意;
B、函数的对称轴为:x==1,故2a-b=0,错误,不符合题意;
C、图象与x轴交于点A(-1,0),其对称轴为直线x=1,则图象与x轴另外一个交点坐标为:(3,0),故当x=2时,y=4a+2b+c>0,故原答案错误,不符合题意;
D、图象与x轴另外一个交点坐标为:(3,0),即x=3时,y=9a+3b+c=0,正确,符合题意;
故答案为:D.
【分析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
11.【答案】1或-1
【解析】【解答】解:∵抛物线y=-3x2的开口向下,抛物线上一点到x轴的距离是3,
∴这点的纵坐标为-3,
当y=-3时,-3x2=-3,
∴x=1或-1.
故答案为:1或-1.
【分析】根据题意求出当-3时x的值,即可得出答案.
12.【答案】﹣1
【解析】【解答】解:根据题意得: ,
解得:m=﹣1.
故答案是:﹣1.
【分析】根据二次函数的定义列出不等式求解即可.
13.【答案】
【解析】【解答】解: ∵y=-2 (x+m) 2-3,
∴对称轴为x=-m,
∵a=-2<0,
∴抛物线开口向下,
∴在对称轴右侧y随x的增大而减小,
∵当x≥1时,y随x的增大而减小,
∴-m≤1,解得m≥-1,
故答案为:m≥-1.
【分析】根据顶点式可判断抛物线的开口与对称轴,从而可得关于m的不等式,求解即可.
14.【答案】①③④
15.【答案】(1)解:设AB的长为x(m),则AD的长为:(m),
由题意可得,;
(2)解:由于强的长度不限,
∴,
解得.
【解析】【分析】(1)根据篱笆的总长结合图形用含x的式子表示出AD的长,进而根据矩形的面积计算公式建立出y关于x的函数解析式;
(2)由于强的长度不限,故自变量的取值范围只有保证矩形的边长为正数即可,据此列出不等式组,求解即可.
16.【答案】解:∵y=(x-1)2+2,
∴该函数的开口向上,对称轴是直线x=1,顶点坐标为(1,2)
【解析】【分析】已知函数解析式是顶点式,直接利用抛物线的解析式求出开口方向、对称轴和顶点坐标。
17.【答案】解:抛物线过点,
解得
拋物线的函数表达式为.
,
顶点的坐标为.
点,
中点的坐标为,其关于轴的对称点的坐标为.
连结与轴相交于点,则此时最小,
且最小值为
【解析】【分析】将点A,B的坐标代入函数解析式,可求出b,c的值,再将函数解析式转化为顶点式,可得到点D的坐标;再求出点H的坐标,利用关于y轴对称的点的坐标特点,可求出点H′的坐标,连结与轴相交于点,则此时最小;然后利用平面直角坐标系中,两点间的距离公式求出其最小值.
18.【答案】(1)解:∵出发时间为t,点P的速度为2mm/s,点Q的速度为4mm/s,
∴PB=12﹣2t,BQ=4t,
∴y= ×12×24﹣ ×(12﹣2t)×4t
=4t2﹣24t+144.
(2)解:∵t>0,12﹣2t>0,
∴0<t<6.
(3)解:不能,
4t2﹣24t+144=172,
解得:t1=7,t2=﹣1(不合题意,舍去)
因为0<t<6.所以t=7不在范围内,
所以四边形APQC的面积不能等于172mm2.
【解析】【分析】(1)利用两个直角三角形的面积差求得答案即可;(2)利用线段的长度与运动速度建立不等式得出答案即可;(3)利用(1)的函数建立方程求解判断即可.
19.【答案】(1)解:由y=(k+2) 是二次函数,且当x>0时,
y随x的增大而增大,得
解得k=2;
(2)解:y=4x2的顶点坐标是(0,0),对称轴是y轴.
【解析】【分析】(1)根据二次函数y=ax2(a≠0)的次数是2,列出关于k的方程,结合二次函数图象的性质,得出k+2>0,即可;
(2)根据二次函数y=ax2(a≠0)图象的性质,可得顶点坐标、对称轴,即可解答.
20.【答案】(1)解:令 =0,
解得:x1=1,x2=-3,
∴A(1,0),B(-3,0),
∴AB=1-(-3)=4,
令x=0,y=-3,
∴C(0,-3),
∴OC=3,
∴ △ABC的面积=AB×OA=×4×3=6.
(2)解:∵ =x2+2x-3,
看图象可知,当 x<3或x>1时, 函数值大于0 ,
∵对称轴x=-1,图象的开口向上,
∴ x>-1时, 函数值y随x的增大而增大 .
【解析】【分析】(1)分别令x=0和y=0,求出图象与x轴和y轴的交点坐标,再求出AB和OC长,然后根据三角形面积公式计算即可;
(2)画出函数图象,看图象找出在x轴上方部分的x的范围,即函数值大于0时,x的范围,求出对称轴,看图即可在对称轴右方函数值y随x的增大而增大 .
21.【答案】(1)解:当时,
,
,
(2)解:,
又,
,
;
(3)证明:二次函数的对称轴为直线,
二次函数经过两点,
,即,
,
【解析】【分析】(1)当b=1时,y1=6+c,y2=c,据此进行比较;
(2)分别将x=-2、x=1代入可得y1=4+2b+c,y2=1-b+c,根据y1(3)根据二次函数的解析式可得对称轴为直线x=,由图象过(-2,y1)、(m,y1)两点可得|2|+=m-,则m=2+b,结合b的范围可得m的范围.
1 / 1
一、选择题
1.下列函数中,属于关于的二次函数的是( )
A. B.
C. D.
2.已知二次函数的图象开口向下,则的取值范同是( ).
A. B. C. D.
3.抛物线的顶点、对称轴分别是( )
A., B.,
C., D.,
4.如图所示,抛物线的顶点坐标是,则函数值随自变量的增大而减小的的取值范围是( ).
A. B. C. D.
5.当函数 是二次函数时, 的取值为( )
A. B. C. D.
6.若,,则与的大小关系为( )
A. B. C. D.
7.设是拋物线上的三点,则的大小关系为( )
A. B.
C. D.
8.函数和为常数,且,在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
9.二次函数y=ax2+bx+c(a≠0)的部分对应值列表如表:
x …… -1 0 1 3 5 ……
y …… -5 -8 -9 -5 7 ……
则当0
A. B. C. D.
二、填空题
11.若抛物线y=-3x2上一点到x轴的距离是3,则该点的横坐标是
12.已知函数 是关于x的二次函数,则m的值为 .
13.已知抛物线,当时,随的增大而减小,则的取值范围是 .
14.已知抛物线(a,b,c是常数)开口向下,过,两点,且,下列四个结论:
①;
②若,则;
③若点,在抛物线上,,且,则;
④当时,关于的一元二次方程必有两个不相等的实数根.其中正确的是 (填写序号).
三、解答题
15.如图所示,用一段长为30 m的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边的长为.求:
(1)菜园的面积关于的函数表达式.
(2)自变量的取值范围.
16.请直接写出二次函数y=(x﹣1)2+2图象的开口方向、对称轴和顶点坐标.
17.如图所示,抛物线经过两点,交轴于点C,D为抛物线的顶点,连结BD,H为BD的中点.请在轴上找一点,使的值最小,并求的最小值.
四、综合题
18.如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为ts,四边形APQC的面积为ymm2.
(1)y与t之间的函数关系式;
(2)求自变量t的取值范围;
(3)四边形APQC的面积能否等于172mm2.若能,求出运动的时间;若不能,说明理由.
19.已知 是二次函数,且当x>0时,y随着x的增大而增大.
(1)求k的值;
(2)求顶点坐标和对称轴.
20.已知函数
(1)若图象与x轴的交点为A、B,与y轴的交点C,求△ABC的面积;
(2)直接回答:①当x取何值时,函数值大于0?②当x取何值时,函数值y随x的增大而增大?
21.二次函数的图像经过,两点.
(1)当时,判断与的大小.
(2)当时,求的取值范围.
(3)若此函数图象还经过点,且,求证:.
答案解析部分
1.【答案】D
【解析】【解答】解:A、x=y2,y不是x的函数,该选项不符合题意;
B、,不是整式,所以y不是x的二次函数,该选项不符合题意;
C、,y是x的一次函数,该选项不符合题意;
D、 ,y是x的二次函数,该选项符合题意;
故答案为:D。
【分析】用自变量的二次整式来表示的函数就是二次函数,
2.【答案】D
【解析】【解答】解: ∵二次函数的图象开口向下,
∴2-a<0,
∴a>2,
故答案为:D.
【分析】 二次函数(a≠0)中,当a>0时开口向下,当a<0时开口向下 ,据此解答即可.
3.【答案】C
【解析】【解答】解:∵y=2(x-1)2-3,
∴抛物线的顶点坐标为(1,-3),对称轴为直线x=1.
故答案为:C.
【分析】根据顶点式y=a(x-h)2+k,顶点坐标是(h,k),对称轴是直线x=h.
4.【答案】C
【解析】【解答】解:∵抛物线的开口向下,
∴在对称轴右侧y随x的增大而减小,
∵该函数的顶点坐标为P(1,3),
∴该抛物线的对称轴直线为x=1,
∴当x≥1时,函数值y随自变量x的增大而减小.
故答案为:C.
【分析】二次函数的图象与性质:二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,若a<0,图象开口向下,对称轴直线为x=,顶点坐标为(,),则当x≤时,y随x的增大而减增大;当x≥时,y随x的增大而减小;当x=时,y达到最大值,y=,无最小值,据此可作答.
5.【答案】D
【解析】【解答】解:∵函数 是二次函数,
∴a-1≠0, =2,
∴a≠1, ,
∴ ,
故答案为:D.
【分析】形如“y=ax2+bx+c (a,b,c都是常数,且a≠0)”的函数,就是二次函数,根据定义列出混合组,求解即可.
6.【答案】C
7.【答案】B
【解析】【解答】 拋物线 的图象开口向下,对称轴为x=-2,图象有最大值,
根据三点的横坐标,得知:
C距离对称轴最远,故y3最小
B距离对称轴最近,故y2最大
A距离对称轴居中间,故y1也居中间
故选:B
【分析】根据二次函数图象的性质,开口向下有最大值,距离对称轴越近的点的函数值越大,据此可以判定。
8.【答案】C
【解析】【解答】 假设a0,的图象是开口向上、y轴是对称轴、顶点在y轴正半轴的抛物线,
函数 的图象是经过一、三、二象限的一条直线;
假设a0,的图象是开口向下、y轴是对称轴、顶点在y轴正半轴的抛物线,
函数 的图象是经过二、四、一象限的一条直线.
由此判定如下:
A、抛物线开口向上,但顶点在负半轴,不符合题意;
B、抛物线开口向上,但顶点在负半轴且直线过第四象限,不符合题意;
C、抛物线开口向下,顶点在正半轴,直线过二、一、四象限,符合题意;
D、抛物线开口向下,顶点在正半轴,但直线过第三象限,不符合题意。
故选:C
【分析】掌握一次函数和二次函数的图象的性质,找到各选项图中矛盾之处即可找出正确选项。最简洁的思路是:根据抛物线交y轴于正半轴排除AB,正确答案在CD中,a小于0,-a大于0,直线交y轴于正半轴,故选C.
9.【答案】D
【解析】【解答】解:由表格中的数据可得当和时,函数值相等,
二次函数的对称轴是直线,
当时,函数有最小值-9,
当时,函数值为-8,当时,函数值为7,
当时,y的取值范围是.
故答案为:D.
【分析】由表格中的数据可得当x=-1和x=3时,函数值相等,根据二次函数的轴对称性可得二次函数的对称轴是直线x=1,故当x=1时,函数有最小值-9,进而可得当0
【解析】【解答】解:
解:A、函数的对称轴在y轴右侧,则ab<0,而c>0,故abc<0,故原答案错误,不符合题意;
B、函数的对称轴为:x==1,故2a-b=0,错误,不符合题意;
C、图象与x轴交于点A(-1,0),其对称轴为直线x=1,则图象与x轴另外一个交点坐标为:(3,0),故当x=2时,y=4a+2b+c>0,故原答案错误,不符合题意;
D、图象与x轴另外一个交点坐标为:(3,0),即x=3时,y=9a+3b+c=0,正确,符合题意;
故答案为:D.
【分析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
11.【答案】1或-1
【解析】【解答】解:∵抛物线y=-3x2的开口向下,抛物线上一点到x轴的距离是3,
∴这点的纵坐标为-3,
当y=-3时,-3x2=-3,
∴x=1或-1.
故答案为:1或-1.
【分析】根据题意求出当-3时x的值,即可得出答案.
12.【答案】﹣1
【解析】【解答】解:根据题意得: ,
解得:m=﹣1.
故答案是:﹣1.
【分析】根据二次函数的定义列出不等式求解即可.
13.【答案】
【解析】【解答】解: ∵y=-2 (x+m) 2-3,
∴对称轴为x=-m,
∵a=-2<0,
∴抛物线开口向下,
∴在对称轴右侧y随x的增大而减小,
∵当x≥1时,y随x的增大而减小,
∴-m≤1,解得m≥-1,
故答案为:m≥-1.
【分析】根据顶点式可判断抛物线的开口与对称轴,从而可得关于m的不等式,求解即可.
14.【答案】①③④
15.【答案】(1)解:设AB的长为x(m),则AD的长为:(m),
由题意可得,;
(2)解:由于强的长度不限,
∴,
解得.
【解析】【分析】(1)根据篱笆的总长结合图形用含x的式子表示出AD的长,进而根据矩形的面积计算公式建立出y关于x的函数解析式;
(2)由于强的长度不限,故自变量的取值范围只有保证矩形的边长为正数即可,据此列出不等式组,求解即可.
16.【答案】解:∵y=(x-1)2+2,
∴该函数的开口向上,对称轴是直线x=1,顶点坐标为(1,2)
【解析】【分析】已知函数解析式是顶点式,直接利用抛物线的解析式求出开口方向、对称轴和顶点坐标。
17.【答案】解:抛物线过点,
解得
拋物线的函数表达式为.
,
顶点的坐标为.
点,
中点的坐标为,其关于轴的对称点的坐标为.
连结与轴相交于点,则此时最小,
且最小值为
【解析】【分析】将点A,B的坐标代入函数解析式,可求出b,c的值,再将函数解析式转化为顶点式,可得到点D的坐标;再求出点H的坐标,利用关于y轴对称的点的坐标特点,可求出点H′的坐标,连结与轴相交于点,则此时最小;然后利用平面直角坐标系中,两点间的距离公式求出其最小值.
18.【答案】(1)解:∵出发时间为t,点P的速度为2mm/s,点Q的速度为4mm/s,
∴PB=12﹣2t,BQ=4t,
∴y= ×12×24﹣ ×(12﹣2t)×4t
=4t2﹣24t+144.
(2)解:∵t>0,12﹣2t>0,
∴0<t<6.
(3)解:不能,
4t2﹣24t+144=172,
解得:t1=7,t2=﹣1(不合题意,舍去)
因为0<t<6.所以t=7不在范围内,
所以四边形APQC的面积不能等于172mm2.
【解析】【分析】(1)利用两个直角三角形的面积差求得答案即可;(2)利用线段的长度与运动速度建立不等式得出答案即可;(3)利用(1)的函数建立方程求解判断即可.
19.【答案】(1)解:由y=(k+2) 是二次函数,且当x>0时,
y随x的增大而增大,得
解得k=2;
(2)解:y=4x2的顶点坐标是(0,0),对称轴是y轴.
【解析】【分析】(1)根据二次函数y=ax2(a≠0)的次数是2,列出关于k的方程,结合二次函数图象的性质,得出k+2>0,即可;
(2)根据二次函数y=ax2(a≠0)图象的性质,可得顶点坐标、对称轴,即可解答.
20.【答案】(1)解:令 =0,
解得:x1=1,x2=-3,
∴A(1,0),B(-3,0),
∴AB=1-(-3)=4,
令x=0,y=-3,
∴C(0,-3),
∴OC=3,
∴ △ABC的面积=AB×OA=×4×3=6.
(2)解:∵ =x2+2x-3,
看图象可知,当 x<3或x>1时, 函数值大于0 ,
∵对称轴x=-1,图象的开口向上,
∴ x>-1时, 函数值y随x的增大而增大 .
【解析】【分析】(1)分别令x=0和y=0,求出图象与x轴和y轴的交点坐标,再求出AB和OC长,然后根据三角形面积公式计算即可;
(2)画出函数图象,看图象找出在x轴上方部分的x的范围,即函数值大于0时,x的范围,求出对称轴,看图即可在对称轴右方函数值y随x的增大而增大 .
21.【答案】(1)解:当时,
,
,
(2)解:,
又,
,
;
(3)证明:二次函数的对称轴为直线,
二次函数经过两点,
,即,
,
【解析】【分析】(1)当b=1时,y1=6+c,y2=c,据此进行比较;
(2)分别将x=-2、x=1代入可得y1=4+2b+c,y2=1-b+c,根据y1
1 / 1
同课章节目录
