第21—26章 阶段性综合练习题 (含解析) 2022-2—023学年人教版九年级数学
文档属性
| 名称 | 第21—26章 阶段性综合练习题 (含解析) 2022-2—023学年人教版九年级数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 653.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 00:00:00 | ||
图片预览




文档简介
2022-2023学年人教版九年级数学《第21—26章》阶段性综合练习题(附答案)
一、选择题(满分30分)
1.下列航天图标中,其图案是中心对称图形的是( )
A.B.C.D.
2.下列事件中,是随机事件的是( )
A.福州第四中学桔园洲中学第17届运动会没有在2022年进行
B.福州市2023年九上期末适应性练习没有如期进行
C.福州第四中学桔园洲中学2023年九上期末适应性练习如期进行
D.掷一枚硬币,正面朝上
3.将抛物线y=x2向上平移1个单位,就得到抛物线( )
A.y=x2+1 B.y=(x+1)2 C.y=x2﹣1 D.y=(x﹣1)2
4.反比例函数y=(k≠0)的图象经过点(﹣2,3),则该反比例函数图象在( )
A.第一,三象限 B.第二,四象限
C.第二,三象限 D.第一,二象限
5.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.150° B.75° C.60° D.15°
6.如图,直线l1∥l2∥l3,若AB=3,BC=4,则的值是( )
A. B. C. D.
7.边长为2的正六边形的外接圆半径是( )
A.1 B. C.2 D.
8.陈老师和与她搭班的李老师都十分热爱文学.某日,陈老师翻阅到一本古代数学著作—《增删算法统宗》,看到里面记载了这样一个问题:“今有门厅一座,不知门广高低,长午横进使归室,争奈门狭四尺,随即竖竿过去,亦长二尺无疑,两隅斜去恰方齐,请问三色各几?”.为了能够更通顺地读懂这个问题,陈老师找了李老师勾兑一二,最后得到了其可能的大意:“今有一房门,不知宽与高,长竿横着进门,门的宽度比竿小4尺进不了;将竿竖着进门,竿比门长2尺;将竿斜着穿过门的对角,恰好进门.试问门的宽、高和竿长各是多少?”根据翻译,她画出了这样一幅图,并设竿长AC为x尺,则下列方程中符合题意的是( )
A.(x﹣4)2+(x﹣2)2=x2 B.42+(x﹣2)2=x2
C.(x﹣4)2+(x﹣2)2=2x2 D.(x﹣4)2+22=x2
9.如图,AC是⊙O的直径,过⊙O外一点P作⊙O的两条切线,切点为A,B.若∠P=40°,则∠ACB的大小是( )
A.70° B.65° C.75° D.60°
10.已知非零实数a,b,c满足a+b+c=0,则下列不等式一定成立的是( )
A.a2﹣4bc>0 B.a2﹣4bc<0 C.c2﹣4ab≥0 D.b2﹣4ac≤0
二、填空题(满分18分)
11.方程(x﹣1)(x﹣2)=0的解为 .
12.往往高端的食材,只需要采用朴素的烹饪方式.当某房间里累积了足够多的丸子时,令人期待的午餐,也就飘香四溢了.在一个四宫格火锅里有倒下了两种锅底,一种是清汤锅底,一种是麻辣锅底.小伙伴们将100粒丸子随机投入四个宫格中,将其都装出后拿出房间,外面的小伙伴数了数有49粒是清汤味的,估计倒入红汤锅底的宫格数是 .
13.如图,A是反比例函数y=的图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B,C,则四边形OBAC的面积是 .
14.钟表的分针匀速旋转一周需要60分钟,分针在一节课45分钟的时间里旋转的角度是 .
15.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是 .
16.已知抛物线与直线交于A,B两点,C(﹣2,0),点P在线段AB上,且∠OPC=30°.若线段AB上满足条件的点P有两个,则a的取值范围是 .
三、解答题(满分72分)
17.解方程:x2+3x﹣2=0.
18.某学习小组为了测量校园内一棵小树AB的高度,用一根长为1米的竹竿CD作为测量工具.将竹竿垂直于地面放置,移动竹竿,使其影子的顶端,小树影子的顶端在水平地面上的同一点E处重合,且B,D,E三点共线.若测得BE长为4.5米,BD长为3米,求这棵小树AB的高度.
19.已知函数y=mx2+4x+2(m为常数)的图象与x轴只有一个公共点,求m的值.
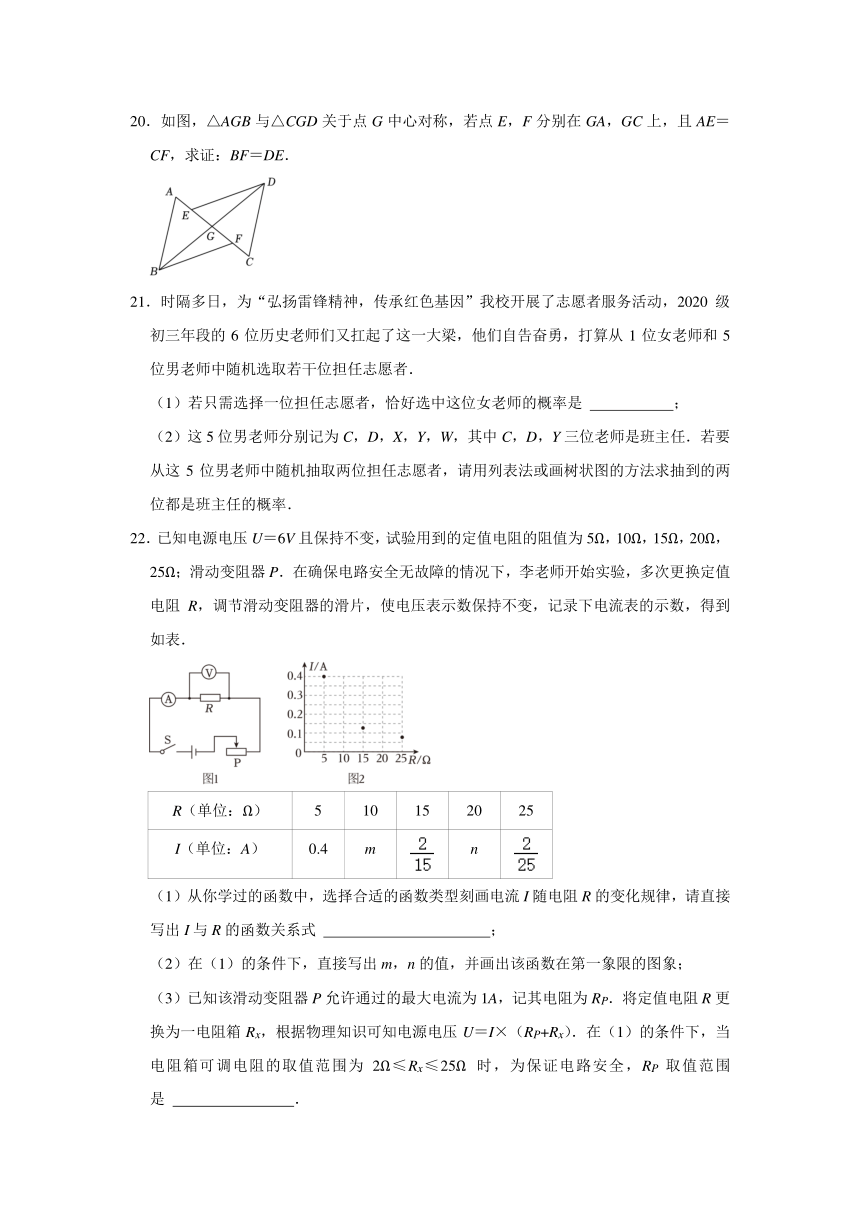
20.如图,△AGB与△CGD关于点G中心对称,若点E,F分别在GA,GC上,且AE=CF,求证:BF=DE.
21.时隔多日,为“弘扬雷锋精神,传承红色基因”我校开展了志愿者服务活动,2020级初三年段的6位历史老师们又扛起了这一大梁,他们自告奋勇,打算从1位女老师和5位男老师中随机选取若干位担任志愿者.
(1)若只需选择一位担任志愿者,恰好选中这位女老师的概率是 ;
(2)这5位男老师分别记为C,D,X,Y,W,其中C,D,Y三位老师是班主任.若要从这5位男老师中随机抽取两位担任志愿者,请用列表法或画树状图的方法求抽到的两位都是班主任的概率.
22.已知电源电压U=6V且保持不变,试验用到的定值电阻的阻值为5Ω,10Ω,15Ω,20Ω,25Ω;滑动变阻器P.在确保电路安全无故障的情况下,李老师开始实验,多次更换定值电阻R,调节滑动变阻器的滑片,使电压表示数保持不变,记录下电流表的示数,得到如表.
R(单位:Ω) 5 10 15 20 25
I(单位:A) 0.4 m n
(1)从你学过的函数中,选择合适的函数类型刻画电流I随电阻R的变化规律,请直接写出I与R的函数关系式 ;
(2)在(1)的条件下,直接写出m,n的值,并画出该函数在第一象限的图象;
(3)已知该滑动变阻器P允许通过的最大电流为1A,记其电阻为RP.将定值电阻R更换为一电阻箱Rx,根据物理知识可知电源电压U=I×(RP+Rx).在(1)的条件下,当电阻箱可调电阻的取值范围为2Ω≤Rx≤25Ω时,为保证电路安全,RP取值范围是 .
23.如图,AB是半圆O的直径,C为半圆O上一点.
(1)过点C作半圆O的切线交AB延长线于点D(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,过点C作AB的垂线,垂足为E,F为弧AC上一点(不与点A,C重合),连接FD,FE,若FD=2FE,求证:B是OD的中点.
24.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D.
(1)求证:△ABD∽△ACB;
(2)将△ABD绕点A顺时针旋转α(0°<α<180°)得到△AEF,其中E是点B的对应点.连接CE,取CE中点G,连接GB,GF.
①求证:GB=GF;
②连接BF,若AB=4,BC=3,求△BGF面积的最大值.
25.已知抛物线C:y=x2﹣4x+c,直线l:y=mx(m>0).当m=1时,直线l恰好经过抛物线C的顶点.
(1)求抛物线C的解析式;
(2)若直线l与抛物线C交于不同的两点A,B(点A在点B左侧),线段AB与直线l1:y=kx+b交于一点P(横坐标为xP).对于任意常数t(t>0),不论m取何值都有成立,求k的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,当存在m使得S△APQ=S△BPQ成立时,求点P横坐标xP的取值范围.
参考答案
一、选择题(满分30分)
1.解:选项A、C、D都不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形.
选项B能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形.
故选:B.
2.解:A、福州第四中学桔园洲中学第17届运动会没有在2022年进行,不是随机事件;
B、福州市2023年九上期末适应性练习没有如期进行,不是随机事件;
C、福州第四中学桔园洲中学2023年九上期末适应性练习如期进行,不是随机事件;
D、掷一枚硬币,正面朝上,是随机事件;
故选:D.
3.解:将抛物线y=x2向上平移1个单位得到的抛物线是y=x2+1.
故选:A.
4.解:反比例函数y=(k≠0)的图象经过点(﹣2,3),
则点(﹣2,3)一定在函数图象上,满足函数解析式,
代入解析式得到:k=﹣6,
因而反比例函数的解析式是y=,图象一定在第二,四象限.
故该反比例函数图象在第二,四象限.
故选:B.
5.解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选:B.
6.解:∵l1∥l2∥l3,
∴=,
且AC=AB+BC=7,
∴=,
故选:B.
7.解:如图,连接OB,OC,
∵六边形ABCDEF是正六边形,
∴∠BOC=360°÷6=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴边长为2的正六边形的外接圆半径为2,
故选:C.
8.解:设竿长AC为x尺,则BC=(x﹣4)尺,AB=(x﹣2)尺,
由勾股定理得AB2+BC2=AC2,
∴(x﹣4)2+(x﹣2)2=x2,
故选:A.
9.解:如图所示,连接OB,
∵PA、PB是⊙O的两条切线,
∴∠OAP=∠OBP=90°,
∵∠P=40°,
∴∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=140°,
∴,
故选:A.
10.解:∵非零实数a,b,c满足a+b+c=0,
∴a=﹣(b+c),
∴a2﹣4bc=[﹣(c+b)]2﹣4bc=(c﹣b)2≥0,
故选项A、B不正确,
同理,c2﹣4ab≥0,b2﹣4ac≥0,故选项C正确,D不正确,
故选:C.
二、填空题(满分18分)
11.解:∵(x﹣1)(x﹣2)=0,
∴x﹣1=0或x﹣2=0,
∴x1=1,x2=2.
故答案是x1=1,x2=2.
12.解:∵一共有100粒丸子,其中有49粒是清汤味的,
∴清汤味的概率为,
又∵一共有4个宫格,
∴清汤味的宫格数为2,
又∵在一个四宫格火锅里有倒下了两种锅底,一种是清汤锅底,一种是麻辣锅底,
∴红汤锅底的宫格数为1,
故答案为:1.
13.解:设A(m,n),
∵AC⊥y轴,AB⊥x轴,∠BOC=90°,
∴四边形OBAC是矩形,
∴OB=m,AB=n,
∴S四边形OBAC=OB AB=mn=k=6,
故答案为:6.
14.解:分针旋转角度=(度).
故答案为:270°.
15.解:过O作OC⊥AB于C,
∴AC=BC=AB=12,
在Rt△AOC中,由勾股定理得:OC==5,
故答案为:5.
16.解:联立,
解得:或,
令,
设直线与x轴交于点D,当y=0时,x=2,
∴D(2,0),
如图,连接AC,
∵,
则:,
∴△ACD为等边三角形,
∴∠CAD=∠CDA=∠ACD=60°,
∵AO⊥CD,
∴;
以O为圆心,OC的长为半径画圆,交直线AD于点P1,连接CP1,OP1,
则:OC=OP1=OD=2,
∴∠OCP1=∠OP1C,
∴△OP1D为等边三角形,
∴∠P1OD=60°,
又∵∠P1OD=∠OCP1+∠OP1C=2∠OP1C,
∴∠OP1C=30°;
过点P1作P1E⊥OD,则,
∴,
∴;
∴只要B点跟P1重合或在P1的右侧,即可满足线段AB上满足∠OPC=30°的点P有两个,即:A和P1两点,
∴,
∴;
故答案为:.
三、解答题(满分72分)
17.解:∵a=1,b=3,c=﹣2,
∴Δ=b2﹣4ac=32﹣4×1×(﹣2)=17,
∴x=,
∴x1=,x2=.
18.解:由题意得,CD⊥BE,AB⊥BE,DE=BE﹣BD=1.5米,
∴AB∥CD,
∴△EDC∽△EBA,
∴,即,
∴AB=3米,
∴这棵小树AB的高度为3米.
19.解:∵函数y=mx2+4x+2(m为常数)的图象与x轴只有一个公共点,
∴当m=0,y=0时,4x+2=0,
则,
∴此时函数y=mx2+4x+2的图象与x轴只有一个公共点,
当m≠0,y=0时,则方程mx2+4x+2=0只有一个实数根,
∴Δ=42﹣8m=0,
∴m=2;
综上所述,m=0或m=2.
20.证明:∵△AGB与△CGD关于点G中心对称,
∴BG=DG,AG=CG,
∵AE=CF,
∴AG﹣AE=CG﹣CF,
∴EG=FG,
又∵∠DGE=∠BGF,
∴△DGE≌△BGF(SAS),
∴BF=DE.
21.解:(1)从1位女老师和5位男老师中随机选取若干位担任志愿者,
若只需选择一位担任志愿者,恰好选中这位女老师的概率是;
故答案为:;
(2)画出树状图为:
共有20种等可能的结果数,其中抽取的两个老师恰好都是班主任的结果数为6,
所以抽取的两个老师恰好都是班主任的概率=.
22.解:(1)由题意得,电压表的度数为5×0.4=2V,
∴由欧姆定律得,
故答案为:;
(2)当R=10时,,
当R=20时,,
函数图象如下所示;
(3)由题意得U=I×(RP+Rx),
∴,
∵I≤1A,
∴RP+Rx≥6Ω,
∴RP≥4Ω;
又∵定值电阻的电压固定为2V,
∴电流的最小值为,
∴,
∴RP+Rx≤75Ω,
∴RP≤50Ω,
∴4Ω≤RP≤50Ω.
23.解:(1)如图,直线CD即为所求;
;
(2)证明:连接ON,CN,CF,
∵CD⊥OC,CE⊥OD,
∴∠DCO=∠DEC=90°,
∵∠CDO=∠EDC,
∴△DCO∽△DEC,
∴,即CD2=DE DO,
∵CD⊥OC,
∴∠DCN+∠NCO=90°,即∠DCN=90°﹣∠NCO,
∵ON=OC,
∴,
∴∠DCN=90°﹣(90°﹣∠CFN)=∠CFN,
∵∠CDN=∠FDC,
∴△CDN∽△FDC,
∴,即CD2=DN DF,
∴DE DO=DN DF,
∵∠DNO=∠DEF,
∴△DNO∽△DEF,
∴,
∵FD=2FE,ON=OB,
∴DO=2OB,
∴B是OD的中点.
24.(1)证明:∵BD⊥AC,
∴∠BDA=90°,
∴∠BDA=∠CBA,
又∵∠A=∠A,
∴△ABD∽△ACB;
(2)解:①如图所示,延长CB到M使得BM=BC,连接ME,BF,取AC中点H,连接BH,
由旋转的性质可得AB=AE,AD=AF,∠EAF=∠BAD,
∵CB=MB,∠ABC=∠ABM=90°,AB=AB,
∴△ABC≌△ABM(SAS),
∴AM=AC,∠BAC=∠BAM,
∴∠BAM=∠EAF,
∴∠BAM+∠BAE=∠EAF+∠BAE,即∠MAE=∠BAF,
∵△ABD∽△ACB,
∴,
∴,
∴△MAE∽△BAF,
∴,
∴,
∵B、G分别是CM,CE的中点,
∴BG为△CME的中位线,
∴ME=2BG,BG∥ME,
∴,
∴,
∵△MAE∽△BAF(可以看作把△MAE绕点A旋转∠BAC的大小,使两个三角形三条对应边都在一条直线上),
∴BF与ME的夹角为∠BAC,
∵BG∥ME,
∴BF与BG的夹角为∠BAC,即∠GBF=∠HAB,
∴△ABH∽△BFG,
∴,
∵∠ABC=90°,点H是AC的中点,
∴AH=BH,
∴,
∴BG=FG;
②如图所示,过点H作HN⊥AB于N,
∵△ABH∽△BFG,
∴,
∴当BF最大时,S△BGF最大,
∵AB=4,BC=3,
∴,
∵HN∥BC,
∴△ANH∽△ABC,
∴,即,
∴,
∴S△ABH=AB HN=×=3;
∵BF≤AB+AF,
∴当B、A、F三点共线时,BF最大,最大为AB+AF,
在Rt△ABC中,由勾股定理得,
∵△ABD∽△ACB,
∴,即,
∴,
∴,
∴,
∴.
25.解:(1)∵抛物线解析式为y=x2﹣4x+c=(x﹣2)2+c﹣4,
∴抛物线顶点坐标为(2,c﹣4),
∵当m=1时,直线l:y=mx(m>0)恰好经过抛物线C的顶点,
∴直线y=x经过点(2,c﹣4),
∴2=c﹣4,
∴c=6,
∴抛物线解析式为y=x2﹣4x+6;
(2)如图所示,过点A作AC⊥y轴于C,BE⊥y于E,PD⊥y于D,
∴AC∥PD∥BE,
∴△OAC∽△OPD,
∴,
同理可得,
∵,
∴,
∴,
∴,即=
联立得,
∴,
联立,得x2﹣(4+m)x+6=0,
∵AC、BE的长是方程x2﹣(4+m)x+6=0的两个根,
∴AC+BE=4+m,AC BE=6,
∴,
∴,
∴6t(m﹣k)=(m+4)b,
∴m(b﹣6t)=6tk+4b,
∵对于任意常数t(t>0),不论m取何值都有成立,
∴,
∴k=﹣4;
(3)∵S△APQ=S△BPQ,
∴AP=BP,即点P为AB的中点,
∴2PD=AC+BE,
∴,
∴,
∵方程x2﹣(4+m)x+6=0有两个不相等的实数根,
∴Δ=(4+m)2﹣4×6>0,
∴,
∴,
∴.
一、选择题(满分30分)
1.下列航天图标中,其图案是中心对称图形的是( )
A.B.C.D.
2.下列事件中,是随机事件的是( )
A.福州第四中学桔园洲中学第17届运动会没有在2022年进行
B.福州市2023年九上期末适应性练习没有如期进行
C.福州第四中学桔园洲中学2023年九上期末适应性练习如期进行
D.掷一枚硬币,正面朝上
3.将抛物线y=x2向上平移1个单位,就得到抛物线( )
A.y=x2+1 B.y=(x+1)2 C.y=x2﹣1 D.y=(x﹣1)2
4.反比例函数y=(k≠0)的图象经过点(﹣2,3),则该反比例函数图象在( )
A.第一,三象限 B.第二,四象限
C.第二,三象限 D.第一,二象限
5.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.150° B.75° C.60° D.15°
6.如图,直线l1∥l2∥l3,若AB=3,BC=4,则的值是( )
A. B. C. D.
7.边长为2的正六边形的外接圆半径是( )
A.1 B. C.2 D.
8.陈老师和与她搭班的李老师都十分热爱文学.某日,陈老师翻阅到一本古代数学著作—《增删算法统宗》,看到里面记载了这样一个问题:“今有门厅一座,不知门广高低,长午横进使归室,争奈门狭四尺,随即竖竿过去,亦长二尺无疑,两隅斜去恰方齐,请问三色各几?”.为了能够更通顺地读懂这个问题,陈老师找了李老师勾兑一二,最后得到了其可能的大意:“今有一房门,不知宽与高,长竿横着进门,门的宽度比竿小4尺进不了;将竿竖着进门,竿比门长2尺;将竿斜着穿过门的对角,恰好进门.试问门的宽、高和竿长各是多少?”根据翻译,她画出了这样一幅图,并设竿长AC为x尺,则下列方程中符合题意的是( )
A.(x﹣4)2+(x﹣2)2=x2 B.42+(x﹣2)2=x2
C.(x﹣4)2+(x﹣2)2=2x2 D.(x﹣4)2+22=x2
9.如图,AC是⊙O的直径,过⊙O外一点P作⊙O的两条切线,切点为A,B.若∠P=40°,则∠ACB的大小是( )
A.70° B.65° C.75° D.60°
10.已知非零实数a,b,c满足a+b+c=0,则下列不等式一定成立的是( )
A.a2﹣4bc>0 B.a2﹣4bc<0 C.c2﹣4ab≥0 D.b2﹣4ac≤0
二、填空题(满分18分)
11.方程(x﹣1)(x﹣2)=0的解为 .
12.往往高端的食材,只需要采用朴素的烹饪方式.当某房间里累积了足够多的丸子时,令人期待的午餐,也就飘香四溢了.在一个四宫格火锅里有倒下了两种锅底,一种是清汤锅底,一种是麻辣锅底.小伙伴们将100粒丸子随机投入四个宫格中,将其都装出后拿出房间,外面的小伙伴数了数有49粒是清汤味的,估计倒入红汤锅底的宫格数是 .
13.如图,A是反比例函数y=的图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B,C,则四边形OBAC的面积是 .
14.钟表的分针匀速旋转一周需要60分钟,分针在一节课45分钟的时间里旋转的角度是 .
15.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是 .
16.已知抛物线与直线交于A,B两点,C(﹣2,0),点P在线段AB上,且∠OPC=30°.若线段AB上满足条件的点P有两个,则a的取值范围是 .
三、解答题(满分72分)
17.解方程:x2+3x﹣2=0.
18.某学习小组为了测量校园内一棵小树AB的高度,用一根长为1米的竹竿CD作为测量工具.将竹竿垂直于地面放置,移动竹竿,使其影子的顶端,小树影子的顶端在水平地面上的同一点E处重合,且B,D,E三点共线.若测得BE长为4.5米,BD长为3米,求这棵小树AB的高度.
19.已知函数y=mx2+4x+2(m为常数)的图象与x轴只有一个公共点,求m的值.
20.如图,△AGB与△CGD关于点G中心对称,若点E,F分别在GA,GC上,且AE=CF,求证:BF=DE.
21.时隔多日,为“弘扬雷锋精神,传承红色基因”我校开展了志愿者服务活动,2020级初三年段的6位历史老师们又扛起了这一大梁,他们自告奋勇,打算从1位女老师和5位男老师中随机选取若干位担任志愿者.
(1)若只需选择一位担任志愿者,恰好选中这位女老师的概率是 ;
(2)这5位男老师分别记为C,D,X,Y,W,其中C,D,Y三位老师是班主任.若要从这5位男老师中随机抽取两位担任志愿者,请用列表法或画树状图的方法求抽到的两位都是班主任的概率.
22.已知电源电压U=6V且保持不变,试验用到的定值电阻的阻值为5Ω,10Ω,15Ω,20Ω,25Ω;滑动变阻器P.在确保电路安全无故障的情况下,李老师开始实验,多次更换定值电阻R,调节滑动变阻器的滑片,使电压表示数保持不变,记录下电流表的示数,得到如表.
R(单位:Ω) 5 10 15 20 25
I(单位:A) 0.4 m n
(1)从你学过的函数中,选择合适的函数类型刻画电流I随电阻R的变化规律,请直接写出I与R的函数关系式 ;
(2)在(1)的条件下,直接写出m,n的值,并画出该函数在第一象限的图象;
(3)已知该滑动变阻器P允许通过的最大电流为1A,记其电阻为RP.将定值电阻R更换为一电阻箱Rx,根据物理知识可知电源电压U=I×(RP+Rx).在(1)的条件下,当电阻箱可调电阻的取值范围为2Ω≤Rx≤25Ω时,为保证电路安全,RP取值范围是 .
23.如图,AB是半圆O的直径,C为半圆O上一点.
(1)过点C作半圆O的切线交AB延长线于点D(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,过点C作AB的垂线,垂足为E,F为弧AC上一点(不与点A,C重合),连接FD,FE,若FD=2FE,求证:B是OD的中点.
24.如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D.
(1)求证:△ABD∽△ACB;
(2)将△ABD绕点A顺时针旋转α(0°<α<180°)得到△AEF,其中E是点B的对应点.连接CE,取CE中点G,连接GB,GF.
①求证:GB=GF;
②连接BF,若AB=4,BC=3,求△BGF面积的最大值.
25.已知抛物线C:y=x2﹣4x+c,直线l:y=mx(m>0).当m=1时,直线l恰好经过抛物线C的顶点.
(1)求抛物线C的解析式;
(2)若直线l与抛物线C交于不同的两点A,B(点A在点B左侧),线段AB与直线l1:y=kx+b交于一点P(横坐标为xP).对于任意常数t(t>0),不论m取何值都有成立,求k的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,当存在m使得S△APQ=S△BPQ成立时,求点P横坐标xP的取值范围.
参考答案
一、选择题(满分30分)
1.解:选项A、C、D都不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形.
选项B能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形.
故选:B.
2.解:A、福州第四中学桔园洲中学第17届运动会没有在2022年进行,不是随机事件;
B、福州市2023年九上期末适应性练习没有如期进行,不是随机事件;
C、福州第四中学桔园洲中学2023年九上期末适应性练习如期进行,不是随机事件;
D、掷一枚硬币,正面朝上,是随机事件;
故选:D.
3.解:将抛物线y=x2向上平移1个单位得到的抛物线是y=x2+1.
故选:A.
4.解:反比例函数y=(k≠0)的图象经过点(﹣2,3),
则点(﹣2,3)一定在函数图象上,满足函数解析式,
代入解析式得到:k=﹣6,
因而反比例函数的解析式是y=,图象一定在第二,四象限.
故该反比例函数图象在第二,四象限.
故选:B.
5.解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选:B.
6.解:∵l1∥l2∥l3,
∴=,
且AC=AB+BC=7,
∴=,
故选:B.
7.解:如图,连接OB,OC,
∵六边形ABCDEF是正六边形,
∴∠BOC=360°÷6=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴边长为2的正六边形的外接圆半径为2,
故选:C.
8.解:设竿长AC为x尺,则BC=(x﹣4)尺,AB=(x﹣2)尺,
由勾股定理得AB2+BC2=AC2,
∴(x﹣4)2+(x﹣2)2=x2,
故选:A.
9.解:如图所示,连接OB,
∵PA、PB是⊙O的两条切线,
∴∠OAP=∠OBP=90°,
∵∠P=40°,
∴∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=140°,
∴,
故选:A.
10.解:∵非零实数a,b,c满足a+b+c=0,
∴a=﹣(b+c),
∴a2﹣4bc=[﹣(c+b)]2﹣4bc=(c﹣b)2≥0,
故选项A、B不正确,
同理,c2﹣4ab≥0,b2﹣4ac≥0,故选项C正确,D不正确,
故选:C.
二、填空题(满分18分)
11.解:∵(x﹣1)(x﹣2)=0,
∴x﹣1=0或x﹣2=0,
∴x1=1,x2=2.
故答案是x1=1,x2=2.
12.解:∵一共有100粒丸子,其中有49粒是清汤味的,
∴清汤味的概率为,
又∵一共有4个宫格,
∴清汤味的宫格数为2,
又∵在一个四宫格火锅里有倒下了两种锅底,一种是清汤锅底,一种是麻辣锅底,
∴红汤锅底的宫格数为1,
故答案为:1.
13.解:设A(m,n),
∵AC⊥y轴,AB⊥x轴,∠BOC=90°,
∴四边形OBAC是矩形,
∴OB=m,AB=n,
∴S四边形OBAC=OB AB=mn=k=6,
故答案为:6.
14.解:分针旋转角度=(度).
故答案为:270°.
15.解:过O作OC⊥AB于C,
∴AC=BC=AB=12,
在Rt△AOC中,由勾股定理得:OC==5,
故答案为:5.
16.解:联立,
解得:或,
令,
设直线与x轴交于点D,当y=0时,x=2,
∴D(2,0),
如图,连接AC,
∵,
则:,
∴△ACD为等边三角形,
∴∠CAD=∠CDA=∠ACD=60°,
∵AO⊥CD,
∴;
以O为圆心,OC的长为半径画圆,交直线AD于点P1,连接CP1,OP1,
则:OC=OP1=OD=2,
∴∠OCP1=∠OP1C,
∴△OP1D为等边三角形,
∴∠P1OD=60°,
又∵∠P1OD=∠OCP1+∠OP1C=2∠OP1C,
∴∠OP1C=30°;
过点P1作P1E⊥OD,则,
∴,
∴;
∴只要B点跟P1重合或在P1的右侧,即可满足线段AB上满足∠OPC=30°的点P有两个,即:A和P1两点,
∴,
∴;
故答案为:.
三、解答题(满分72分)
17.解:∵a=1,b=3,c=﹣2,
∴Δ=b2﹣4ac=32﹣4×1×(﹣2)=17,
∴x=,
∴x1=,x2=.
18.解:由题意得,CD⊥BE,AB⊥BE,DE=BE﹣BD=1.5米,
∴AB∥CD,
∴△EDC∽△EBA,
∴,即,
∴AB=3米,
∴这棵小树AB的高度为3米.
19.解:∵函数y=mx2+4x+2(m为常数)的图象与x轴只有一个公共点,
∴当m=0,y=0时,4x+2=0,
则,
∴此时函数y=mx2+4x+2的图象与x轴只有一个公共点,
当m≠0,y=0时,则方程mx2+4x+2=0只有一个实数根,
∴Δ=42﹣8m=0,
∴m=2;
综上所述,m=0或m=2.
20.证明:∵△AGB与△CGD关于点G中心对称,
∴BG=DG,AG=CG,
∵AE=CF,
∴AG﹣AE=CG﹣CF,
∴EG=FG,
又∵∠DGE=∠BGF,
∴△DGE≌△BGF(SAS),
∴BF=DE.
21.解:(1)从1位女老师和5位男老师中随机选取若干位担任志愿者,
若只需选择一位担任志愿者,恰好选中这位女老师的概率是;
故答案为:;
(2)画出树状图为:
共有20种等可能的结果数,其中抽取的两个老师恰好都是班主任的结果数为6,
所以抽取的两个老师恰好都是班主任的概率=.
22.解:(1)由题意得,电压表的度数为5×0.4=2V,
∴由欧姆定律得,
故答案为:;
(2)当R=10时,,
当R=20时,,
函数图象如下所示;
(3)由题意得U=I×(RP+Rx),
∴,
∵I≤1A,
∴RP+Rx≥6Ω,
∴RP≥4Ω;
又∵定值电阻的电压固定为2V,
∴电流的最小值为,
∴,
∴RP+Rx≤75Ω,
∴RP≤50Ω,
∴4Ω≤RP≤50Ω.
23.解:(1)如图,直线CD即为所求;
;
(2)证明:连接ON,CN,CF,
∵CD⊥OC,CE⊥OD,
∴∠DCO=∠DEC=90°,
∵∠CDO=∠EDC,
∴△DCO∽△DEC,
∴,即CD2=DE DO,
∵CD⊥OC,
∴∠DCN+∠NCO=90°,即∠DCN=90°﹣∠NCO,
∵ON=OC,
∴,
∴∠DCN=90°﹣(90°﹣∠CFN)=∠CFN,
∵∠CDN=∠FDC,
∴△CDN∽△FDC,
∴,即CD2=DN DF,
∴DE DO=DN DF,
∵∠DNO=∠DEF,
∴△DNO∽△DEF,
∴,
∵FD=2FE,ON=OB,
∴DO=2OB,
∴B是OD的中点.
24.(1)证明:∵BD⊥AC,
∴∠BDA=90°,
∴∠BDA=∠CBA,
又∵∠A=∠A,
∴△ABD∽△ACB;
(2)解:①如图所示,延长CB到M使得BM=BC,连接ME,BF,取AC中点H,连接BH,
由旋转的性质可得AB=AE,AD=AF,∠EAF=∠BAD,
∵CB=MB,∠ABC=∠ABM=90°,AB=AB,
∴△ABC≌△ABM(SAS),
∴AM=AC,∠BAC=∠BAM,
∴∠BAM=∠EAF,
∴∠BAM+∠BAE=∠EAF+∠BAE,即∠MAE=∠BAF,
∵△ABD∽△ACB,
∴,
∴,
∴△MAE∽△BAF,
∴,
∴,
∵B、G分别是CM,CE的中点,
∴BG为△CME的中位线,
∴ME=2BG,BG∥ME,
∴,
∴,
∵△MAE∽△BAF(可以看作把△MAE绕点A旋转∠BAC的大小,使两个三角形三条对应边都在一条直线上),
∴BF与ME的夹角为∠BAC,
∵BG∥ME,
∴BF与BG的夹角为∠BAC,即∠GBF=∠HAB,
∴△ABH∽△BFG,
∴,
∵∠ABC=90°,点H是AC的中点,
∴AH=BH,
∴,
∴BG=FG;
②如图所示,过点H作HN⊥AB于N,
∵△ABH∽△BFG,
∴,
∴当BF最大时,S△BGF最大,
∵AB=4,BC=3,
∴,
∵HN∥BC,
∴△ANH∽△ABC,
∴,即,
∴,
∴S△ABH=AB HN=×=3;
∵BF≤AB+AF,
∴当B、A、F三点共线时,BF最大,最大为AB+AF,
在Rt△ABC中,由勾股定理得,
∵△ABD∽△ACB,
∴,即,
∴,
∴,
∴,
∴.
25.解:(1)∵抛物线解析式为y=x2﹣4x+c=(x﹣2)2+c﹣4,
∴抛物线顶点坐标为(2,c﹣4),
∵当m=1时,直线l:y=mx(m>0)恰好经过抛物线C的顶点,
∴直线y=x经过点(2,c﹣4),
∴2=c﹣4,
∴c=6,
∴抛物线解析式为y=x2﹣4x+6;
(2)如图所示,过点A作AC⊥y轴于C,BE⊥y于E,PD⊥y于D,
∴AC∥PD∥BE,
∴△OAC∽△OPD,
∴,
同理可得,
∵,
∴,
∴,
∴,即=
联立得,
∴,
联立,得x2﹣(4+m)x+6=0,
∵AC、BE的长是方程x2﹣(4+m)x+6=0的两个根,
∴AC+BE=4+m,AC BE=6,
∴,
∴,
∴6t(m﹣k)=(m+4)b,
∴m(b﹣6t)=6tk+4b,
∵对于任意常数t(t>0),不论m取何值都有成立,
∴,
∴k=﹣4;
(3)∵S△APQ=S△BPQ,
∴AP=BP,即点P为AB的中点,
∴2PD=AC+BE,
∴,
∴,
∵方程x2﹣(4+m)x+6=0有两个不相等的实数根,
∴Δ=(4+m)2﹣4×6>0,
∴,
∴,
∴.
同课章节目录
