江苏省盐城市大丰区 2023—2024学年上学期八年级数学第11周提优练习(含答案)
文档属性
| 名称 | 江苏省盐城市大丰区 2023—2024学年上学期八年级数学第11周提优练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 742.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 09:05:34 | ||
图片预览


文档简介
2023~2024学年度第一学期
八年级数学第11周提优练习
(时间:80分钟 分值:100分)
一、填空题(共5小题,每题4分,共20分)
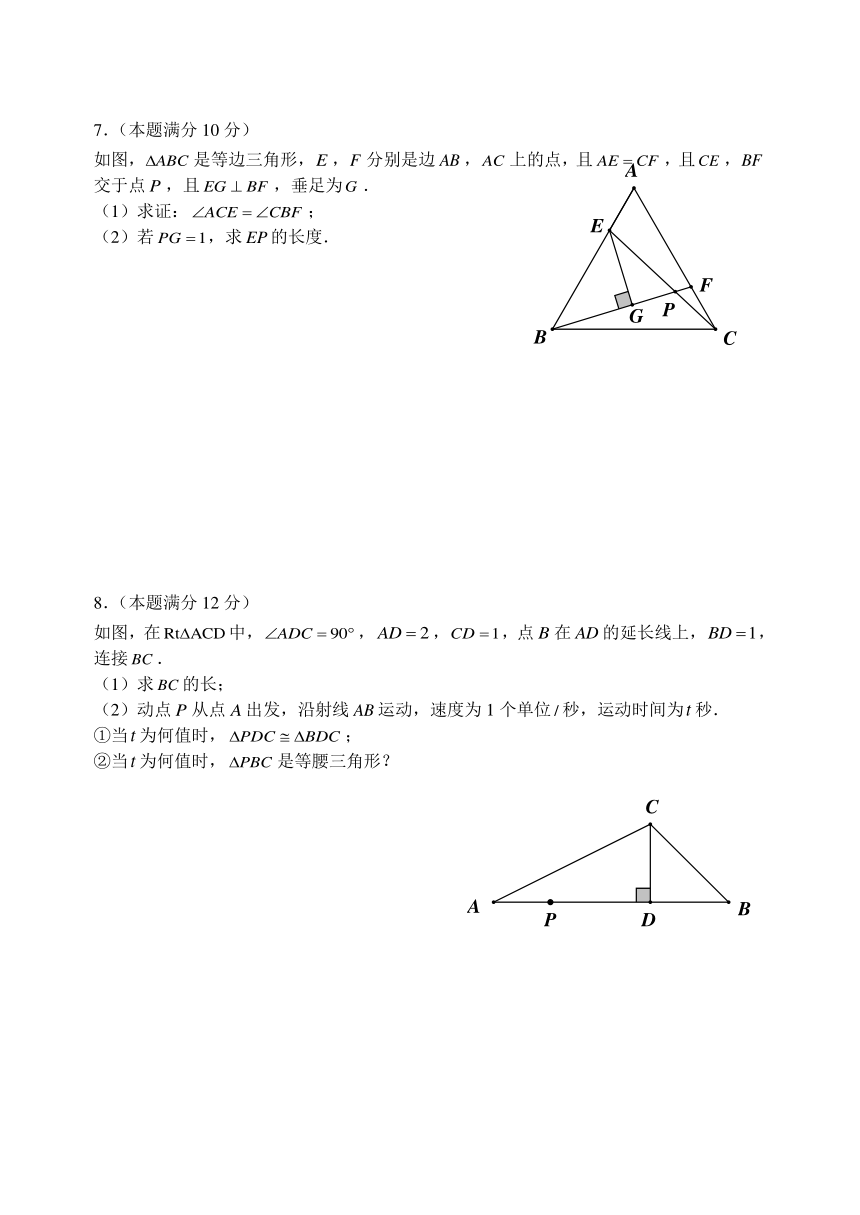
1.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为 ▲ .
2.如图,在中,,,,是的平分线.若,分别是和上的动点,则的最小值是 ▲ .
第1题 第2题 第3题
3.如图,在中,,,,线段,连接,绕点顺时针旋转一周,在运动过程中,当、、三点在同一条直线上时,则的长为 ▲ .
4.在正方形网格中,、、、、均为格点,则 ▲ .
5.如图,在中,,,的平分线与的垂直平分线相交于点,点沿折叠后与重合,则 ▲ .
(
A
B
C
E
D
)
二、解答题(共7小题,共80分)
6.(本题满分10分)
如图,一张长方形纸片中,,.将矩形纸片沿过点的直线折叠,使点落到边上的点处,折痕交于点.
(1)试用尺规在图中作出点和折痕(不写作法,保留作图痕迹);
(2)若,,求的长.
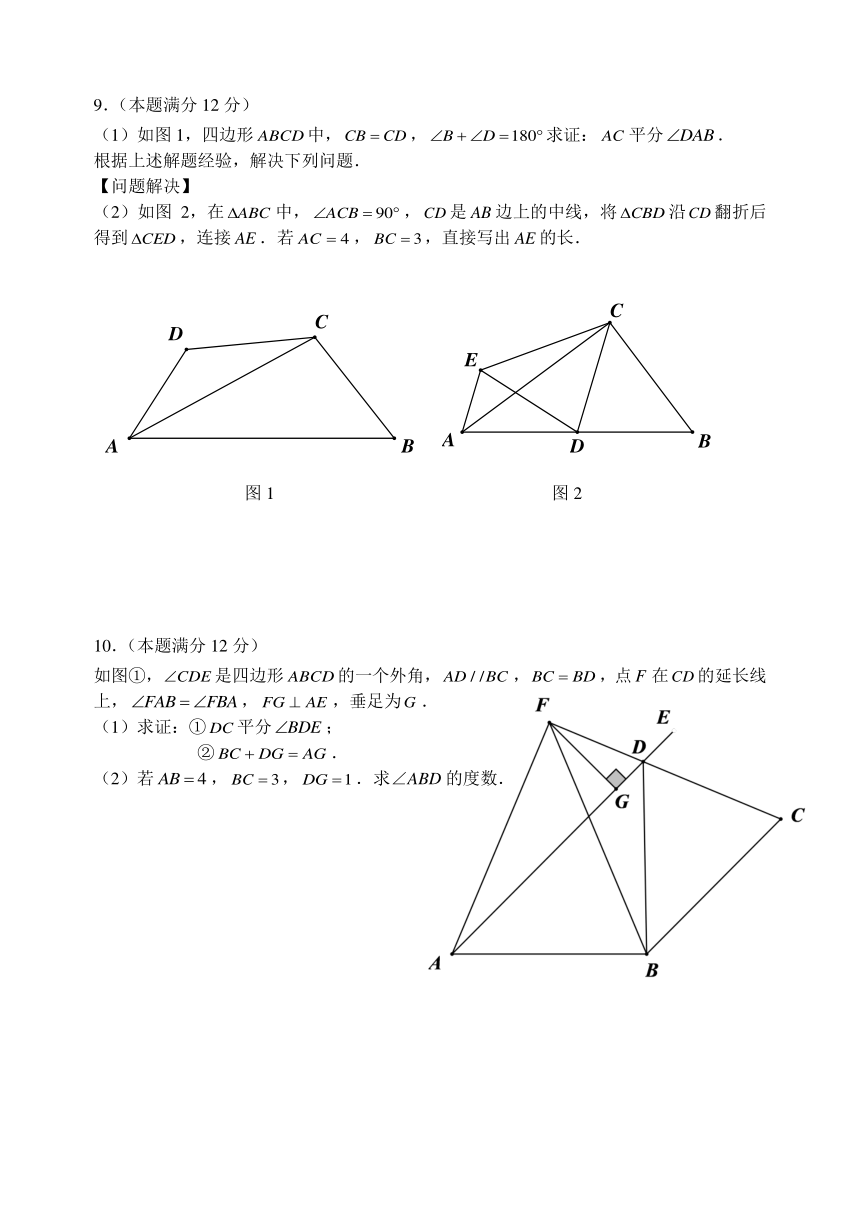
7.(本题满分10分)
如图,是等边三角形,,分别是边,上的点,且,且,交于点,且,垂足为.
(1)求证:;
(2)若,求的长度.
8.(本题满分12分)
如图,在中,,,,点在的延长线上,,连接.
(1)求的长;
(2)动点从点出发,沿射线运动,速度为1个单位秒,运动时间为秒.
①当为何值时,;
②当为何值时,是等腰三角形?
9.(本题满分12分)
(1)如图1,四边形中,,求证:平分.
根据上述解题经验,解决下列问题.
【问题解决】
(2)如图2,在中,,是边上的中线,将沿翻折后得到,连接.若,,直接写出的长.
图1 图2
10.(本题满分12分)
如图①,是四边形的一个外角,,,点在的延长线上,,,垂足为.
(1)求证:①平分;
②.
(2)若,,.求∠ABD的度数.
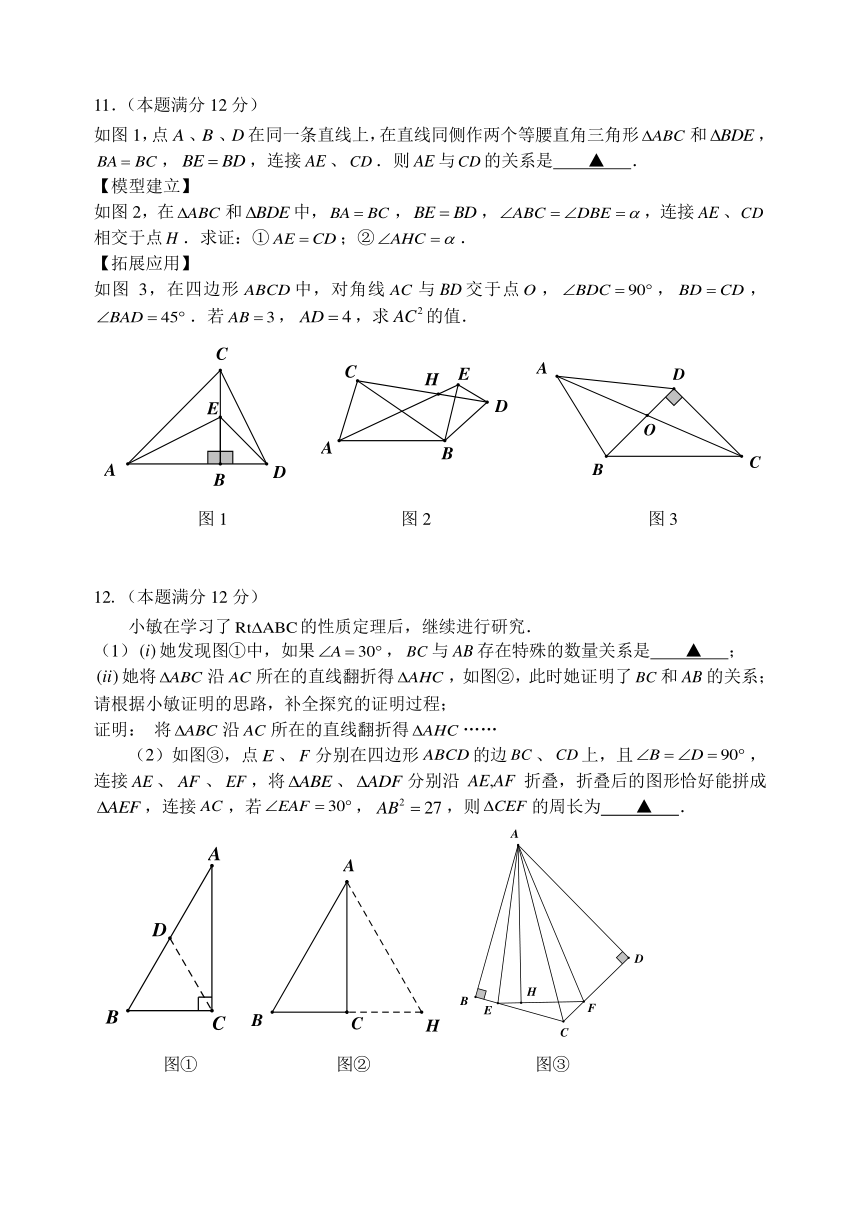
11.(本题满分12分)
如图1,点、、在同一条直线上,在直线同侧作两个等腰直角三角形和,,,连接、.则与的关系是 ▲ .
【模型建立】
如图2,在和中,,,,连接、相交于点.求证:①;②.
【拓展应用】
如图3,在四边形中,对角线与交于点,,,.若,,求的值.
图1 图2 图3
12.(本题满分12分)
小敏在学习了的性质定理后,继续进行研究.
(1)她发现图①中,如果,与存在特殊的数量关系是 ▲ ;
她将沿所在的直线翻折得,如图②,此时她证明了和的关系;请根据小敏证明的思路,补全探究的证明过程;
证明: 将沿所在的直线翻折得……
(2)如图③,点、分别在四边形的边、上,且,连接、、,将、分别沿AE,AF折叠,折叠后的图形恰好能拼成,连接,若,,则的周长为 ▲ .
图① 图② 图③
参考答案与评分标准
一、填空题(共5小题,每题4分,共20分)
1. 1 2. 3.14或2 4.45 5.20
二、解答题(共7小题,共70分)
6.(本题满分10分)
解:(1)如图,点,直线即为所求.
(2)四边形是矩形,
,
,,
,
,
设,
在中,,
,
,
.
7.(本题满分10分)
证明:(1)是等边三角形,
,,,
在与中,
,
,
;
(2)解:由(1)知,
又,
,
,
,即,
,
在中,,
,
.
8.(本题满分12分)
解:(1),,,
;
(2)①,
,即,解得;
或点与重合,此时,
综上所述,满足条件的的值为1或3;
②当时,,
,
,
当时,点与点重合时,
,
;
当时,
,
BP=,解得,
故当或2或时,为等腰三角形.
9.(本题满分12分)
证明:(1)如图,过点作于,过点作,交的延长线于,
,,
,
又,,
,
在和中,
,
,
,
又,,
平分;
(2)如图2,过点作于,过点作,交的延长线于,连接,
,,,
,
,
,
,
,
,
将沿翻折后得到,
,,,
,是边上的中线,
,
,,
,
,
又,,
,
,,
又,
,
,
.
10.(本题满分12分)
(1)证明:①,
,
,
,
,
平分;
②如图,过点作,交的延长线于点,
,,,
,,,
,,
在与中,
,
,
,
,
,
,
在与中,
,
,
,
;
(2)解:①若,,,则,
,
,
,
是直角三角形,,
11.(本题满分12分)
解:【引例】结论:,.
【模型建立】如图2中,设交于点.
,
,
,,
,
,
,,,
,即.
【拓展应用】如图3中,作,截取,连接,.则,,
,
,
,,
,
,
,
,
在中,,
在中,,
,,
,,
.
12.(本题满分12分)
解:(1),
将沿所在的直线翻折得,
,
,,,
,且,
是等边三角形,
,
;
(2)6.
八年级数学第11周提优练习
(时间:80分钟 分值:100分)
一、填空题(共5小题,每题4分,共20分)
1.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为 ▲ .
2.如图,在中,,,,是的平分线.若,分别是和上的动点,则的最小值是 ▲ .
第1题 第2题 第3题
3.如图,在中,,,,线段,连接,绕点顺时针旋转一周,在运动过程中,当、、三点在同一条直线上时,则的长为 ▲ .
4.在正方形网格中,、、、、均为格点,则 ▲ .
5.如图,在中,,,的平分线与的垂直平分线相交于点,点沿折叠后与重合,则 ▲ .
(
A
B
C
E
D
)
二、解答题(共7小题,共80分)
6.(本题满分10分)
如图,一张长方形纸片中,,.将矩形纸片沿过点的直线折叠,使点落到边上的点处,折痕交于点.
(1)试用尺规在图中作出点和折痕(不写作法,保留作图痕迹);
(2)若,,求的长.
7.(本题满分10分)
如图,是等边三角形,,分别是边,上的点,且,且,交于点,且,垂足为.
(1)求证:;
(2)若,求的长度.
8.(本题满分12分)
如图,在中,,,,点在的延长线上,,连接.
(1)求的长;
(2)动点从点出发,沿射线运动,速度为1个单位秒,运动时间为秒.
①当为何值时,;
②当为何值时,是等腰三角形?
9.(本题满分12分)
(1)如图1,四边形中,,求证:平分.
根据上述解题经验,解决下列问题.
【问题解决】
(2)如图2,在中,,是边上的中线,将沿翻折后得到,连接.若,,直接写出的长.
图1 图2
10.(本题满分12分)
如图①,是四边形的一个外角,,,点在的延长线上,,,垂足为.
(1)求证:①平分;
②.
(2)若,,.求∠ABD的度数.
11.(本题满分12分)
如图1,点、、在同一条直线上,在直线同侧作两个等腰直角三角形和,,,连接、.则与的关系是 ▲ .
【模型建立】
如图2,在和中,,,,连接、相交于点.求证:①;②.
【拓展应用】
如图3,在四边形中,对角线与交于点,,,.若,,求的值.
图1 图2 图3
12.(本题满分12分)
小敏在学习了的性质定理后,继续进行研究.
(1)她发现图①中,如果,与存在特殊的数量关系是 ▲ ;
她将沿所在的直线翻折得,如图②,此时她证明了和的关系;请根据小敏证明的思路,补全探究的证明过程;
证明: 将沿所在的直线翻折得……
(2)如图③,点、分别在四边形的边、上,且,连接、、,将、分别沿AE,AF折叠,折叠后的图形恰好能拼成,连接,若,,则的周长为 ▲ .
图① 图② 图③
参考答案与评分标准
一、填空题(共5小题,每题4分,共20分)
1. 1 2. 3.14或2 4.45 5.20
二、解答题(共7小题,共70分)
6.(本题满分10分)
解:(1)如图,点,直线即为所求.
(2)四边形是矩形,
,
,,
,
,
设,
在中,,
,
,
.
7.(本题满分10分)
证明:(1)是等边三角形,
,,,
在与中,
,
,
;
(2)解:由(1)知,
又,
,
,
,即,
,
在中,,
,
.
8.(本题满分12分)
解:(1),,,
;
(2)①,
,即,解得;
或点与重合,此时,
综上所述,满足条件的的值为1或3;
②当时,,
,
,
当时,点与点重合时,
,
;
当时,
,
BP=,解得,
故当或2或时,为等腰三角形.
9.(本题满分12分)
证明:(1)如图,过点作于,过点作,交的延长线于,
,,
,
又,,
,
在和中,
,
,
,
又,,
平分;
(2)如图2,过点作于,过点作,交的延长线于,连接,
,,,
,
,
,
,
,
,
将沿翻折后得到,
,,,
,是边上的中线,
,
,,
,
,
又,,
,
,,
又,
,
,
.
10.(本题满分12分)
(1)证明:①,
,
,
,
,
平分;
②如图,过点作,交的延长线于点,
,,,
,,,
,,
在与中,
,
,
,
,
,
,
在与中,
,
,
,
;
(2)解:①若,,,则,
,
,
,
是直角三角形,,
11.(本题满分12分)
解:【引例】结论:,.
【模型建立】如图2中,设交于点.
,
,
,,
,
,
,,,
,即.
【拓展应用】如图3中,作,截取,连接,.则,,
,
,
,,
,
,
,
,
在中,,
在中,,
,,
,,
.
12.(本题满分12分)
解:(1),
将沿所在的直线翻折得,
,
,,,
,且,
是等边三角形,
,
;
(2)6.
