河南省固始县2023-2024学年高二上学期期中考试数学试题(含解析)
文档属性
| 名称 | 河南省固始县2023-2024学年高二上学期期中考试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 927.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-17 16:00:07 | ||
图片预览




文档简介
绝密★启用前
固始县2023-2024学年高二上学期期中考试
数学试题
(考试用时120分钟 试卷满分150分)
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应科目的答案标号涂黑。如需改动,橡皮擦干净后,涂上其他答案标号。
3.回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将答题卡交回。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若直线:与:平行,则两直线之间的距离为( )
A. B.1 C. D.2
2.在x,y轴上的截距分别为4,的直线l被圆C:截得的弦长为( )
A.3 B.6 C. D.
3.已知圆心为的圆与直线相切,则该圆的标准方程是( )
A. B.
C. D.
4.已知,,,若平面ABC的一个法向量为,则( )
A. B. C. D.
5.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
A. B. C. D.
6.抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件A,“第二次向上的点数是奇数”为事件B,“两次向上的点数之和能被3整除”为事件C,则下列说法正确的是( )
A.事件A与事件B互为对立事件 B.
C. D.事件B与事件C相互不独立
7.如图,在四面体OABC中,,,.点M在OA上,且,N为BC中点,则等于( )
A. B. C. D.
8.已知直三棱柱,在中,,,,则异面直线与所成角为( )
A. B. C. D.
二、多项选择题(本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得3分,有选错的得0分)
9.判断下列结论正确的是( )
A.空间中任意两个非零向量,共面.
B.在三个向量的数量积运算中.
C.对于非零向量,由数量积,则.
D.若A,B,C,D是空间任意四点,则有.
10.已知直线l过点,且直线l在坐标轴上的截距的绝对值相等,则直线l的方程为( )
A. B. C. D.
11.若圆上恒有4个点到直线的距离为1,则实数r的可能取值是( )
A. B. C.3 D.
12.不透明的袋子中装有6个大小质地相同的小球,分别标有数字1,2,3,4,5,6,从中有放回的随机抽取两次,每次取一个球.A表示事件“第二次取出的球上标有的数字大于等于3”,B表示事件“两次取出的球上标有的数字之和为5,则( )
A. B. C. D.事件A与B相互独立
第Ⅱ卷(非选择题,共90分)
三、填空题:(本大题共4小题,每小题5分,共20分.把答案填写在题中横线上)
13.已知两点,,点P满足,则点P的轨迹方程为 .
14.现有3张分别标有1、3、5的卡片,采取有放回的方式从中依次随机取出2张卡片,则抽到的2张卡片的数字之和不小于8的概率是 .
15.如图,在正四面体P-ABC中,M,N分别为PA,BC的中点,D是线段MN上一点,且,若,则的值为 .
16.已知直线l:与曲线有两个交点,则k的取值范围为 .
四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.已知△ABC三个顶点的坐标分别为,,.求:
(1)过点且与直线BC平行的直线方程.
(2)△ABC中,AC边上的高所在直线的方程.
18.药品监督局检测某种产品的两个质量指标x,y,用综合指标核定该产品的等级.若,则核定该产品为一等品.现从一批该产品中随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
质量指标
产品编号
质量指标
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件B为“在抽取的2件产品中,每件产品的综合指标均满足”,求事件B的概率.
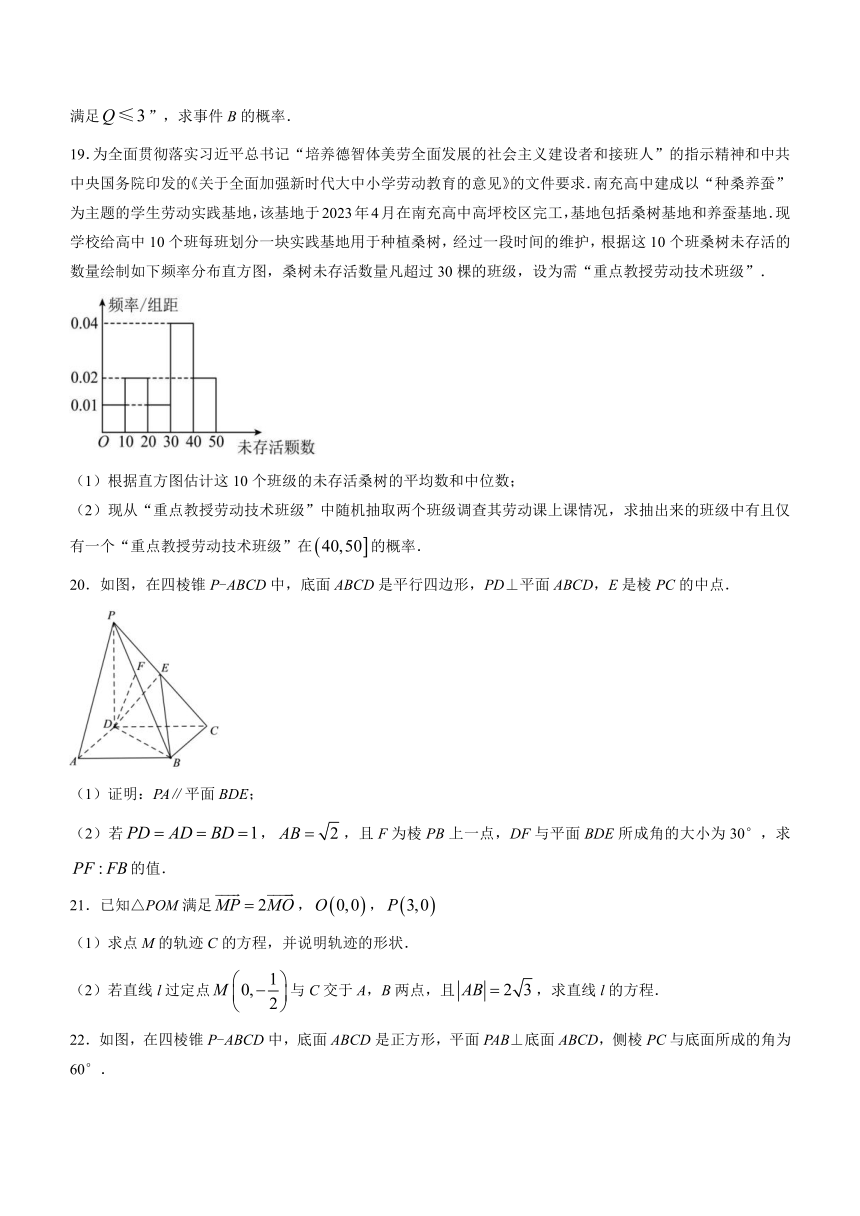
19.为全面贯彻落实习近平总书记“培养德智体美劳全面发展的社会主义建设者和接班人”的指示精神和中共中央国务院印发的《关于全面加强新时代大中小学劳动教育的意见》的文件要求.南充高中建成以“种桑养蚕”为主题的学生劳动实践基地,该基地于2023年4月在南充高中高坪校区完工,基地包括桑树基地和养蚕基地.现学校给高中10个班每班划分一块实践基地用于种植桑树,经过一段时间的维护,根据这10个班桑树未存活的数量绘制如下频率分布直方图,桑树未存活数量凡超过30棵的班级,设为需“重点教授劳动技术班级”.
(1)根据直方图估计这10个班级的未存活桑树的平均数和中位数;
(2)现从“重点教授劳动技术班级”中随机抽取两个班级调查其劳动课上课情况,求抽出来的班级中有且仅有一个“重点教授劳动技术班级”在的概率.
20.如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥平面ABCD,E是棱PC的中点.
(1)证明:PA∥平面BDE;
(2)若,,且F为棱PB上一点,DF与平面BDE所成角的大小为30°,求的值.
21.已知△POM满足,,
(1)求点M的轨迹C的方程,并说明轨迹的形状.
(2)若直线l过定点与C交于A,B两点,且,求直线l的方程.
22.如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PAB⊥底面ABCD,侧棱PC与底面所成的角为60°.
(1)证明:平面PAB⊥平面PAD;
(2)若平面PBD⊥平面PAC,求二面角B-PC-D的正弦值.
参考答案:
1.C
【分析】根据两直线平行可得,再由平行线间的距离公式即可求得结果.
【详解】依题意,由两直线平行可知,解得,
所以两直线分别为,,
可得两直线之间的距离为,
故选:C.
2.B
【分析】根据题意,求得直线l的方程为,结合圆的弦长公式,即可求解.
【详解】由题意得,直线l的方程为,即,
又由C:,可化为,
可得圆C的圆心为,半径为,则圆心到直线l的距离,
所以直线l被圆C截得的弦长为.
故选:B.
3.A
【分析】由圆心到切线的距离等于半径,求出圆的半径,即可得到本题答案.
【详解】因为圆心为的圆与直线相切,所以圆心到直线的距离等于半径,
即,
所以该圆的标准方程是.
故选:A
4.C
【分析】利用法向量和平面内直线的方向向量之间的关系求解即可.
【详解】由,,得:
,,
面ABC的一个法向量为,
所以,,
即,,
解得,,
所以,
故选:C.
5.C
【详解】分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.
详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有种方法,因为,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.
点睛:古典概型中基本事件数的探求方法:(1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.
6.C
【分析】由对立事件的定义判断A;应用列举法求、判断B、C;根据独立事件的判定判断D.
【详解】由事件定义,事件A与事件B可以同时发生,故不互为对立事件,A错误;
抛掷一枚骰子两次的样本点数共36种,
事件B的样本点为
,,,,,,,,,,,,,,,,,共18种,
事件C的样本点为,,,,,,,,,,,共有12种,
事件BC的样本点为,,,,,共6种,
所以,B错误;,C正确;
因为,所以事件B与事件C相互独立,D错误.
故选:C
7.B
【分析】连接ON,利用空间向量基本定理可得答案.
【详解】连接ON,.
故选:B.
8.A
【分析】根据余弦定理求出AC,再由勾股定理得BC⊥AC,以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,如图,利用空间向量法求出线线角的余弦值和异面直线夹角的范围,进而得出结果.
【详解】在直三棱柱中,,,,
由余弦定理,得,
所以,所以BC⊥AC,
以C为原点,CB为x轴,CA为y轴,为z轴,建立空间直角坐标系,如图,
,,,,
,,
设异面直线、所成角的平面角为,
有,又,
所以.
故选:A
9.AD
【分析】由向量共面的条件判断A,由数量积的性质判断B,由向量垂直判断C,由向量的加法法则判断D
【详解】
对于A:空间中任意两个非零向量,可以构成一个平面,故A正确;
对于B:向量的数量积不满足结合律,故B错误;
对于C:当,,互相垂直时,C错误;
对于D:根据向量的加法法则可知:,
故,故D正确;
故选:AD
10.ABC
【分析】分直线过原点,直线截距相等,直线截距互为相反数三种情况设直线分别为,,,结合过点可得答案.
【详解】当直线l过原点时,设直线方程为,因过点,则直线l的方程为,即,故A正确;
当直线l截距相等时,设直线方程为,因过点,则,则直线l的方程为,故C正确;
当直线l截距互为相反数时,设直线方程为,因过点,则,则直线l的方程为,故B正确.
故选:ABC.
11.BC
【分析】转化条件为圆的半径大于圆心到直线的距离加一即可得解.
【详解】圆的圆心到直线的距离,
因为圆上恒有4个点到直线的距离为1,
所以圆的半径.
对比选项,可得BC符合题意.
故选:BC.
12.AC
【分析】根据题意结合古典概型求,,,再结合概率的运算和事件的独立性运算求解.
【详解】
对于选项A:因为第二次取出球为3,4,5,6,所以,故A正确;
对于选项B:因为,所以,故B错误;
对于选项C:因为,则,
所以,故C正确;
对于选项D:因为,所以事件A与B不独立,故D错误;
故选:AC.
13.
【分析】根据平面向量数量积的坐标表示公式进行求解即可.
【详解】设,所以,,
因此由,
所以点P的轨迹方程为,
故答案为:
14.
【分析】列举出所有的基本事件,确定所求事件所包含的基本事件数,利用古典概型的概率公式可求得所求事件的概率.
【详解】设事件A为“抽到的2张卡片的数字之和不小于8”,
则这个试验的样本空间可记为,共包含9个样本点,
事件A包含的样本点有:、、,包含3个样本点,所以.
故答案为:.
15.
【分析】利用基向量表示,结合空间向量基本定理可得.
【详解】
所以,,所以.
【点睛】本题主要考查空间向量的基本定理,把目标向量向基底向量靠拢是求解的主要思路.
16.
【分析】直线过定点,曲线表示以O为圆心,2为半径的上半圆,数形结合可求实数k的取值范围.
【详解】直线l:,得,可知直线l过定点,
如图,曲线表示以O为圆心,2为半径的上半圆.
当直线l与半圆相切时,,解得.
曲线与x轴负半轴交于点,.
因为直线l与曲线有两个交点,所以.
故答案为:.
17.(1) (2)
【分析】
(1)首先利用直线与BC平行得到斜率,再利用点斜式写出方程即可.
(2)首先求出AC的斜率,再利用垂直得出直线斜率,最后用点斜式即可求出方程.
【详解】
(1)因为,,
所以直线BC的斜率为,则过点且与直线BC平行的直线方程为,即.
(2)因为直线AC的斜率为,
所以△ABC中AC边上的高所在直线的斜率为,
又高所在直线过点,所以高所在直线的方程为,
即.
18.(1)0.6;(2).
【分析】
(1)根据题设得到产品编号与综合指标Q的表格,应用古典概型的概率求法求一等品率;
(2)列举法求事件B的概率即可.
【详解】
(1)由题设可得如下表格,
产品编号
Q 2 4 8 3 6 5 3 2 1 6
又则核定该产品为一等品,故一等品共有6个,所以一等品率为;
(2)由题意,一等品中随机抽取2件产品有
,,,,,,,,,,,,,,共15种,
其中事件B为,,,,,,,,,,共10种
所以.
19.(1)29;32.5 (2)
【分析】
(1)根据平均数和中位数的定义即可求解;
(2)根据频率分布直方图可计算得到未成活颗数在和的数量,采用列举法可得所有基本事件和满足题意的基本事件个数,利用古典概型概率公式可计算得到结果.
【详解】
(1)根据频率分布直方图可估计平均数为:
.
根据频率分布直方图可估计中位数为:
(2)由频率分布直方图可知:未成活棵数在的班级有4个,记为A,B,C,D;未成活棵数在的班级有2个,记为a,b;
从“重点教授劳动技术班级”中随机抽取两个,则有AB,AC,AD,Aa,Ab,BC,BD,Ba,Bb,CD,Ca,Cb,Da,Db,ab,共15种情况;
其中有且仅有一个“重点教授劳动技术班级”在的情况有Aa,Ab,Ba,Bb,Ca,Cb,Da,Db,共8种情况;
所以所求概率.
20.(1)证明见解析 (2)1∶1
【分析】
(1)连接AC交BD于点M,连接EM,即可得到PA∥EM,从而得证;
(2)依题意可得AD⊥BD,如图建立空间直角坐标系,求出平面BDE的法向量,设,利用空间向量法求出线面角的正弦值,即可得到方程,解得,即可得解;
【详解】
(1)证明:如图,连接AC交BD于点M,连接EM,
因为M是AC的中点,E是PC的中点,所以PA∥EM
又平面BDE,平面BDE,
所以PA∥平面BDE
(2)解:因为,,所以,所以AD⊥BD,故以D为坐标原点,DA为x轴,DB为y轴,DP为z轴建立空间直角坐标系,
则,,,,,,
,,
设平面BDE的法向量为,则,即,
故取,设,则,
因为直线DF与平面BDE所成角的大小为30°,
所以,即
解得,故此时.
21.
(1),轨迹是以为圆心,2为半径的圆.
(2)或
【分析】
(1)设,利用两点距离公式列方程,整理化简即可得M的轨迹C的方程;
(2)若D是AB中点,连接CD,结合几何法及圆的弦长求C到直线l距离,数形结合及点线距离公式求参数,即得直线方程.
【详解】
(1)令,则,故2,整理得,
即M的轨迹C的方程为,轨迹是以为圆心,2为半径的圆.
(2)由题设,若D是AB中点,连接CD,则CD⊥AB,且,
所以,即C到直线l距离为1,
显然时满足C到直线l距离为1,且过;
若l的斜率存在,令l:,则,故,
所以,故l:;
综上,直线l为或.
22.(1)证明见解析 (2)
【分析】
(1)根据平面与平面垂直的性质定理和判定定理即可证明;
(2)根据条件建立空间直角坐标系,求出平面PBC和平面PCD的法向量,进而可求出结果.
【详解】
(1)证明:在正方形ABCD中,AD⊥AB.
又因为平面PAB⊥底面ABCD,平面平面,平面ABCD,
所以AD⊥平面PAB,
而平面PAD,所以平面PAB⊥平面PAD.
(2)设AC与BD交于点O,则平面平面,
在平面PAC内作AH垂直PO于H,
又因为平面PBD⊥平面PAC,
所以AH⊥平面PBD,而平面PBD,所以AH⊥BD,
又AC⊥BD,且,AH,平面PAC,所以BD⊥平面PAC,
因为平面PAC,所以BD⊥PA,
由(1)知AD⊥平面PAB,平面PAB,所以AD⊥PA,
又,AD,底面ABCD,
所以AP⊥底面ABCD,故PC和底面ABCD所成的角为∠PCA,即,
故.
以A为原点,的方向为x轴正方向,的方向为y轴正方向,的方向为z轴正方向建立空间直角坐标系A-xyz.
设,.则,,,,
所以,,,,
设平面PBC和平面PCD的法向量分别为,,
由,即,
取,得;
由,即,
取,得.
所以,,,
设二面角B-PC-D的大小为,则.
所以二面角B-PC-D的正弦值为.
固始县2023-2024学年高二上学期期中考试
数学试题
(考试用时120分钟 试卷满分150分)
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应科目的答案标号涂黑。如需改动,橡皮擦干净后,涂上其他答案标号。
3.回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将答题卡交回。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若直线:与:平行,则两直线之间的距离为( )
A. B.1 C. D.2
2.在x,y轴上的截距分别为4,的直线l被圆C:截得的弦长为( )
A.3 B.6 C. D.
3.已知圆心为的圆与直线相切,则该圆的标准方程是( )
A. B.
C. D.
4.已知,,,若平面ABC的一个法向量为,则( )
A. B. C. D.
5.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
A. B. C. D.
6.抛掷一枚质地均匀的骰子两次,设“第一次向上的点数是2”为事件A,“第二次向上的点数是奇数”为事件B,“两次向上的点数之和能被3整除”为事件C,则下列说法正确的是( )
A.事件A与事件B互为对立事件 B.
C. D.事件B与事件C相互不独立
7.如图,在四面体OABC中,,,.点M在OA上,且,N为BC中点,则等于( )
A. B. C. D.
8.已知直三棱柱,在中,,,,则异面直线与所成角为( )
A. B. C. D.
二、多项选择题(本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得3分,有选错的得0分)
9.判断下列结论正确的是( )
A.空间中任意两个非零向量,共面.
B.在三个向量的数量积运算中.
C.对于非零向量,由数量积,则.
D.若A,B,C,D是空间任意四点,则有.
10.已知直线l过点,且直线l在坐标轴上的截距的绝对值相等,则直线l的方程为( )
A. B. C. D.
11.若圆上恒有4个点到直线的距离为1,则实数r的可能取值是( )
A. B. C.3 D.
12.不透明的袋子中装有6个大小质地相同的小球,分别标有数字1,2,3,4,5,6,从中有放回的随机抽取两次,每次取一个球.A表示事件“第二次取出的球上标有的数字大于等于3”,B表示事件“两次取出的球上标有的数字之和为5,则( )
A. B. C. D.事件A与B相互独立
第Ⅱ卷(非选择题,共90分)
三、填空题:(本大题共4小题,每小题5分,共20分.把答案填写在题中横线上)
13.已知两点,,点P满足,则点P的轨迹方程为 .
14.现有3张分别标有1、3、5的卡片,采取有放回的方式从中依次随机取出2张卡片,则抽到的2张卡片的数字之和不小于8的概率是 .
15.如图,在正四面体P-ABC中,M,N分别为PA,BC的中点,D是线段MN上一点,且,若,则的值为 .
16.已知直线l:与曲线有两个交点,则k的取值范围为 .
四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.已知△ABC三个顶点的坐标分别为,,.求:
(1)过点且与直线BC平行的直线方程.
(2)△ABC中,AC边上的高所在直线的方程.
18.药品监督局检测某种产品的两个质量指标x,y,用综合指标核定该产品的等级.若,则核定该产品为一等品.现从一批该产品中随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
质量指标
产品编号
质量指标
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件B为“在抽取的2件产品中,每件产品的综合指标均满足”,求事件B的概率.
19.为全面贯彻落实习近平总书记“培养德智体美劳全面发展的社会主义建设者和接班人”的指示精神和中共中央国务院印发的《关于全面加强新时代大中小学劳动教育的意见》的文件要求.南充高中建成以“种桑养蚕”为主题的学生劳动实践基地,该基地于2023年4月在南充高中高坪校区完工,基地包括桑树基地和养蚕基地.现学校给高中10个班每班划分一块实践基地用于种植桑树,经过一段时间的维护,根据这10个班桑树未存活的数量绘制如下频率分布直方图,桑树未存活数量凡超过30棵的班级,设为需“重点教授劳动技术班级”.
(1)根据直方图估计这10个班级的未存活桑树的平均数和中位数;
(2)现从“重点教授劳动技术班级”中随机抽取两个班级调查其劳动课上课情况,求抽出来的班级中有且仅有一个“重点教授劳动技术班级”在的概率.
20.如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PD⊥平面ABCD,E是棱PC的中点.
(1)证明:PA∥平面BDE;
(2)若,,且F为棱PB上一点,DF与平面BDE所成角的大小为30°,求的值.
21.已知△POM满足,,
(1)求点M的轨迹C的方程,并说明轨迹的形状.
(2)若直线l过定点与C交于A,B两点,且,求直线l的方程.
22.如图,在四棱锥P-ABCD中,底面ABCD是正方形,平面PAB⊥底面ABCD,侧棱PC与底面所成的角为60°.
(1)证明:平面PAB⊥平面PAD;
(2)若平面PBD⊥平面PAC,求二面角B-PC-D的正弦值.
参考答案:
1.C
【分析】根据两直线平行可得,再由平行线间的距离公式即可求得结果.
【详解】依题意,由两直线平行可知,解得,
所以两直线分别为,,
可得两直线之间的距离为,
故选:C.
2.B
【分析】根据题意,求得直线l的方程为,结合圆的弦长公式,即可求解.
【详解】由题意得,直线l的方程为,即,
又由C:,可化为,
可得圆C的圆心为,半径为,则圆心到直线l的距离,
所以直线l被圆C截得的弦长为.
故选:B.
3.A
【分析】由圆心到切线的距离等于半径,求出圆的半径,即可得到本题答案.
【详解】因为圆心为的圆与直线相切,所以圆心到直线的距离等于半径,
即,
所以该圆的标准方程是.
故选:A
4.C
【分析】利用法向量和平面内直线的方向向量之间的关系求解即可.
【详解】由,,得:
,,
面ABC的一个法向量为,
所以,,
即,,
解得,,
所以,
故选:C.
5.C
【详解】分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.
详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有种方法,因为,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.
点睛:古典概型中基本事件数的探求方法:(1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.
6.C
【分析】由对立事件的定义判断A;应用列举法求、判断B、C;根据独立事件的判定判断D.
【详解】由事件定义,事件A与事件B可以同时发生,故不互为对立事件,A错误;
抛掷一枚骰子两次的样本点数共36种,
事件B的样本点为
,,,,,,,,,,,,,,,,,共18种,
事件C的样本点为,,,,,,,,,,,共有12种,
事件BC的样本点为,,,,,共6种,
所以,B错误;,C正确;
因为,所以事件B与事件C相互独立,D错误.
故选:C
7.B
【分析】连接ON,利用空间向量基本定理可得答案.
【详解】连接ON,.
故选:B.
8.A
【分析】根据余弦定理求出AC,再由勾股定理得BC⊥AC,以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,如图,利用空间向量法求出线线角的余弦值和异面直线夹角的范围,进而得出结果.
【详解】在直三棱柱中,,,,
由余弦定理,得,
所以,所以BC⊥AC,
以C为原点,CB为x轴,CA为y轴,为z轴,建立空间直角坐标系,如图,
,,,,
,,
设异面直线、所成角的平面角为,
有,又,
所以.
故选:A
9.AD
【分析】由向量共面的条件判断A,由数量积的性质判断B,由向量垂直判断C,由向量的加法法则判断D
【详解】
对于A:空间中任意两个非零向量,可以构成一个平面,故A正确;
对于B:向量的数量积不满足结合律,故B错误;
对于C:当,,互相垂直时,C错误;
对于D:根据向量的加法法则可知:,
故,故D正确;
故选:AD
10.ABC
【分析】分直线过原点,直线截距相等,直线截距互为相反数三种情况设直线分别为,,,结合过点可得答案.
【详解】当直线l过原点时,设直线方程为,因过点,则直线l的方程为,即,故A正确;
当直线l截距相等时,设直线方程为,因过点,则,则直线l的方程为,故C正确;
当直线l截距互为相反数时,设直线方程为,因过点,则,则直线l的方程为,故B正确.
故选:ABC.
11.BC
【分析】转化条件为圆的半径大于圆心到直线的距离加一即可得解.
【详解】圆的圆心到直线的距离,
因为圆上恒有4个点到直线的距离为1,
所以圆的半径.
对比选项,可得BC符合题意.
故选:BC.
12.AC
【分析】根据题意结合古典概型求,,,再结合概率的运算和事件的独立性运算求解.
【详解】
对于选项A:因为第二次取出球为3,4,5,6,所以,故A正确;
对于选项B:因为,所以,故B错误;
对于选项C:因为,则,
所以,故C正确;
对于选项D:因为,所以事件A与B不独立,故D错误;
故选:AC.
13.
【分析】根据平面向量数量积的坐标表示公式进行求解即可.
【详解】设,所以,,
因此由,
所以点P的轨迹方程为,
故答案为:
14.
【分析】列举出所有的基本事件,确定所求事件所包含的基本事件数,利用古典概型的概率公式可求得所求事件的概率.
【详解】设事件A为“抽到的2张卡片的数字之和不小于8”,
则这个试验的样本空间可记为,共包含9个样本点,
事件A包含的样本点有:、、,包含3个样本点,所以.
故答案为:.
15.
【分析】利用基向量表示,结合空间向量基本定理可得.
【详解】
所以,,所以.
【点睛】本题主要考查空间向量的基本定理,把目标向量向基底向量靠拢是求解的主要思路.
16.
【分析】直线过定点,曲线表示以O为圆心,2为半径的上半圆,数形结合可求实数k的取值范围.
【详解】直线l:,得,可知直线l过定点,
如图,曲线表示以O为圆心,2为半径的上半圆.
当直线l与半圆相切时,,解得.
曲线与x轴负半轴交于点,.
因为直线l与曲线有两个交点,所以.
故答案为:.
17.(1) (2)
【分析】
(1)首先利用直线与BC平行得到斜率,再利用点斜式写出方程即可.
(2)首先求出AC的斜率,再利用垂直得出直线斜率,最后用点斜式即可求出方程.
【详解】
(1)因为,,
所以直线BC的斜率为,则过点且与直线BC平行的直线方程为,即.
(2)因为直线AC的斜率为,
所以△ABC中AC边上的高所在直线的斜率为,
又高所在直线过点,所以高所在直线的方程为,
即.
18.(1)0.6;(2).
【分析】
(1)根据题设得到产品编号与综合指标Q的表格,应用古典概型的概率求法求一等品率;
(2)列举法求事件B的概率即可.
【详解】
(1)由题设可得如下表格,
产品编号
Q 2 4 8 3 6 5 3 2 1 6
又则核定该产品为一等品,故一等品共有6个,所以一等品率为;
(2)由题意,一等品中随机抽取2件产品有
,,,,,,,,,,,,,,共15种,
其中事件B为,,,,,,,,,,共10种
所以.
19.(1)29;32.5 (2)
【分析】
(1)根据平均数和中位数的定义即可求解;
(2)根据频率分布直方图可计算得到未成活颗数在和的数量,采用列举法可得所有基本事件和满足题意的基本事件个数,利用古典概型概率公式可计算得到结果.
【详解】
(1)根据频率分布直方图可估计平均数为:
.
根据频率分布直方图可估计中位数为:
(2)由频率分布直方图可知:未成活棵数在的班级有4个,记为A,B,C,D;未成活棵数在的班级有2个,记为a,b;
从“重点教授劳动技术班级”中随机抽取两个,则有AB,AC,AD,Aa,Ab,BC,BD,Ba,Bb,CD,Ca,Cb,Da,Db,ab,共15种情况;
其中有且仅有一个“重点教授劳动技术班级”在的情况有Aa,Ab,Ba,Bb,Ca,Cb,Da,Db,共8种情况;
所以所求概率.
20.(1)证明见解析 (2)1∶1
【分析】
(1)连接AC交BD于点M,连接EM,即可得到PA∥EM,从而得证;
(2)依题意可得AD⊥BD,如图建立空间直角坐标系,求出平面BDE的法向量,设,利用空间向量法求出线面角的正弦值,即可得到方程,解得,即可得解;
【详解】
(1)证明:如图,连接AC交BD于点M,连接EM,
因为M是AC的中点,E是PC的中点,所以PA∥EM
又平面BDE,平面BDE,
所以PA∥平面BDE
(2)解:因为,,所以,所以AD⊥BD,故以D为坐标原点,DA为x轴,DB为y轴,DP为z轴建立空间直角坐标系,
则,,,,,,
,,
设平面BDE的法向量为,则,即,
故取,设,则,
因为直线DF与平面BDE所成角的大小为30°,
所以,即
解得,故此时.
21.
(1),轨迹是以为圆心,2为半径的圆.
(2)或
【分析】
(1)设,利用两点距离公式列方程,整理化简即可得M的轨迹C的方程;
(2)若D是AB中点,连接CD,结合几何法及圆的弦长求C到直线l距离,数形结合及点线距离公式求参数,即得直线方程.
【详解】
(1)令,则,故2,整理得,
即M的轨迹C的方程为,轨迹是以为圆心,2为半径的圆.
(2)由题设,若D是AB中点,连接CD,则CD⊥AB,且,
所以,即C到直线l距离为1,
显然时满足C到直线l距离为1,且过;
若l的斜率存在,令l:,则,故,
所以,故l:;
综上,直线l为或.
22.(1)证明见解析 (2)
【分析】
(1)根据平面与平面垂直的性质定理和判定定理即可证明;
(2)根据条件建立空间直角坐标系,求出平面PBC和平面PCD的法向量,进而可求出结果.
【详解】
(1)证明:在正方形ABCD中,AD⊥AB.
又因为平面PAB⊥底面ABCD,平面平面,平面ABCD,
所以AD⊥平面PAB,
而平面PAD,所以平面PAB⊥平面PAD.
(2)设AC与BD交于点O,则平面平面,
在平面PAC内作AH垂直PO于H,
又因为平面PBD⊥平面PAC,
所以AH⊥平面PBD,而平面PBD,所以AH⊥BD,
又AC⊥BD,且,AH,平面PAC,所以BD⊥平面PAC,
因为平面PAC,所以BD⊥PA,
由(1)知AD⊥平面PAB,平面PAB,所以AD⊥PA,
又,AD,底面ABCD,
所以AP⊥底面ABCD,故PC和底面ABCD所成的角为∠PCA,即,
故.
以A为原点,的方向为x轴正方向,的方向为y轴正方向,的方向为z轴正方向建立空间直角坐标系A-xyz.
设,.则,,,,
所以,,,,
设平面PBC和平面PCD的法向量分别为,,
由,即,
取,得;
由,即,
取,得.
所以,,,
设二面角B-PC-D的大小为,则.
所以二面角B-PC-D的正弦值为.
同课章节目录
