北师大版六年级上册数学圆周率的历史(课件)(共17张PPT)
文档属性
| 名称 | 北师大版六年级上册数学圆周率的历史(课件)(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-17 16:17:42 | ||
图片预览



文档简介
(共17张PPT)
北师大版 六年级上册 第一单元《圆》
圆周率的历史
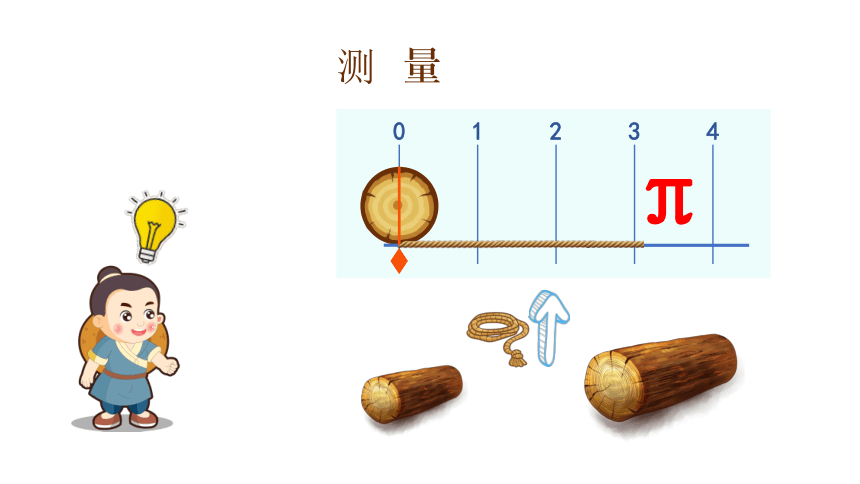
要多长的木料才够做这个轮子呢?
?
木直中绳,輮以为轮
周长
直径
=
直径
周长
直径
=
=
测 量
0
1
2
3
4
π
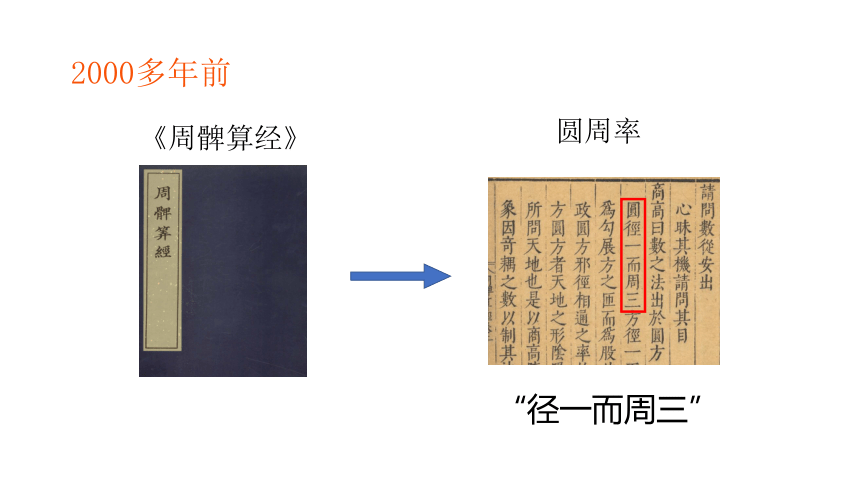
“径一而周三”
2000多年前
《周髀算经》
圆周率
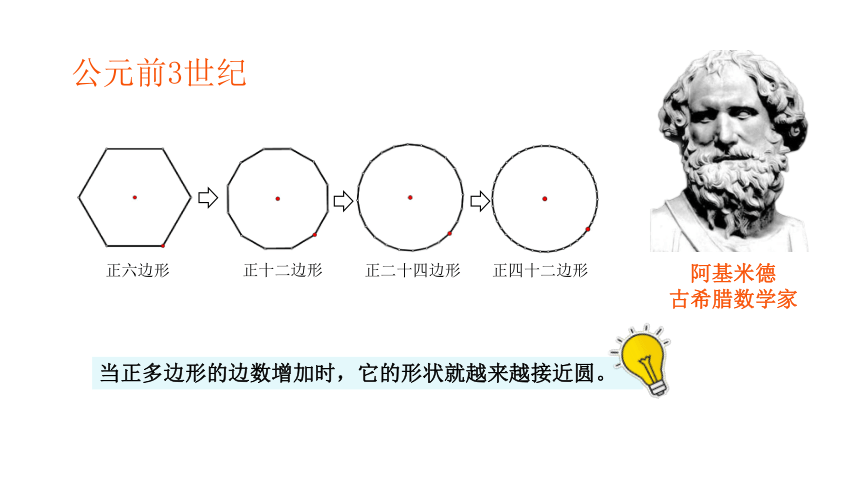
公元前3世纪
正六边形
正十二边形
正二十四边形
正四十二边形
阿基米德
古希腊数学家
当正多边形的边数增加时,它的形状就越来越接近圆。
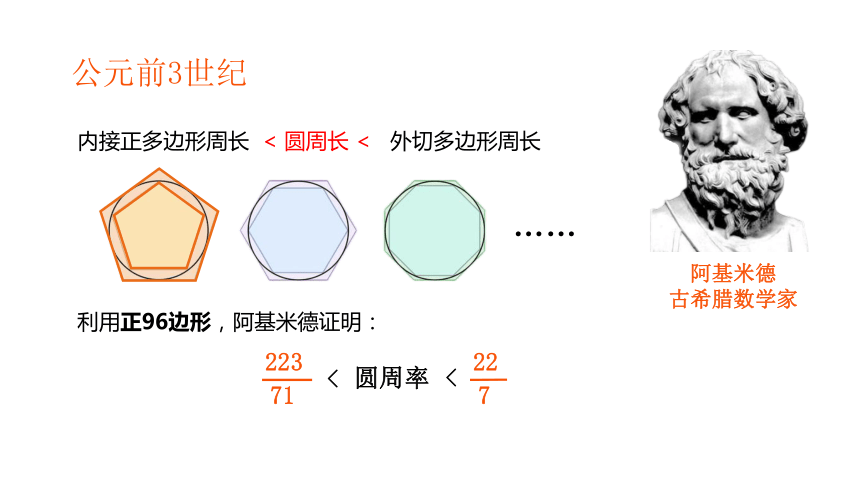
公元前3世纪
阿基米德
古希腊数学家
……
圆周率
223
71
22
7
利用正96边形,阿基米德证明:
内接正多边形周长
<
<
外切多边形周长
< 圆周长 <
公元3世纪(魏晋时期)
刘徽
(约公元225年—295年)
割圆术
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”
公元3世纪(魏晋时期)
刘徽
(约公元225年—295年)
割圆术
公元3世纪(魏晋时期)
刘徽
(约公元225年—295年)
正3072边形
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”
徽率 : 3.1416
割圆术
……
1500多年前(南北朝)
祖冲之
(公元429年-500年)
圆周率
355
113
约率:
密率:
π
22
7
<
3.1415926
<
3.1415927
“古之九数,圆周率三,圆径率一,其术疏舛。自刘歆、张衡、皮延宗之徒,各设新率,未臻折衷。宋末,南徐州从事史祖冲之更开密法,以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽;肭数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈肭二限之间。密率:圆径一百一十三,圆周三百五十五。约率:圆径七,周二十二。”
1500多年前(南北朝)
祖冲之
(公元429年-500年)
祖冲之
李淳风
1500多年前(南北朝)
祖冲之
(公元429年-500年)
16000多边形
π
<
3.1415926
<
3.1415927
1500多年前(南北朝)
祖冲之
(公元429年-500年)
3.1415926 <π< 3.1415927
在世界上领先了约1000年。
前20世纪 埃及 (16÷9)2 ≈ 3.1605
前19世纪 巴比伦 25÷8 = 3.125
前12世纪 中国 3
前5世纪 圣经 3
前250年 阿基米德 3.140845 3.142857(22/7)
263 刘徽 3.14159
5世纪 祖冲之 3.1415926 3.1415927
1400 Madhava 10 位
1706 Machin 100 位
1947 808 位
1961 100265 位
1987 1 亿位
1999 2061 亿位
2010 2.7 万亿位
2016 22.4 万亿位
2021 62.8 万亿位
……
求π的世界纪录
现代……
现在计算π的值已经被人们用来测试或检验超级计算机的各项性能,特别是用来测试运算速度与计算过程的稳定性。
圆周率的历史
2021年
1500年前
公元3世纪
公元前3世纪
2000年前
周髀算经
小数点后
62.8万亿位
3.14
3
3.1415927
~
3.1415927
北师大版 六年级上册 第一单元《圆》
圆周率的历史
要多长的木料才够做这个轮子呢?
?
木直中绳,輮以为轮
周长
直径
=
直径
周长
直径
=
=
测 量
0
1
2
3
4
π
“径一而周三”
2000多年前
《周髀算经》
圆周率
公元前3世纪
正六边形
正十二边形
正二十四边形
正四十二边形
阿基米德
古希腊数学家
当正多边形的边数增加时,它的形状就越来越接近圆。
公元前3世纪
阿基米德
古希腊数学家
……
圆周率
223
71
22
7
利用正96边形,阿基米德证明:
内接正多边形周长
<
<
外切多边形周长
< 圆周长 <
公元3世纪(魏晋时期)
刘徽
(约公元225年—295年)
割圆术
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”
公元3世纪(魏晋时期)
刘徽
(约公元225年—295年)
割圆术
公元3世纪(魏晋时期)
刘徽
(约公元225年—295年)
正3072边形
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”
徽率 : 3.1416
割圆术
……
1500多年前(南北朝)
祖冲之
(公元429年-500年)
圆周率
355
113
约率:
密率:
π
22
7
<
3.1415926
<
3.1415927
“古之九数,圆周率三,圆径率一,其术疏舛。自刘歆、张衡、皮延宗之徒,各设新率,未臻折衷。宋末,南徐州从事史祖冲之更开密法,以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽;肭数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈肭二限之间。密率:圆径一百一十三,圆周三百五十五。约率:圆径七,周二十二。”
1500多年前(南北朝)
祖冲之
(公元429年-500年)
祖冲之
李淳风
1500多年前(南北朝)
祖冲之
(公元429年-500年)
16000多边形
π
<
3.1415926
<
3.1415927
1500多年前(南北朝)
祖冲之
(公元429年-500年)
3.1415926 <π< 3.1415927
在世界上领先了约1000年。
前20世纪 埃及 (16÷9)2 ≈ 3.1605
前19世纪 巴比伦 25÷8 = 3.125
前12世纪 中国 3
前5世纪 圣经 3
前250年 阿基米德 3.140845 3.142857(22/7)
263 刘徽 3.14159
5世纪 祖冲之 3.1415926 3.1415927
1400 Madhava 10 位
1706 Machin 100 位
1947 808 位
1961 100265 位
1987 1 亿位
1999 2061 亿位
2010 2.7 万亿位
2016 22.4 万亿位
2021 62.8 万亿位
……
求π的世界纪录
现代……
现在计算π的值已经被人们用来测试或检验超级计算机的各项性能,特别是用来测试运算速度与计算过程的稳定性。
圆周率的历史
2021年
1500年前
公元3世纪
公元前3世纪
2000年前
周髀算经
小数点后
62.8万亿位
3.14
3
3.1415927
~
3.1415927
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
