24.4弧长及扇形的面积 同步练习(含答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.4弧长及扇形的面积 同步练习(含答案)2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 440.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 11:06:41 | ||
图片预览


文档简介
24.4弧长及扇形的面积同步练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.时钟的分针长5cm,经过15分钟,它的针尖转过的弧长是( )
A.πcm B.πcm C.πcm D.πcm
2.一段圆弧的半径是12,弧长是 ,则这段圆弧所对的圆心角是( )
A. B. C. D.
3.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A. π B. π C. π D. π
4.如图,以AB为直径,点O为圆心的半圆经过点C.若AC=BC=2,则图中阴影部分的面积是( ).
A. B. C. D.
5.如图所示,以AB为直径的半圆,绕点B顺时针旋转60°,点A旋转到点A′,且AB=4,则图中阴影部分的面积是( )
A. B. C.8 D.
6.已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( )
A.π B.3π C.π D.π
7.如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,∠AOB= ∠COB,⊙O的半径为 ,连接AC交OB于点E,则图中阴影部分面积是( )
A. B. C. D.
8.如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径总长度为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知扇形的圆心角为120°,弧长为6π,则它的半径为 .
10.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 的长为 (保留π)
11.如图是2022年杭州亚运会徽标的示意图,若,,,则阴影部分面积为 .
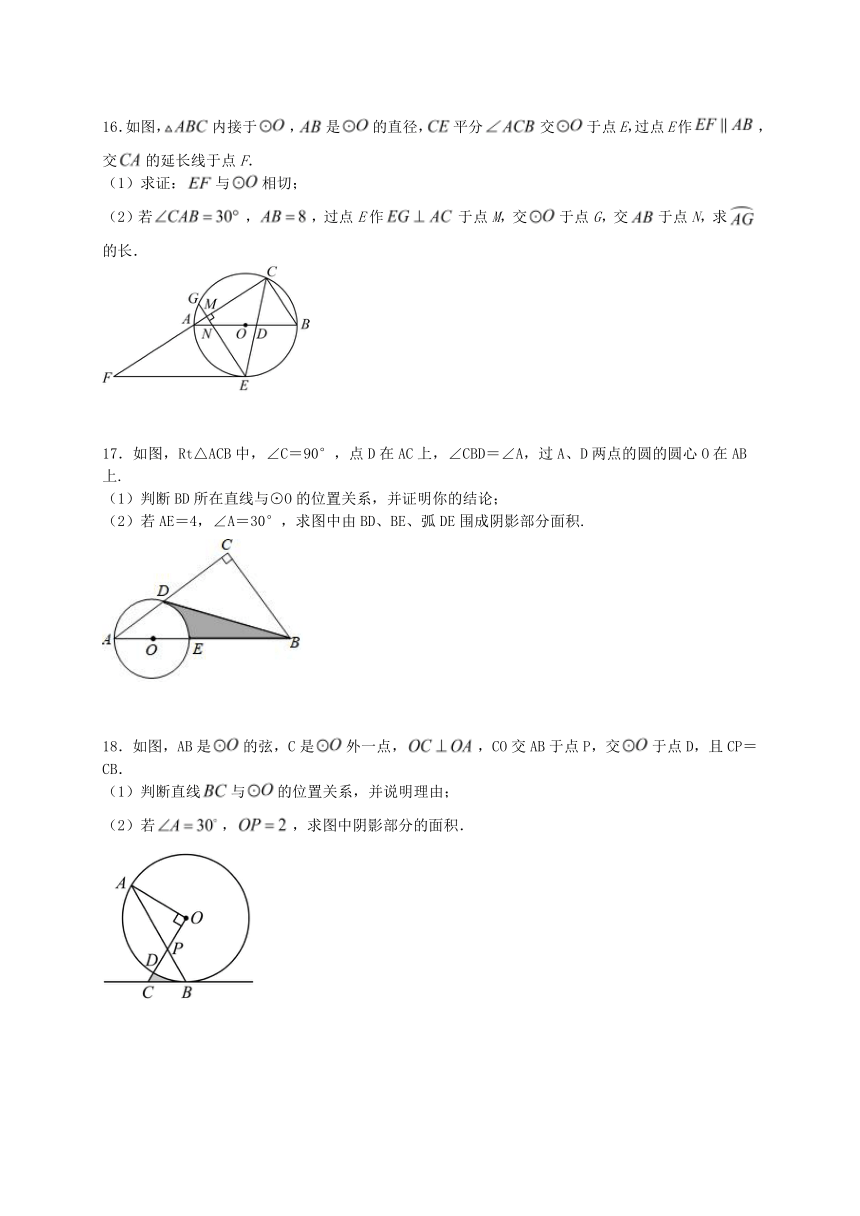
12.如图,在矩形中,,分别以点、为圆心,为半径画弧,与边分别交于点、,且与对角线交于同一点,则图中阴影部分的面积为 .
13.如图,在中,,若将绕点顺时针旋转,点的对应点为点,点的对应点为点,点为的中点,连接.则点的运动路径与线段、围成的阴影部分面积是 .
三、解答题:(本题共5题,共45分)
14.如图,AB是⊙O的直径,点C在⊙O上.若∠A=30°,OA=2,求劣弧AC的长.
15.如图,已知⊙O的半径为8cm,点A为半径OB的延长线上一点,射线AC切⊙O于点C, 的长为 ,求线段AB的长.
16.如图,内接于,是的直径,平分交于点E,过点E作,交的延长线于点F.
(1)求证:与相切;
(2)若,,过点E作于点M,交于点G,交于点N,求的长.
17.如图,Rt△ACB中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
(1)判断BD所在直线与⊙O的位置关系,并证明你的结论;
(2)若AE=4,∠A=30°,求图中由BD、BE、弧DE围成阴影部分面积.
18.如图,AB是的弦,C是外一点,,CO交AB于点P,交于点D,且CP=CB.
(1)判断直线与的位置关系,并说明理由;
(2)若,,求图中阴影部分的面积.
参考答案:
1.C2.A3.B4.C5.B6.C7.D8.D
9.9
10.
11.
12.
13.
14.解: ∵∠A=30°,
∴∠COB=2∠A=60°,
∴∠AOC=180°-∠COB=120°,
∴ 劣弧AC的长= ,
15.依题意知,OC⊥AC.
∴∠ACO=90°;∠AOC= ,
∴∠A=90°-60°=30°,
∴OA= ,
∴AB=AO-OB=16-8=8cm
16.(1)证明:如图,连接,
是的直径,
,
平分交于点E,
,
,
,
,
,
是的半径,
与相切;
(2)解:如图,连接,,
,,
,
,
是等边三角形,
,
,
,,
,
,
,
,是的直径,
,
.
即的长为.
17.(1)解:直线BD与⊙O的位置关系是相切
证明:连接OD、DE
∵∠C=90°
∴∠CBD+∠CDB=90°
∵∠A=∠CBD
∴∠A+∠CDB=90°
∵OD=OA
∴∠A=∠ADO
∴∠ADO+∠CDB=90°
∴∠ODB=180°﹣90°=90°
∴OD⊥BD
∵OD为半径
∴BD是⊙O切线
(2)解:∵AE是⊙O直径
∴∠ADE=90°
∵AE=4,∠A=30°
∴DE=AE=2,∠AED=60°
∵OD=OE
∴△DOE是等边三角形
∴∠ODE=60°,OD=OE=DE=2
∵∠ODB=90°
∴∠EDB=30°
∴∠B=∠DEO﹣∠EDB=60°﹣30°=30°
∴OB=2OD=4
由勾股定理得:DB=,
∴阴影部分的面积S=S△ODB﹣S扇形DOE
=
=.
18.(1)解:直线BC与⊙O相切,
理由:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵CP=CB,
∴∠CPB=∠CBP,
∵∠CPB=∠APO,
∴∠CBP=∠APO,
∵,
∴∠AOC=90°,
在Rt△AOP中,
∵∠OAB +∠APO=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=90°,
∴OB⊥CB,
又∵OB是半径,
∴CB与⊙O相切;
(2)解:∵∠A=30°,∠AOP=90°,OP=2,
∴∠APO=60°,AP=2OP=4,
∴AO=BO,
∵OA=OB,
∴∠OBA=∠A=30°,
∴∠BOP=∠APO﹣∠OBA=30°=∠OBP,
∴OP=PB=2,
∵∠BPD=∠APO=60°,PC=CB,
∴△PBC是等边三角形,
∴∠PCB=∠CBP=60°,
∴BC=PB=2,
∴图中阴影部分的面积=S△OBC﹣S扇形OBD2×2π
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.时钟的分针长5cm,经过15分钟,它的针尖转过的弧长是( )
A.πcm B.πcm C.πcm D.πcm
2.一段圆弧的半径是12,弧长是 ,则这段圆弧所对的圆心角是( )
A. B. C. D.
3.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A. π B. π C. π D. π
4.如图,以AB为直径,点O为圆心的半圆经过点C.若AC=BC=2,则图中阴影部分的面积是( ).
A. B. C. D.
5.如图所示,以AB为直径的半圆,绕点B顺时针旋转60°,点A旋转到点A′,且AB=4,则图中阴影部分的面积是( )
A. B. C.8 D.
6.已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( )
A.π B.3π C.π D.π
7.如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,∠AOB= ∠COB,⊙O的半径为 ,连接AC交OB于点E,则图中阴影部分面积是( )
A. B. C. D.
8.如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径总长度为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知扇形的圆心角为120°,弧长为6π,则它的半径为 .
10.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 的长为 (保留π)
11.如图是2022年杭州亚运会徽标的示意图,若,,,则阴影部分面积为 .
12.如图,在矩形中,,分别以点、为圆心,为半径画弧,与边分别交于点、,且与对角线交于同一点,则图中阴影部分的面积为 .
13.如图,在中,,若将绕点顺时针旋转,点的对应点为点,点的对应点为点,点为的中点,连接.则点的运动路径与线段、围成的阴影部分面积是 .
三、解答题:(本题共5题,共45分)
14.如图,AB是⊙O的直径,点C在⊙O上.若∠A=30°,OA=2,求劣弧AC的长.
15.如图,已知⊙O的半径为8cm,点A为半径OB的延长线上一点,射线AC切⊙O于点C, 的长为 ,求线段AB的长.
16.如图,内接于,是的直径,平分交于点E,过点E作,交的延长线于点F.
(1)求证:与相切;
(2)若,,过点E作于点M,交于点G,交于点N,求的长.
17.如图,Rt△ACB中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
(1)判断BD所在直线与⊙O的位置关系,并证明你的结论;
(2)若AE=4,∠A=30°,求图中由BD、BE、弧DE围成阴影部分面积.
18.如图,AB是的弦,C是外一点,,CO交AB于点P,交于点D,且CP=CB.
(1)判断直线与的位置关系,并说明理由;
(2)若,,求图中阴影部分的面积.
参考答案:
1.C2.A3.B4.C5.B6.C7.D8.D
9.9
10.
11.
12.
13.
14.解: ∵∠A=30°,
∴∠COB=2∠A=60°,
∴∠AOC=180°-∠COB=120°,
∴ 劣弧AC的长= ,
15.依题意知,OC⊥AC.
∴∠ACO=90°;∠AOC= ,
∴∠A=90°-60°=30°,
∴OA= ,
∴AB=AO-OB=16-8=8cm
16.(1)证明:如图,连接,
是的直径,
,
平分交于点E,
,
,
,
,
,
是的半径,
与相切;
(2)解:如图,连接,,
,,
,
,
是等边三角形,
,
,
,,
,
,
,
,是的直径,
,
.
即的长为.
17.(1)解:直线BD与⊙O的位置关系是相切
证明:连接OD、DE
∵∠C=90°
∴∠CBD+∠CDB=90°
∵∠A=∠CBD
∴∠A+∠CDB=90°
∵OD=OA
∴∠A=∠ADO
∴∠ADO+∠CDB=90°
∴∠ODB=180°﹣90°=90°
∴OD⊥BD
∵OD为半径
∴BD是⊙O切线
(2)解:∵AE是⊙O直径
∴∠ADE=90°
∵AE=4,∠A=30°
∴DE=AE=2,∠AED=60°
∵OD=OE
∴△DOE是等边三角形
∴∠ODE=60°,OD=OE=DE=2
∵∠ODB=90°
∴∠EDB=30°
∴∠B=∠DEO﹣∠EDB=60°﹣30°=30°
∴OB=2OD=4
由勾股定理得:DB=,
∴阴影部分的面积S=S△ODB﹣S扇形DOE
=
=.
18.(1)解:直线BC与⊙O相切,
理由:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵CP=CB,
∴∠CPB=∠CBP,
∵∠CPB=∠APO,
∴∠CBP=∠APO,
∵,
∴∠AOC=90°,
在Rt△AOP中,
∵∠OAB +∠APO=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=90°,
∴OB⊥CB,
又∵OB是半径,
∴CB与⊙O相切;
(2)解:∵∠A=30°,∠AOP=90°,OP=2,
∴∠APO=60°,AP=2OP=4,
∴AO=BO,
∵OA=OB,
∴∠OBA=∠A=30°,
∴∠BOP=∠APO﹣∠OBA=30°=∠OBP,
∴OP=PB=2,
∵∠BPD=∠APO=60°,PC=CB,
∴△PBC是等边三角形,
∴∠PCB=∠CBP=60°,
∴BC=PB=2,
∴图中阴影部分的面积=S△OBC﹣S扇形OBD2×2π
同课章节目录
