三 角 函 数 的 图 象 和 性 质
文档属性
| 名称 | 三 角 函 数 的 图 象 和 性 质 |  | |
| 格式 | rar | ||
| 文件大小 | 214.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-04 12:12:00 | ||
图片预览




文档简介
课件17张PPT。 数 学
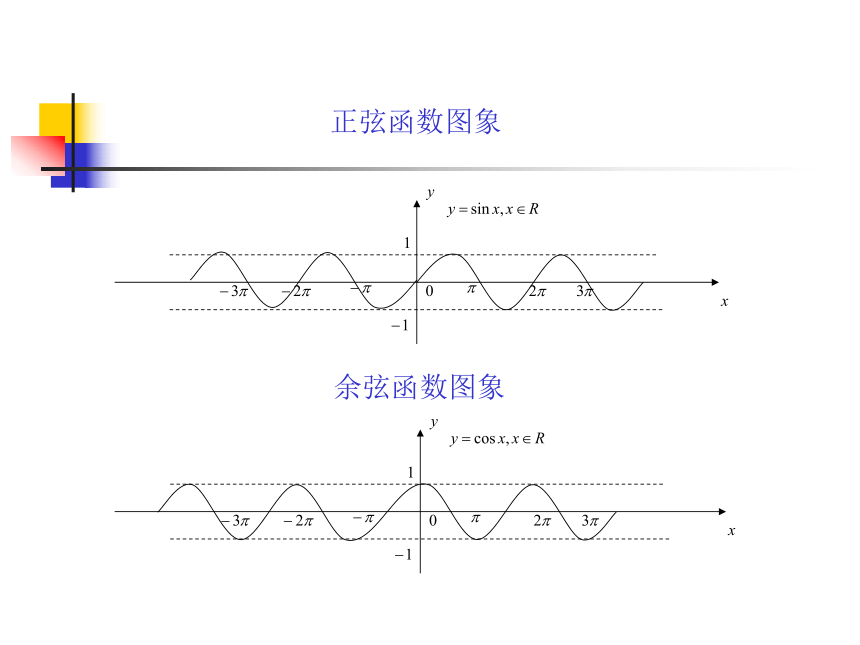
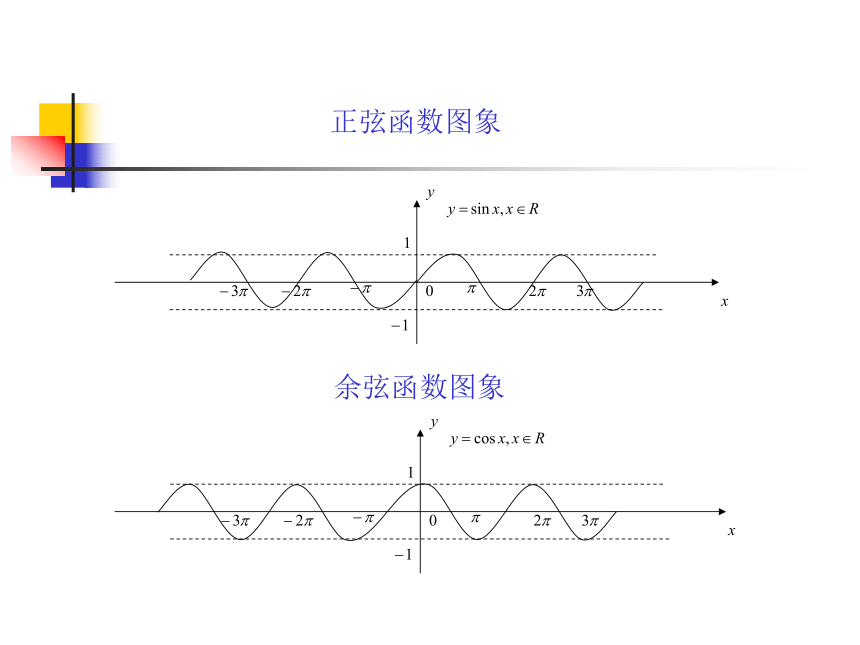
第一册(下)三 角 函 数 的 图 象 和 性 质数学组正弦函数.余弦函数的性质授课老师:正弦函数图象余弦函数图象正弦函数图象余弦函数图象(2)值域
正弦线、余弦线的长度小于或等于单位圆的半径的长度,
所以 即
这就说明正弦函数、余弦函数的值域都是 ,其中正弦函数当且
仅当 取得最大值1,
当且仅当 取得最小值-1,
而余弦函数当且仅当 取得最大值1,
当且仅当 取得最小值-1,
练习
(1)求函数 y = Sin 2x 的定义域.
(2)求函数 y = √sin x 及 y = √2sin x 的值域
____________答案
(1) R (2) [ 0, 1 ], [ –√2, √2 ]
例1 画出下列函数的简图解(1)按五个关键点列表,利用正弦函数的性质描点画图(2)按五个关键点列表,利用余弦函数的性质描点画图例2 求使下列函数取得最大值的自变量x的集合,并说出最大值是什么。
(1) Y = cosx +1, x∈R;
(2) Y = sin2x, x∈R;(2)令 ,那么 必须并且只需 ,且使函数
取得最大值的 的集合是
由得:
这就是说,使函数 取得最大值的 的集合是
函数 的最大值是1 课堂练习教科书第56页练习 3题(1)(2),
4题第4题答案
当X∈{X︱X=?∏+2k∏,k∈Z}时,函数Y取得最小值-2;
当X∈{X︱X=6K∏,k∈Z}时,函数Y取得最小值1;
归 纳 总 结(1) 正弦.余弦函数的定义域为R,值域均为[ -1, 1 ]
(2) 用归纳.比较的数学思想,掌握较复杂的正弦.余弦 函数的五点作图法以及平移.对称变换的作图原理.作业布置
P57 1.(3) , 2 , 9再 见
第一册(下)三 角 函 数 的 图 象 和 性 质数学组正弦函数.余弦函数的性质授课老师:正弦函数图象余弦函数图象正弦函数图象余弦函数图象(2)值域
正弦线、余弦线的长度小于或等于单位圆的半径的长度,
所以 即
这就说明正弦函数、余弦函数的值域都是 ,其中正弦函数当且
仅当 取得最大值1,
当且仅当 取得最小值-1,
而余弦函数当且仅当 取得最大值1,
当且仅当 取得最小值-1,
练习
(1)求函数 y = Sin 2x 的定义域.
(2)求函数 y = √sin x 及 y = √2sin x 的值域
____________答案
(1) R (2) [ 0, 1 ], [ –√2, √2 ]
例1 画出下列函数的简图解(1)按五个关键点列表,利用正弦函数的性质描点画图(2)按五个关键点列表,利用余弦函数的性质描点画图例2 求使下列函数取得最大值的自变量x的集合,并说出最大值是什么。
(1) Y = cosx +1, x∈R;
(2) Y = sin2x, x∈R;(2)令 ,那么 必须并且只需 ,且使函数
取得最大值的 的集合是
由得:
这就是说,使函数 取得最大值的 的集合是
函数 的最大值是1 课堂练习教科书第56页练习 3题(1)(2),
4题第4题答案
当X∈{X︱X=?∏+2k∏,k∈Z}时,函数Y取得最小值-2;
当X∈{X︱X=6K∏,k∈Z}时,函数Y取得最小值1;
归 纳 总 结(1) 正弦.余弦函数的定义域为R,值域均为[ -1, 1 ]
(2) 用归纳.比较的数学思想,掌握较复杂的正弦.余弦 函数的五点作图法以及平移.对称变换的作图原理.作业布置
P57 1.(3) , 2 , 9再 见
