2023-—2024学年冀教版数学八年级上册 第十三章 全等三角形 全章综合测评卷(含答案解析)
文档属性
| 名称 | 2023-—2024学年冀教版数学八年级上册 第十三章 全等三角形 全章综合测评卷(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 459.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 08:47:20 | ||
图片预览




文档简介
第十三章 全等三角形
作答时间:120分钟 总分:120分
一、选择题(本大题有16个小题,每小题3分,共48分)
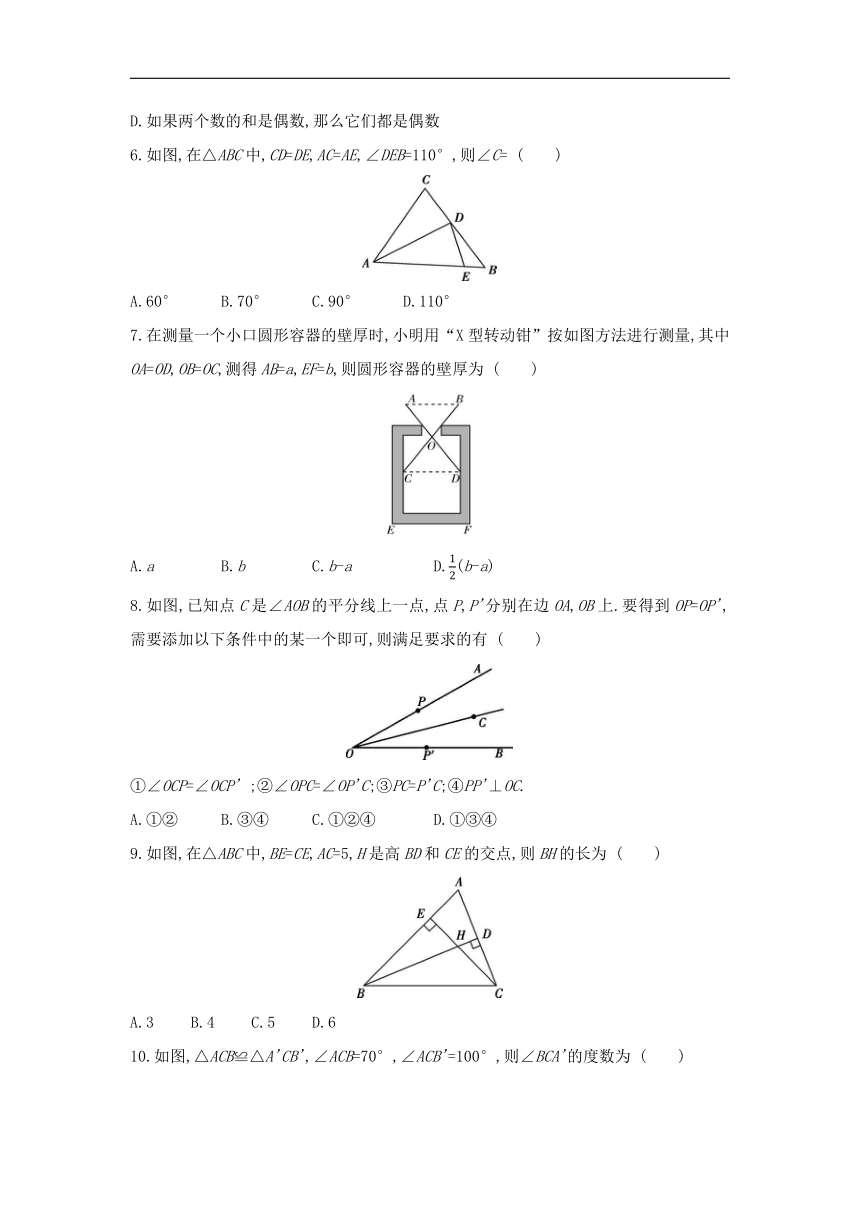
1.在下列各组图形中,是全等图形的是 ( )
2.已知图中的两个三角形全等,则∠1等于 ( )
A.50° B.60° C.70° D.120°
3.嘉淇发现有两个结论:在△A1B1C1与△A2B2C2中,①若A1B1=A2B2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2. 对于上述的两个结论,下列说法正确的是 ( )
A.①,②都错误 B.①,②都正确
C.①正确,②错误 D.①错误,②正确
4.嘉淇同学不慎将一块三角形玻璃摔碎成如图所示的四块,聪明的嘉淇经过仔细地考虑,认为只要带其中的两块碎片去玻璃店就可以配出与原来一样的玻璃.则下列四个答案中考虑最全面的是 ( )
A.带其中的任意两块去都可以
B.带1,2或2,3去就可以了
C.带1,4或3,4去就可以了
D.带1,4或2,4或3,4去均可
5.下列命题与它的逆命题都为真命题的是 ( )
A.已知非零数x,如果为分式,那么它的倒数也是分式
B.如果x的相反数为7,那么x为-7
C.如果一个数能被8整除,那么这个数也能被4整除
D.如果两个数的和是偶数,那么它们都是偶数
6.如图,在△ABC中,CD=DE,AC=AE,∠DEB=110°,则∠C= ( )
A.60° B.70° C.90° D.110°
7.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,则圆形容器的壁厚为 ( )
A.a B.b C.b-a D.(b-a)
8.如图,已知点C是∠AOB的平分线上一点,点P,P'分别在边OA,OB上.要得到OP=OP',需要添加以下条件中的某一个即可,则满足要求的有 ( )
①∠OCP=∠OCP' ;②∠OPC=∠OP'C;③PC=P'C;④PP'⊥OC.
A.①② B.③④ C.①②④ D.①③④
9.如图,在△ABC中,BE=CE,AC=5,H是高BD和CE的交点,则BH的长为 ( )
A.3 B.4 C.5 D.6
10.如图,△ACB≌△A'CB',∠ACB=70°,∠ACB'=100°,则∠BCA'的度数为 ( )
A.30° B.35° C.40° D.50°
11.如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为 ( )
A.a+c B.b+c
C.a-b+c D.a+b-c
12.如图,已知∠AOB.按照以下步骤作图:①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于C,D两点,连接CD.②分别以点C,D为圆心,以大于线段OC的长为半径作弧,两弧在∠AOB内交于点E,连接CE,DE.③连接OE交CD于点M.下列结论中错误的是 ( )
A.∠CEO=∠DEO B.CM=MD
C.∠OCD=∠ECD D.S四边形OCED=CD·OE
13.如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位长度的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为( )
A.3或5 B.5或7 C.7 D.3或7
14. 如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE平分∠ABC,则以下结论中不正确的有 ( )
①BC+AD=AB;②E为CD的中点;③∠AEB=90°;④S△ABE=S四边形ABCD.
A.0个 B.1个 C.2个 D.3个
15.如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是 ( )
16.如图,在△ABC中,E,F分别在AB,AC上,DE⊥DF,D是BC的中点,则BE+CF与EF的大小关系是 ( )
A.BE+CF>EF B.BE+CF=EF
C.BE+CF二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有2个空,每空3分)
17.当空调安装在墙上时,一般都会用如图所示的方法固定在墙上.这种方法应用的数学知识是 .
18.如图,△ABC和△ADE为两个共直角顶点的等腰直角三角形,∠BAC=∠DAE=90°,连接CD,BE.则图中一定与线段CD相等的线段是 .
19.已知点C为线段AB上一点,分别以AC,BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB= .
(2)如图2,若∠ACD=α,则∠AFB= . (用含α的代数式表示).
三、解答题(本大题有5个小题,共60分)
20.(8分)如图,在△ABC中,点E是AB延长线上一点,且BE=AB.
(1)尺规作图:在∠CBE内作射线BD,使BD∥AC.(保留作图痕迹,不要求写作法)
(2)在BD上取点F,使BF=AC,连接EF,求证△ABC≌△BEF.
21.(10分)如图,小刚站在河边的点A处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向以相同的步子走了30步到达一棵树C处,接着向前走了30步到达D处,然后向正南方向直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约为50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.
22.(12分)如图,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,连接BF.
(1)求证:△AEF≌△DEC.
(2)若D是BC的中点,求证:BF=AD.
23.(14分)如图,在△ABC中,AD⊥AB,AD=AB,AE⊥AC,AE=AC.
(1)求证:△ACD≌△AEB.
(2)若∠ACB=90°,判断CD与BE的位置关系,请说明理由.
24.(16分)已知直角三角形OAB和直角三角形OCD的直角顶点O重合,∠AOB=∠COD=90°,且OA=OB,OC=OD.
(1)如图1,当点C,D分别在OA,OB上时,AC与BD的数量关系是AC BD(填“>”“<”或“=”),AC与BD的位置关系是AC BD(填“∥”或“⊥”).
(2)将直角三角形OCD绕点O顺时针旋转,使点D在OA上,如图2,连接AC,BD,求证:AC=BD.
(3)现将直角三角形OCD绕点O顺时针继续旋转,如图3,连接AC,BD,猜想AC与BD的数量关系和位置关系,并给出证明.
参考答案
一、选择题
1.C
2.A 【解析】 如图,由题意,知△ABC≌△A'B'C',所以∠B'=∠B=70°,所以∠1=180°-∠A'-∠B'=50°.故选A.
3.C 【解析】 ①符合“SSS”,故正确;②为“ASS”,不能判定三角形全等,故错误.故选C.
4.D 【解析】 带1,4或3,4可以用“ASA”确定三角形全等,带2,4直接延长边可还原出原三角形.故选D.
5.B 【解析】 A项, 的倒数是,不是分式,原命题是假命题,不符合题意.B项,如果x的相反数为7,那么x为-7,是真命题,逆命题:如果x为-7,那么x的相反数为7,是真命题,符合题意.C项,如果一个数能被8整除,那么这个数也能被4整除,是真命题,逆命题:如果一个数能被4整除,那么这个数也能被8整除,是假命题,不符合题意.D项,因为两个奇数的和也是偶数,所以原命题是假命题,不符合题意.故选B.
6.B 【解析】 在△ADC和△ADE中,∴△ADC≌△ADE(SSS),∴∠C=∠AED=180°-∠DEB=70°.故选B.
7.D 【解析】 在△AOB和△DOC中,所以△AOB≌△DOC(SAS),所以AB=CD=a,因为EF=b,所以圆形容器的壁厚为(b-a).故选D.
8.C 【解析】 如图,连接CP,CP',PP'.若加①∠OCP=∠OCP',则根据“ASA”可证明△OPC≌△OP'C,得OP=OP';若加②∠OPC=∠OP'C,则根据“AAS”可证明△OPC≌△OP'C,得OP=OP';若加③PC=P'C,则不能证明△OPC≌△OP'C,不能得到OP=OP';若加④PP'⊥OC,则根据“ASA”可证明△OPD≌△OP'D,得OP=OP'.故选C.
9.C 【解析】 ∵BD和CE是△ABC的高,∴∠ABD+∠A=90°,∠ACE+∠A=90°,∴∠ABD=
∠ACE.在△BEH和△CEA中,∴△BEH≌△CEA(ASA),∴BH=AC=5.故选C.
10.C 【解析】 解法一 ∵△ACB≌△A'CB',∠ACB=70°,∴∠A'CB'=∠ACB=70°,又∵∠ACB'=100°,∴∠ACA'=∠ACB'-∠A'CB'=100°-70°=30°,∴∠BCA'=∠ACB-∠ACA'=70°-30°=40°.故选C.
解法二 ∵∠ACB=70°,∠ACB'=100°,∴∠BCB'=∠ACB'-∠ACB=100°-70°=30°,
∵△ACB≌△A'CB',∴∠A'CB'=∠ACB=70°,∴∠BCA'=∠A'CB'-∠BCB'=70°-30°=40°.故选C.
11.D 【解析】 设BF交CD于点M,则∠BMC=∠DMF,∴∠B=∠D.在△ABF和△CDE中,∴△ABF≌△CDE,∴AF=CE=a,DE=BF=b,∴DF=DE-EF=b-c,∴AD=AF+FD=a+b-c.故选D.
12.C 【解析】 由作图步骤可知,OE是∠AOB的平分线,OC=OD,∴根据“SAS”可得△COE≌△DOE,△COM≌△DOM,∴∠CEO=∠DEO,CM=MD,∠CMO=∠DMO=90°,∴S四边形OCED=CD·OE.根据题意无法得出∠OCD=∠ECD.故选C.
13.D 【解析】 当点P在BC上且BP=CE时,在△ABP与△DCE中,∴△ABP≌△DCE,∴BP=t-2=1,∴t=3;当点P在DA上且AP=CE时,在△BAP与△DCE中,∴△BAP≌△DCE,∴AP=8-t=1,
∴t=7.综上, t的值为3或7.故选D.
14.A 【解析】 ∵AD∥BC,∴∠ABC+∠BAD=180°.∵AE,BE分别是∠BAD与∠ABC的平分线,∴∠BAE=∠BAD,∠ABE=∠ABC,∴∠BAE+∠ABE=(∠BAD+∠ABC)=90°,∴∠AEB=180°-(∠BAE+∠ABE)=180°-90°=90°,故③正确.如图,延长AE交BC的延长线于F,∵∠AEB=90°,∴BE⊥AF.∵BE平分∠ABC,∴∠ABE=∠FBE.在△ABE与△FBE中, ∴△ABE≌△FBE(ASA),∴AB=BF,AE=FE.∵AD∥BC,∴∠EAD=∠F.在△ADE与△FCE中,∴△ADE≌△FCE(ASA),∴AD=CF,∴AB=
BC+CF=BC+AD,故①正确.∵△ADE≌△FCE,∴CE=DE,即点E为CD的中点,故②正确.∵△ADE≌△FCE,∴S△ADE=S△FCE,∴S四边形ABCD=S△ABF.易得S△ABE=S△ABF,∴S△ABE=S四边形ABCD,故④正确.故选A.
15.C 【解析】 A项,由“SAS”可得两个小三角形全等,故A项不符合题意;B项,由“SAS”可得两个小三角形全等,故B项不符合题意;C项,如图1,因为∠B+∠BDE+∠BED=180°,∠BED+∠DEF+∠FEC=180°,∠B=∠DEF=x°,所以∠FEC=
∠BDE,所以BE和CF是对应边,而BD=CF=3,所以不能判定两个小三角形全等,故C项符合题意;D项,如图2,因为∠B+∠BDE+∠BED=180°,∠BED+∠DEF+∠FEC=180°,∠B=∠DEF=x°,所以∠FEC=∠BDE,又因为BD=CE=2,∠B=∠C,所以△BDE≌△CEF(ASA),故D项不符合题意.故选C.
16.A 【解析】 如图,延长ED至P,使DP=DE,连接FP,CP.∵D是BC的中点,∴BD=CD.在△BDE和△CDP中,∴△BDE≌△CDP(SAS),∴BE=CP.∵DE⊥DF,DE=DP,
DF=DF,∴△EDF≌△PDF(SAS),∴EF=PF.在△CFP中,CP+CF=BE+CF>FP=EF.故选A.
二、填空题
17.三角形具有稳定性
18.BE 【解析】 ∵△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∴∠BAC-∠BAD=∠DAE-∠BAD,即∠DAC=∠EAB.在△CAD和△BAE中, ∴△CAD≌△BAE(SAS),∴CD=BE.
19.120° 180°-α 【解析】 (1)如图1,∵∠ACD=∠BCE,∴∠ACE=∠DCB .在△ACE与△DCB 中, ∴△ACE≌△DCB (SAS),∴∠EAC=∠BDC ,∵∠AMC=∠DMF,∴∠AFD=∠ACD=60°,∴∠AFB=120°.(2)如图2,∵∠ACD=∠BCE,∴∠ACE=∠DCB.在△ACE与△DCB 中, ∴△ACE≌△DCB (SAS),∴∠EAC=∠BDC ,∵∠AMC=∠DMF,∴∠AFD=∠ACD=α,∴∠AFB=180°-α.
三、解答题
20.【解析】 (1)如图,射线BD即所求.
(2)如图,∵BD∥AC,∴∠EBF=∠A,
又∵BE=AB,BF=AC,
∴△ABC≌△BEF(SAS).
21.【解析】 (1)画出示意图如图所示.
(2)在△ABC和△DEC中,
所以△ABC≌△DEC(ASA),所以AB=DE.因为小刚共走了140步,其中在AD走了60步,所以走完DE用了80步,小刚一步大约为50厘米,即DE≈80×50=4 000(厘米)=40(米),
所以小刚在点A处时他与电线塔的距离约为40米.
22.【解析】 (1)∵AF∥BC,∴∠AFE=∠DCE.
∵点E为AD的中点,∴AE=DE.
在△AEF和△DEC中,
∴△AEF≌△DEC(AAS).
(2)由(1)知△AEF≌△DEC,∴FA=CD.
∵D是BC的中点,∴BD=CD,∴AF=BD.
∵AF∥BC,∴∠BAF=∠ABD.
在△ABF和△BAD中,
∴△ABF≌△BAD(SAS),∴BF=AD.
23.【解析】 (1)∵AD⊥AB,AE⊥AC,
∴∠DAB=∠CAE=90°,∴∠DAC=∠BAE.
在△ACD与△AEB中,
∴△ACD≌△AEB.
(2)CD⊥BE.理由如下:
如图,延长DC,EB交于点F,
∵∠ACB=90°,∠CAE=90°,
∴BC∥AE,∴∠CBF=∠AEB.
∵△ACD≌△AEB,∴∠ACD=∠AEB,∴∠CBF=∠ACD.
∵∠ACD+∠BCF=180°-∠ACB=90°,
∴∠CBF+∠BCF=90°,∴∠F=90°,∴CD⊥BE.
24.【解析】 (1)= ⊥
∵OA=OB,OC=OD,
∴OA-OC=OB-OD,∴AC=BD.
∵∠AOB=∠COD=90°,∴AO⊥BO,
∵点C,D分别在OA,OB上,∴AC⊥BD.
(2)在△OCA和△ODB中,
∴△OCA≌△ODB,∴AC=BD.
(3)AC=BD,AC⊥BD.理由如下:
如图,∵∠AOB=∠COD=90°,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠AOC=∠BOD.
在△OCA和△ODB中,
∴△OCA≌△ODB,∴AC=BD,∠BDO=∠ACO,
∵∠ACO+∠CFO=90°,∠CFO=∠DFE,
∴∠BDO+∠DFE=90°,
∴∠DEF=180°-90°=90°,∴AC⊥BD.
作答时间:120分钟 总分:120分
一、选择题(本大题有16个小题,每小题3分,共48分)
1.在下列各组图形中,是全等图形的是 ( )
2.已知图中的两个三角形全等,则∠1等于 ( )
A.50° B.60° C.70° D.120°
3.嘉淇发现有两个结论:在△A1B1C1与△A2B2C2中,①若A1B1=A2B2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,A1C1=A2C2,B1C1=B2C2,则△A1B1C1≌△A2B2C2. 对于上述的两个结论,下列说法正确的是 ( )
A.①,②都错误 B.①,②都正确
C.①正确,②错误 D.①错误,②正确
4.嘉淇同学不慎将一块三角形玻璃摔碎成如图所示的四块,聪明的嘉淇经过仔细地考虑,认为只要带其中的两块碎片去玻璃店就可以配出与原来一样的玻璃.则下列四个答案中考虑最全面的是 ( )
A.带其中的任意两块去都可以
B.带1,2或2,3去就可以了
C.带1,4或3,4去就可以了
D.带1,4或2,4或3,4去均可
5.下列命题与它的逆命题都为真命题的是 ( )
A.已知非零数x,如果为分式,那么它的倒数也是分式
B.如果x的相反数为7,那么x为-7
C.如果一个数能被8整除,那么这个数也能被4整除
D.如果两个数的和是偶数,那么它们都是偶数
6.如图,在△ABC中,CD=DE,AC=AE,∠DEB=110°,则∠C= ( )
A.60° B.70° C.90° D.110°
7.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,则圆形容器的壁厚为 ( )
A.a B.b C.b-a D.(b-a)
8.如图,已知点C是∠AOB的平分线上一点,点P,P'分别在边OA,OB上.要得到OP=OP',需要添加以下条件中的某一个即可,则满足要求的有 ( )
①∠OCP=∠OCP' ;②∠OPC=∠OP'C;③PC=P'C;④PP'⊥OC.
A.①② B.③④ C.①②④ D.①③④
9.如图,在△ABC中,BE=CE,AC=5,H是高BD和CE的交点,则BH的长为 ( )
A.3 B.4 C.5 D.6
10.如图,△ACB≌△A'CB',∠ACB=70°,∠ACB'=100°,则∠BCA'的度数为 ( )
A.30° B.35° C.40° D.50°
11.如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为 ( )
A.a+c B.b+c
C.a-b+c D.a+b-c
12.如图,已知∠AOB.按照以下步骤作图:①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于C,D两点,连接CD.②分别以点C,D为圆心,以大于线段OC的长为半径作弧,两弧在∠AOB内交于点E,连接CE,DE.③连接OE交CD于点M.下列结论中错误的是 ( )
A.∠CEO=∠DEO B.CM=MD
C.∠OCD=∠ECD D.S四边形OCED=CD·OE
13.如图,在正方形ABCD中,AB=2,延长BC到点E,使CE=1,连接DE,动点P从点A出发以每秒1个单位长度的速度沿AB→BC→CD→DA向终点A运动,设点P的运动时间为t秒,当△ABP和△DCE全等时,t的值为( )
A.3或5 B.5或7 C.7 D.3或7
14. 如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE平分∠ABC,则以下结论中不正确的有 ( )
①BC+AD=AB;②E为CD的中点;③∠AEB=90°;④S△ABE=S四边形ABCD.
A.0个 B.1个 C.2个 D.3个
15.如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是 ( )
16.如图,在△ABC中,E,F分别在AB,AC上,DE⊥DF,D是BC的中点,则BE+CF与EF的大小关系是 ( )
A.BE+CF>EF B.BE+CF=EF
C.BE+CF
17.当空调安装在墙上时,一般都会用如图所示的方法固定在墙上.这种方法应用的数学知识是 .
18.如图,△ABC和△ADE为两个共直角顶点的等腰直角三角形,∠BAC=∠DAE=90°,连接CD,BE.则图中一定与线段CD相等的线段是 .
19.已知点C为线段AB上一点,分别以AC,BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB= .
(2)如图2,若∠ACD=α,则∠AFB= . (用含α的代数式表示).
三、解答题(本大题有5个小题,共60分)
20.(8分)如图,在△ABC中,点E是AB延长线上一点,且BE=AB.
(1)尺规作图:在∠CBE内作射线BD,使BD∥AC.(保留作图痕迹,不要求写作法)
(2)在BD上取点F,使BF=AC,连接EF,求证△ABC≌△BEF.
21.(10分)如图,小刚站在河边的点A处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向以相同的步子走了30步到达一棵树C处,接着向前走了30步到达D处,然后向正南方向直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约为50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.
22.(12分)如图,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,连接BF.
(1)求证:△AEF≌△DEC.
(2)若D是BC的中点,求证:BF=AD.
23.(14分)如图,在△ABC中,AD⊥AB,AD=AB,AE⊥AC,AE=AC.
(1)求证:△ACD≌△AEB.
(2)若∠ACB=90°,判断CD与BE的位置关系,请说明理由.
24.(16分)已知直角三角形OAB和直角三角形OCD的直角顶点O重合,∠AOB=∠COD=90°,且OA=OB,OC=OD.
(1)如图1,当点C,D分别在OA,OB上时,AC与BD的数量关系是AC BD(填“>”“<”或“=”),AC与BD的位置关系是AC BD(填“∥”或“⊥”).
(2)将直角三角形OCD绕点O顺时针旋转,使点D在OA上,如图2,连接AC,BD,求证:AC=BD.
(3)现将直角三角形OCD绕点O顺时针继续旋转,如图3,连接AC,BD,猜想AC与BD的数量关系和位置关系,并给出证明.
参考答案
一、选择题
1.C
2.A 【解析】 如图,由题意,知△ABC≌△A'B'C',所以∠B'=∠B=70°,所以∠1=180°-∠A'-∠B'=50°.故选A.
3.C 【解析】 ①符合“SSS”,故正确;②为“ASS”,不能判定三角形全等,故错误.故选C.
4.D 【解析】 带1,4或3,4可以用“ASA”确定三角形全等,带2,4直接延长边可还原出原三角形.故选D.
5.B 【解析】 A项, 的倒数是,不是分式,原命题是假命题,不符合题意.B项,如果x的相反数为7,那么x为-7,是真命题,逆命题:如果x为-7,那么x的相反数为7,是真命题,符合题意.C项,如果一个数能被8整除,那么这个数也能被4整除,是真命题,逆命题:如果一个数能被4整除,那么这个数也能被8整除,是假命题,不符合题意.D项,因为两个奇数的和也是偶数,所以原命题是假命题,不符合题意.故选B.
6.B 【解析】 在△ADC和△ADE中,∴△ADC≌△ADE(SSS),∴∠C=∠AED=180°-∠DEB=70°.故选B.
7.D 【解析】 在△AOB和△DOC中,所以△AOB≌△DOC(SAS),所以AB=CD=a,因为EF=b,所以圆形容器的壁厚为(b-a).故选D.
8.C 【解析】 如图,连接CP,CP',PP'.若加①∠OCP=∠OCP',则根据“ASA”可证明△OPC≌△OP'C,得OP=OP';若加②∠OPC=∠OP'C,则根据“AAS”可证明△OPC≌△OP'C,得OP=OP';若加③PC=P'C,则不能证明△OPC≌△OP'C,不能得到OP=OP';若加④PP'⊥OC,则根据“ASA”可证明△OPD≌△OP'D,得OP=OP'.故选C.
9.C 【解析】 ∵BD和CE是△ABC的高,∴∠ABD+∠A=90°,∠ACE+∠A=90°,∴∠ABD=
∠ACE.在△BEH和△CEA中,∴△BEH≌△CEA(ASA),∴BH=AC=5.故选C.
10.C 【解析】 解法一 ∵△ACB≌△A'CB',∠ACB=70°,∴∠A'CB'=∠ACB=70°,又∵∠ACB'=100°,∴∠ACA'=∠ACB'-∠A'CB'=100°-70°=30°,∴∠BCA'=∠ACB-∠ACA'=70°-30°=40°.故选C.
解法二 ∵∠ACB=70°,∠ACB'=100°,∴∠BCB'=∠ACB'-∠ACB=100°-70°=30°,
∵△ACB≌△A'CB',∴∠A'CB'=∠ACB=70°,∴∠BCA'=∠A'CB'-∠BCB'=70°-30°=40°.故选C.
11.D 【解析】 设BF交CD于点M,则∠BMC=∠DMF,∴∠B=∠D.在△ABF和△CDE中,∴△ABF≌△CDE,∴AF=CE=a,DE=BF=b,∴DF=DE-EF=b-c,∴AD=AF+FD=a+b-c.故选D.
12.C 【解析】 由作图步骤可知,OE是∠AOB的平分线,OC=OD,∴根据“SAS”可得△COE≌△DOE,△COM≌△DOM,∴∠CEO=∠DEO,CM=MD,∠CMO=∠DMO=90°,∴S四边形OCED=CD·OE.根据题意无法得出∠OCD=∠ECD.故选C.
13.D 【解析】 当点P在BC上且BP=CE时,在△ABP与△DCE中,∴△ABP≌△DCE,∴BP=t-2=1,∴t=3;当点P在DA上且AP=CE时,在△BAP与△DCE中,∴△BAP≌△DCE,∴AP=8-t=1,
∴t=7.综上, t的值为3或7.故选D.
14.A 【解析】 ∵AD∥BC,∴∠ABC+∠BAD=180°.∵AE,BE分别是∠BAD与∠ABC的平分线,∴∠BAE=∠BAD,∠ABE=∠ABC,∴∠BAE+∠ABE=(∠BAD+∠ABC)=90°,∴∠AEB=180°-(∠BAE+∠ABE)=180°-90°=90°,故③正确.如图,延长AE交BC的延长线于F,∵∠AEB=90°,∴BE⊥AF.∵BE平分∠ABC,∴∠ABE=∠FBE.在△ABE与△FBE中, ∴△ABE≌△FBE(ASA),∴AB=BF,AE=FE.∵AD∥BC,∴∠EAD=∠F.在△ADE与△FCE中,∴△ADE≌△FCE(ASA),∴AD=CF,∴AB=
BC+CF=BC+AD,故①正确.∵△ADE≌△FCE,∴CE=DE,即点E为CD的中点,故②正确.∵△ADE≌△FCE,∴S△ADE=S△FCE,∴S四边形ABCD=S△ABF.易得S△ABE=S△ABF,∴S△ABE=S四边形ABCD,故④正确.故选A.
15.C 【解析】 A项,由“SAS”可得两个小三角形全等,故A项不符合题意;B项,由“SAS”可得两个小三角形全等,故B项不符合题意;C项,如图1,因为∠B+∠BDE+∠BED=180°,∠BED+∠DEF+∠FEC=180°,∠B=∠DEF=x°,所以∠FEC=
∠BDE,所以BE和CF是对应边,而BD=CF=3,所以不能判定两个小三角形全等,故C项符合题意;D项,如图2,因为∠B+∠BDE+∠BED=180°,∠BED+∠DEF+∠FEC=180°,∠B=∠DEF=x°,所以∠FEC=∠BDE,又因为BD=CE=2,∠B=∠C,所以△BDE≌△CEF(ASA),故D项不符合题意.故选C.
16.A 【解析】 如图,延长ED至P,使DP=DE,连接FP,CP.∵D是BC的中点,∴BD=CD.在△BDE和△CDP中,∴△BDE≌△CDP(SAS),∴BE=CP.∵DE⊥DF,DE=DP,
DF=DF,∴△EDF≌△PDF(SAS),∴EF=PF.在△CFP中,CP+CF=BE+CF>FP=EF.故选A.
二、填空题
17.三角形具有稳定性
18.BE 【解析】 ∵△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∴∠BAC-∠BAD=∠DAE-∠BAD,即∠DAC=∠EAB.在△CAD和△BAE中, ∴△CAD≌△BAE(SAS),∴CD=BE.
19.120° 180°-α 【解析】 (1)如图1,∵∠ACD=∠BCE,∴∠ACE=∠DCB .在△ACE与△DCB 中, ∴△ACE≌△DCB (SAS),∴∠EAC=∠BDC ,∵∠AMC=∠DMF,∴∠AFD=∠ACD=60°,∴∠AFB=120°.(2)如图2,∵∠ACD=∠BCE,∴∠ACE=∠DCB.在△ACE与△DCB 中, ∴△ACE≌△DCB (SAS),∴∠EAC=∠BDC ,∵∠AMC=∠DMF,∴∠AFD=∠ACD=α,∴∠AFB=180°-α.
三、解答题
20.【解析】 (1)如图,射线BD即所求.
(2)如图,∵BD∥AC,∴∠EBF=∠A,
又∵BE=AB,BF=AC,
∴△ABC≌△BEF(SAS).
21.【解析】 (1)画出示意图如图所示.
(2)在△ABC和△DEC中,
所以△ABC≌△DEC(ASA),所以AB=DE.因为小刚共走了140步,其中在AD走了60步,所以走完DE用了80步,小刚一步大约为50厘米,即DE≈80×50=4 000(厘米)=40(米),
所以小刚在点A处时他与电线塔的距离约为40米.
22.【解析】 (1)∵AF∥BC,∴∠AFE=∠DCE.
∵点E为AD的中点,∴AE=DE.
在△AEF和△DEC中,
∴△AEF≌△DEC(AAS).
(2)由(1)知△AEF≌△DEC,∴FA=CD.
∵D是BC的中点,∴BD=CD,∴AF=BD.
∵AF∥BC,∴∠BAF=∠ABD.
在△ABF和△BAD中,
∴△ABF≌△BAD(SAS),∴BF=AD.
23.【解析】 (1)∵AD⊥AB,AE⊥AC,
∴∠DAB=∠CAE=90°,∴∠DAC=∠BAE.
在△ACD与△AEB中,
∴△ACD≌△AEB.
(2)CD⊥BE.理由如下:
如图,延长DC,EB交于点F,
∵∠ACB=90°,∠CAE=90°,
∴BC∥AE,∴∠CBF=∠AEB.
∵△ACD≌△AEB,∴∠ACD=∠AEB,∴∠CBF=∠ACD.
∵∠ACD+∠BCF=180°-∠ACB=90°,
∴∠CBF+∠BCF=90°,∴∠F=90°,∴CD⊥BE.
24.【解析】 (1)= ⊥
∵OA=OB,OC=OD,
∴OA-OC=OB-OD,∴AC=BD.
∵∠AOB=∠COD=90°,∴AO⊥BO,
∵点C,D分别在OA,OB上,∴AC⊥BD.
(2)在△OCA和△ODB中,
∴△OCA≌△ODB,∴AC=BD.
(3)AC=BD,AC⊥BD.理由如下:
如图,∵∠AOB=∠COD=90°,
∴∠AOB+∠AOD=∠COD+∠AOD,
∴∠AOC=∠BOD.
在△OCA和△ODB中,
∴△OCA≌△ODB,∴AC=BD,∠BDO=∠ACO,
∵∠ACO+∠CFO=90°,∠CFO=∠DFE,
∴∠BDO+∠DFE=90°,
∴∠DEF=180°-90°=90°,∴AC⊥BD.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
