安徽省阜阳市2023-2024学年沪科版九年级上学期期中数学试题(含答案)
文档属性
| 名称 | 安徽省阜阳市2023-2024学年沪科版九年级上学期期中数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 529.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 11:32:58 | ||
图片预览



文档简介
2023-2024学年度第一学期九年级阶段性评价
数学(泸科版)
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分)
1.已知线段a=4,b=6,如果线段b是线段a和c的比例中项那么线段c的长度是( )
A. B.8 C.9 D.10
2.若抛物线经过A(-2,6),B(8,6)两点,则抛物线的对称轴为( )
A.直线 B.直线 C.直线 D.直线
3.对于抛物线的说法正确的是( )
A.开口向上 B.顶点坐标是(1,-2)
C.对称轴是直线x=1 D.当x<-1时,y随x的增大而增大
4.已知两个相似三角形的相似比为2:3,则它们的周长的比为( )
A.4:9 B.3:2 C.2:3 D.4:6
5.已知某抛物线与二次函数的图象的开口大小相同,开口方向相反,且顶点坐标为(1,2023),则该抛物线对应的函数表达式为( )
A. B.
C. D.
6.如图,已知D、E分别在△ABC的AB、AC边上,△ABC∽△AED,则下列各式成立的是( )
第6题图
A. B.
C. D..
7.如图所示,是一个长20m、宽16m的矩形花园,根据需要将它的长缩短xm、宽增加xm,要想使修改后的花园面积达到最大,则x应为( )
第7题图
A.1 B.1.5 C.2 D.4
8.如图,在平行四边形ABCD中,AE:BE=1:2,若,则( )
第8题图
A.27 B.18 C.9 D.3
9.如图,在△ABC中,∠B=90°,AB=5,BC=12,将△ABC沿DE折叠,使点C落在△ABC边上处,并且,则CD的长是( )
第9题图
A. B. C. D.
10.如图,BD是的对角线,BD⊥AD,AB=2AD=6,点E是CD的中点,点F、P分别是线段AB、BD上的动点,若△ABD∽△PBF,且△PDE是等腰三角形,则PF的长为( )
第10题图
A.或 B.或
C.或 D.或
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果线段a=4cm,b=5mm,那么的值为______.
12.如图,在△ABC中,P为边AB上一点,且∠APC=∠ACB,若AP=4,AC=6,则BP的长为______.
第12题图
13.若正比例函数与反比例函数的图象交于点A(m,1),则k的值是______.
14.已知:如图,在平面直角坐标系xOy中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则抛物线的顶点坐标是______,正方形ABCD周长的最小值是______.
第14题图
三、(本大题共2小题,每小题8分,满分16分)
15.已知,求和值.
16.如图,已知二次函数的图象分别经过点A(2,0),B(0,6),求该函数的解析式.
四、(本大题共2小题,每小题8分,满分16分)
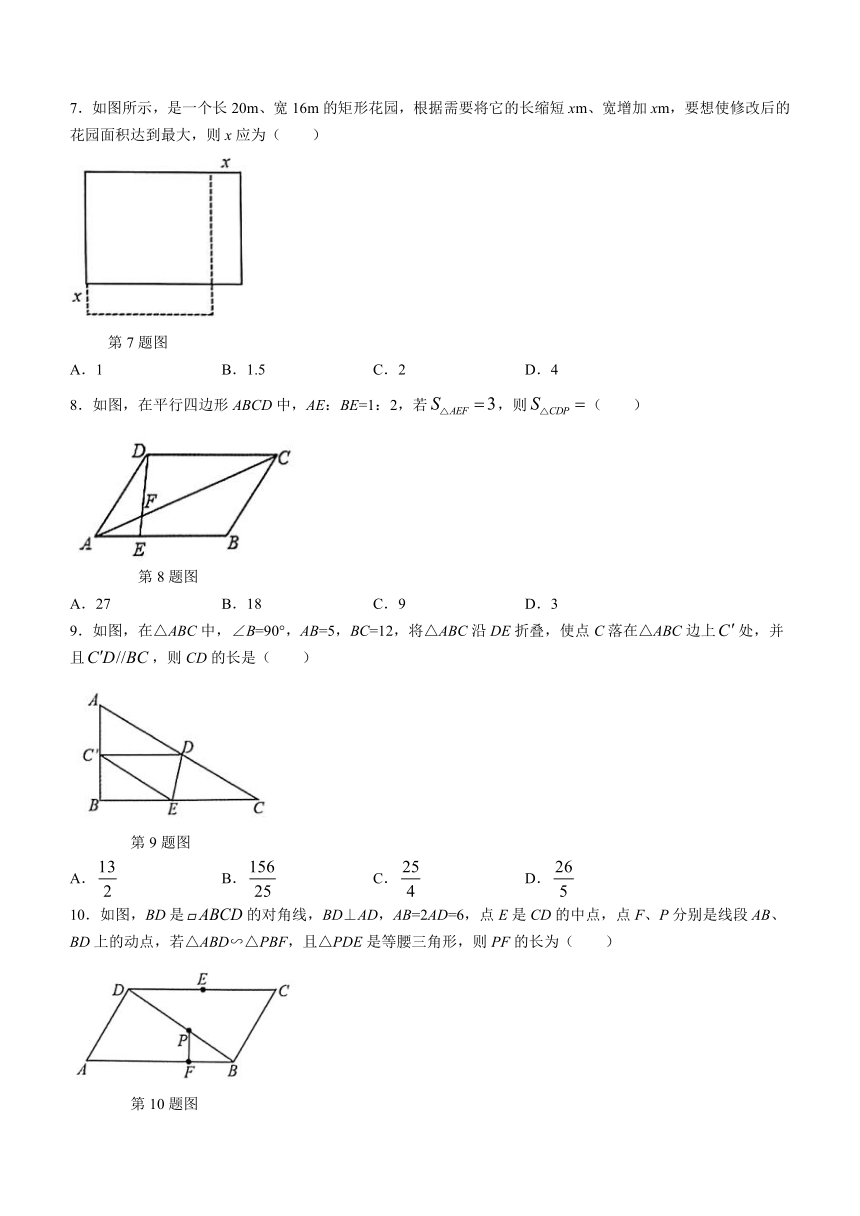
17.如图,在△ABC中,点D是AB上一点,且AD=2,AB=6,,CD=5.求BC的长.
18.如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别为A(6,3),O(0,0),B(0,6).
(1)以原点O为位似中心,在第一象限内将△AOB缩小得到,相似比为,请画出;
(2)直接写出点的坐标(______,______);
(3)求出的面积.
五、(本大题共2小题,每小题10分,总计20分)
19.如图,一次函数A,B是反比例函数图象上的两点,点A的坐标为(2,4),点B的坐标为(4,m),线段AB的延长线交x轴于点C.
(1)求m的值和该反比例函数的函数关系式.
(2)求△AOC的面积.
20.已知:如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过点O的直线,分别交AB、AC于点D、E.
(1)求证:DE=BD+CE;
(2)若AD=4,BD=3,CE=2,求BC的值.
六、(本题满分12分)
21.已知:如图,点D、E分别在△ABC的边AB、AC上,∠ADE=∠B,点F在AD上,且.求证:
(1)ΔDEF∽ΔBCD;
(2).
七、(本题满分12分)
22.某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为m(元),售价每只为n(元),且m、n与x的关系式分别为,.
(1)当日产量为多少时,每日获得的利润为1750元?
(2)当日产量为多少时,可获得最大利润?最大利润是多少?
八、(本题满分14分)
23.如图,四边形ABCD中,BD平分∠ABC,∠ADB=∠DCB=90°,E为AB的中点,CE与BD交于点F,
(1)求证:△ABD∽△DBC;
(2)求证:;
(3)若DF:BF=2:3,CD=6,求DE的长.
2023-2024学年度第一学期九年级阶段性评价参考答案
数学(泸科版)
一、选择题(本大题共10小题,每小题4分,满分40分)
1-5.CBDCA
6-10.DCABC
第10题解析:当PD=PE时,如图①,过点P作PG⊥DE于点G,则.
∵BD是的对角线,BD⊥AD,AB=2AD=6,
∴△ABD是直角三角形.∠PDG=∠ABP=30°,,PD=2PG.
∴,,
又∵△ABD∽APBF,∴∠PFB=∠ADB=90°,∴;
当DE=DP=3时,如图②,,∴,
当ED=EP=3时,点P与点B重合,不存在△BPF.
综上所述,PF的长为或.
图① 图②
二、填空题(本大题共4小题,每小题5分,满分20分)
11.8
12.5.
13.
14.(4,2),
14.解:∵,∴抛物线的顶点坐标为(4,2);
∵四边形ABCD是正方形,∴,
∵点A在抛物线上运动,∴当x=4时,AC有最小值2,
即AB的最小值是,正方形ABCD周长的最小值为.
三、(本大题共2小题,每小题8分,满分16分)
15.解:∵,∴a=6b,c=6d.
∴,.8分
16.解:∵二次函数过点A(2,0),B(0,6),
∴,解得,
∴二次函数的解析式为.8分
四、(本大题共2小题,每小题8分,满分16分)
17.证明:∵AD=2,AB=6,,CD=5
∴,,∴
又∵∠A=∠A,∴△ACD∽△ABC.5分
∴,即
∴.8分
18.解:(1)如图,即为所求;2分
(2)点的坐标为.5分
(3)
答:的面积为.8分
五、(本大题共2小题,每小题10分,满分20分)
19.解:(1)把A(2,4)代入得,解得k=8.
把B(4,m)代入得,解得m=2;
∴m=2,该反比例函数的函数关系式为.5分
(2)设直线AB的函数关系式为,把A(2,4),B(4,2)分別代入得,
解得,∴直线AB的函数关系式为,
当y=0时,x=6,即点C的坐标为(6,0)
∴,即△AOC的面积为12.10分
20.解:(1)证明:∵在△ABC中,OB和OC分别平分∠ABC和∠ACB,∴∠DBO=∠OBC,∠ECO=∠OCB,
又∵,∴∠DOB=∠OBC=∠DBO,∠EOC=∠OCB=∠ECO,
∴DB=DO,OE=EC,
∵DE=DO+OE,
∴DE=BD+EC;5分
(2)∵AD=4,BD=3,CE=2
∴DE=BD+EC=5,AB=AD+BD=7
∵,∴ΔADE∽ΔABC,
∴,即,∴.10分
六、(本题满分12分)
21.证明:(1)∵∠ADE=∠B,
∴,∴∠CDE=∠BCD,
∵,∴∠CDE=∠DEF,∴∠BCD=∠DEF,
又∵∠ADE=∠B,
∴△DEF∽△BCD.6分
(2)∵∠ADE=∠B,∴,∴,
∵,∴,∴,
∴.12分
七、(本题满分12分)
22.解:(1)由题意得:,
解得,
又∵x≤40,∴x=25
答:当日产量为25只时,每日获得的利润为1750元.6分
(2)设每天所获利润为w元,
由题意得,.
答:当日产量为35只时,可获得最大利润,最大利润是1950元.12分
八、(本题满分14分)
23.解:(1)证明:∵BD平分∠ABC,
∴∠CBD=∠ABD.
又∵∠ADB=∠DCB,
∴△ABD∽△DBC.3分
证明:∵点E是AB的中点,∠ADB=90°,
∴DE=BE=AE,
∴∠EDB=∠ABD.
又∵∠CBD=∠ABD,
∴∠CBD=∠EDB.
∴.8分
(3)解法一:过点D作DH⊥AB
易证△DHB≌△DCB
∴ΔDEF∽ΔBCF,∴,
设DE=2k,BC=3k,则BH=3k.
DE=BE=2k,HE=k.
∵BD平分∠ABC
∴DH=CD=6
在Rt△DHE中,
.
解法二:
∵
∴ΔDEF∽ΔBCF
∴
又∵DF:BF=2:3
∴
设DE=2k,则BC=3k.
∵E是AB的中点,∠ADB=90°.
∴AB=2DE=4k
∵ΔABD∽ΔDBC
∴
∴
∵∠BCD=90°,CD=6
∴,即
解得
∴.
数学(泸科版)
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分)
1.已知线段a=4,b=6,如果线段b是线段a和c的比例中项那么线段c的长度是( )
A. B.8 C.9 D.10
2.若抛物线经过A(-2,6),B(8,6)两点,则抛物线的对称轴为( )
A.直线 B.直线 C.直线 D.直线
3.对于抛物线的说法正确的是( )
A.开口向上 B.顶点坐标是(1,-2)
C.对称轴是直线x=1 D.当x<-1时,y随x的增大而增大
4.已知两个相似三角形的相似比为2:3,则它们的周长的比为( )
A.4:9 B.3:2 C.2:3 D.4:6
5.已知某抛物线与二次函数的图象的开口大小相同,开口方向相反,且顶点坐标为(1,2023),则该抛物线对应的函数表达式为( )
A. B.
C. D.
6.如图,已知D、E分别在△ABC的AB、AC边上,△ABC∽△AED,则下列各式成立的是( )
第6题图
A. B.
C. D..
7.如图所示,是一个长20m、宽16m的矩形花园,根据需要将它的长缩短xm、宽增加xm,要想使修改后的花园面积达到最大,则x应为( )
第7题图
A.1 B.1.5 C.2 D.4
8.如图,在平行四边形ABCD中,AE:BE=1:2,若,则( )
第8题图
A.27 B.18 C.9 D.3
9.如图,在△ABC中,∠B=90°,AB=5,BC=12,将△ABC沿DE折叠,使点C落在△ABC边上处,并且,则CD的长是( )
第9题图
A. B. C. D.
10.如图,BD是的对角线,BD⊥AD,AB=2AD=6,点E是CD的中点,点F、P分别是线段AB、BD上的动点,若△ABD∽△PBF,且△PDE是等腰三角形,则PF的长为( )
第10题图
A.或 B.或
C.或 D.或
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果线段a=4cm,b=5mm,那么的值为______.
12.如图,在△ABC中,P为边AB上一点,且∠APC=∠ACB,若AP=4,AC=6,则BP的长为______.
第12题图
13.若正比例函数与反比例函数的图象交于点A(m,1),则k的值是______.
14.已知:如图,在平面直角坐标系xOy中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则抛物线的顶点坐标是______,正方形ABCD周长的最小值是______.
第14题图
三、(本大题共2小题,每小题8分,满分16分)
15.已知,求和值.
16.如图,已知二次函数的图象分别经过点A(2,0),B(0,6),求该函数的解析式.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在△ABC中,点D是AB上一点,且AD=2,AB=6,,CD=5.求BC的长.
18.如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别为A(6,3),O(0,0),B(0,6).
(1)以原点O为位似中心,在第一象限内将△AOB缩小得到,相似比为,请画出;
(2)直接写出点的坐标(______,______);
(3)求出的面积.
五、(本大题共2小题,每小题10分,总计20分)
19.如图,一次函数A,B是反比例函数图象上的两点,点A的坐标为(2,4),点B的坐标为(4,m),线段AB的延长线交x轴于点C.
(1)求m的值和该反比例函数的函数关系式.
(2)求△AOC的面积.
20.已知:如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过点O的直线,分别交AB、AC于点D、E.
(1)求证:DE=BD+CE;
(2)若AD=4,BD=3,CE=2,求BC的值.
六、(本题满分12分)
21.已知:如图,点D、E分别在△ABC的边AB、AC上,∠ADE=∠B,点F在AD上,且.求证:
(1)ΔDEF∽ΔBCD;
(2).
七、(本题满分12分)
22.某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为m(元),售价每只为n(元),且m、n与x的关系式分别为,.
(1)当日产量为多少时,每日获得的利润为1750元?
(2)当日产量为多少时,可获得最大利润?最大利润是多少?
八、(本题满分14分)
23.如图,四边形ABCD中,BD平分∠ABC,∠ADB=∠DCB=90°,E为AB的中点,CE与BD交于点F,
(1)求证:△ABD∽△DBC;
(2)求证:;
(3)若DF:BF=2:3,CD=6,求DE的长.
2023-2024学年度第一学期九年级阶段性评价参考答案
数学(泸科版)
一、选择题(本大题共10小题,每小题4分,满分40分)
1-5.CBDCA
6-10.DCABC
第10题解析:当PD=PE时,如图①,过点P作PG⊥DE于点G,则.
∵BD是的对角线,BD⊥AD,AB=2AD=6,
∴△ABD是直角三角形.∠PDG=∠ABP=30°,,PD=2PG.
∴,,
又∵△ABD∽APBF,∴∠PFB=∠ADB=90°,∴;
当DE=DP=3时,如图②,,∴,
当ED=EP=3时,点P与点B重合,不存在△BPF.
综上所述,PF的长为或.
图① 图②
二、填空题(本大题共4小题,每小题5分,满分20分)
11.8
12.5.
13.
14.(4,2),
14.解:∵,∴抛物线的顶点坐标为(4,2);
∵四边形ABCD是正方形,∴,
∵点A在抛物线上运动,∴当x=4时,AC有最小值2,
即AB的最小值是,正方形ABCD周长的最小值为.
三、(本大题共2小题,每小题8分,满分16分)
15.解:∵,∴a=6b,c=6d.
∴,.8分
16.解:∵二次函数过点A(2,0),B(0,6),
∴,解得,
∴二次函数的解析式为.8分
四、(本大题共2小题,每小题8分,满分16分)
17.证明:∵AD=2,AB=6,,CD=5
∴,,∴
又∵∠A=∠A,∴△ACD∽△ABC.5分
∴,即
∴.8分
18.解:(1)如图,即为所求;2分
(2)点的坐标为.5分
(3)
答:的面积为.8分
五、(本大题共2小题,每小题10分,满分20分)
19.解:(1)把A(2,4)代入得,解得k=8.
把B(4,m)代入得,解得m=2;
∴m=2,该反比例函数的函数关系式为.5分
(2)设直线AB的函数关系式为,把A(2,4),B(4,2)分別代入得,
解得,∴直线AB的函数关系式为,
当y=0时,x=6,即点C的坐标为(6,0)
∴,即△AOC的面积为12.10分
20.解:(1)证明:∵在△ABC中,OB和OC分别平分∠ABC和∠ACB,∴∠DBO=∠OBC,∠ECO=∠OCB,
又∵,∴∠DOB=∠OBC=∠DBO,∠EOC=∠OCB=∠ECO,
∴DB=DO,OE=EC,
∵DE=DO+OE,
∴DE=BD+EC;5分
(2)∵AD=4,BD=3,CE=2
∴DE=BD+EC=5,AB=AD+BD=7
∵,∴ΔADE∽ΔABC,
∴,即,∴.10分
六、(本题满分12分)
21.证明:(1)∵∠ADE=∠B,
∴,∴∠CDE=∠BCD,
∵,∴∠CDE=∠DEF,∴∠BCD=∠DEF,
又∵∠ADE=∠B,
∴△DEF∽△BCD.6分
(2)∵∠ADE=∠B,∴,∴,
∵,∴,∴,
∴.12分
七、(本题满分12分)
22.解:(1)由题意得:,
解得,
又∵x≤40,∴x=25
答:当日产量为25只时,每日获得的利润为1750元.6分
(2)设每天所获利润为w元,
由题意得,.
答:当日产量为35只时,可获得最大利润,最大利润是1950元.12分
八、(本题满分14分)
23.解:(1)证明:∵BD平分∠ABC,
∴∠CBD=∠ABD.
又∵∠ADB=∠DCB,
∴△ABD∽△DBC.3分
证明:∵点E是AB的中点,∠ADB=90°,
∴DE=BE=AE,
∴∠EDB=∠ABD.
又∵∠CBD=∠ABD,
∴∠CBD=∠EDB.
∴.8分
(3)解法一:过点D作DH⊥AB
易证△DHB≌△DCB
∴ΔDEF∽ΔBCF,∴,
设DE=2k,BC=3k,则BH=3k.
DE=BE=2k,HE=k.
∵BD平分∠ABC
∴DH=CD=6
在Rt△DHE中,
.
解法二:
∵
∴ΔDEF∽ΔBCF
∴
又∵DF:BF=2:3
∴
设DE=2k,则BC=3k.
∵E是AB的中点,∠ADB=90°.
∴AB=2DE=4k
∵ΔABD∽ΔDBC
∴
∴
∵∠BCD=90°,CD=6
∴,即
解得
∴.
同课章节目录
