江苏省徐州市2023-2024学年上学期八年级数学期中模拟卷(无答案)
文档属性
| 名称 | 江苏省徐州市2023-2024学年上学期八年级数学期中模拟卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 346.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 10:21:48 | ||
图片预览


文档简介
徐州市2023-2024学年度八年级数学期中模拟卷3
一、单选题
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是
A. B. C. D.
2. 下列各组数中,是勾股数的是( )
A.6,9,12 B.2,3,4 C.5,12,13 D.,,
3.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果a2=b2﹣c2,那么△ABC是直角三角形且∠B=90°
B.如果,那么△ABC是直角三角形
C.如果∠A:∠B:∠C=3:4:5,那么△ABC是直角三角形
D.如果∠A﹣∠B=∠C,那么△ABC是直角三角形
4.下列各组数中,不是勾股数的是( )
A.3,4,5 B.5,12,13 C.8,15,17 D.6,7,9
5.如图,在平面直角坐标系中,点P坐标为(﹣4,6),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.﹣8和﹣7之间 B.7和8之间 C.9和﹣8之间 D.8和9之间
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=3,则△BCE的面积等于( )
A.6 B.8 C.9 D.18
7.如图,将折叠,使边落在边上,展开后得到折痕与交于点,且点到的距离为,点为上任意一点,则的最小值为
A. B. C. D.
8.如图,在边长为6的正方形内作交于点E,交于点F,连接.若,则的长为( )
A.2 B.3 C.4 D.5
9.如图,点P是∠AOB的角平分线OC上一点,PE⊥OA,OE=10,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4,则△PGE的面积为( )
A.5 B.10 C.20 D.40
10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,
如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,小正方形的面积为5,则大正方形的面积为( )
A.12 B.13 C.14 D.15
二、填空题
1.等腰三角形的一个外角为,那么它的一个底角为 .
2. 已知,将的数值精确到0.01为__ .
3. 如图,在中,,,,以为边构造如图所示的等边,连接,则的长为_ _ .
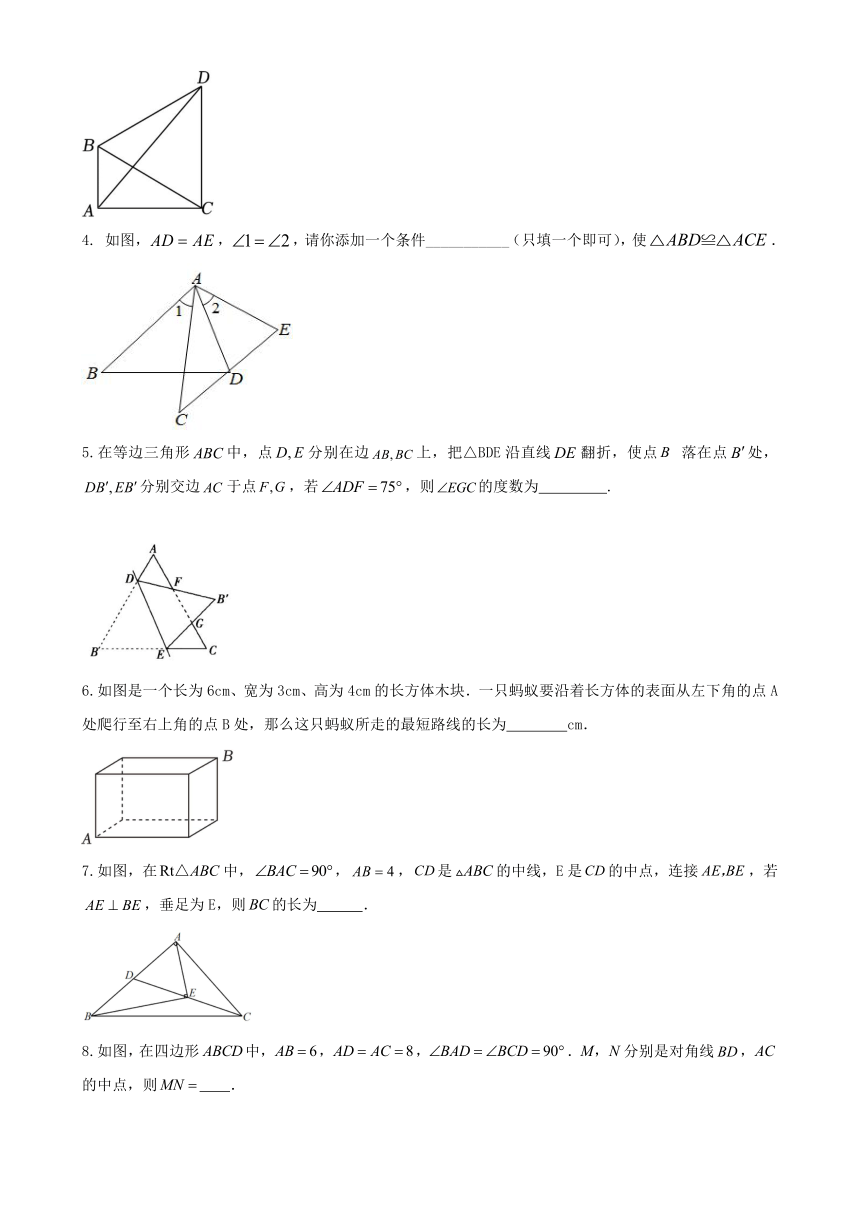
4. 如图,,,请你添加一个条件___________(只填一个即可),使.
5.在等边三角形中,点分别在边上,把△BDE沿直线翻折,使点 落在点处, 分别交边于点,若,则的度数为 .
6.如图是一个长为6cm、宽为3cm、高为4cm的长方体木块.一只蚂蚁要沿着长方体的表面从左下角的点A处爬行至右上角的点B处,那么这只蚂蚁所走的最短路线的长为 cm.
7.如图,在中,,,是的中线,E是的中点,连接,若,垂足为E,则的长为 .
8.如图,在四边形中,,,.分别是对角线,的中点,则 .
三、解答题
1.求下列各式中的值:
(1); (2).
2.如图,在和中,,,,与交于点,与交于点.
(1)求证:;
(2)若,求的度数.
3.如图,在中,O为,的平分线的交点,,,,垂足分别为.
(1)与是否相等,请说明理由;
(2)若的周长是30,且,求的面积.
4.如图,海中有一小岛,它的周围12海里内有暗礁,渔船跟踪鱼群由西向东航行,在处测得小岛在北偏东方向上,航行16海里到处,这时测得小岛在北偏东方向上.
(1)求点与小岛的距离;
(2)如果渔船不改变航线继续向东航行,是否有触礁危险,并说明理由.
5.如图,两条公路,相交于点C,从A点沿直线再修建一条公路到B点.若,,.
(1)求证:
(2)若公路的中点M与点C被湖隔开.求M,C两点间的距离.
6. 如图所示,在等腰ABC中,AB=AC,AF为BC的中线,D为AF上的一点,且BD的垂直平分线过点C并交BD于E,求证:BCD是等边三角形.
7. 【阅读材料】我们知道是无理数,而无理数是无限不循环小数,它小数部分我们不可能全部地写出来,但是由于1<<2,所以的整数部分为1,减去其整数部分,差就是的小数部分,所以用-1来表示的小数部分.
根据以上内容,解答下面的问题:
(1)填空:的整数部分是,的小数部分是.
(2)若-2=m+n,其中是m整数,且08.已知△ABC中,AC=BC;△DEC中,DC=EC;∠ACB=∠DCE=α,
(1)如图1,当α=60°时,①求证:AD=BE;②求出∠AEB的度数;
(2)如图2,当α=90°时,求:
①∠AEB的度数;②若∠CAF=∠BAF,BE=2,求AF的长.
一、单选题
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是
A. B. C. D.
2. 下列各组数中,是勾股数的是( )
A.6,9,12 B.2,3,4 C.5,12,13 D.,,
3.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果a2=b2﹣c2,那么△ABC是直角三角形且∠B=90°
B.如果,那么△ABC是直角三角形
C.如果∠A:∠B:∠C=3:4:5,那么△ABC是直角三角形
D.如果∠A﹣∠B=∠C,那么△ABC是直角三角形
4.下列各组数中,不是勾股数的是( )
A.3,4,5 B.5,12,13 C.8,15,17 D.6,7,9
5.如图,在平面直角坐标系中,点P坐标为(﹣4,6),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
A.﹣8和﹣7之间 B.7和8之间 C.9和﹣8之间 D.8和9之间
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=3,则△BCE的面积等于( )
A.6 B.8 C.9 D.18
7.如图,将折叠,使边落在边上,展开后得到折痕与交于点,且点到的距离为,点为上任意一点,则的最小值为
A. B. C. D.
8.如图,在边长为6的正方形内作交于点E,交于点F,连接.若,则的长为( )
A.2 B.3 C.4 D.5
9.如图,点P是∠AOB的角平分线OC上一点,PE⊥OA,OE=10,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4,则△PGE的面积为( )
A.5 B.10 C.20 D.40
10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,
如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,小正方形的面积为5,则大正方形的面积为( )
A.12 B.13 C.14 D.15
二、填空题
1.等腰三角形的一个外角为,那么它的一个底角为 .
2. 已知,将的数值精确到0.01为__ .
3. 如图,在中,,,,以为边构造如图所示的等边,连接,则的长为_ _ .
4. 如图,,,请你添加一个条件___________(只填一个即可),使.
5.在等边三角形中,点分别在边上,把△BDE沿直线翻折,使点 落在点处, 分别交边于点,若,则的度数为 .
6.如图是一个长为6cm、宽为3cm、高为4cm的长方体木块.一只蚂蚁要沿着长方体的表面从左下角的点A处爬行至右上角的点B处,那么这只蚂蚁所走的最短路线的长为 cm.
7.如图,在中,,,是的中线,E是的中点,连接,若,垂足为E,则的长为 .
8.如图,在四边形中,,,.分别是对角线,的中点,则 .
三、解答题
1.求下列各式中的值:
(1); (2).
2.如图,在和中,,,,与交于点,与交于点.
(1)求证:;
(2)若,求的度数.
3.如图,在中,O为,的平分线的交点,,,,垂足分别为.
(1)与是否相等,请说明理由;
(2)若的周长是30,且,求的面积.
4.如图,海中有一小岛,它的周围12海里内有暗礁,渔船跟踪鱼群由西向东航行,在处测得小岛在北偏东方向上,航行16海里到处,这时测得小岛在北偏东方向上.
(1)求点与小岛的距离;
(2)如果渔船不改变航线继续向东航行,是否有触礁危险,并说明理由.
5.如图,两条公路,相交于点C,从A点沿直线再修建一条公路到B点.若,,.
(1)求证:
(2)若公路的中点M与点C被湖隔开.求M,C两点间的距离.
6. 如图所示,在等腰ABC中,AB=AC,AF为BC的中线,D为AF上的一点,且BD的垂直平分线过点C并交BD于E,求证:BCD是等边三角形.
7. 【阅读材料】我们知道是无理数,而无理数是无限不循环小数,它小数部分我们不可能全部地写出来,但是由于1<<2,所以的整数部分为1,减去其整数部分,差就是的小数部分,所以用-1来表示的小数部分.
根据以上内容,解答下面的问题:
(1)填空:的整数部分是,的小数部分是.
(2)若-2=m+n,其中是m整数,且0
(1)如图1,当α=60°时,①求证:AD=BE;②求出∠AEB的度数;
(2)如图2,当α=90°时,求:
①∠AEB的度数;②若∠CAF=∠BAF,BE=2,求AF的长.
同课章节目录
