数学人教A版(2019)必修第一册5.1.1任意角(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.1任意角(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 13:12:27 | ||
图片预览





文档简介
(共24张PPT)
5.1任意角和弧度制
5.1.1 任意角
引入
现实世界中的许多运动变化都有循环往复,周而复始的规律,这种变化规律叫周期性。例如:
地球自转引起的昼夜交替变化,地球公转引起的四季交替变化,月亮的圆缺,潮汐的涨落,做匀速圆周运动时物体位置的变化,做简谐运动时物体位移的变化,交变电流的变化 。
这些现象都可以用三角函数来刻画。
前面我们学习了一般函数,并研究了幂、指、对函数,知道了函数的研究内容、过程和方法,以及如何用某类函数刻画相应现实问题的变化规律。本章将利用这些经验,学习刻画周期性变化规律的三角函数。
本章将主要研究以下问题:三角函数是怎样的函数?它具有哪一些性质?如何利用三角函数刻画各种周期性变化现象?
思考: 角是平面几何中的一个基本图形。回顾我们以前学过的相关知识,你能说一说什么是角吗?角的取值范围又是怎样的呢?
(1)有公共端点的两射线组成的几何图形叫角.
(顶点)
(边)
(边)
角的范围:
静态定义
角是“夹”出来的
(2)一条射线绕着它端点从一个位置旋转到另一个位置所成的图形叫做角.
始边
终边
旋转方向
角是“转”出来的
动态定义
0°~360°
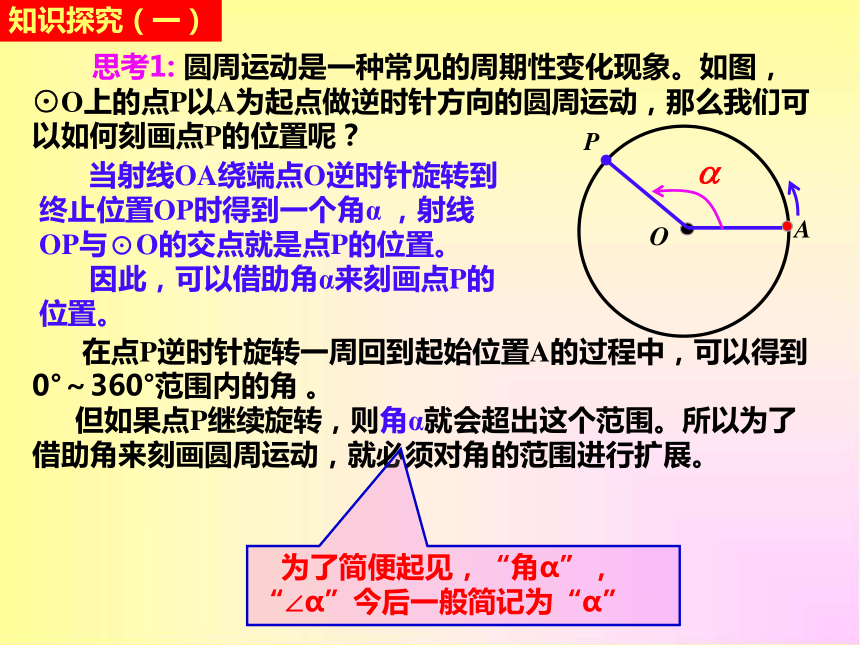
思考1: 圆周运动是一种常见的周期性变化现象。如图,⊙O上的点P以A为起点做逆时针方向的圆周运动,那么我们可以如何刻画点P的位置呢?
当射线OA绕端点O逆时针旋转到终止位置OP时得到一个角α ,射线OP与⊙O的交点就是点P的位置。
因此,可以借助角α来刻画点P的位置。
在点P逆时针旋转一周回到起始位置A的过程中,可以得到0°~360°范围内的角 。
但如果点P继续旋转,则角α就会超出这个范围。所以为了借助角来刻画圆周运动,就必须对角的范围进行扩展。
为了简便起见,“角α”,“∠α”今后一般简记为“α”
知识探究(一)
思考2::事实上,现实生活中到处是超出0°~360°范围的角,例如
(1)在体操常有“前空翻转体540°”、“后空翻转体720°”这样的动作名称,这两个角不仅范围超出,而且旋转的方向也不相同;
(2)在齿轮传动中,被动轮随着主动轮的旋转而旋转,而且被动轮与主动轮的旋转方向是相反的。即射线OA旋转形成的角与射线O′B旋转形成的角方向是不一样的。
由此,你认为角的概念应怎样进行推广?
在角的定义中,由于射线的旋转中心是固定的(射线的端点),因此,为了准确描述这些旋转现象,还应知道旋转量,以及旋转的方向。
所以,角的扩展应包含两个方面:
一是射线旋转的度数不能只限于0°~360°的范围
二是射线的不同旋转方向所形成的角要有所区别。
旋转三要素:旋转中心,
旋转量,
旋转方向
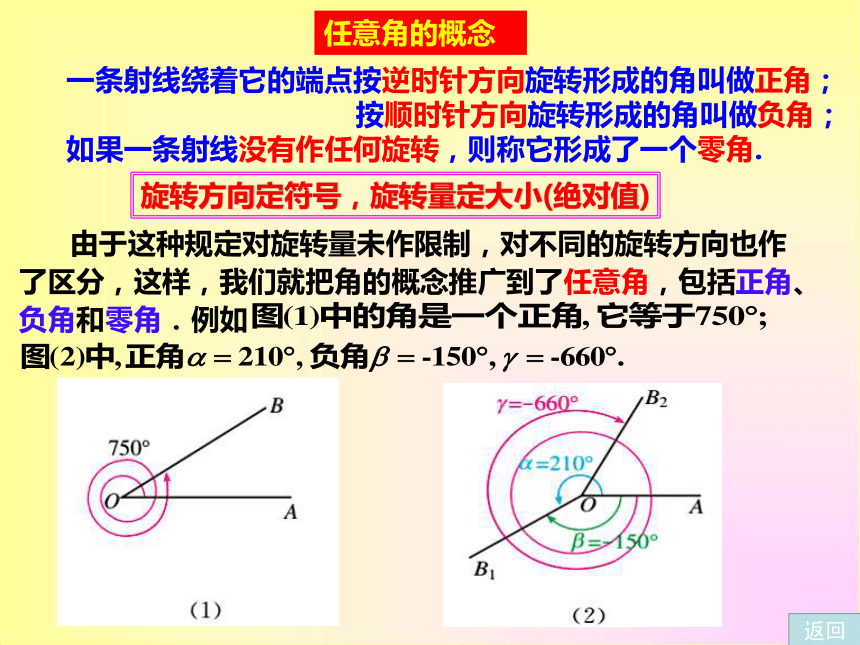
一条射线绕着它的端点按逆时针方向旋转形成的角叫做正角;
按顺时针方向旋转形成的角叫做负角;
如果一条射线没有作任何旋转,则称它形成了一个零角.
任意角的概念
由于这种规定对旋转量未作限制,对不同的旋转方向也作了区分,这样,我们就把角的概念推广到了任意角,包括正角、负角和零角.例如
旋转方向定符号,旋转量定大小(绝对值)
返回
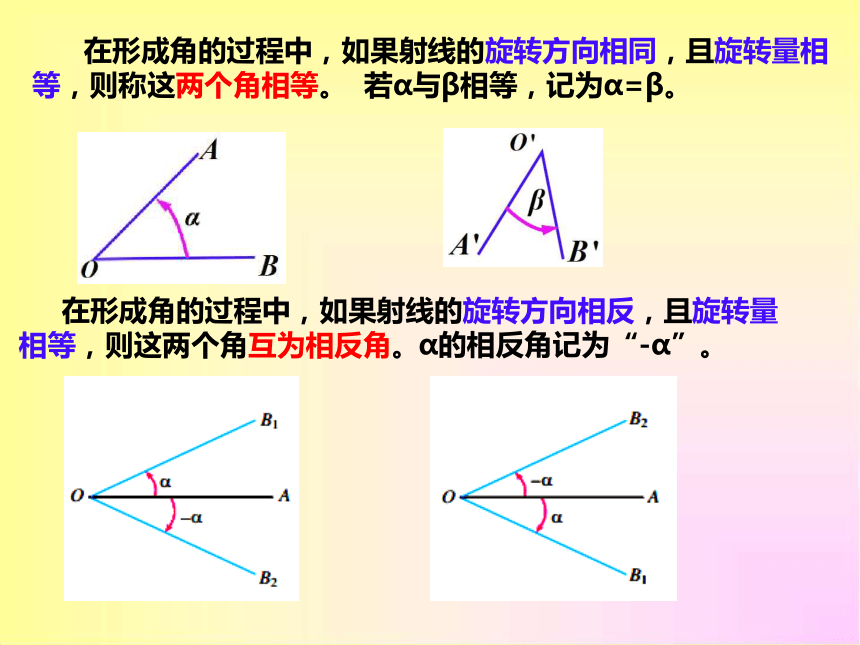
在形成角的过程中,如果射线的旋转方向相同,且旋转量相等,则称这两个角相等。
在形成角的过程中,如果射线的旋转方向相反,且旋转量相等,则这两个角互为相反角。
若α与β相等,记为α=β。
α的相反角记为“-α”。
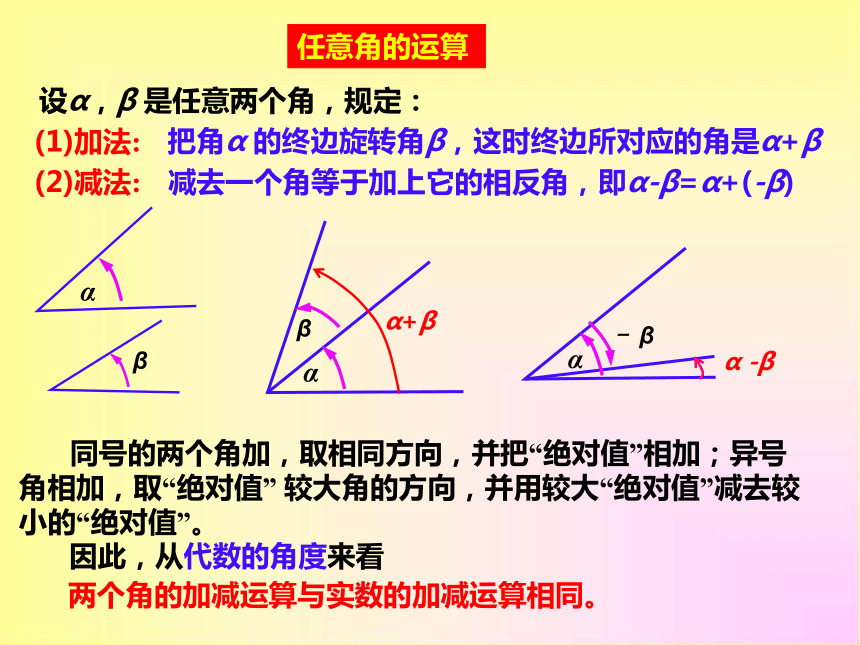
设α,β 是任意两个角,规定:
减去一个角等于加上它的相反角,即α-β=α+(-β)
α
- β
α -β
α
β
α
α+β
β
两个角的加减运算与实数的加减运算相同。
同号的两个角加,取相同方向,并把“绝对值”相加;异号角相加,取“绝对值” 较大角的方向,并用较大“绝对值”减去较小的“绝对值”。
因此,从代数的角度来看
任意角的运算
(1)加法:
(2)减法:
把角α 的终边旋转角β,这时终边所对应的角是α+β
1.请说说50°+80°=130°,50°-80°=-30°的几何意义吗?
50°+80°=130°:
将射线绕着端点先逆时针旋转50°后,再逆时针旋转80°就形成130°角.
或以50°角的终边为始边,逆时针旋转80°,则以50°角的始边为始边,逆时针旋转80°后的终边为终边所成的角就是130°角.
50°-80°=-30°:
将射线绕着端点先逆时针旋转50°后,再顺时针旋转80°就形成-30°角.
或以50°角的终边为始边,顺时针旋转80°,则以50°角的始边为始边,顺时针旋转80°后的终边为终边所成的角就是-30°角.
练习
2.若90 <α<β<135 ,则α-β的范围是_______________,
α+β的范围是________________.
(-45 , 0 )
(180 , 270 )
知识探究(二)
思考1:为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,角的终边可能在哪些位置?
把角放在直角坐标系中,使:
(1)角的顶点与坐标原点重合;
(2)角的始边与x轴的非负半轴重合. 则
角的终边在第几象限,我们就说这个角是第几象限角.
角的终边在坐标轴限,我们就说这个角不属于任何象限,习惯上称为轴线角。
终边可能落在某个象限内,也可能落在坐标轴上。
象限角和轴线角
第一象限角
第二象限角
第三象限角
第四象限角
返回
练习
1.已知角的顶点与原点重合, 角的始边与x轴的非负半轴重合, 请作出下列各角,并指出它们各是哪个象限的角?
(1)420 , (2)-75 , (3)855 , (4) -510 .(教材P171第3题)
第一象限角
420
-75
第四象限角
855
第二象限角
-510
第三象限角
2.经过3小时15分,时钟的分针和时针旋转所形成的角各是多少,它们各是几象限角?
解:
解:
分针旋转所形成的角是-1170 ,
它是第四象限角;
时针针旋转所形成的角是
它是第三象限角.
-97.5 ,
思考2:将角按照上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线,以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
328°
-392°
设射线OB是-32°的终边,则
-392°,... , 328°,...的终边也是OB,
这些角与-32°相差360°的整数倍。即
这些角可以表示为
-32°+k·360°(k∈Z)
如328°=-32°+360°(这里k=_____)
328°=-32°-360° (这里k=_____)
1
-1
思考4:由以上你能得出什么结论?
与角α的终边相同的角有无数多个,它们之差相差360 的整数倍。这些角(含α本身)可以表示为都可以用α+k·360(k∈Z)来表示。
思考3:-32°本身能用这种形式表示吗?
-328-°=-32°-0×360° (这里k=0)
{β|β=α+k·360°,k∈Z},
一般地,所有与角α终边相同的角,连同角α在内所构成的集合可表示为:
终边相同角的表示
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
注意:
(1)k∈Z。
“ K > 0”表示β是将α的终边逆时针旋转得到的;
“K < 0”表示β是将α的终边顺时针旋转得到的;
“K = 0”表示β就是α本身。
(2)α是任意角;
(3)终边相同的角不一定相相等,它们有无数多个,它们之间差相差360 的整数倍
返回
例析
思考:通过本题,你能说说如何在给定的范围内求出与已知角α终边相同的角吗?
第1步:
写出与已知角α终边相同的角:α+k·360°,k∈Z,
第2步:
让k取适当的整数,让角α+k·360°落在给定的范围内。
练习
(教材P171练习第4题)
(教材P171练习第4题)
例析
返回
思考:利用本题的方法(先在0°~360°内找出该角,再时上360°的整数倍),你能说说各象限角所组成的集合各是怎样的吗?
返回
练习
2.今天是星期三, 则7k(k∈Z)天后的那一天是星期几 7k(k∈Z)
天前的那一天是星期几 100天后的那一天是星期几
7k(k∈Z)天后和7k天前的那一天都是星期三
∵100=14×7+2
∴100天后的那一天是星期五
1.什么是锐角 它是几象限角,反过来成立吗
钝角呢?直角呢?
角的概念
1. 请说说角的概念是怎样扩展的?
小结
3.如何将角放在平面直角坐标系中?什么是象限角,轴线角?
(0°~360°)
不限制旋转量
对不同旋转方向作出区分
(任意角)
2.任意角怎样进行加减运算?其几何意义是怎样的?
0°~360°的角不够用
放在坐标系中
看终边的位置
如何表示象限角,轴线角?
4.与α终边相现的角如何表示?如何在给定的范围找出与已知角终边相同的角?
α+k·360°,k∈Z
先写出与已知角α终边相同的角:α+k·360°,k∈Z,
再让k取适当的整数,让角α+k·360°落在给定的范围内。
作业
1.教材P175习题5.1第1, 2(3)(4)(7)(8)题
2.写出终边在阴影部分中的角的集合:
(1)
(2)
3.(选做题)试完成下表:
α,2α, 的终边所在的位置
α 一象限 二象限 三象限 四象限
2α
一、三象限前半区
一、三象限后半区
二、四象限前半区
二、四象限后半区
x轴上半区
x轴上半区
x轴下半区
x轴下半区
2.
(1)
(2)
再 见
5.1任意角和弧度制
5.1.1 任意角
引入
现实世界中的许多运动变化都有循环往复,周而复始的规律,这种变化规律叫周期性。例如:
地球自转引起的昼夜交替变化,地球公转引起的四季交替变化,月亮的圆缺,潮汐的涨落,做匀速圆周运动时物体位置的变化,做简谐运动时物体位移的变化,交变电流的变化 。
这些现象都可以用三角函数来刻画。
前面我们学习了一般函数,并研究了幂、指、对函数,知道了函数的研究内容、过程和方法,以及如何用某类函数刻画相应现实问题的变化规律。本章将利用这些经验,学习刻画周期性变化规律的三角函数。
本章将主要研究以下问题:三角函数是怎样的函数?它具有哪一些性质?如何利用三角函数刻画各种周期性变化现象?
思考: 角是平面几何中的一个基本图形。回顾我们以前学过的相关知识,你能说一说什么是角吗?角的取值范围又是怎样的呢?
(1)有公共端点的两射线组成的几何图形叫角.
(顶点)
(边)
(边)
角的范围:
静态定义
角是“夹”出来的
(2)一条射线绕着它端点从一个位置旋转到另一个位置所成的图形叫做角.
始边
终边
旋转方向
角是“转”出来的
动态定义
0°~360°
思考1: 圆周运动是一种常见的周期性变化现象。如图,⊙O上的点P以A为起点做逆时针方向的圆周运动,那么我们可以如何刻画点P的位置呢?
当射线OA绕端点O逆时针旋转到终止位置OP时得到一个角α ,射线OP与⊙O的交点就是点P的位置。
因此,可以借助角α来刻画点P的位置。
在点P逆时针旋转一周回到起始位置A的过程中,可以得到0°~360°范围内的角 。
但如果点P继续旋转,则角α就会超出这个范围。所以为了借助角来刻画圆周运动,就必须对角的范围进行扩展。
为了简便起见,“角α”,“∠α”今后一般简记为“α”
知识探究(一)
思考2::事实上,现实生活中到处是超出0°~360°范围的角,例如
(1)在体操常有“前空翻转体540°”、“后空翻转体720°”这样的动作名称,这两个角不仅范围超出,而且旋转的方向也不相同;
(2)在齿轮传动中,被动轮随着主动轮的旋转而旋转,而且被动轮与主动轮的旋转方向是相反的。即射线OA旋转形成的角与射线O′B旋转形成的角方向是不一样的。
由此,你认为角的概念应怎样进行推广?
在角的定义中,由于射线的旋转中心是固定的(射线的端点),因此,为了准确描述这些旋转现象,还应知道旋转量,以及旋转的方向。
所以,角的扩展应包含两个方面:
一是射线旋转的度数不能只限于0°~360°的范围
二是射线的不同旋转方向所形成的角要有所区别。
旋转三要素:旋转中心,
旋转量,
旋转方向
一条射线绕着它的端点按逆时针方向旋转形成的角叫做正角;
按顺时针方向旋转形成的角叫做负角;
如果一条射线没有作任何旋转,则称它形成了一个零角.
任意角的概念
由于这种规定对旋转量未作限制,对不同的旋转方向也作了区分,这样,我们就把角的概念推广到了任意角,包括正角、负角和零角.例如
旋转方向定符号,旋转量定大小(绝对值)
返回
在形成角的过程中,如果射线的旋转方向相同,且旋转量相等,则称这两个角相等。
在形成角的过程中,如果射线的旋转方向相反,且旋转量相等,则这两个角互为相反角。
若α与β相等,记为α=β。
α的相反角记为“-α”。
设α,β 是任意两个角,规定:
减去一个角等于加上它的相反角,即α-β=α+(-β)
α
- β
α -β
α
β
α
α+β
β
两个角的加减运算与实数的加减运算相同。
同号的两个角加,取相同方向,并把“绝对值”相加;异号角相加,取“绝对值” 较大角的方向,并用较大“绝对值”减去较小的“绝对值”。
因此,从代数的角度来看
任意角的运算
(1)加法:
(2)减法:
把角α 的终边旋转角β,这时终边所对应的角是α+β
1.请说说50°+80°=130°,50°-80°=-30°的几何意义吗?
50°+80°=130°:
将射线绕着端点先逆时针旋转50°后,再逆时针旋转80°就形成130°角.
或以50°角的终边为始边,逆时针旋转80°,则以50°角的始边为始边,逆时针旋转80°后的终边为终边所成的角就是130°角.
50°-80°=-30°:
将射线绕着端点先逆时针旋转50°后,再顺时针旋转80°就形成-30°角.
或以50°角的终边为始边,顺时针旋转80°,则以50°角的始边为始边,顺时针旋转80°后的终边为终边所成的角就是-30°角.
练习
2.若90 <α<β<135 ,则α-β的范围是_______________,
α+β的范围是________________.
(-45 , 0 )
(180 , 270 )
知识探究(二)
思考1:为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,角的终边可能在哪些位置?
把角放在直角坐标系中,使:
(1)角的顶点与坐标原点重合;
(2)角的始边与x轴的非负半轴重合. 则
角的终边在第几象限,我们就说这个角是第几象限角.
角的终边在坐标轴限,我们就说这个角不属于任何象限,习惯上称为轴线角。
终边可能落在某个象限内,也可能落在坐标轴上。
象限角和轴线角
第一象限角
第二象限角
第三象限角
第四象限角
返回
练习
1.已知角的顶点与原点重合, 角的始边与x轴的非负半轴重合, 请作出下列各角,并指出它们各是哪个象限的角?
(1)420 , (2)-75 , (3)855 , (4) -510 .(教材P171第3题)
第一象限角
420
-75
第四象限角
855
第二象限角
-510
第三象限角
2.经过3小时15分,时钟的分针和时针旋转所形成的角各是多少,它们各是几象限角?
解:
解:
分针旋转所形成的角是-1170 ,
它是第四象限角;
时针针旋转所形成的角是
它是第三象限角.
-97.5 ,
思考2:将角按照上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线,以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
328°
-392°
设射线OB是-32°的终边,则
-392°,... , 328°,...的终边也是OB,
这些角与-32°相差360°的整数倍。即
这些角可以表示为
-32°+k·360°(k∈Z)
如328°=-32°+360°(这里k=_____)
328°=-32°-360° (这里k=_____)
1
-1
思考4:由以上你能得出什么结论?
与角α的终边相同的角有无数多个,它们之差相差360 的整数倍。这些角(含α本身)可以表示为都可以用α+k·360(k∈Z)来表示。
思考3:-32°本身能用这种形式表示吗?
-328-°=-32°-0×360° (这里k=0)
{β|β=α+k·360°,k∈Z},
一般地,所有与角α终边相同的角,连同角α在内所构成的集合可表示为:
终边相同角的表示
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
注意:
(1)k∈Z。
“ K > 0”表示β是将α的终边逆时针旋转得到的;
“K < 0”表示β是将α的终边顺时针旋转得到的;
“K = 0”表示β就是α本身。
(2)α是任意角;
(3)终边相同的角不一定相相等,它们有无数多个,它们之间差相差360 的整数倍
返回
例析
思考:通过本题,你能说说如何在给定的范围内求出与已知角α终边相同的角吗?
第1步:
写出与已知角α终边相同的角:α+k·360°,k∈Z,
第2步:
让k取适当的整数,让角α+k·360°落在给定的范围内。
练习
(教材P171练习第4题)
(教材P171练习第4题)
例析
返回
思考:利用本题的方法(先在0°~360°内找出该角,再时上360°的整数倍),你能说说各象限角所组成的集合各是怎样的吗?
返回
练习
2.今天是星期三, 则7k(k∈Z)天后的那一天是星期几 7k(k∈Z)
天前的那一天是星期几 100天后的那一天是星期几
7k(k∈Z)天后和7k天前的那一天都是星期三
∵100=14×7+2
∴100天后的那一天是星期五
1.什么是锐角 它是几象限角,反过来成立吗
钝角呢?直角呢?
角的概念
1. 请说说角的概念是怎样扩展的?
小结
3.如何将角放在平面直角坐标系中?什么是象限角,轴线角?
(0°~360°)
不限制旋转量
对不同旋转方向作出区分
(任意角)
2.任意角怎样进行加减运算?其几何意义是怎样的?
0°~360°的角不够用
放在坐标系中
看终边的位置
如何表示象限角,轴线角?
4.与α终边相现的角如何表示?如何在给定的范围找出与已知角终边相同的角?
α+k·360°,k∈Z
先写出与已知角α终边相同的角:α+k·360°,k∈Z,
再让k取适当的整数,让角α+k·360°落在给定的范围内。
作业
1.教材P175习题5.1第1, 2(3)(4)(7)(8)题
2.写出终边在阴影部分中的角的集合:
(1)
(2)
3.(选做题)试完成下表:
α,2α, 的终边所在的位置
α 一象限 二象限 三象限 四象限
2α
一、三象限前半区
一、三象限后半区
二、四象限前半区
二、四象限后半区
x轴上半区
x轴上半区
x轴下半区
x轴下半区
2.
(1)
(2)
再 见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
