数学人教A版(2019)必修第一册5.1.2弧度制(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2弧度制(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
5.1任意角和弧度制
5.1.2 弧度制
引入
在古典小说中,我们经常会看某人动不动就身长“七尺”,“八尺”,甚至“一丈”,而在现代,2米以上的人并不多见,何也,难道古人真的普遍比现代人高很多?对于钻石的大小,我们有时说多少多少克拉,有时又说是多少多少克;称时体重,中国人常说多少多少斤,西方人常说多少多少磅,...., 这些听起来总有些让人糊涂,原因又是什么呢?
对于同一种量,衡量时采用是不同的单位制。
度量长度,可以用米,英尺,码,市尺等不同的单位制,度量质量也可以用千克,磅等不同的单位制. 在不同的地域,不同的场景,不同的习惯中,这样的不同单位制,往往能给解决问题带来方便。
那么角的大小是否也可以用不同的单位制呢?又能否象度量长度那样,用十进制的实数来度量角的大小呢?接下来我们就来研究这个问题。
1′=60″
因此,周角=360°,平角=180°,直角=90°。
思考1:回忆一下,在以前,角的大小我们一般用什么单位制来度量?它的规定是怎样的?
度(°),分('),秒(″)的关系是:
角度制。
其基本单位是“度(°)”,其下还有“分(')”和“秒(″)”
1°=60′
思考2:角度制下,扇形的弧长和面积公式是怎样的?
思考3:你能说说角度制在一些场合(比如函数)的局限吗?
我们知知道,函数是非空实数集到实数集的对应关系,而实数采用的是十进制 。为了研究周期性的变化现象,我们现在需要建立任意角的三角函数,而角度制下的角却是六十进制,也就是说,自变量的集合不满足十进制,这是与函数的定义不吻合的.
另外,很多时候,周期性现象中的变量也不都是角,有可能还有时间,位移等十进制的量,而在解决实际问题的过程中,有时需要同时应用几种不同类型的函数,也就可能出现角与实数进行运算的情况,这时,如果角仍是角度制下六十进制,那就没法进行了,而且其中的意义也不得而知。
所以,为了满足函数的定义,为了解决三角函数的适用性,迫切需要引入一种新的单位制来度量角,在这种单位制下,角最好能象实数一样进行十进制的运算,甚至可以直接和实数进行运算。
这种单位制就是弧度制. 它采用弧度作为角的单位
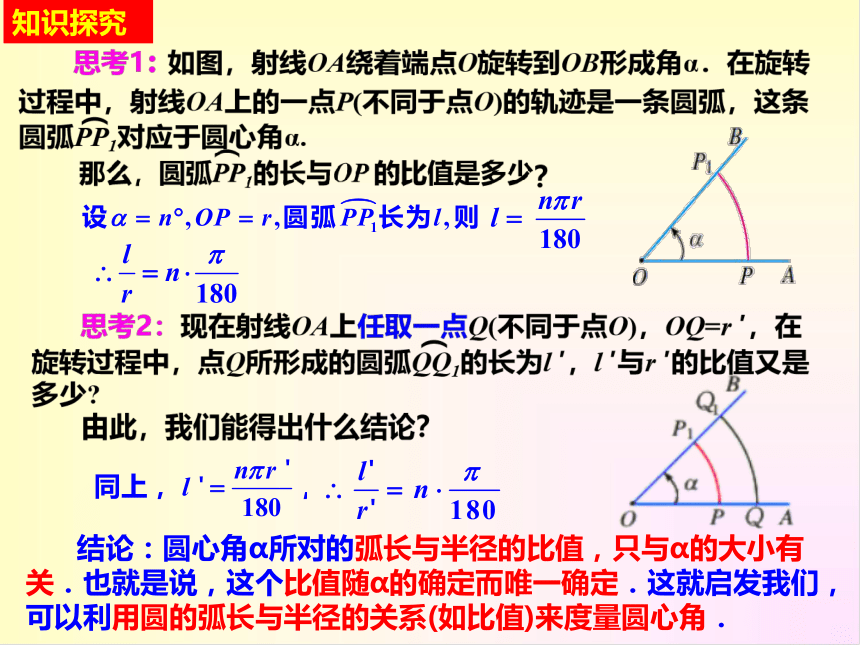
知识探究
结论:圆心角α所对的弧长与半径的比值,只与α的大小有关.也就是说,这个比值随α的确定而唯一确定.这就启发我们,可以利用圆的弧长与半径的关系(如比值)来度量圆心角.
弧度的单位
可以省略不写
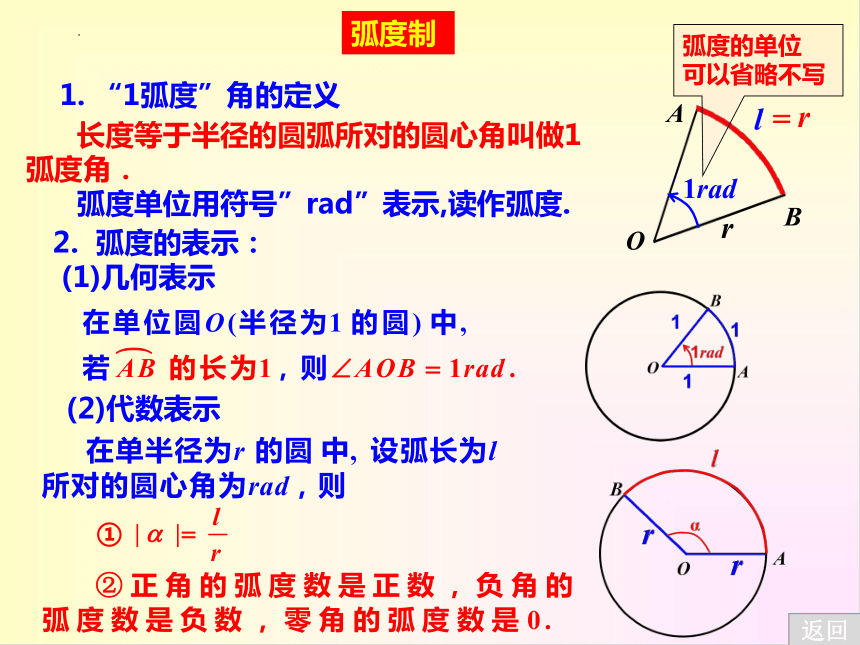
1. “1弧度”角的定义
长度等于半径的圆弧所对的圆心角叫做1弧度角.
弧度单位用符号”rad”表示,读作弧度.
弧度制
1rad
2. 弧度的表示:
(1)几何表示
(2)代数表示
返回
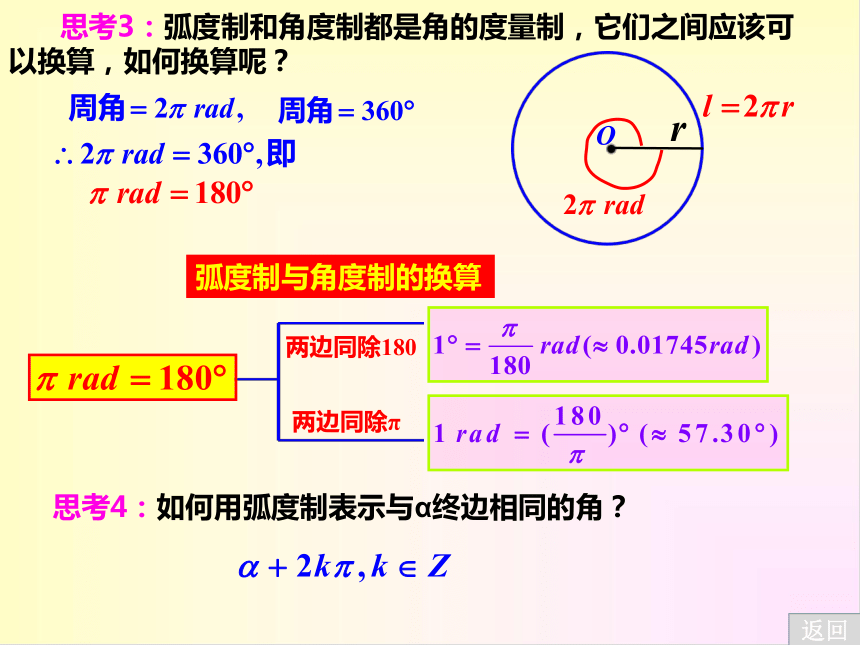
思考3:弧度制和角度制都是角的度量制,它们之间应该可以换算,如何换算呢?
弧度制与角度制的换算
两边同除180
两边同除π
返回
思考4:如何用弧度制表示与α终边相同的角?
例1.(1) 按下列要求,把67°30′化成弧度:
①精确值; ②近似值(精确到0.001)。
解:①
例析
例1.(2) 按下列要求,把3.14rad化成角度:
(1)精确值; (2)近似值(精确到0.001)。
解:(1)
说明:
(1)若无特别要求,互化结果一般取精确值,不将π化成小数;
(2)弧度单位可省略不写,如
角度制与弧度制的比较
(1)角度制与弧度制都是度量角的单位制
(2)弧度制的单位是“弧度(rad)”,1弧度角等于半径长的圆弧所对的圆心角. 用弧度表示角的大小时, 单位通常省略不写.
角度制的单位是“度(°)”,其下还有分(′),秒(″),1度角等于周角的1/360. 用角度表示角的大小时,单位不能省略。
(3)角度制是以“角量角”,弧度制都是以“以弧量角”, 但不论以哪种单位制来度量角,圆心角的大小都与半径大小无关.
(4)弧度制的是“十进制”,角度制是“六十进制”;
(5)角度与弧度的基本换算关系:
思考5:你能将角度制和弧度制作一个比较吗?
注意:
表示角时,两种单位不能“混用”.如下列写法都是错误的:
返回
部分特殊角的角度与弧度
180°=π rad
一一对应的关系。即
每个角都有唯一的实数(等于这个叫的弧度);
每个实数也都有唯一一个对应的角(弧度数等于这个实数).
思考6:请完成下表
思考6: 你能说说角的概念推广以后,在弧度制下,角的集合与实数集R之间的对应关系是怎样的?
角的集合
正角
零角
负角
实数集R
正数
零
负数
对应角的弧度数
返回
轴线角和象限角的表示
(1)轴线角的表示:
x 轴非负半轴上的角:
x 轴非正半轴上的角:
y 轴非负半轴上的角:
y 轴非正半轴上的角:
x 轴上的角:
y 轴上的角:
(2)象限角的表示:
第一象限角:
第二象限角:
第三象限角:
第四象限角:
返回
练习
(教材P175练习第1,2题)
解:(1)
例析
α
弧度制下扇形的弧长和面积公式
(1)弧长公式:
(2)扇形面积公式:
返回
例3. 一扇形周长为10cm,当扇形的圆心角等于多少时,这个扇形的面积最大?并求此扇形的最大面积.
解:
例析
练 习
1.分别用角度制,弧度制下的弧长公式计算半径为1cm的圆中,60°的圆心角对对弧的长度。
2.已知半径为120mm的圆上,有一条弧长为144mm,求该弧所对圆心的弧度数和角度数。
3.已知扇形的周长为8cm,圆心角为2。求该扇形的面积.
课堂小结
1.为什么要引入弧度制,用弧度制度量角合理吗?
2. 什么是1弧度角,它的几何表示和代数表示各是怎样的?
3. 弧度制与角度制怎样进行换算?它们之间有可异同?
4. 特殊角,象限角,轴线角用弧度怎样表示?
5.弧度制下,扇形的弧长和面积怎样计算?
作 业
教材P176习题5.1.
1. 第4, 5, 8, 9题(各题的结果取准确值)
2.(选做题)第10题(结果取准确值)
再见
5.1任意角和弧度制
5.1.2 弧度制
引入
在古典小说中,我们经常会看某人动不动就身长“七尺”,“八尺”,甚至“一丈”,而在现代,2米以上的人并不多见,何也,难道古人真的普遍比现代人高很多?对于钻石的大小,我们有时说多少多少克拉,有时又说是多少多少克;称时体重,中国人常说多少多少斤,西方人常说多少多少磅,...., 这些听起来总有些让人糊涂,原因又是什么呢?
对于同一种量,衡量时采用是不同的单位制。
度量长度,可以用米,英尺,码,市尺等不同的单位制,度量质量也可以用千克,磅等不同的单位制. 在不同的地域,不同的场景,不同的习惯中,这样的不同单位制,往往能给解决问题带来方便。
那么角的大小是否也可以用不同的单位制呢?又能否象度量长度那样,用十进制的实数来度量角的大小呢?接下来我们就来研究这个问题。
1′=60″
因此,周角=360°,平角=180°,直角=90°。
思考1:回忆一下,在以前,角的大小我们一般用什么单位制来度量?它的规定是怎样的?
度(°),分('),秒(″)的关系是:
角度制。
其基本单位是“度(°)”,其下还有“分(')”和“秒(″)”
1°=60′
思考2:角度制下,扇形的弧长和面积公式是怎样的?
思考3:你能说说角度制在一些场合(比如函数)的局限吗?
我们知知道,函数是非空实数集到实数集的对应关系,而实数采用的是十进制 。为了研究周期性的变化现象,我们现在需要建立任意角的三角函数,而角度制下的角却是六十进制,也就是说,自变量的集合不满足十进制,这是与函数的定义不吻合的.
另外,很多时候,周期性现象中的变量也不都是角,有可能还有时间,位移等十进制的量,而在解决实际问题的过程中,有时需要同时应用几种不同类型的函数,也就可能出现角与实数进行运算的情况,这时,如果角仍是角度制下六十进制,那就没法进行了,而且其中的意义也不得而知。
所以,为了满足函数的定义,为了解决三角函数的适用性,迫切需要引入一种新的单位制来度量角,在这种单位制下,角最好能象实数一样进行十进制的运算,甚至可以直接和实数进行运算。
这种单位制就是弧度制. 它采用弧度作为角的单位
知识探究
结论:圆心角α所对的弧长与半径的比值,只与α的大小有关.也就是说,这个比值随α的确定而唯一确定.这就启发我们,可以利用圆的弧长与半径的关系(如比值)来度量圆心角.
弧度的单位
可以省略不写
1. “1弧度”角的定义
长度等于半径的圆弧所对的圆心角叫做1弧度角.
弧度单位用符号”rad”表示,读作弧度.
弧度制
1rad
2. 弧度的表示:
(1)几何表示
(2)代数表示
返回
思考3:弧度制和角度制都是角的度量制,它们之间应该可以换算,如何换算呢?
弧度制与角度制的换算
两边同除180
两边同除π
返回
思考4:如何用弧度制表示与α终边相同的角?
例1.(1) 按下列要求,把67°30′化成弧度:
①精确值; ②近似值(精确到0.001)。
解:①
例析
例1.(2) 按下列要求,把3.14rad化成角度:
(1)精确值; (2)近似值(精确到0.001)。
解:(1)
说明:
(1)若无特别要求,互化结果一般取精确值,不将π化成小数;
(2)弧度单位可省略不写,如
角度制与弧度制的比较
(1)角度制与弧度制都是度量角的单位制
(2)弧度制的单位是“弧度(rad)”,1弧度角等于半径长的圆弧所对的圆心角. 用弧度表示角的大小时, 单位通常省略不写.
角度制的单位是“度(°)”,其下还有分(′),秒(″),1度角等于周角的1/360. 用角度表示角的大小时,单位不能省略。
(3)角度制是以“角量角”,弧度制都是以“以弧量角”, 但不论以哪种单位制来度量角,圆心角的大小都与半径大小无关.
(4)弧度制的是“十进制”,角度制是“六十进制”;
(5)角度与弧度的基本换算关系:
思考5:你能将角度制和弧度制作一个比较吗?
注意:
表示角时,两种单位不能“混用”.如下列写法都是错误的:
返回
部分特殊角的角度与弧度
180°=π rad
一一对应的关系。即
每个角都有唯一的实数(等于这个叫的弧度);
每个实数也都有唯一一个对应的角(弧度数等于这个实数).
思考6:请完成下表
思考6: 你能说说角的概念推广以后,在弧度制下,角的集合与实数集R之间的对应关系是怎样的?
角的集合
正角
零角
负角
实数集R
正数
零
负数
对应角的弧度数
返回
轴线角和象限角的表示
(1)轴线角的表示:
x 轴非负半轴上的角:
x 轴非正半轴上的角:
y 轴非负半轴上的角:
y 轴非正半轴上的角:
x 轴上的角:
y 轴上的角:
(2)象限角的表示:
第一象限角:
第二象限角:
第三象限角:
第四象限角:
返回
练习
(教材P175练习第1,2题)
解:(1)
例析
α
弧度制下扇形的弧长和面积公式
(1)弧长公式:
(2)扇形面积公式:
返回
例3. 一扇形周长为10cm,当扇形的圆心角等于多少时,这个扇形的面积最大?并求此扇形的最大面积.
解:
例析
练 习
1.分别用角度制,弧度制下的弧长公式计算半径为1cm的圆中,60°的圆心角对对弧的长度。
2.已知半径为120mm的圆上,有一条弧长为144mm,求该弧所对圆心的弧度数和角度数。
3.已知扇形的周长为8cm,圆心角为2。求该扇形的面积.
课堂小结
1.为什么要引入弧度制,用弧度制度量角合理吗?
2. 什么是1弧度角,它的几何表示和代数表示各是怎样的?
3. 弧度制与角度制怎样进行换算?它们之间有可异同?
4. 特殊角,象限角,轴线角用弧度怎样表示?
5.弧度制下,扇形的弧长和面积怎样计算?
作 业
教材P176习题5.1.
1. 第4, 5, 8, 9题(各题的结果取准确值)
2.(选做题)第10题(结果取准确值)
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
