人教版八年级上册11.2.2 三角形的外角 课件(共29张PPT)
文档属性
| 名称 | 人教版八年级上册11.2.2 三角形的外角 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 11:10:22 | ||
图片预览






文档简介
(共29张PPT)
11.2.2
字符延长
三
角
形
的
外
角
The Outer Angle of a triangle
理解三角形的外角的定义并能识别三角形的外角
理解三角形外角的性质,能够用三角形外角性质求与三角形有关角的度数
掌握三角形外角的性质,能利用三角形外角的性质解决生活中的实际问题.
01
02
03
教学目标
重点
难点
1.三角形的外角的性质
教学重难点
2.三角形外角和定理
三角形外角的定义及三角形外角和定理
的论证过程
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
复习导入
1.什么是三角形的内角?三角形的内角和等于多少度
2.在△ABC中,∠A = 60°, ∠B = 65°,则∠C = .
三角形相邻两边组成的角叫做三角形的内角,三角形的内 角和为180°
55 °
3.在△ABC 中,∠A = 30°, ∠B =∠C,则∠C = .
75°
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
探究新知:三角形外角的概念
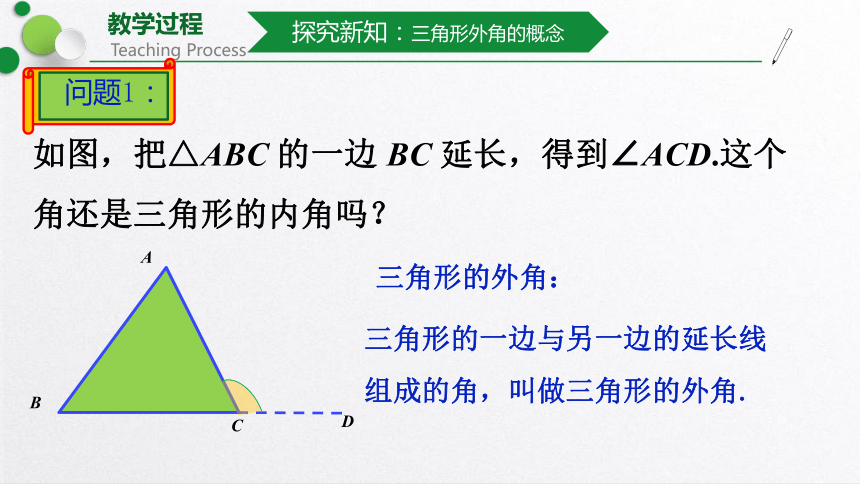
如图,把△ABC 的一边 BC 延长,得到∠ACD.这个角还是三角形的内角吗?
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
问题1:
A
C
B
D
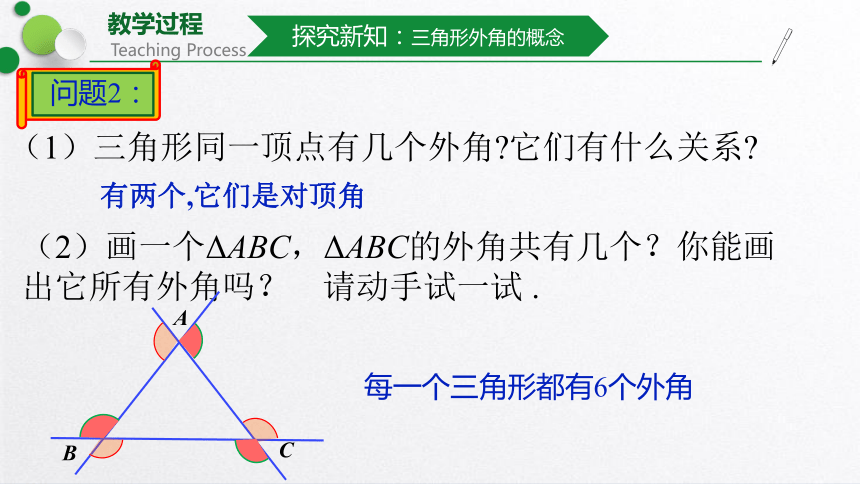
(2)画一个ΔABC,ΔABC的外角共有几个?你能画出它所有外角吗? 请动手试一试 .
(1)三角形同一顶点有几个外角 它们有什么关系
有两个,它们是对顶角
每一个三角形都有6个外角
问题2:
探究新知:三角形外角的概念
A
B
C
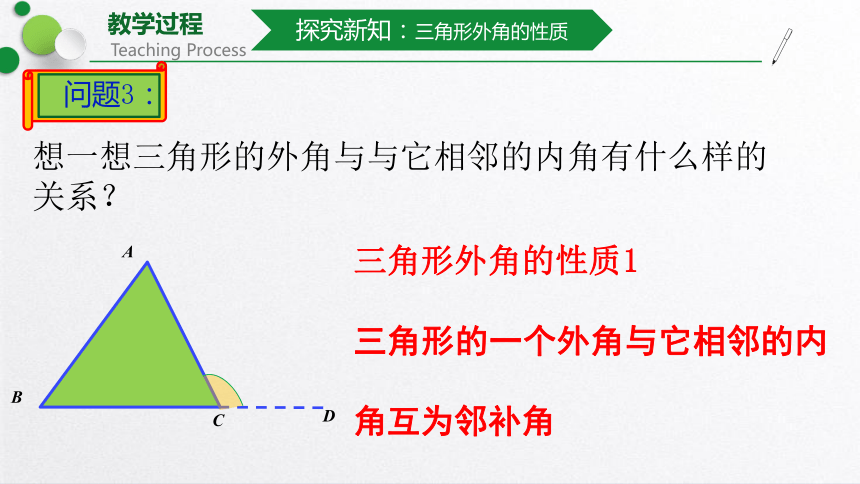
想一想三角形的外角与与它相邻的内角有什么样的关系?
三角形外角的性质1
三角形的一个外角与它相邻的内角互为邻补角
问题3:
探究新知:三角形外角的性质
A
C
B
D
A
B
C
D
如图,在△ABC 中,∠A=80°, ∠B=50°,则∠ACD = 。∠ACD与∠A,∠B有什么关系?并说明理由
任意一个三角形的一个外角与它不相邻的两个内角是否都有以上中这种关系呢?(同学们自己动手证明)
130 °
∠ACD= ∠A+ ∠B
探究新知:三角形外角的性质
问题4:
A
B
C
D
1.如图在△ABC中 ,
求:∠ACD= ∠A+ ∠B
解:
三角形外角的性质2:
三角形的一个外角等于与它不相邻的两个内角的和
∵ ∠ACD +∠ACB = 180°
∠A +∠B +∠ACB = 180°
∴ ∠ACD =∠A +∠B
探究新知:三角形外角的性质
A
B
C
D
1. 如图在△ABC 中,
求∠ACD= ∠A+ ∠B
解:过C作CE平行于AB
∵CE∥ AB
∴∠A =∠1(两直线平行,内错角相等)
∠B =∠2 (两直线平行,同位角相等)
又∵ ∠ACD =∠1 +∠2
∴∠ACD =∠A +∠B
探究新知:三角形外角的性质
B
A
C
D
E
1
2
你们知道三角形的外角与与它不相邻的两个内角有怎样的大小关系吗?
三角形外角的性质3:
三角形的一个外角大于与它不相邻的任何一个内角.
∠ACD> ∠A, ∠ACD> ∠B
A
B
C
D
探究新知:三角形外角的性质
∠ACD= ∠A+ ∠B
问题5:
学以致用
∠1=95°
∠1=51°
∠1=80°
1.求下列各图中∠1的度数
35°
1
50°
86°
35°
1
30°
50°
1
学以致用
3.当∠A=85°,∠B = 30°,∠C = 20°,求∠1, ∠2的度数
∠2= ∠A+ ∠C= 105°
∠1= ∠2+ ∠B=135°
2.把图中∠A、 ∠2、 ∠3按由大到小的顺序排列
∠1> ∠2 > ∠A
A
B
C
D
1
2
结论归纳
三角形的内角与外角的关系:
1. 三角形的一个外角与它相邻的内角互补
2.三角形的一个外角等于与它不相邻的两个内角的和 .
三角形内角和定理的推论
三角形的一个外角等于与它不相邻的两个内角的和
3.三角形的一个外角大于任意一个与它不相邻的内角 .
三角形的外角和
三角形每个顶点处分别有两个外角,并且这两个角相等,如果我们每个顶点处各取一个外角,那么这三个角的和就叫三角形的外角和.
思考
∠1+ ∠2 +∠3=?
方法:度量法,拼角法,几何推理证明
探究新知:三角形外角的外角和
2
3
1
A
B
C
三角形的外角和
思考
∠1+ ∠2 +∠3=?
证法一:
∵ ∠1= ∠ABC + ∠ ACB
∠2 =∠BAC+ ∠ACB
∠3 =∠BAC+ ∠ABC
∴∠1+∠2 +∠3 =2(∠ABC +∠BAC +∠ACB)
∵ ∠ABC +∠BAC +∠ACB =180°,
∴ ∠1 +∠2 +∠3= 2×180°=360°
探究新知:三角形外角的外角和
2
3
1
A
B
C
三角形的外角和
思考
∠1+ ∠2 +∠3=?
证法二:
∵ ∠1+∠BAC= 180°
∠2+∠ABC= 180°
∠3+∠ACB= 180°
三角形的外角和为360°
∴ ∠1+∠BAC+ ∠2+∠ABC+ ∠3+∠ACB= 540°
∵ ∠ABC +∠BAC +∠ACB =180°,
∴ ∠1 +∠2 +∠3= 540° - 180° =360°
探究新知:三角形外角的外角和
2
3
1
A
B
C
三角形的外角和
思考
∠1+ ∠2 +∠3=?
证法三:
三角形的外角和为360°
探究新知:三角形外角的外角和
D
3
1
2
A
B
C
过点B作AC的平行线BD
∵BD∥AC
∴∠EBD=∠1(两直线平行,同位角相等)
∠CBD=∠3(两直线平行,同位角相等)
E
∵∠2+∠EBD+∠CBD=360°,
∴∠1+∠2+∠3=360°.
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
1.三角形外角性质辨析,判读下列说法是否正确
① 三角形的外角和是指三角形所有外角的和
② 三角形的外角和等于它内角和的 2 倍
③ 三角形的一个外角等于两个内角的和
④ 三角形的一个外角等于与它不相邻的两个内角的和
⑤ 三角形的一个外角大于任何一个内角
巩固新知
X
√
X
√
X
巩固新知
2.已知△ABC的一个外角为70°,则△ABC一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3. 如图∠1,∠2,∠3是△ABC 的三个外角,∠2=135°,
则∠1+∠3=
225°
2
3
1
A
B
C
C
巩固新知
4. 直尺与含30°的三角板组合图形中,求∠1的度数
25°
1
答案:55°
巩固新知
解:
∵ ∠ACD=∠A+∠B
∠A=70°,∠B=40°
∴∠ACD = 40°+ 70°=110°
∵ CE平分∠ACD
∴∠1= ∠ACD=55°
5.如图,∠A=70°,∠B=40°,CE平分∠ACD,求∠1的度数
A
B
C
D
E
40°
1
70°
巩固新知
6.如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=65°,∠ACD=30°,∠ABE=20°,则∠BFC =_______ .
解:∵ ∠BDF =∠A +∠ACD
∠A= 65°,∠ACD = 30°
∴ ∠BDF = 65°+30°=95°
∵ ∠BFC = ∠BDF +∠ABE
∠ABE =20°
∴ ∠BFC = 95°+ 20° = 115°
A
D
B
E
C
F
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
01
定义
03
外角和
02
外角性质
三角形的外角的和等于360 °
三角形的一边与另一边的延长线组成的角,叫做三角形的外角
课堂小结
1.三角形的一个外角与它相邻内角互为邻补角
2.三角形的一个外角等于与它不相邻的两个内角的和
3.三角形的一个外角大于任何一个与它不相邻的内角
聆
听
谢
谢
11.2.2
字符延长
三
角
形
的
外
角
The Outer Angle of a triangle
理解三角形的外角的定义并能识别三角形的外角
理解三角形外角的性质,能够用三角形外角性质求与三角形有关角的度数
掌握三角形外角的性质,能利用三角形外角的性质解决生活中的实际问题.
01
02
03
教学目标
重点
难点
1.三角形的外角的性质
教学重难点
2.三角形外角和定理
三角形外角的定义及三角形外角和定理
的论证过程
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
复习导入
1.什么是三角形的内角?三角形的内角和等于多少度
2.在△ABC中,∠A = 60°, ∠B = 65°,则∠C = .
三角形相邻两边组成的角叫做三角形的内角,三角形的内 角和为180°
55 °
3.在△ABC 中,∠A = 30°, ∠B =∠C,则∠C = .
75°
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
探究新知:三角形外角的概念
如图,把△ABC 的一边 BC 延长,得到∠ACD.这个角还是三角形的内角吗?
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
问题1:
A
C
B
D
(2)画一个ΔABC,ΔABC的外角共有几个?你能画出它所有外角吗? 请动手试一试 .
(1)三角形同一顶点有几个外角 它们有什么关系
有两个,它们是对顶角
每一个三角形都有6个外角
问题2:
探究新知:三角形外角的概念
A
B
C
想一想三角形的外角与与它相邻的内角有什么样的关系?
三角形外角的性质1
三角形的一个外角与它相邻的内角互为邻补角
问题3:
探究新知:三角形外角的性质
A
C
B
D
A
B
C
D
如图,在△ABC 中,∠A=80°, ∠B=50°,则∠ACD = 。∠ACD与∠A,∠B有什么关系?并说明理由
任意一个三角形的一个外角与它不相邻的两个内角是否都有以上中这种关系呢?(同学们自己动手证明)
130 °
∠ACD= ∠A+ ∠B
探究新知:三角形外角的性质
问题4:
A
B
C
D
1.如图在△ABC中 ,
求:∠ACD= ∠A+ ∠B
解:
三角形外角的性质2:
三角形的一个外角等于与它不相邻的两个内角的和
∵ ∠ACD +∠ACB = 180°
∠A +∠B +∠ACB = 180°
∴ ∠ACD =∠A +∠B
探究新知:三角形外角的性质
A
B
C
D
1. 如图在△ABC 中,
求∠ACD= ∠A+ ∠B
解:过C作CE平行于AB
∵CE∥ AB
∴∠A =∠1(两直线平行,内错角相等)
∠B =∠2 (两直线平行,同位角相等)
又∵ ∠ACD =∠1 +∠2
∴∠ACD =∠A +∠B
探究新知:三角形外角的性质
B
A
C
D
E
1
2
你们知道三角形的外角与与它不相邻的两个内角有怎样的大小关系吗?
三角形外角的性质3:
三角形的一个外角大于与它不相邻的任何一个内角.
∠ACD> ∠A, ∠ACD> ∠B
A
B
C
D
探究新知:三角形外角的性质
∠ACD= ∠A+ ∠B
问题5:
学以致用
∠1=95°
∠1=51°
∠1=80°
1.求下列各图中∠1的度数
35°
1
50°
86°
35°
1
30°
50°
1
学以致用
3.当∠A=85°,∠B = 30°,∠C = 20°,求∠1, ∠2的度数
∠2= ∠A+ ∠C= 105°
∠1= ∠2+ ∠B=135°
2.把图中∠A、 ∠2、 ∠3按由大到小的顺序排列
∠1> ∠2 > ∠A
A
B
C
D
1
2
结论归纳
三角形的内角与外角的关系:
1. 三角形的一个外角与它相邻的内角互补
2.三角形的一个外角等于与它不相邻的两个内角的和 .
三角形内角和定理的推论
三角形的一个外角等于与它不相邻的两个内角的和
3.三角形的一个外角大于任意一个与它不相邻的内角 .
三角形的外角和
三角形每个顶点处分别有两个外角,并且这两个角相等,如果我们每个顶点处各取一个外角,那么这三个角的和就叫三角形的外角和.
思考
∠1+ ∠2 +∠3=?
方法:度量法,拼角法,几何推理证明
探究新知:三角形外角的外角和
2
3
1
A
B
C
三角形的外角和
思考
∠1+ ∠2 +∠3=?
证法一:
∵ ∠1= ∠ABC + ∠ ACB
∠2 =∠BAC+ ∠ACB
∠3 =∠BAC+ ∠ABC
∴∠1+∠2 +∠3 =2(∠ABC +∠BAC +∠ACB)
∵ ∠ABC +∠BAC +∠ACB =180°,
∴ ∠1 +∠2 +∠3= 2×180°=360°
探究新知:三角形外角的外角和
2
3
1
A
B
C
三角形的外角和
思考
∠1+ ∠2 +∠3=?
证法二:
∵ ∠1+∠BAC= 180°
∠2+∠ABC= 180°
∠3+∠ACB= 180°
三角形的外角和为360°
∴ ∠1+∠BAC+ ∠2+∠ABC+ ∠3+∠ACB= 540°
∵ ∠ABC +∠BAC +∠ACB =180°,
∴ ∠1 +∠2 +∠3= 540° - 180° =360°
探究新知:三角形外角的外角和
2
3
1
A
B
C
三角形的外角和
思考
∠1+ ∠2 +∠3=?
证法三:
三角形的外角和为360°
探究新知:三角形外角的外角和
D
3
1
2
A
B
C
过点B作AC的平行线BD
∵BD∥AC
∴∠EBD=∠1(两直线平行,同位角相等)
∠CBD=∠3(两直线平行,同位角相等)
E
∵∠2+∠EBD+∠CBD=360°,
∴∠1+∠2+∠3=360°.
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
1.三角形外角性质辨析,判读下列说法是否正确
① 三角形的外角和是指三角形所有外角的和
② 三角形的外角和等于它内角和的 2 倍
③ 三角形的一个外角等于两个内角的和
④ 三角形的一个外角等于与它不相邻的两个内角的和
⑤ 三角形的一个外角大于任何一个内角
巩固新知
X
√
X
√
X
巩固新知
2.已知△ABC的一个外角为70°,则△ABC一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
3. 如图∠1,∠2,∠3是△ABC 的三个外角,∠2=135°,
则∠1+∠3=
225°
2
3
1
A
B
C
C
巩固新知
4. 直尺与含30°的三角板组合图形中,求∠1的度数
25°
1
答案:55°
巩固新知
解:
∵ ∠ACD=∠A+∠B
∠A=70°,∠B=40°
∴∠ACD = 40°+ 70°=110°
∵ CE平分∠ACD
∴∠1= ∠ACD=55°
5.如图,∠A=70°,∠B=40°,CE平分∠ACD,求∠1的度数
A
B
C
D
E
40°
1
70°
巩固新知
6.如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=65°,∠ACD=30°,∠ABE=20°,则∠BFC =_______ .
解:∵ ∠BDF =∠A +∠ACD
∠A= 65°,∠ACD = 30°
∴ ∠BDF = 65°+30°=95°
∵ ∠BFC = ∠BDF +∠ABE
∠ABE =20°
∴ ∠BFC = 95°+ 20° = 115°
A
D
B
E
C
F
目 录
CONTENTS
复习导入
教学过程
巩固新知
课堂小结
01
定义
03
外角和
02
外角性质
三角形的外角的和等于360 °
三角形的一边与另一边的延长线组成的角,叫做三角形的外角
课堂小结
1.三角形的一个外角与它相邻内角互为邻补角
2.三角形的一个外角等于与它不相邻的两个内角的和
3.三角形的一个外角大于任何一个与它不相邻的内角
聆
听
谢
谢
