第十六章 轴对称和中心对称 全章综合测评卷(含解析) 2023—2024学年冀教版数学八年级上册
文档属性
| 名称 | 第十六章 轴对称和中心对称 全章综合测评卷(含解析) 2023—2024学年冀教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 721.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 13:03:09 | ||
图片预览



文档简介
第十六章 轴对称和中心对称
作答时间:120分钟 总分:120分
一、选择题(本大题有16个小题,每小题3分,共48分)
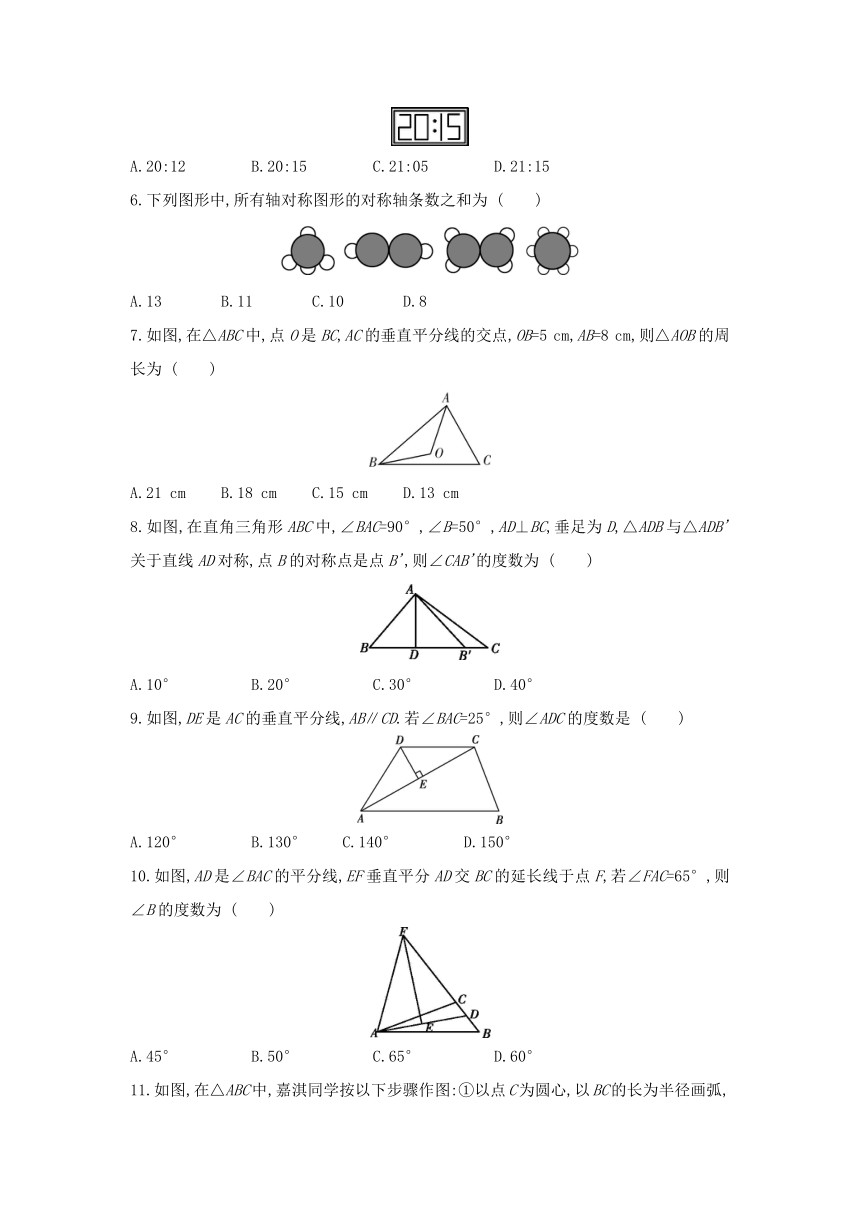
1.下列图形中,是轴对称图形,但不是中心对称图形的是 ( )
2.已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,则点M一定在 ( )
A.AC边的高上
B.AB边的中线上
C.BC边的垂直平分线上
D.∠A的平分线上
3.利用图形的旋转可以设计出许多美丽的图案.如图2中的图案是由图1所示的基本图案以点O为旋转中心,顺时针(或逆时针)连续旋转,每次旋转α角构成,则α为 ( )
A.36° B.72° C.144° D.216°
4.剪纸是我国传统的民间艺术.将一张纸片按图①,②中的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是 ( )
5.从平面镜里看到背后墙上电子钟的示数如图所示,这时的正确时间是 ( )
A.20:12 B.20:15 C.21:05 D.21:15
6.下列图形中,所有轴对称图形的对称轴条数之和为 ( )
A.13 B.11 C.10 D.8
7.如图,在△ABC中,点O是BC,AC的垂直平分线的交点,OB=5 cm,AB=8 cm,则△AOB的周长为 ( )
A.21 cm B.18 cm C.15 cm D.13 cm
8.如图,在直角三角形ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 ( )
A.10° B.20° C.30° D.40°
9.如图,DE是AC的垂直平分线,AB∥CD.若∠BAC=25°,则∠ADC的度数是 ( )
A.120° B.130° C.140° D.150°
10.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为 ( )
A.45° B.50° C.65° D.60°
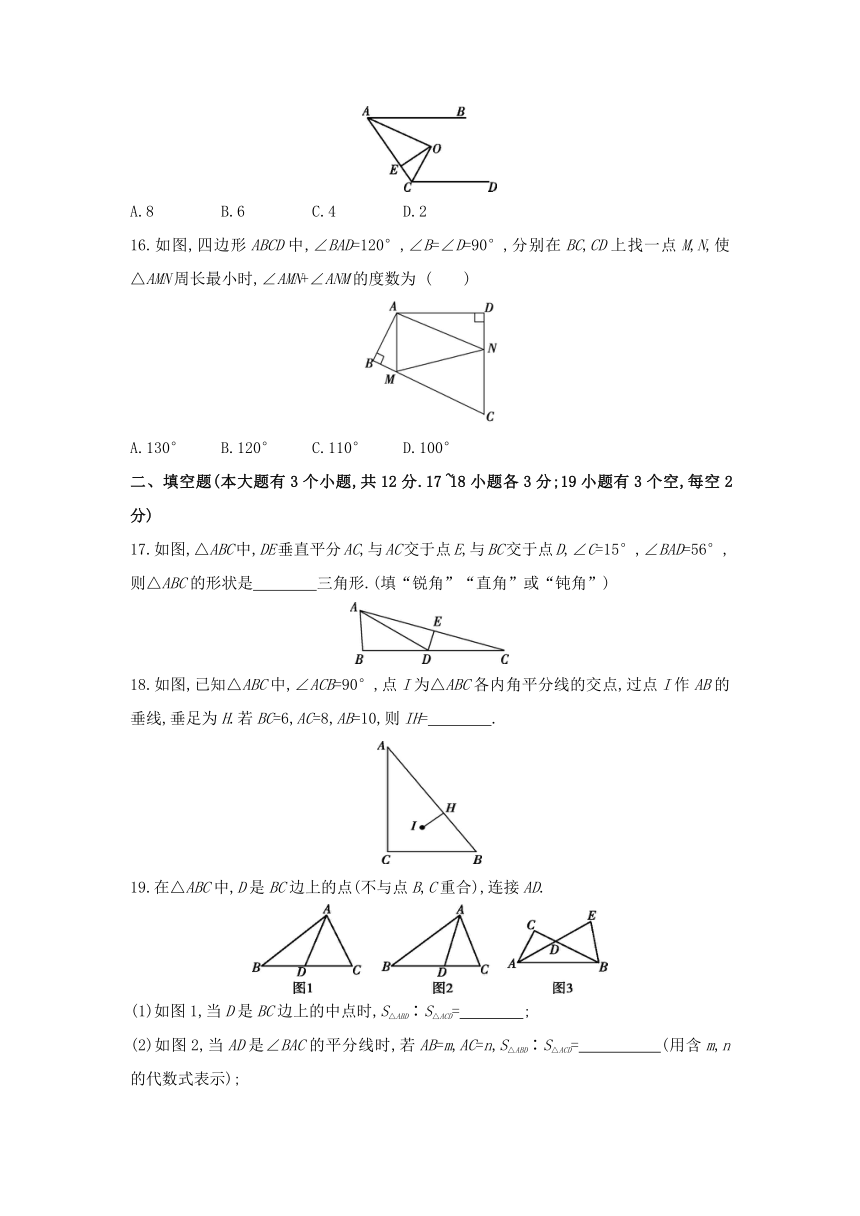
11.如图,在△ABC中,嘉淇同学按以下步骤作图:①以点C为圆心,以BC的长为半径画弧,交AC于点D,连接BD;②分别以点B,D为圆心,以大于BD的长为半径画弧,两弧交于点E;③作射线CE交BD于点F,连接AF.
若△ABC的面积为10,则△ACF的面积为 ( )
A.2.5 B.5 C.7.5 D.8
12.如图,△ABC的外角∠ACD的平分线CO与∠ABC的平分线BO相交于点O,连接OA.若∠BAC=50°,则∠CAO的度数为 ( )
A.50° B.55° C.60° D.65°
13.如图,在长方形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠,使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为 ( )
A.15 B.20 C.25 D.30
14.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是 ( )
A.24 B.30 C.36 D.42
15.如图,AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于点E.若OE=2,则AB与CD之间的距离是 ( )
A.8 B.6 C.4 D.2
16.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,分别在BC,CD上找一点M,N,使△AMN周长最小时,∠AMN+∠ANM的度数为 ( )
A.130° B.120° C.110° D.100°
二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)
17.如图,△ABC中,DE垂直平分AC,与AC交于点E,与BC交于点D,∠C=15°,∠BAD=56°,则△ABC的形状是 三角形.(填“锐角”“直角”或“钝角”)
18.如图,已知△ABC中,∠ACB=90°,点I为△ABC各内角平分线的交点,过点I作AB的垂线,垂足为H.若BC=6,AC=8,AB=10,则IH= .
19.在△ABC中,D是BC边上的点(不与点B,C重合),连接AD.
(1)如图1,当D是BC边上的中点时,S△ABD∶S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD∶S△ACD= (用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
三、解答题(本大题有6个小题,共60分)
20.(8分)如图,甲和乙是全等图形,但两个四边形的顶点字母不同.
(1)请从下列序号中选择正确选项的序号填写:①点E,F,G,H;②点G,F,E,H;③点E,H,G,F;④点G,H,E,F.
如果甲经过一次平移后得到乙,那么点A,B,C,D的对应点依次为 ;
如果甲经过一次轴对称后得到乙,那么点A,B,C,D的对应点依次为 ;
如果甲经过中心对称后得到乙,那么点A,B,C,D的对应点依次为 .
(2)如果甲与乙关于O点成中心对称,请画出对称中心.(保留作图痕迹,不写作法)
(3)如果甲与乙关于直线m成轴对称,请你利用尺规作图画出直线m.(保留作图痕迹,不写作法)
21.(9分)如图,在△ABC中,∠A=40°,∠C=60°.
(1)用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求∠BDC的度数.
22.(10分)如图,在△ABC中,AP平分∠BAC,PE⊥AB于点E,PF⊥AC交AC的延长线于点F,BE=CF.求证:点P在BC的垂直平分线上.
23.(10分)如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
24.(11分)已知∠AOB=90°,OC为∠AOB的平分线.
(1)如图1,将三角尺的直角顶点落在OC的任意一点P处,使三角尺的两条直角边与∠AOB的两边分别垂直,垂足分别为E,F,则PE PF.(填“>”“<”或“=”)
(2)如图2,把三角尺绕点P旋转,两直角边分别与OA,OB交于点E,F,那么PE与PF相等吗 请说明理由.
25.(12分)如图,在四边形ABCD中,AD∥BC,F是CD的中点,连接AF并延长交BC的延长线于点E.
(1)请你判断点F是否为线段AE的对称中心.
(2)求证:四边形ABCD的面积与△ABE的面积相等.
(3)若AB=AD+BC,则线段AE的垂直平分线一定经过B点,为什么
参考答案
一、选择题
1.A 【解析】 根据轴对称图形与中心对称图形的定义,可知:
选项 A B C D
轴对称图形 √ × √ ×
中心对称图形 × √ √ ×
故A项符合题意.故选A.
2.D 【解析】 如图,作射线AM,由题意得,MG=MH,MG⊥AB,MH⊥AC,∴AM平分∠BAC.故选D.
3.B 【解析】 由题意,知α==72°.故选B.
4.A
5.C
6.B 【解析】 第一个图形是轴对称图形,有1条对称轴;第二个图形是轴对称图形,有2条对称轴;第三个图形是轴对称图形,有2条对称轴;第四个图形是轴对称图形,有6条对称轴.则所有轴对称图形的对称轴条数之和为11.故选B.
7.B 【解析】 连接OC,因为点O是BC,AC的垂直平分线的交点,所以OB=OC,OC=OA,所以OA=OB=5 cm,所以△AOB的周长为OA+OB+AB=18 cm.故选B.
8.A 【解析】 ∵∠BAC=90°,∠B=50°,∴∠C=40°,∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',∴∠AB'B=∠B=50°,∴∠CAB'=∠AB'B-∠C=10°.故选A.
9.B 【解析】 ∵AB∥CD,∴∠ACD=∠BAC=25°,∵DE是AC的垂直平分线,∴DA=DC,AE=CE,易知△ADE≌△CDE,∴∠DAC=∠DCA=25°,∴∠ADC=130°.故选B.
10.C 【解析】 ∵AD是∠BAC的平分线,∴∠CAD=∠BAD,由EF垂直平分AD,易知△FAE≌△FDE,∴∠FDA=∠FAD.∵∠FDA是△ABD的一个外角,∴∠B=∠FDA-∠BAD=∠FAD-∠CAD=∠FAC=65°.故选C.
11.B 【解析】 由作图过程可知,CE平分∠ACB,CB=CD,易知△CDF≌△CBF,所以DF=BF,所以S△CDF=S△CBF,S△ADF=S△ABF,所以S△CDF +S△ADF=S△CBF+S△ABF,所以S△ACF=S△ABC=×10=5.故选B.
12.D 【解析】 如图,过点O分别作OE⊥BA交BA的延长线于点E,OF⊥AC于点F,OG⊥BC于点G.因为点O在∠ACD的平分线CO上,所以OF=OG,同理可得OG=OE,所以OE=OF,所以AO平分∠EAF,所以∠CAO=∠EAF=(180°-∠BAC)=(180°-50°)=65°.故选D.
13.D 【解析】 由题意可知DF=D1F,DA=D1A1,AE=A1E,所以阴影部分图形的周长为D1F+BE+FC+CB+D1A1+A1E=DF+BE+FC+CB+DA+AE=(DF+FC)+(BE+AE)+DA+CB=10+10+5+5=30.故选D.
14.B 【解析】 如图,过点D作DH⊥AB交BA的延长线于点H,因为BD平分∠ABC,∠BCD=90°,所以DH=CD=4,所以四边形ABCD的面积为S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.故选B.
15.C 【解析】 如图,过点O作MN,MN⊥AB于点M,交CD于点N,∵AB∥CD,∴MN⊥CD,∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,∴OM=OE=2,∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,∴ON=OE=2,∴MN=OM+ON=4,即AB与CD之间的距离是4.故选C.
16.B 【解析】 如图,分别作点A关于BC和CD的对称点A',A″,连接A'A″,交BC于点M,交CD于点N,则A'A″的长为△AMN周长的最小值.∵∠DAB=120°,∴∠AA'M+∠A″=60°.∵∠MA'A=∠MAA',∠NAD=∠A″,且∠MA'A+∠MAA'=∠AMN,∠NAD+∠A″=∠ANM,∴∠AMN+∠ANM=∠MA'A+∠MAA'+∠NAD+∠A″=2(∠AA'M+∠A″)=2×60°=120°.故选B.
二、填空题
17.钝角 【解析】 由DE垂直平分AC,易得∠DAC=∠C=15°,∴∠ADB=30°,∴∠ABD=
180°-∠BAD-∠ADB=94°,∴△ABC是钝角三角形.
18.2 【解析】 如图,作IE⊥AC于E,IF⊥BC于F,连接IA,IB,IC,∵I为△ABC各内角平分线的交点,IE⊥AC,IF⊥BC,IH⊥AB,∴IE=IF=IH,则AB·IH+AC·IE+BC·IF=BC·AC,解得 IH=2.
19.(1)1∶1; (2)m∶n; (3)9 【解析】 (1)如图1,过点A作AE⊥BC于E,∵点D是BC边上的中点,∴BD=DC,∴S△ABD∶S△ACD=(×BD×AE)∶(×CD×AE)=1∶1.(2)如图2,过点D作DE⊥AB于E,DF⊥AC于F,∵AD为∠BAC的平分线,∴DE=DF,∵AB=m,AC=n,∴S△ABD∶S△ACD=(×AB×DE)∶(×AC×DF)=m∶n,(3)∵AD=DE,∴由(1)知,S△ABD∶S△BDE=1∶1.∵S△BDE=6,∴S△ABD=6.∵AC=2,AB=4,
AD平分∠CAB,∴由(2)知,S△ABD∶S△ACD=AB∶AC=4∶2=2∶1,∴S△ACD=3,∴S△ABC=3+6=9.
三、解答题
20.【解析】 (1)①;②;④
(2)点O的位置如图所示.
(3)直线m的位置如图所示.
21.【解析】 (1)如图,BD即为所作.
(2)∵∠A=40°,∠C=60°,
∴∠ABC=180°-∠A-∠C=180°-40°-60°=80°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°,
∴∠BDC=∠A+∠ABD=40°+40°=80°.
22.【解析】 如图,连接PB,PC,
∵AP平分∠BAC,PE⊥AB,PF⊥AC,
∴PE=PF,∠PEB=∠PFC=90°,
在△BEP和△CFP中,
∴△BEP≌△CFP(SAS),
∴BP=CP,∴点P在BC的垂直平分线上.
23.【解析】 如图,连接OA,OC,
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD.
∵AB=CD,∴△ABO≌△CDO(SSS),
∴∠ABO=∠CDO.
易知△OBF≌△ODF,∴∠OBD=∠ODB.
设∠OBD=∠ODB=α,∠ABO=∠CDO=β,
∴解得
∴∠OBD=41°.
24.【解析】 (1)=
(2)PE=PF.理由如下:
如图,过点P作PM⊥OA于点M,PN⊥OB于点N,则∠PME=∠PNF=90°.
∵OP平分∠AOB,∴PM=PN.
∵∠AOB=∠PME=∠PNO=90°,
∴∠MPN=90°.
∵∠EPF=90°,∴∠MPE=∠FPN.
在△PEM和△PFN中,
∴△PEM≌△PFN(ASA),∴PE=PF.
25.【解析】 (1)∵AD∥BC,∴∠DAF=∠CEF,∠ADF=∠ECF.
∵F是CD的中点,∴DF=CF.
在△ADF和△ECF中,
∴△ADF≌△ECF(AAS).
∴AF=EF,即F是线段AE的对称中心.
(2)由(1)可知,△ADF≌△ECF,∴S△ADF=S△ECF,
∴S四边形ABCD=S四边形ABCF+S△ADF=S四边形ABCF+S△ECF=S△ABE.
(3)∵△ADF≌△ECF,∴AD=CE,
∴AB=AD+BC=CE+BC=BE,
∴点B在线段AE的垂直平分线上,即线段AE的垂直平分线经过B点.
作答时间:120分钟 总分:120分
一、选择题(本大题有16个小题,每小题3分,共48分)
1.下列图形中,是轴对称图形,但不是中心对称图形的是 ( )
2.已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,则点M一定在 ( )
A.AC边的高上
B.AB边的中线上
C.BC边的垂直平分线上
D.∠A的平分线上
3.利用图形的旋转可以设计出许多美丽的图案.如图2中的图案是由图1所示的基本图案以点O为旋转中心,顺时针(或逆时针)连续旋转,每次旋转α角构成,则α为 ( )
A.36° B.72° C.144° D.216°
4.剪纸是我国传统的民间艺术.将一张纸片按图①,②中的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是 ( )
5.从平面镜里看到背后墙上电子钟的示数如图所示,这时的正确时间是 ( )
A.20:12 B.20:15 C.21:05 D.21:15
6.下列图形中,所有轴对称图形的对称轴条数之和为 ( )
A.13 B.11 C.10 D.8
7.如图,在△ABC中,点O是BC,AC的垂直平分线的交点,OB=5 cm,AB=8 cm,则△AOB的周长为 ( )
A.21 cm B.18 cm C.15 cm D.13 cm
8.如图,在直角三角形ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为 ( )
A.10° B.20° C.30° D.40°
9.如图,DE是AC的垂直平分线,AB∥CD.若∠BAC=25°,则∠ADC的度数是 ( )
A.120° B.130° C.140° D.150°
10.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为 ( )
A.45° B.50° C.65° D.60°
11.如图,在△ABC中,嘉淇同学按以下步骤作图:①以点C为圆心,以BC的长为半径画弧,交AC于点D,连接BD;②分别以点B,D为圆心,以大于BD的长为半径画弧,两弧交于点E;③作射线CE交BD于点F,连接AF.
若△ABC的面积为10,则△ACF的面积为 ( )
A.2.5 B.5 C.7.5 D.8
12.如图,△ABC的外角∠ACD的平分线CO与∠ABC的平分线BO相交于点O,连接OA.若∠BAC=50°,则∠CAO的度数为 ( )
A.50° B.55° C.60° D.65°
13.如图,在长方形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠,使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为 ( )
A.15 B.20 C.25 D.30
14.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是 ( )
A.24 B.30 C.36 D.42
15.如图,AB∥CD,O为∠BAC,∠ACD的平分线的交点,OE⊥AC于点E.若OE=2,则AB与CD之间的距离是 ( )
A.8 B.6 C.4 D.2
16.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,分别在BC,CD上找一点M,N,使△AMN周长最小时,∠AMN+∠ANM的度数为 ( )
A.130° B.120° C.110° D.100°
二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)
17.如图,△ABC中,DE垂直平分AC,与AC交于点E,与BC交于点D,∠C=15°,∠BAD=56°,则△ABC的形状是 三角形.(填“锐角”“直角”或“钝角”)
18.如图,已知△ABC中,∠ACB=90°,点I为△ABC各内角平分线的交点,过点I作AB的垂线,垂足为H.若BC=6,AC=8,AB=10,则IH= .
19.在△ABC中,D是BC边上的点(不与点B,C重合),连接AD.
(1)如图1,当D是BC边上的中点时,S△ABD∶S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,S△ABD∶S△ACD= (用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
三、解答题(本大题有6个小题,共60分)
20.(8分)如图,甲和乙是全等图形,但两个四边形的顶点字母不同.
(1)请从下列序号中选择正确选项的序号填写:①点E,F,G,H;②点G,F,E,H;③点E,H,G,F;④点G,H,E,F.
如果甲经过一次平移后得到乙,那么点A,B,C,D的对应点依次为 ;
如果甲经过一次轴对称后得到乙,那么点A,B,C,D的对应点依次为 ;
如果甲经过中心对称后得到乙,那么点A,B,C,D的对应点依次为 .
(2)如果甲与乙关于O点成中心对称,请画出对称中心.(保留作图痕迹,不写作法)
(3)如果甲与乙关于直线m成轴对称,请你利用尺规作图画出直线m.(保留作图痕迹,不写作法)
21.(9分)如图,在△ABC中,∠A=40°,∠C=60°.
(1)用直尺和圆规作∠ABC的平分线,交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求∠BDC的度数.
22.(10分)如图,在△ABC中,AP平分∠BAC,PE⊥AB于点E,PF⊥AC交AC的延长线于点F,BE=CF.求证:点P在BC的垂直平分线上.
23.(10分)如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
24.(11分)已知∠AOB=90°,OC为∠AOB的平分线.
(1)如图1,将三角尺的直角顶点落在OC的任意一点P处,使三角尺的两条直角边与∠AOB的两边分别垂直,垂足分别为E,F,则PE PF.(填“>”“<”或“=”)
(2)如图2,把三角尺绕点P旋转,两直角边分别与OA,OB交于点E,F,那么PE与PF相等吗 请说明理由.
25.(12分)如图,在四边形ABCD中,AD∥BC,F是CD的中点,连接AF并延长交BC的延长线于点E.
(1)请你判断点F是否为线段AE的对称中心.
(2)求证:四边形ABCD的面积与△ABE的面积相等.
(3)若AB=AD+BC,则线段AE的垂直平分线一定经过B点,为什么
参考答案
一、选择题
1.A 【解析】 根据轴对称图形与中心对称图形的定义,可知:
选项 A B C D
轴对称图形 √ × √ ×
中心对称图形 × √ √ ×
故A项符合题意.故选A.
2.D 【解析】 如图,作射线AM,由题意得,MG=MH,MG⊥AB,MH⊥AC,∴AM平分∠BAC.故选D.
3.B 【解析】 由题意,知α==72°.故选B.
4.A
5.C
6.B 【解析】 第一个图形是轴对称图形,有1条对称轴;第二个图形是轴对称图形,有2条对称轴;第三个图形是轴对称图形,有2条对称轴;第四个图形是轴对称图形,有6条对称轴.则所有轴对称图形的对称轴条数之和为11.故选B.
7.B 【解析】 连接OC,因为点O是BC,AC的垂直平分线的交点,所以OB=OC,OC=OA,所以OA=OB=5 cm,所以△AOB的周长为OA+OB+AB=18 cm.故选B.
8.A 【解析】 ∵∠BAC=90°,∠B=50°,∴∠C=40°,∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',∴∠AB'B=∠B=50°,∴∠CAB'=∠AB'B-∠C=10°.故选A.
9.B 【解析】 ∵AB∥CD,∴∠ACD=∠BAC=25°,∵DE是AC的垂直平分线,∴DA=DC,AE=CE,易知△ADE≌△CDE,∴∠DAC=∠DCA=25°,∴∠ADC=130°.故选B.
10.C 【解析】 ∵AD是∠BAC的平分线,∴∠CAD=∠BAD,由EF垂直平分AD,易知△FAE≌△FDE,∴∠FDA=∠FAD.∵∠FDA是△ABD的一个外角,∴∠B=∠FDA-∠BAD=∠FAD-∠CAD=∠FAC=65°.故选C.
11.B 【解析】 由作图过程可知,CE平分∠ACB,CB=CD,易知△CDF≌△CBF,所以DF=BF,所以S△CDF=S△CBF,S△ADF=S△ABF,所以S△CDF +S△ADF=S△CBF+S△ABF,所以S△ACF=S△ABC=×10=5.故选B.
12.D 【解析】 如图,过点O分别作OE⊥BA交BA的延长线于点E,OF⊥AC于点F,OG⊥BC于点G.因为点O在∠ACD的平分线CO上,所以OF=OG,同理可得OG=OE,所以OE=OF,所以AO平分∠EAF,所以∠CAO=∠EAF=(180°-∠BAC)=(180°-50°)=65°.故选D.
13.D 【解析】 由题意可知DF=D1F,DA=D1A1,AE=A1E,所以阴影部分图形的周长为D1F+BE+FC+CB+D1A1+A1E=DF+BE+FC+CB+DA+AE=(DF+FC)+(BE+AE)+DA+CB=10+10+5+5=30.故选D.
14.B 【解析】 如图,过点D作DH⊥AB交BA的延长线于点H,因为BD平分∠ABC,∠BCD=90°,所以DH=CD=4,所以四边形ABCD的面积为S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.故选B.
15.C 【解析】 如图,过点O作MN,MN⊥AB于点M,交CD于点N,∵AB∥CD,∴MN⊥CD,∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,∴OM=OE=2,∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,∴ON=OE=2,∴MN=OM+ON=4,即AB与CD之间的距离是4.故选C.
16.B 【解析】 如图,分别作点A关于BC和CD的对称点A',A″,连接A'A″,交BC于点M,交CD于点N,则A'A″的长为△AMN周长的最小值.∵∠DAB=120°,∴∠AA'M+∠A″=60°.∵∠MA'A=∠MAA',∠NAD=∠A″,且∠MA'A+∠MAA'=∠AMN,∠NAD+∠A″=∠ANM,∴∠AMN+∠ANM=∠MA'A+∠MAA'+∠NAD+∠A″=2(∠AA'M+∠A″)=2×60°=120°.故选B.
二、填空题
17.钝角 【解析】 由DE垂直平分AC,易得∠DAC=∠C=15°,∴∠ADB=30°,∴∠ABD=
180°-∠BAD-∠ADB=94°,∴△ABC是钝角三角形.
18.2 【解析】 如图,作IE⊥AC于E,IF⊥BC于F,连接IA,IB,IC,∵I为△ABC各内角平分线的交点,IE⊥AC,IF⊥BC,IH⊥AB,∴IE=IF=IH,则AB·IH+AC·IE+BC·IF=BC·AC,解得 IH=2.
19.(1)1∶1; (2)m∶n; (3)9 【解析】 (1)如图1,过点A作AE⊥BC于E,∵点D是BC边上的中点,∴BD=DC,∴S△ABD∶S△ACD=(×BD×AE)∶(×CD×AE)=1∶1.(2)如图2,过点D作DE⊥AB于E,DF⊥AC于F,∵AD为∠BAC的平分线,∴DE=DF,∵AB=m,AC=n,∴S△ABD∶S△ACD=(×AB×DE)∶(×AC×DF)=m∶n,(3)∵AD=DE,∴由(1)知,S△ABD∶S△BDE=1∶1.∵S△BDE=6,∴S△ABD=6.∵AC=2,AB=4,
AD平分∠CAB,∴由(2)知,S△ABD∶S△ACD=AB∶AC=4∶2=2∶1,∴S△ACD=3,∴S△ABC=3+6=9.
三、解答题
20.【解析】 (1)①;②;④
(2)点O的位置如图所示.
(3)直线m的位置如图所示.
21.【解析】 (1)如图,BD即为所作.
(2)∵∠A=40°,∠C=60°,
∴∠ABC=180°-∠A-∠C=180°-40°-60°=80°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°,
∴∠BDC=∠A+∠ABD=40°+40°=80°.
22.【解析】 如图,连接PB,PC,
∵AP平分∠BAC,PE⊥AB,PF⊥AC,
∴PE=PF,∠PEB=∠PFC=90°,
在△BEP和△CFP中,
∴△BEP≌△CFP(SAS),
∴BP=CP,∴点P在BC的垂直平分线上.
23.【解析】 如图,连接OA,OC,
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD.
∵AB=CD,∴△ABO≌△CDO(SSS),
∴∠ABO=∠CDO.
易知△OBF≌△ODF,∴∠OBD=∠ODB.
设∠OBD=∠ODB=α,∠ABO=∠CDO=β,
∴解得
∴∠OBD=41°.
24.【解析】 (1)=
(2)PE=PF.理由如下:
如图,过点P作PM⊥OA于点M,PN⊥OB于点N,则∠PME=∠PNF=90°.
∵OP平分∠AOB,∴PM=PN.
∵∠AOB=∠PME=∠PNO=90°,
∴∠MPN=90°.
∵∠EPF=90°,∴∠MPE=∠FPN.
在△PEM和△PFN中,
∴△PEM≌△PFN(ASA),∴PE=PF.
25.【解析】 (1)∵AD∥BC,∴∠DAF=∠CEF,∠ADF=∠ECF.
∵F是CD的中点,∴DF=CF.
在△ADF和△ECF中,
∴△ADF≌△ECF(AAS).
∴AF=EF,即F是线段AE的对称中心.
(2)由(1)可知,△ADF≌△ECF,∴S△ADF=S△ECF,
∴S四边形ABCD=S四边形ABCF+S△ADF=S四边形ABCF+S△ECF=S△ABE.
(3)∵△ADF≌△ECF,∴AD=CE,
∴AB=AD+BC=CE+BC=BE,
∴点B在线段AE的垂直平分线上,即线段AE的垂直平分线经过B点.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
