人教版八年级数学上册 12.2 三角形全等的判定 第1课时 SSS(课件)(共24张PPT)
文档属性
| 名称 | 人教版八年级数学上册 12.2 三角形全等的判定 第1课时 SSS(课件)(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 13:17:19 | ||
图片预览






文档简介
(共24张PPT)
第1课时 SSS
12.2 三角形全等的判定
学习目标
1.能自己试验探索出判定三角形全等的条件:边边边公理.
2.会应用判定方法SSS进行简单的推理判定两个三角形全等.
3.会作一个角等于已知角.
新课导入
壹
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗?
课堂导入
讲授新知
贰
如果△ABC≌△A'B'C',则有对应边相等,对应角相等.反之,根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,那么△ABC和△A'B'C'能够完全重合,即判定△ABC≌△A'B'C'.
如果只选取其中的一部分条件还能保证两个三角形全等吗?
知识点1 全等三角形判定1
讲授新知
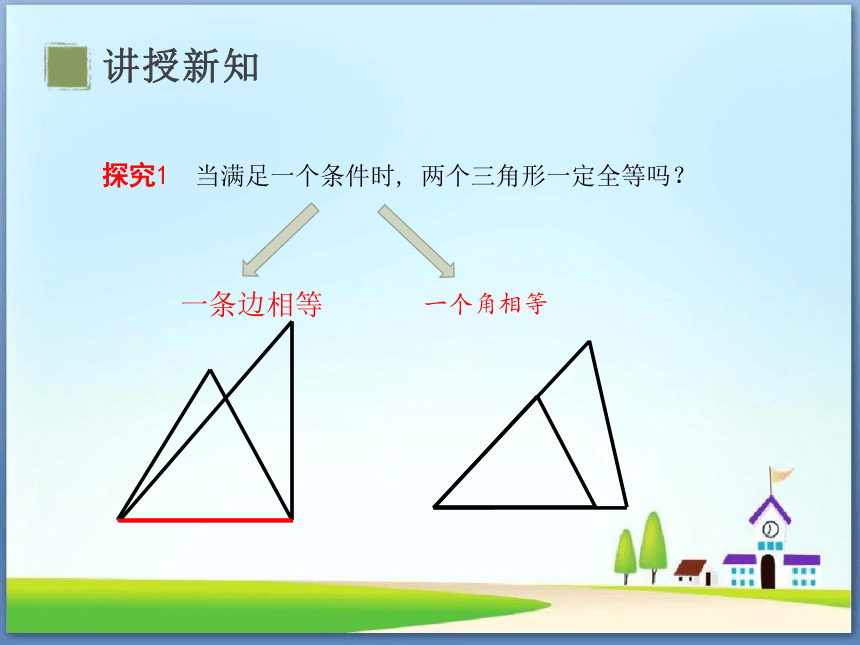
探究1 当满足一个条件时, 两个三角形一定全等吗?
一条边相等
一个角相等
讲授新知
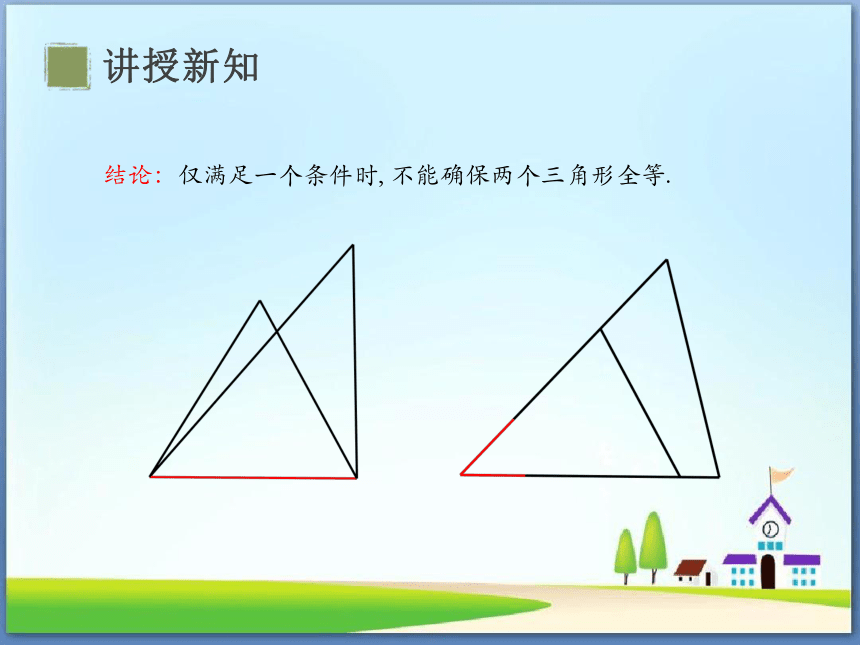
结论:仅满足一个条件时, 不能确保两个三角形全等.
讲授新知
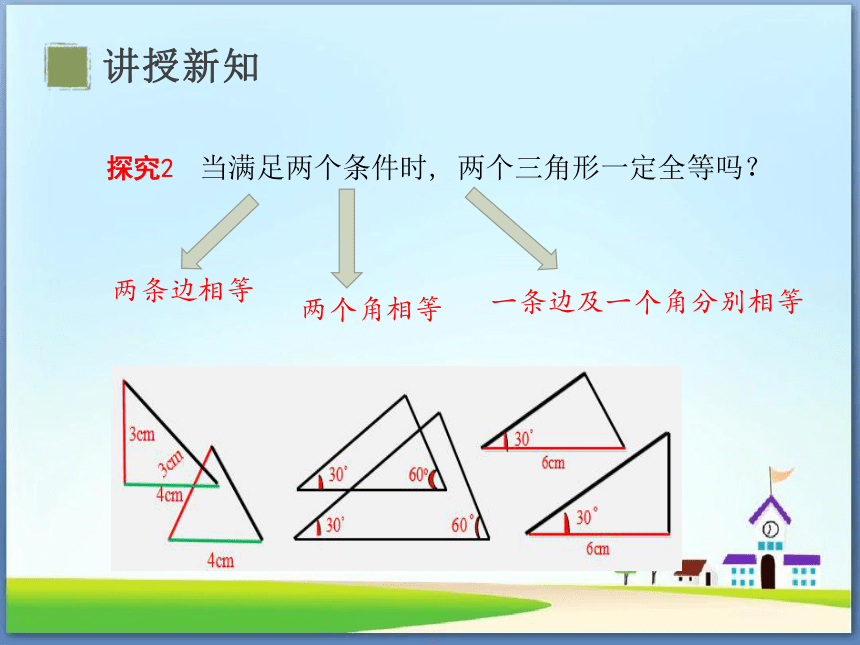
探究2 当满足两个条件时, 两个三角形一定全等吗?
两条边相等
两个角相等
一条边及一个角分别相等
讲授新知
结论:当满足两个条件时, 也不能确保两个三角形全等.
讲授新知
探究3 当满足三个条件时, 两个三角形一定全等吗?
① 三角
② 三边
③ 两边一角
④ 两角一边
三个条件
×
?
讲授新知
先任意画出一个△ABC,再画出一个△A′B′C′ ,使
A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,他们全等吗?
作图探究
A
B
C
A ′
B′
C′
想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
作法:
(1)画B′C′=BC;
(2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A';
(3)连接线段A'B',A 'C '.
讲授新知
判定1:三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
所以△ABC≌△A'B'C'.(SSS)
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
讲授新知
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证:△ABD≌△ACD.
证明:因为点D是BC的中点,所以BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
所以△ABD≌△ACD(SSS).
A
B
C
D
AD 称为公共边.
范例应用
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例2 用尺规作一个角等于已知角.
O
D
B
C
A
O′
C′
A′
B′
D ′
范例应用
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
范例应用
例3 工人师傅常用角尺平分一个任意角.做法如下:
如图所示,∠AOB是一个任意角,在边OA,OB上分别截取OM=ON.移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
解:在△MOC和△NOC中,
所以△MOC≌△NOC(SSS).
所以∠MOC=∠NOC,所以OC是∠AOB的平分线.
A
M
C
N
B
O
OM=ON,
OC=OC,
CM=CN,
范例应用
当堂训练
叁
解: △ABC≌△DCB.理由如下:
在△ABC和△DCB,
AB = DC,
AC = DB,
= ,
BC
CB
△DCB
A
B
C
D
所以△ABC ≌ ( ).
SSS
1.如图所示,AB=CD,AC=BD,△ABC和△DCB是否全等?请完成下列解题步骤.
=
=
2.如图所示,D、F是线段BC上的两点,AB=CE,AF=DE,要使△ABF≌△ECD ,还需要条件 .
BF=CD
或 BD=FC
A
E
=
=
×
×
B
D
F
C
当堂训练
3.如图所示,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)因为 AD=FB,
所以AB=FD(等式性质).
在△ABC和△FDE 中,
AC=FE(已知),
BC=DE(已知),
AB=FD(已证),
所以△ABC≌△FDE(SSS);
A
C
E
D
B
F
=
=
。
。
(2)因为 △ABC≌△FDE(已证).
所以 ∠C=∠E(全等三角形的对应角相等).
当堂训练
课堂小结
肆
三角形全等的判定
三边分别相等的两个三角形全等
SSS
尺规作图
作一个角等于已知角
应用
利用“SSS”解决实际问题
分类探讨
只满足一个条件或者两个条件时不能判定三角形全等
课堂小结
课后作业
课后习题 P37第 1,2题。
谢
谢
第1课时 SSS
12.2 三角形全等的判定
学习目标
1.能自己试验探索出判定三角形全等的条件:边边边公理.
2.会应用判定方法SSS进行简单的推理判定两个三角形全等.
3.会作一个角等于已知角.
新课导入
壹
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗?
课堂导入
讲授新知
贰
如果△ABC≌△A'B'C',则有对应边相等,对应角相等.反之,根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,那么△ABC和△A'B'C'能够完全重合,即判定△ABC≌△A'B'C'.
如果只选取其中的一部分条件还能保证两个三角形全等吗?
知识点1 全等三角形判定1
讲授新知
探究1 当满足一个条件时, 两个三角形一定全等吗?
一条边相等
一个角相等
讲授新知
结论:仅满足一个条件时, 不能确保两个三角形全等.
讲授新知
探究2 当满足两个条件时, 两个三角形一定全等吗?
两条边相等
两个角相等
一条边及一个角分别相等
讲授新知
结论:当满足两个条件时, 也不能确保两个三角形全等.
讲授新知
探究3 当满足三个条件时, 两个三角形一定全等吗?
① 三角
② 三边
③ 两边一角
④ 两角一边
三个条件
×
?
讲授新知
先任意画出一个△ABC,再画出一个△A′B′C′ ,使
A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,他们全等吗?
作图探究
A
B
C
A ′
B′
C′
想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
作法:
(1)画B′C′=BC;
(2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A';
(3)连接线段A'B',A 'C '.
讲授新知
判定1:三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
所以△ABC≌△A'B'C'.(SSS)
现象:两个三角形放在一起能完全重合.
说明:这两个三角形全等.
讲授新知
例1 在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.求证:△ABD≌△ACD.
证明:因为点D是BC的中点,所以BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
所以△ABD≌△ACD(SSS).
A
B
C
D
AD 称为公共边.
范例应用
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
例2 用尺规作一个角等于已知角.
O
D
B
C
A
O′
C′
A′
B′
D ′
范例应用
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步中
所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
范例应用
例3 工人师傅常用角尺平分一个任意角.做法如下:
如图所示,∠AOB是一个任意角,在边OA,OB上分别截取OM=ON.移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
解:在△MOC和△NOC中,
所以△MOC≌△NOC(SSS).
所以∠MOC=∠NOC,所以OC是∠AOB的平分线.
A
M
C
N
B
O
OM=ON,
OC=OC,
CM=CN,
范例应用
当堂训练
叁
解: △ABC≌△DCB.理由如下:
在△ABC和△DCB,
AB = DC,
AC = DB,
= ,
BC
CB
△DCB
A
B
C
D
所以△ABC ≌ ( ).
SSS
1.如图所示,AB=CD,AC=BD,△ABC和△DCB是否全等?请完成下列解题步骤.
=
=
2.如图所示,D、F是线段BC上的两点,AB=CE,AF=DE,要使△ABF≌△ECD ,还需要条件 .
BF=CD
或 BD=FC
A
E
=
=
×
×
B
D
F
C
当堂训练
3.如图所示,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)因为 AD=FB,
所以AB=FD(等式性质).
在△ABC和△FDE 中,
AC=FE(已知),
BC=DE(已知),
AB=FD(已证),
所以△ABC≌△FDE(SSS);
A
C
E
D
B
F
=
=
。
。
(2)因为 △ABC≌△FDE(已证).
所以 ∠C=∠E(全等三角形的对应角相等).
当堂训练
课堂小结
肆
三角形全等的判定
三边分别相等的两个三角形全等
SSS
尺规作图
作一个角等于已知角
应用
利用“SSS”解决实际问题
分类探讨
只满足一个条件或者两个条件时不能判定三角形全等
课堂小结
课后作业
课后习题 P37第 1,2题。
谢
谢
