公式法课件

课件43张PPT。第三节 公式法分解因式平方差公式分解因式1、把一个多项式化为几个 的 的形式,就是因式分解.2、把下列各式分解因式。（1）4x3-6x2
（2） 2x3y3_2x2y2+3xy
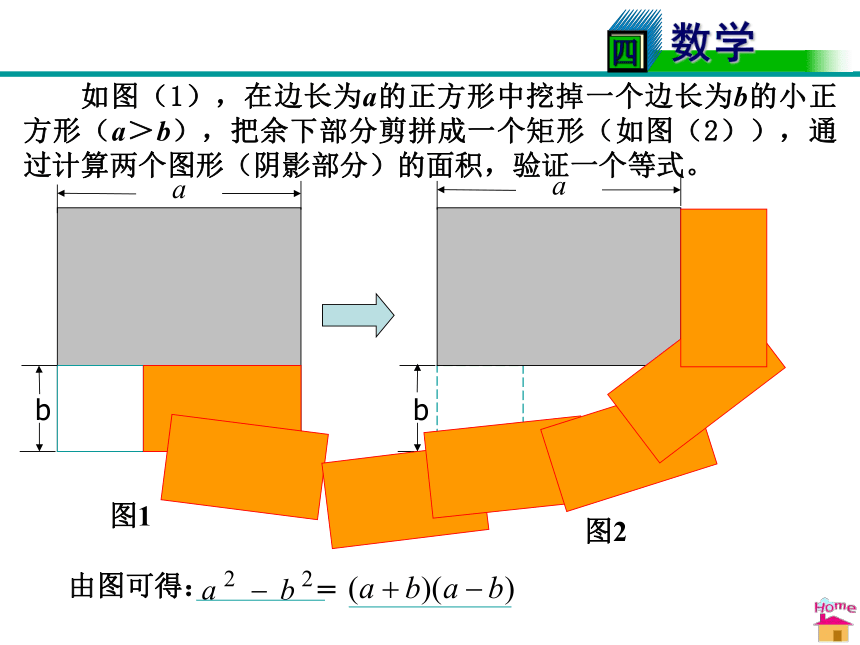
（3）-6m2n-15mn2+30m2n2 （4）6m(p-3)+12n(3-p)复习回顾 如图（1），在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下部分剪拼成一个矩形（如图（2）），通过计算两个图形（阴影部分）的面积，验证一个等式。 也就是说，两个数的平方差，等于这两个数的和与它们的差的积。 利用这整式乘法与因式分解过程相反的关系，我们把乘法公式反过来，就可以用来把某些多项式分解因式，这种方法叫运用公式法。新知识点实例探究3x2y【例1 】把下列各式分解因式.⒊利用平方差公式把下列各式分解因式 ×× 学校搞美化工程，在一个边长为a=118.5米的正方形广场的四角均留出一个边长为b=9.25米的正方形修建花坛，其余地方种草坪。
（1）草坪的面积有多大?解：（1）广场种草坪的面积为：当a=118.5，b=9.25时生活实践生活实践 学校搞美化工程，在一个边长为a=118.5米的正方形广场的四角均留出一个边长为b=9.25米的正方形修建花坛，其余地方种草坪。（2）如果草坪每平方米需5元，那么给这个广场种草坪，至少投资多少钱？答： （1）草坪的面积是13700平方米；
（2）至少投资68500元。 如图，在半径为R的圆形钢板上，冲去半径为r的四个小圆，利用因式分解计算当R=7.8cm，r=1.1cm时，剩余部分的面积。（π取3.14，结果保留三位有效数字 ）当R=7.8cm，r=1.1cm时答：剩余部分的面积约为176cm2 。应用例题精讲1、把下列各式分解因式:(1) 36-25x2解：(1) 36-25x2=62-(5x)2=(6+5x)(6-5x)(2) 16a2-9b2(2) 16a2-9b2=(4a)2-(3b)2=(4a+3b)(4a-3b)2、把多项式9(a+b)2-4(a-b)2分解因式.解：9(a+b)2-4(a-b)2=[3(a+b)]2-[2(a-b)]2=[3(a+b)+2(a-b)][3(a+b)-2(a-b)]=(3a+3b+2a-2b)(3a+3b-2a+2b)=(5a+b)(a+5b)★平方差公式中字母a、b不仅可以表示数，而且也可以表示其它代数式.3、把多项式x4-16分解因式.解：x4-16=(x2)2-42=(x2+4)(x2-4)★分解因式应分解到各因式都不能再分解为止.=(x2+4)(x+2)(x-2)★若多项式中有公因式,应先提取公因式,然后再进一步分解因式,直到不能分解为止.解：2x3-8x4、把多项式2x3-8x分解因式.=2x (x2_22) =2x (x+2)(x-2)=2x (x2-4)5、把下列各式分解因式:(1) a4–b4=(2) (m2-3)2–1=(a2)2-(b2)2=(a2+b2)(a2-b2)=(a2+b2)(a+b)(a-b)(m2-3-1)(m2-3+1)=(m2-4)(m2-2)=(m+2)(m-2)(m2-2)课堂小结1.平方差公式： a2-b2 = (a+b)(a-b)2.用平方差公式因式分解步骤：
一变、二分解知识点二：完全平方分解因式提取公因式法：ma+mb+mc=m(a+b+c)
运用公式法： ① a2-b2=(a+b)(a-b)
练习把下列各式分解因式① ② x4-16解:原式=ax2(x2-1)
=ax2(x+1)(x-1)解:原式=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2)课前复习：1、分解因式学了哪些方法（有公因式，先提公因式。）（因式分解要彻底。）课前复习：2．除了平方差公式外，还学过了哪些公式？ 用公式法正确分解因式关键是什么？熟知公式特征！完全平方式从项数看：完全平方式都有两项可化为两个数(或整式)的平方,另一项为这两个数(或整式)的乘积的2倍.从符号看：平方项符号相同a2 ± 2 a b + b2 = （ a ± b ）2 （即：两平方项的符号同号，首尾2倍中间项）
是a表示2y，
b表示1否否否是a表示2y，
b表示3x是a表示(a+b)，
b表示1多项式是a表示x，
b表示3
否否是a表示 ，
b表示3n多项式是a表示x，
b表示1/2
填空： （1）a2+ +b2=(a+b)2 （2）a2-2ab+ =(a-b) 2 （3）m2+2m+ =( ) 2 （4）n2-2n+ =( ) 2（5）x2-x+0.25=( ) 2 （6）4x2+4xy+( ) 2=( ) 22abb21m+11n-1x-0.5y2x+y(1)x2＋14x＋49 解：(2)解：例题1 (3)3ax2＋6axy＋3ay2 解：(4)解： -x2-4y2＋4xy 解：(5)解： 16x4-8x2＋1（6）解：（1）25x2＋10x＋1 解:原式=（5x)2+2×5x×1+12
=(5x+1)2解:原式=（3a)2-2×3a×b+b2
=(3a-b)2因式分解解:原式=（7a)2+2×7a×b+b2
=(7a+b)2 （4）-a2-10a -25解:原式=-（a2+2×a×5+52)

=-(a+5)2（5）-a3b3+2a2b3-ab3解：原式=-ab3(a2-2a×1+12)
=-ab3(a-1)2 （6）9 - 12(a-b) + 4 (a-b)2解:原式=32-2×3×2(a-b)+
=
=(3-2a+2b)2总结与反思：1:整式乘法的完全平方公式是：
2:利用完全平方公式分解因式的公式形式是：
3:完全平方公式特点：含有三项；两平方项的符号同号；首尾2倍中间项
1.已知 4x2+kxy+9y2 是一个完全平式，则k=
a2+b2
22.已知 a(a+1)-(a2-b)=-2, 求 +ab
的值。±12解: 由a(a+1)-(a2-b)=a2+a-a2+b=a+b=-2得
3.已知x2+4x+y2-2y+5=0,求 x-y 的值。解：由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1)
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴x-y=(-2)-1=4、把下列各式因式分解(7)(a+1)2-2(a2-1) ＋(a-1)2=(a+1-a+1)2=49、 (y2 + x2 )2 - 4x2y2=(y+x)2(y-x)210、简便计算：解：原式=（56+34）2=902=8100知识点三：十字交叉相乘法1.(x+2)(x+1)=x2+3x+23.(x-2)(x+1)=x2-x-24.(x-2)(x-1)=x2-3x+22.(x+2)(x-1)=x2+x-25.(x+2)(x+3)=x2+5x+66.(x+2)(x-3)=x2-x-67.(x-2)(x+3)=x2+x-68.(x-2)(x-3)=x2-5x+6(x+a)(x+b)=x2+(a+b)x+ab请直接口答计算结果：利用十字交叉线来分解系数，把二次三项式分解因式的方法叫做十字相乘法.1.x2+8x+12=2.x2-11x-12=练一练3.x2-7x+12=4.x2-4x-12=(x+2)(x+6)(x-6)(x+2)(x-3)(x-4)(x-12)(x+1)符号规律：
常数项是正数时，应分解为两个 因数，他们的符号与一次项系数符号 ；
常数项是负数时，应分解为两个 因数，其绝对值 的因数与一次项系数的符号相同.同号相同异号较大5.x2+13x+12=(x+1)(x+12)6.x2-x-12=(x-4)(x+3)将下列各式因式分解:x2+px+q=x2+(a+b)x+ab=xxabax+bx=(a+b)x(x+a)(x+b)课堂小结对二次三项式x2+px+q进行因式分解，应重点掌握以下三个问题：1.掌握方法：拆分常数项，验证一次项. 2.符号规律：
当q>0时，a、b同号，且a、b的符号与p的符号相同；
当q<0时，a、b异号，且绝对值较大的因数与p的符号相同. 3.书写格式：竖分横积(x+2)(x-3)1.x2-x- 6 =(x-3)(x+5)2.x2+2x-15=(x+2)(x-5)3.x2-3x-10=(x-5)(x-4)4.x2-9x+20=(x-7)(x+4)5.x2-3x-28=(x+2)(x-4)6.x2-2x-8=(x-1)(x-3)7.x2-4x+3=(x+3)(x+4)(x+2)(x+3)(x-3)(x+7)8.x2+7x+12=9.x2+5x+6=10.x2+4x-21=(y+12)(y-3)11.y2+9y-36=(y-9)(y+14)(y+4)(y-15)(y-7)(y+16)(y-8)(y-17)(y+16)(y+3)(y+19)(y-7)(y+11)(y-10)(y-13)(y-3)(y+14)(y+4)13.y2-11y-60=12.y2+5y-126=14.y2+9y-112=15.y2-25y+136=16.y2+19y+48=17.y2+12y-133=18.y2+y-110=19.y2-16y+39=20.y2+18y+56=