5.2.2 圆心角的度数与它所对弧的度数的关系同步练习(含答案)
文档属性
| 名称 | 5.2.2 圆心角的度数与它所对弧的度数的关系同步练习(含答案) | 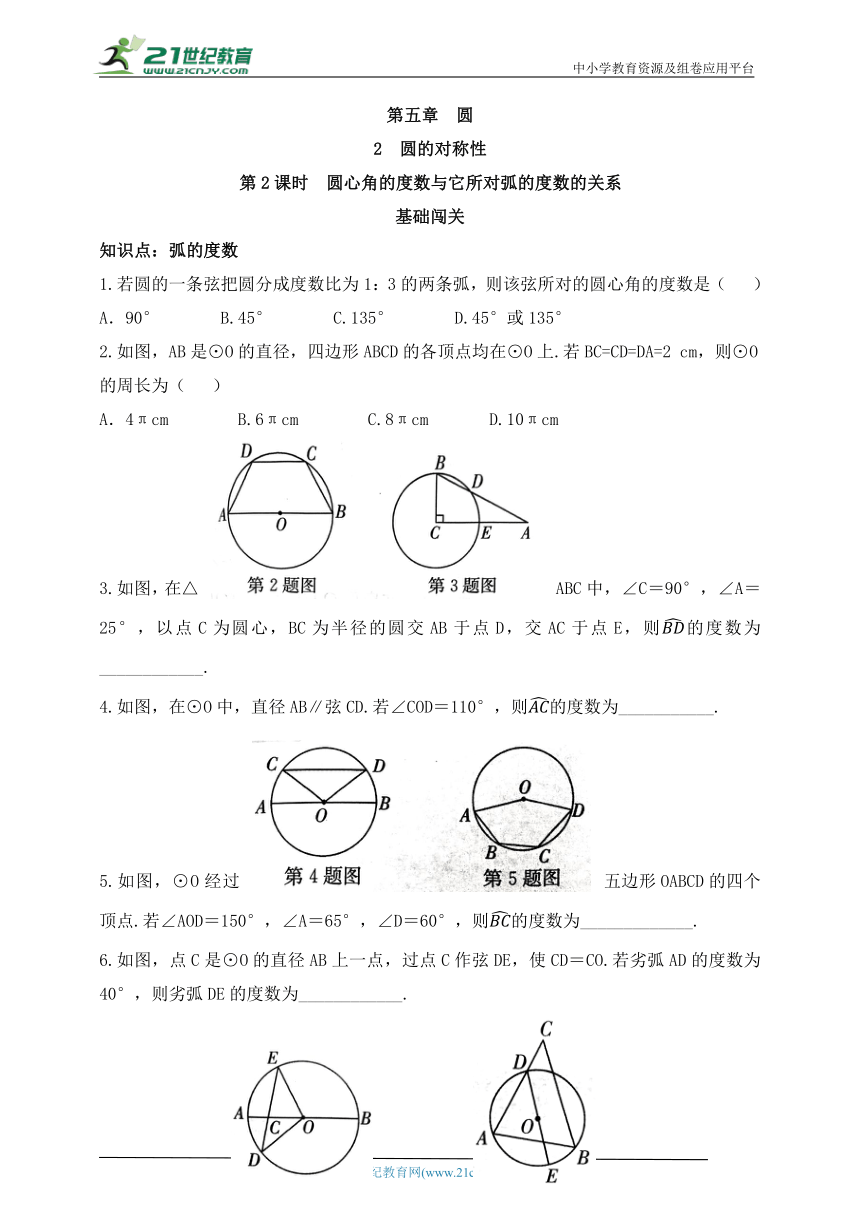 | |
| 格式 | docx | ||
| 文件大小 | 13.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 11:34:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
2 圆的对称性
第2课时 圆心角的度数与它所对弧的度数的关系
基础闯关
知识点:弧的度数
1.若圆的一条弦把圆分成度数比为1:3的两条弧,则该弦所对的圆心角的度数是( )
A.90° B.45° C.135° D.45°或135°
2.如图,AB是⊙O的直径,四边形ABCD的各顶点均在⊙O上.若BC=CD=DA=2 cm,则⊙O的周长为( )
A.4πcm B.6πcm C.8πcm D.10πcm
3.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为____________.
4.如图,在⊙O中,直径AB∥弦CD.若∠COD=110°,则的度数为___________.
5.如图,⊙O经过五边形OABCD的四个顶点.若∠AOD=150°,∠A=65°,∠D=60°,则的度数为_____________.
6.如图,点C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO.若劣弧AD的度数为40°,则劣弧DE的度数为____________.
第6题图 第7题图
能力提升
7.如图,△ABC的两顶点A,B在⊙O上,点C在圆外,∠C=46°,边AC交⊙O于点D,DE∥BC且经过圆心交⊙O于点E,则的度数为( )
A.46° B.92° C.88° D.44°
8.如图,将大小不同的两个量角器的0°刻度线对齐,且小量角器的中心O2恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.45° B.55° C.56° D.57°
9.如图,将△AOB绕点A顺时针旋转得到△ACD,使得点C,D都在⊙O上,且点C在BO的延长线上,则旋转角的度数为____________.
10.如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为___________.
素养提升
【模型意识——平行线与直径所夹的弧】
11.如图,已知AB是⊙O的直径,弦AC//OD.求证:=.
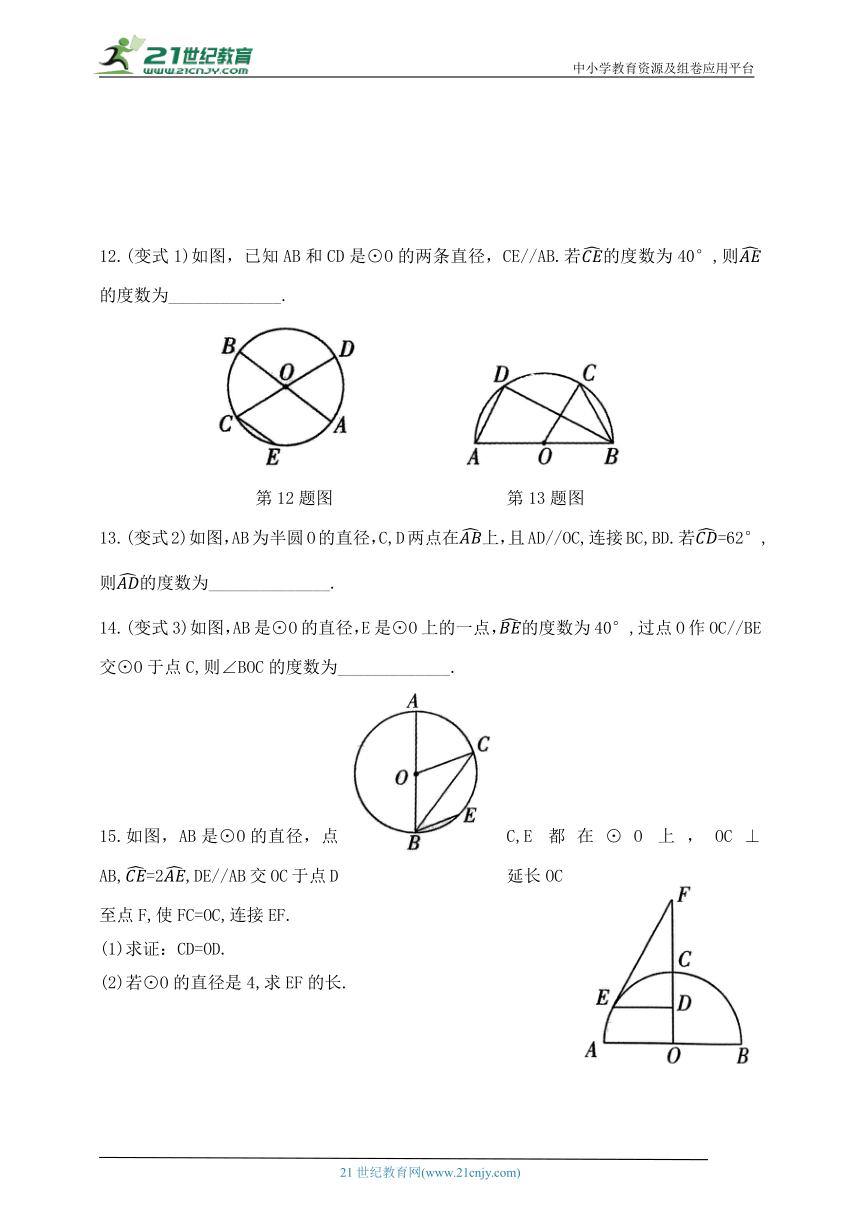
12.(变式1)如图,已知AB和CD是⊙O的两条直径,CE//AB.若的度数为40°,则的度数为_____________.
第12题图 第13题图
13.(变式2)如图,AB为半圆O的直径,C,D两点在上,且AD//OC,连接BC,BD.若=62°,则的度数为______________.
14.(变式3)如图,AB是⊙O的直径,E是⊙O上的一点,的度数为40°,过点O作OC//BE交⊙O于点C,则∠BOC的度数为_____________.
15.如图,AB是⊙O的直径,点C,E都在⊙O上,OC⊥AB,=2,DE//AB交OC于点D,延长OC至点F,使FC=OC,连接EF.
(1)求证:CD=OD.
(2)若⊙O的直径是4,求EF的长.
培优创新
16.[推理能力]如图,在扇形OAB中,∠AOB=120°,半径OA=6,C是弧AB的中点,CD⊥OA,交AB于点D,求CD的长.
参考答案
1.A 2.A 3.50° 4.35° 5.40°
6.120°[解析]∵劣弧AD的度数为40°,∴∠AOD=40°,CD=CO,∴ZD=ZCOD=40°,∴ZECO=2∠D=80°.∵OE=OD,∴ZE=ZD=40°,∴∠BOE=∠E+∠ECO=40°+80°=120°,∴劣弧BE的度数为120°。
7.C
8.A[解析]如图,连接O P,O P.∵P在小量角器上对应的刻度为63°,即ZO O P=63°,而O P=O O ,∴∠O PO =∠O O P=63°,∴∠PO O =180°-63°-63°=54°,即点P在大量角器上对应的刻度为54°.
9.60°
10.50°[解析]如图,连接OD.由题可知BC垂直平分OD,∴BD=B0.
∵OB=OD∴BD=BO=DO,∴△OBD为等边三角形,∴∠DOB=60°,∴/AOD=∠AOB-∠DOB=110°-60°=50°,∴的度数为50°。
11.证明:连接OC.∵OA=OC,∴∠OAC=∠ACO. ∵AC//OD,∴∠OAC=∠BOD,∠DOC=∠ACO,
∴∠BOD=∠COD,∴BD=CD.
12.70° 13.56°
14.110° [解析]连接OE.∵的度数为40°,∴∠BOE=40°.
∵OB=OE ,∴∠OBF=∠OEB=(180°-40)÷2=70°.∵OC//BE,∴∠BCO=∠CBE.
∵CO=BO,∴∠OBC=∠C ,∴∠CRF =∠OCB =∠OBC=∠OBE=35°,
∴∠BOC=180°-∠OBC-∠OCB=110°.
15.(1)证明:如图,连接OE,CE.∵OC⊥AB,∴∠AOC=90°,∵=2,∴∠COE=2∠AOE,∴∠COE=60°,而OE=OC,∴△OCE为等边三角形.∵DE//AB,OC⊥AB,∴DE⊥OC,
∴CD=OD.
(2)解:∵⊙O的直径是4,∴OE=OC=CF=2,CD=OD=1.在Rt△ODE中,DE ==.
在Rt △EFD中,EF = ==2.
16.解:如图,连接OC,交AB于点F,延长CD,交OA于点E.∵C是的中点,∴=,∴∠AOC=∠BOC=∠A0B=×120°=60°.∵0B=0A,∴∠OBF=∠OAF=30°,
∴∠BFO=90°,∴OC⊥AB.在Rt△BOF中,0B=QA=6∴0F=OB=3,∴CF=6-3=3.
∵CD⊥OA,∴∠OEC=90°,∴∠OCE=30°.∵∠CFD=90°,∴DF=,∴CD=2DF=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
2 圆的对称性
第2课时 圆心角的度数与它所对弧的度数的关系
基础闯关
知识点:弧的度数
1.若圆的一条弦把圆分成度数比为1:3的两条弧,则该弦所对的圆心角的度数是( )
A.90° B.45° C.135° D.45°或135°
2.如图,AB是⊙O的直径,四边形ABCD的各顶点均在⊙O上.若BC=CD=DA=2 cm,则⊙O的周长为( )
A.4πcm B.6πcm C.8πcm D.10πcm
3.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为____________.
4.如图,在⊙O中,直径AB∥弦CD.若∠COD=110°,则的度数为___________.
5.如图,⊙O经过五边形OABCD的四个顶点.若∠AOD=150°,∠A=65°,∠D=60°,则的度数为_____________.
6.如图,点C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO.若劣弧AD的度数为40°,则劣弧DE的度数为____________.
第6题图 第7题图
能力提升
7.如图,△ABC的两顶点A,B在⊙O上,点C在圆外,∠C=46°,边AC交⊙O于点D,DE∥BC且经过圆心交⊙O于点E,则的度数为( )
A.46° B.92° C.88° D.44°
8.如图,将大小不同的两个量角器的0°刻度线对齐,且小量角器的中心O2恰好在大量角器的圆周上,设图中两圆周的交点为P,且点P在小量角器上对应的刻度为63°,那么点P在大量角器上对应的刻度为(只考虑小于90°的角)( )
A.45° B.55° C.56° D.57°
9.如图,将△AOB绕点A顺时针旋转得到△ACD,使得点C,D都在⊙O上,且点C在BO的延长线上,则旋转角的度数为____________.
10.如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为___________.
素养提升
【模型意识——平行线与直径所夹的弧】
11.如图,已知AB是⊙O的直径,弦AC//OD.求证:=.
12.(变式1)如图,已知AB和CD是⊙O的两条直径,CE//AB.若的度数为40°,则的度数为_____________.
第12题图 第13题图
13.(变式2)如图,AB为半圆O的直径,C,D两点在上,且AD//OC,连接BC,BD.若=62°,则的度数为______________.
14.(变式3)如图,AB是⊙O的直径,E是⊙O上的一点,的度数为40°,过点O作OC//BE交⊙O于点C,则∠BOC的度数为_____________.
15.如图,AB是⊙O的直径,点C,E都在⊙O上,OC⊥AB,=2,DE//AB交OC于点D,延长OC至点F,使FC=OC,连接EF.
(1)求证:CD=OD.
(2)若⊙O的直径是4,求EF的长.
培优创新
16.[推理能力]如图,在扇形OAB中,∠AOB=120°,半径OA=6,C是弧AB的中点,CD⊥OA,交AB于点D,求CD的长.
参考答案
1.A 2.A 3.50° 4.35° 5.40°
6.120°[解析]∵劣弧AD的度数为40°,∴∠AOD=40°,CD=CO,∴ZD=ZCOD=40°,∴ZECO=2∠D=80°.∵OE=OD,∴ZE=ZD=40°,∴∠BOE=∠E+∠ECO=40°+80°=120°,∴劣弧BE的度数为120°。
7.C
8.A[解析]如图,连接O P,O P.∵P在小量角器上对应的刻度为63°,即ZO O P=63°,而O P=O O ,∴∠O PO =∠O O P=63°,∴∠PO O =180°-63°-63°=54°,即点P在大量角器上对应的刻度为54°.
9.60°
10.50°[解析]如图,连接OD.由题可知BC垂直平分OD,∴BD=B0.
∵OB=OD∴BD=BO=DO,∴△OBD为等边三角形,∴∠DOB=60°,∴/AOD=∠AOB-∠DOB=110°-60°=50°,∴的度数为50°。
11.证明:连接OC.∵OA=OC,∴∠OAC=∠ACO. ∵AC//OD,∴∠OAC=∠BOD,∠DOC=∠ACO,
∴∠BOD=∠COD,∴BD=CD.
12.70° 13.56°
14.110° [解析]连接OE.∵的度数为40°,∴∠BOE=40°.
∵OB=OE ,∴∠OBF=∠OEB=(180°-40)÷2=70°.∵OC//BE,∴∠BCO=∠CBE.
∵CO=BO,∴∠OBC=∠C ,∴∠CRF =∠OCB =∠OBC=∠OBE=35°,
∴∠BOC=180°-∠OBC-∠OCB=110°.
15.(1)证明:如图,连接OE,CE.∵OC⊥AB,∴∠AOC=90°,∵=2,∴∠COE=2∠AOE,∴∠COE=60°,而OE=OC,∴△OCE为等边三角形.∵DE//AB,OC⊥AB,∴DE⊥OC,
∴CD=OD.
(2)解:∵⊙O的直径是4,∴OE=OC=CF=2,CD=OD=1.在Rt△ODE中,DE ==.
在Rt △EFD中,EF = ==2.
16.解:如图,连接OC,交AB于点F,延长CD,交OA于点E.∵C是的中点,∴=,∴∠AOC=∠BOC=∠A0B=×120°=60°.∵0B=0A,∴∠OBF=∠OAF=30°,
∴∠BFO=90°,∴OC⊥AB.在Rt△BOF中,0B=QA=6∴0F=OB=3,∴CF=6-3=3.
∵CD⊥OA,∴∠OEC=90°,∴∠OCE=30°.∵∠CFD=90°,∴DF=,∴CD=2DF=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
