2023-2024学年山东省青岛市李沧区八年级(上)期中数学试卷(PDF版,含解析)
文档属性
| 名称 | 2023-2024学年山东省青岛市李沧区八年级(上)期中数学试卷(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 732.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 20:13:36 | ||
图片预览



文档简介
2023-2024 学年山东省青岛市李沧区八年级(上)期中数学试卷
一、选择题(本大题共 8 小题,每小题 3 分,共 24 分)
1.(3分) 的倒数是( )
A.﹣ B. C.﹣ D.
2.(3分)如图是由边长为 1m的方砖铺设的地板示意图,如果小球在地板上从点 A滚动到
点 B,则小球滚动的最短路程是( )
A.2m B.4m C. D.5m
3.(3 分)在平面直角坐标系内有一点 P(x,y),若点 P位于第二象限,并且点 P到 x轴
和 y轴的距离分别为 5,2,则点 P的坐标是( )
A.(5,2) B.(2,5) C.(2,﹣5) D.(﹣2,5)
4.(3分)若一次函数 y=2x﹣b的图象经过点(0,﹣3),则下列各点在该一次函数图象上
的是( )
A.(2,1) B.(2,3) C.(﹣1,1) D.(1,5)
5.(3分)下列说法正确的是( )
A.0.2是 0.4的算术平方根
B.﹣5是 25的平方根
C. 的算术平方根是 9
D.16的平方根是 4
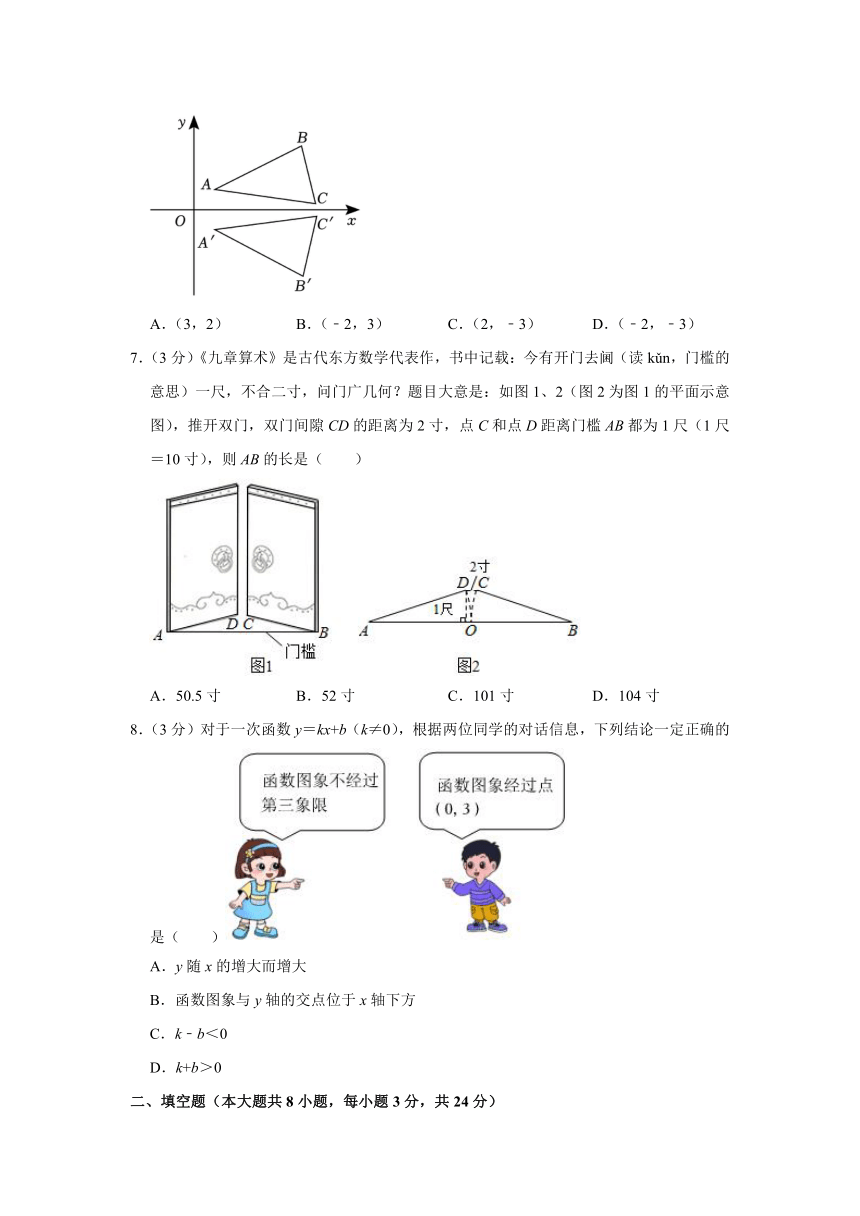
6.(3分)如图,在平面直角坐标系中,△ABC与△A'B'C'关于 x轴对称,其中点 A,B,C
的对应点分别为点 A',B',C',若点 P(2,3)在△ABC的边上,则点 P在△A'B'C'上的
对应点 P'的坐标是( )
A.(3,2) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
7.(3分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 kǔn,门槛的
意思)一尺,不合二寸,问门广几何?题目大意是:如图 1、2(图 2为图 1的平面示意
图),推开双门,双门间隙 CD的距离为 2寸,点 C和点 D距离门槛 AB都为 1尺(1尺
=10寸),则 AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
8.(3分)对于一次函数 y=kx+b(k≠0),根据两位同学的对话信息,下列结论一定正确的
是( )
A.y随 x的增大而增大
B.函数图象与 y轴的交点位于 x轴下方
C.k﹣b<0
D.k+b>0
二、填空题(本大题共 8 小题,每小题 3 分,共 24 分)
9.(3分) 的相反数是 .
10.(3分)已知一次函数 y=kx+3(k≠0),其函数值 y随 x值的增大而增大.当 x=﹣2时,
函数值 y可以是 (请写出一个你认为正确的即可).
11.(3分)如图,正方形的面积为 12,则与该正方形的边长最接近的整数是 .
12.(3 分)已知一次函数 y=ax﹣5 的图象经过点 A(﹣4,3),则关于 x的一元一次方程
ax﹣5=3的解为 .
13.(3分)如图,在四边形 ABCD中,∠ABC=∠CDA=90°,分别以四边形 ABCD的四
条边为边长,向外作四个正方形,面积分别为 S1,S2,S3,S4.若 S1=6,S2=10,S3=
12,则 S4的值为 .
14.(3 分)在同一直角坐标系中,直线 y1=3x+1 与 x轴,y轴分别交于 A,B两点,直线
y2=kx+b与 x轴,y轴分别交于 C,D两点.若 AB∥CD,点 D在点 B的下方,并且 BD
=6,则直线 y2的表达式为 .
15.(3分)如图,在直角坐标系中,长方形 OABC的顶点 A,C分别在 x轴,y轴上,点 A,
C的坐标分别为(﹣7,0),(0,4).E为边 BC上一点,点 D的坐标为(﹣5,0),若
△ODE是腰长为 5的等腰三角形,则点 E的坐标是 .
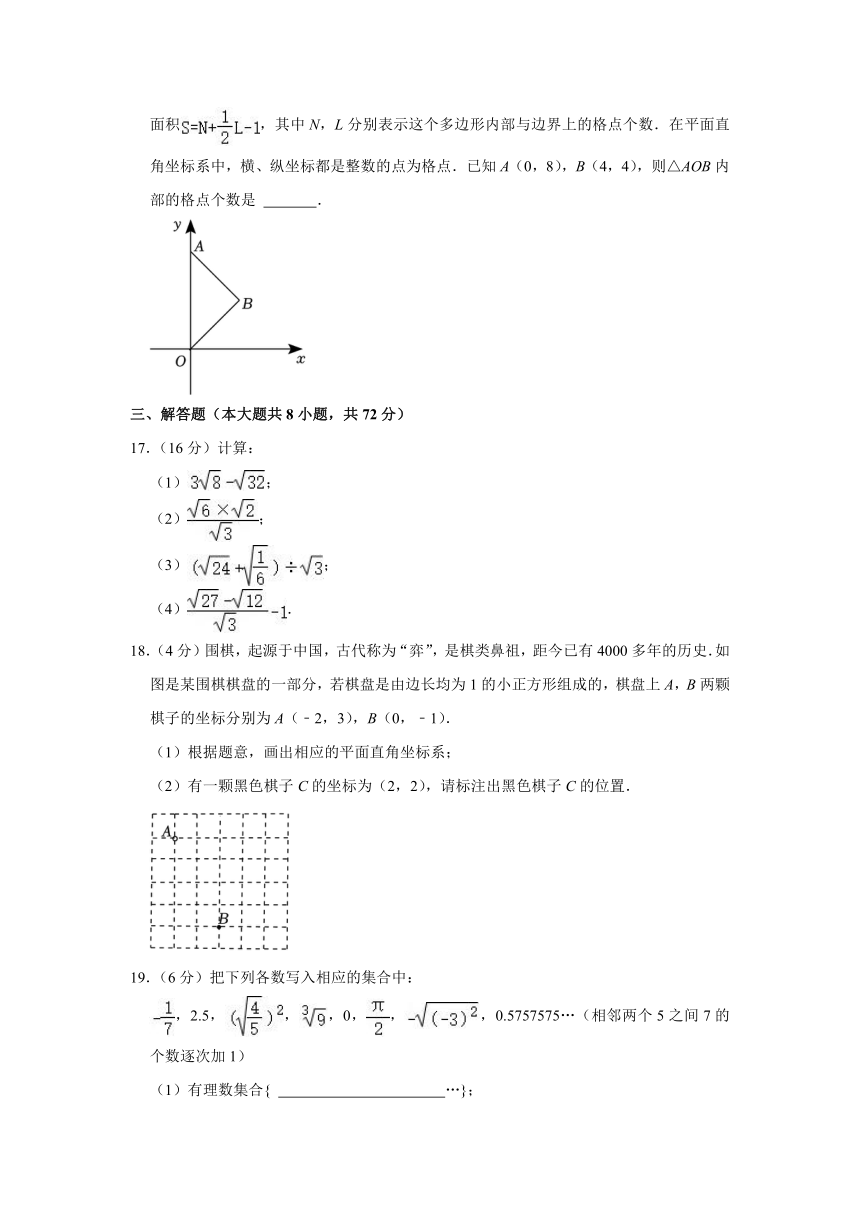
16.(3 分)皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的
面积 ,其中 N,L分别表示这个多边形内部与边界上的格点个数.在平面直
角坐标系中,横、纵坐标都是整数的点为格点.已知 A(0,8),B(4,4),则△AOB内
部的格点个数是 .
三、解答题(本大题共 8 小题,共 72 分)
17.(16分)计算:
(1) ;
(2) ;
(3) ;
(4) .
18.(4分)围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有 4000多年的历史.如
图是某围棋棋盘的一部分,若棋盘是由边长均为 1的小正方形组成的,棋盘上 A,B两颗
棋子的坐标分别为 A(﹣2,3),B(0,﹣1).
(1)根据题意,画出相应的平面直角坐标系;
(2)有一颗黑色棋子 C的坐标为(2,2),请标注出黑色棋子 C的位置.
19.(6分)把下列各数写入相应的集合中:
,2.5, , ,0, , ,0.5757575…(相邻两个 5 之间 7 的
个数逐次加 1)
(1)有理数集合{ …};
(2)无理数集合{ …}.
20.(8 分)党的十八大以来,各地积极推动城市绿化工作,大力拓展城市生态空间,让许
多城市再现绿水青山、某小区物业在小区拐角清理出了一块空地进行绿化改造,如图,
∠ABC=90°,AB=12m,BC=9m,AD=17m,CD=8m.
(1)为了方便居民的生活,在绿化时将修一条从点 A直通点 C的小路,求小路 AC的长
度;
(2)若该空地的改造费用为每平方米 150元,试计算改造这片空地共需花费多少元?
21.(8分)我们知道 是无理数,因此 的小数部分我们不可能全部写出来,于是小明
用 来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是
有道理的,因为 的整数部分是 1,将这个数减去其整数部分,差就是小数部分.又例
如: ,即 ,所以 的整数部分为 2,小数部分为 .请
根据以上信息,回答下列问题:
(1) 整数部分是 ,小数部分是 ;
(2)如果 的整数部分为 a, 的整数部分为 b,求 12a+7b的立方根;
(3)已知 ,其中 x是整数,且 0<y<1,求 x+y的值.
22.(8分)在平面直角坐标系中,A,B两点的坐标分别是 A(0,a),B(0,b),且 +|12
﹣b|=0.
(1)求 b﹣a的平方根;
(2)若在 x轴的正半轴上有一点 C,且△ABC的面积是 27,求点 C的坐标;
(3)过(2)中的点 C作直线 MN∥y轴,在直线 MN上是否存在点 D,使得△ACD的
面积是△ABC面积的 ?若存在,请求出点 D的坐标;若不存在,请说明理由.
23.(10 分)如图,一次函数 y1=ax+b的图象与 y轴负半轴相交于点 A,与正比例函数 y2
=kx的图象交于点 B(﹣8,6),且 .
(1)求正比例函数与一次函数的表达式;
(2)请直接写出当 y1>y2时,x的取值范围.
24.(12分)通过小学的学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之
间会产生阻碍物体运动的力、像这样的力是摩擦力.小明利用如图 1所示的装置测量在
不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的
木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到
的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成如表:
砝码的质量 0 50 100 150 200 250
m/g
滑动摩擦力 f/N 1.8 2.0 2.2 2.4 2.6 2.8
(1)请在图 2的平面直角坐标系内,描出六次测量的有序数对(m,f)所对应的六个点;
(2)这些点是否在一条直线上?如果是,请确定 f与 m的关系式;如果不是,请说明理
由;
(3)在某次实验中,测得木块受到的摩擦力为 4.2N,则此时砝码的质量是多少?
(4)在实验过程中,当砝码的质量为 100g~800g时,请直接写出木块受到的摩擦力的
最大值和最小值分别为多少?
2023-2024 学年山东省青岛市李沧区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共 8 小题,每小题 3 分,共 24 分)
1.(3分) 的倒数是( )
A.﹣ B. C.﹣ D.
【分析】根据倒数的定义求解即可.
【解答】解: 的倒数是 ,
故选:D.
【点评】本题考查了实数的性质,分子分母交换位置是求一个数的倒数的关键.
2.(3分)如图是由边长为 1m的方砖铺设的地板示意图,如果小球在地板上从点 A滚动到
点 B,则小球滚动的最短路程是( )
A.2m B.4m C. D.5m
【分析】根据勾股定理结合网格求出 AB的长即可.
【解答】解:由题意得,小球滚动的最短路程为 AB= =2 (m),
故选:C.
【点评】本题考查了勾股定理,熟记勾股定理是解题的关键.
3.(3 分)在平面直角坐标系内有一点 P(x,y),若点 P位于第二象限,并且点 P到 x轴
和 y轴的距离分别为 5,2,则点 P的坐标是( )
A.(5,2) B.(2,5) C.(2,﹣5) D.(﹣2,5)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数以及点到 x轴的距离等于纵
坐标的绝对值,到 y轴的距离等于横坐标的绝对值解答.
【解答】解:∵点 P在第二象限内,
∴点 P的横坐标为负数,纵坐标为正数,
∵点 P到 x轴的距离为 5,到 y轴的距离为 2,
∴点 P的坐标为(﹣2,5),故 D正确.
故选:D.
【点评】本题主要考查了点到坐标轴的距离,熟练掌握点到 x轴的距离等于纵坐标的绝
对值,到 y轴的距离等于横坐标的绝对值是解题的关键.
4.(3分)若一次函数 y=2x﹣b的图象经过点(0,﹣3),则下列各点在该一次函数图象上
的是( )
A.(2,1) B.(2,3) C.(﹣1,1) D.(1,5)
【分析】由一次函数 y=2x﹣b的图象经过点(0,﹣3),利用一次函数图象上点的坐标
特征,可求出 b值,进而可得出一次函数解析式,逐一代入各选项中点的横坐标,求出 y
值,再与点的纵坐标比较后,即可得出结论.
【解答】解:∵一次函数 y=2x﹣b的图象经过点(0,﹣3),
∴﹣3=2×0﹣b,
解得:b=3,
∴一次函数解析式为 y=2x﹣3.
A.当 x=2时,y=2×2﹣3=1,
∴点(2,1)在该一次函数图象上,选项 A符合题意;
B.当 x=2时,y=2×2﹣3=1,1≠3,
∴点(2,3)不在该一次函数图象上,选项 B不符合题意;
C.当 x=﹣1时,y=2×(﹣1)﹣3=﹣5,﹣5≠1,
∴点(﹣1,1)不在该一次函数图象上,选项 C不符合题意;
D.当 x=1时,y=2×1﹣3=﹣1,﹣1≠5,
∴点(1,5)不在该一次函数图象上,选项 D不符合题意.
故选:A.
【点评】本题考查了一次函数图象上点的坐标特征,利用一次函数图象上点的坐标特征,
求出 b值是解题的关键.
5.(3分)下列说法正确的是( )
A.0.2是 0.4的算术平方根
B.﹣5是 25的平方根
C. 的算术平方根是 9
D.16的平方根是 4
【分析】根据算术平方根及平方根的定义逐项判断即可.
【解答】解:0.2是 0.04的算术平方根,则 A不符合题意;
﹣5是 25的平方根,则 B符合题意;
=9,其算术平方根是 3,则 C不符合题意;
16的平方根是±4,则 D不符合题意;
故选:B.
【点评】本题考查平方根及算术平方根,熟练掌握相关定义是解题的关键.
6.(3分)如图,在平面直角坐标系中,△ABC与△A'B'C'关于 x轴对称,其中点 A,B,C
的对应点分别为点 A',B',C',若点 P(2,3)在△ABC的边上,则点 P在△A'B'C'上的
对应点 P'的坐标是( )
A.(3,2) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
【分析】利用关于 x轴的对称点的坐标特点可得答案.
【解答】解:∵△ABC与△A'B'C'关于 x轴对称,点 P(2,3)在△ABC的边上,
∴点 P在△A'B'C'上的对应点 P'的坐标是(2,﹣3).
故选:C.
【点评】此题主要考查了关于 x轴的对称点的坐标,关键是掌握关于 x轴的对称点的坐
标特点:横坐标不变,纵坐标互为相反数.
7.(3分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 kǔn,门槛的
意思)一尺,不合二寸,问门广几何?题目大意是:如图 1、2(图 2为图 1的平面示意
图),推开双门,双门间隙 CD的距离为 2寸,点 C和点 D距离门槛 AB都为 1尺(1尺
=10寸),则 AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
【分析】取 AB的中点 O,过 D作 DE⊥AB于 E,根据勾股定理解答即可得到结论.
【解答】解:取 AB的中点 O,过 D作 DE⊥AB于 E,如图 2所示:
由题意得:OA=OB=AD=BC,
设 OA=OB=AD=BC=r寸,
则 AB=2r(寸),DE=10(寸),OE= CD=1(寸),AE=(r﹣1)寸,
在 Rt△ADE中,AE2+DE2=AD2,
即(r﹣1)2+102=r2,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸,
故选:C.
【点评】本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.
8.(3分)对于一次函数 y=kx+b(k≠0),根据两位同学的对话信息,下列结论一定正确的
是( )
A.y随 x的增大而增大
B.函数图象与 y轴的交点位于 x轴下方
C.k﹣b<0
D.k+b>0
【分析】根据一次函数的性质以及一次函数图象上点的坐标特征判断即可.
【解答】解:∵一次函数 y=kx+b(k≠0)的图象不经过第三象限,
∴一次函数 y=kx+b(k≠0)的图象经过经过第二、四象限或第一、二、四象限,
∴k<0,
∴y随 x的增大而减小,故 A错误,不合题意;
又∵函数图象经过点(0,3),
∴函数图象与 y轴的交点位于 x轴上方,故 B错误,不合题意;
∵k<0,b=3>0,
∴k﹣b<0,故选项 C正确,符合题意;
k+b不一定大于 0,故选项 D错误,不合题意.
故选:C.
【点评】本题考查一次函数的图象及性质;熟练掌握一次函数解析式 y=kx+b中,k与 b
对函数图象的影响是解题的关键.
二、填空题(本大题共 8 小题,每小题 3 分,共 24 分)
9.(3分) 的相反数是 4 .
【分析】先求出 的值,再求出相反数即可.
【解答】解:由立方根的计算方法可知 =﹣4,
因为﹣4的相反数为 4,
所以 的相反数为 4.
故答案为:4.
【点评】本题主要考查了相反数和立方根的有关知识.
10.(3分)已知一次函数 y=kx+3(k≠0),其函数值 y随 x值的增大而增大.当 x=﹣2时,
函数值 y可以是 1(答案不唯一) (请写出一个你认为正确的即可).
【分析】由函数值 y随 x值的增大而增大,可得出 k>0,取 k=1,再代入 x=﹣2,求出
y值即可.
【解答】解:∵一次函数 y=kx+3(k≠0),其函数值 y随 x值的增大而增大,
∴k>0,
取 k=1,则一次函数解析式为 y=x+3.
当 x=﹣2时,y=﹣2+3=1.
故答案为:1(答案不唯一).
【点评】本题考查了一次函数图象上点的坐标特征以及一次函数的性质,利用一次函数
的性质,找出 k的取值范围是解题的关键.
11.(3分)如图,正方形的面积为 12,则与该正方形的边长最接近的整数是 3 .
【分析】由于正方形的面积为 12,利用算术平方根的定义可得到正方形的边长为 ,
根据 9<12<16可得到与 最接近的整数为 3.
【解答】解:∵正方形的面积为 12,
∴正方形的边长为 ,
∵9<12<16,
∴3< <4,
∵9<12<12.25,
∴3< <3.5,
∴ 最接近的整数为 3.
故答案为:3.
【点评】本题考查了估算无理数的大小,算术平方根.能够正确估算无理数的大小:利
用完全平方数和算术平方根对无理数的大小进行估算是解题的关键.
12.(3 分)已知一次函数 y=ax﹣5 的图象经过点 A(﹣4,3),则关于 x的一元一次方程
ax﹣5=3的解为 x=﹣4 .
【分析】由一次函数 y=ax﹣5的图象经过点 A(﹣4,3)可知,x=﹣4时,函数 y=3,
即 ax﹣5=3,从而得到关于 x的一元一次方程 ax﹣5=3的解为 x=﹣4.
【解答】解:∵一次函数 y=ax﹣5的图象经过点 A(﹣4,3),
∴于 x的一元一次方程 ax﹣5=3的解为 x=﹣4.
故答案为:x=﹣4.
【点评】本题考查了一次函数与一元一次方程,属于基础题,关键是掌握用数形结合的
方法解题.
13.(3分)如图,在四边形 ABCD中,∠ABC=∠CDA=90°,分别以四边形 ABCD的四
条边为边长,向外作四个正方形,面积分别为 S1,S2,S3,S4.若 S1=6,S2=10,S3=
12,则 S4的值为 16 .
【分析】连接 AC,根据 S4=S2+S3﹣S1即可得出结果.
【解答】解:如图,连接 AC,
∵S1=6,S2=10,S3=12,
∴AD2=6,AB2=10,BC2=12,
在 Rt△ABC与 Rt△ADC中,由勾股定理得,
AC2=AB2+BC2=22,
CD2=AC2﹣AD2,
∴CD2=22﹣6=16,
∴S4=16,
故答案为:16.
【点评】本题考查了勾股定理,正确得出 S4=S2+S3﹣S1是解题的关键.
14.(3 分)在同一直角坐标系中,直线 y1=3x+1 与 x轴,y轴分别交于 A,B两点,直线
y2=kx+b与 x轴,y轴分别交于 C,D两点.若 AB∥CD,点 D在点 B的下方,并且 BD
=6,则直线 y2的表达式为 y2=3x﹣5 .
【分析】由题意可知,将直线 y1=3x+1向下平移 6个单位得到直线 y2.
【解答】解:由题意可知将直线 y1=3x+1向下平移 6个单位得到直线 y2,
故直线 y2的表达式为 y2=3x+1﹣6=3x﹣5.
故答案为:y2=3x﹣5.
【点评】本题考查的是一次函数图象上点的坐标特征,能够明确题意,利用“上加下减”
的平移原则是解答此题的关键.
15.(3分)如图,在直角坐标系中,长方形 OABC的顶点 A,C分别在 x轴,y轴上,点 A,
C的坐标分别为(﹣7,0),(0,4).E为边 BC上一点,点 D的坐标为(﹣5,0),若
△ODE是腰长为 5的等腰三角形,则点 E的坐标是 (﹣2,4)或(﹣3,4) .
【分析】分两种情况讨论,一是 DE=OD=5,作 DF⊥x轴交 BC于点 F,则 F(﹣5,4),
∠DFE=90°,由勾股定理得 EF= =3,则 CE=CF﹣EF=2,所以 E(﹣2,
4);二是 OE=OD=5,则 CE= =3,所以 E(﹣3,4),于是得到问题的答
案.
【解答】解:∵四边形 OABC是矩形,A(﹣7,0),C(0,4),
∴OC=4,BC=OA=7,BC∥x轴,∠OCB=90°,
∵E为边 BC上一点,
∴点 E的纵坐标为 4,
∵D(﹣5,0),△ODE是腰长为 5的等腰三角形,
∴DE=OD=5或 OE=OD=5,
如图 1,DE=OD=5,
作 DF⊥x轴交 BC于点 F,则 F(﹣5,4),∠DFE=90°,
∴CF=5,DF=4,
∴EF= = =3,
∴CE=CF﹣EF=5﹣3=2,
∴E(﹣2,4);
如图 2,OE=OD=5,则 CE= = =3,
∴E(﹣3,4),
综上所述,点 E的坐标是(﹣2,4)或(﹣3,4),
故答案为:(﹣2,4)或(﹣3,4).
【点评】此题重点考查图形与坐标、矩形的性质、等腰三角形的判定、勾股定理、数形
结合与分类讨论数学思想的运用等知识与方法,正确地作出辅助线构造直角三角形是解
题的关键.
16.(3 分)皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的
面积 ,其中 N,L分别表示这个多边形内部与边界上的格点个数.在平面直
角坐标系中,横、纵坐标都是整数的点为格点.已知 A(0,8),B(4,4),则△AOB内
部的格点个数是 9 .
【分析】根据皮克定理及三角形边界上的格点的个数,可列出关于 N,L的二元一次方程
组,解之即可得出结论.
【解答】解:∵点 A的坐标为(0,8),点 B的坐标为(4,4),
∴△AOB的面积为 ×8×4=16,
即 N+ L﹣1=16①;
∵边 OA上的格点数是 9,边 OB上的格点数是 5,边 AB上的格点数是 5,
∴L=9+5+5﹣3②.
联立①②组成方程组得: ,
解得: ,
∴△AOB内部的格点个数是 9.
故答案为:9.
【点评】本题考查了二元一次方程组的应用以及坐标与图形性质,找准等量关系,正确
列出二元一次方程组是解题的关键.
三、解答题(本大题共 8 小题,共 72 分)
17.(16分)计算:
(1) ;
(2) ;
(3) ;
(4) .
【分析】(1)根据二次根式的性质化简,再合并同类二次根式即可;
(2)先计算乘法,再计算除法即可;
(3)先计算二次根式的除法,再计算加法即可;
(4)先计算二次根式的除法,再计算减法即可.
【解答】解:(1)
=6 ﹣4
=2 ;
(2)
=
=
=2;
(3)
= +
=2 +
= ;
(4)
= ﹣ ﹣1
=3﹣2﹣1
=0.
【点评】本题考查二次根式的混合运算,熟练掌握相关运算法则是解题的关键.
18.(4分)围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有 4000多年的历史.如
图是某围棋棋盘的一部分,若棋盘是由边长均为 1的小正方形组成的,棋盘上 A,B两颗
棋子的坐标分别为 A(﹣2,3),B(0,﹣1).
(1)根据题意,画出相应的平面直角坐标系;
(2)有一颗黑色棋子 C的坐标为(2,2),请标注出黑色棋子 C的位置.
【分析】(1)利用 A、B点坐标画出对应的直角坐标系;
(2)根据点的坐标作出点 C的位置即可.
【解答】解:(1)建立如图所示的直角坐标系;
(2)如图,点 C即为所求.
【点评】本题考查坐标确定位置,解题关键是正确作出图形,属于中考常考题型.
19.(6分)把下列各数写入相应的集合中:
,2.5, , ,0, , ,0.5757575…(相邻两个 5 之间 7 的
个数逐次加 1)
(1)有理数集合{ ﹣ ,2.5,( )2,0,﹣ …};
(2)无理数集合{ , ,0.5757575…(相邻两个 5之间 7的个数逐次加 1) …}.
【分析】根据实数的分类及二次根式的性质解答即可.
【解答】解:( )2= ,,﹣ =﹣3,
(1)有理数集合{﹣ ,2.5,( )2,0,﹣ ,...}.
故答案为:﹣ ,2.5,( )2,0,﹣ ;
(2)无理数集合{ , ,0.5757575…(相邻两个 5之间 7的个数逐次加 1),..}
故答案为: , ,0.5757575…(相邻两个 5之间 7的个数逐次加 1).
【点评】本题考查的是实数的分类及二次根式的性质与化简,熟知实数的分类是解题的
关键.
20.(8 分)党的十八大以来,各地积极推动城市绿化工作,大力拓展城市生态空间,让许
多城市再现绿水青山、某小区物业在小区拐角清理出了一块空地进行绿化改造,如图,
∠ABC=90°,AB=12m,BC=9m,AD=17m,CD=8m.
(1)为了方便居民的生活,在绿化时将修一条从点 A直通点 C的小路,求小路 AC的长
度;
(2)若该空地的改造费用为每平方米 150元,试计算改造这片空地共需花费多少元?
【分析】(1)根据勾股定理求出 AC即可;
(2)由勾股定理的逆定理得出三角形 ACD是直角三角,再根据三角形的面积公式求解
即可.
【解答】解:(1)在 Rt△ABC中,由勾股定理得,
AC= = =15(m),
答:小路 AC的长度为 15m;
(2)∵AC2+CD2=152+82=172=AD2,
∴△ACD是直角三角形,
∴S 2四边形 ABCD= = =114(m ),
114×150=17100(元).
答:改造这片空地共需花费 17100元.
【点评】本题考查了勾股定理的应用,熟记勾股定理是解题的关键.
21.(8分)我们知道 是无理数,因此 的小数部分我们不可能全部写出来,于是小明
用 来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是
有道理的,因为 的整数部分是 1,将这个数减去其整数部分,差就是小数部分.又例
如: ,即 ,所以 的整数部分为 2,小数部分为 .请
根据以上信息,回答下列问题:
(1) 整数部分是 5 ,小数部分是 ﹣5 ;
(2)如果 的整数部分为 a, 的整数部分为 b,求 12a+7b的立方根;
(3)已知 ,其中 x是整数,且 0<y<1,求 x+y的值.
【分析】(1)估算出 在哪两个连续整数之间即可;
(2)分别估算出 及 在哪两个连续整数之间后即可求得 a,b的值,然后将其代
入 12a+7b中计算,最后根据立方根的定义即可求得答案;
(3)估算出 9﹣ 的范围后即可确定 x,y的值,然后将其代入 x+y中计算即可.
【解答】解:(1)∵5< <6,
∴ 的整数部分是 5,小数部分是 ﹣5.
故答案为:5, ﹣5;
(2)∵ 的整数部分为 a,且 3< <4,
∴a=3,
∵ 的整数部分为 b,4< <5,
∴b=4,
∴12a+7b=12×3+7×4=64,
∴12a+7b的立方根是 4.
(3)∵2< <3,
∴6<9﹣ <7,
∵ ,其中 x是整数,且 0<y<1,
∴x=7,y= ﹣2,
∴x+y=7+( ﹣2)=5+ .
则 x+y的值为 5+ .
【点评】本题考查的是无理数的计算,估算无理数的整数部分是解题关键.
22.(8分)在平面直角坐标系中,A,B两点的坐标分别是 A(0,a),B(0,b),且 +|12
﹣b|=0.
(1)求 b﹣a的平方根;
(2)若在 x轴的正半轴上有一点 C,且△ABC的面积是 27,求点 C的坐标;
(3)过(2)中的点 C作直线 MN∥y轴,在直线 MN上是否存在点 D,使得△ACD的
面积是△ABC面积的 ?若存在,请求出点 D的坐标;若不存在,请说明理由.
【分析】(1)根据平方根和绝对值具有非负性即可求出 a,b的值;
(2)假设有一点 C,使得△ABC的面积是 27,AB=18,即可求出三角形的高,从而求
出点 C的坐标;
(3)由(2)知△ABC的面积是 27,则△ACD的面积是 3,由 MN∥y轴得出△ACD的
高是 3,求出底即可求出 C的坐标.
【解答】解:(1)∵ +|12﹣b|=0.
∴a+6=0,12﹣b=0,
∴a=﹣6,b=12,
∴b﹣a=12﹣(﹣6)=18,
∴b﹣a的平方根为±3 ;
(2)由(1)知 A(0,﹣6),B(0,12),
∴AB=18,
∴S△ABC= AB OC= ×18 OC=27,
解得 OC=3,
∵C在 x轴的正半轴上,
∴C的坐标为(3,0);
(3)存在,由(2)知△ABC的面积是 27,
∴△ACD的面积是 3,
∵MN∥y轴,
∴△ACD的高是 3,
∴S△ACD= CD 3=3,
解得 CD=2,
∵C在直线 MN上,
∴C的坐标为(3,2)或(3,﹣2).
【点评】本题考查三角形的面积,平面直角坐标系,平方根和绝对值的性质,熟练掌握
以上知识是解题关键.
23.(10 分)如图,一次函数 y1=ax+b的图象与 y轴负半轴相交于点 A,与正比例函数 y2
=kx的图象交于点 B(﹣8,6),且 .
(1)求正比例函数与一次函数的表达式;
(2)请直接写出当 y1>y2时,x的取值范围.
【分析】(1)利用待定系数法求解即可;
(2)观察图象即可求解.
【解答】解:(1)∵正比例函数 y2=kx的图象过点 B(﹣8,6),
∴6=﹣8k,
∴k=﹣ ,
∴正比例函数的表达式为 y2=﹣ x;
由 B(﹣8,6)可知 OB= =10,
∵ ,
∴OA=5,
∴A(0,﹣5),
把 A、B的坐标代入 y1=ax+b得 ,
解得 ,
∴一次函数的表达式为 y1=﹣ x﹣5;
(2)由图象可知,当 y1>y2时,x的取值范围是 x<﹣8.
【点评】本题考查了一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及
一次函数与不等式,数形结合是解题的关键.
24.(12分)通过小学的学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之
间会产生阻碍物体运动的力、像这样的力是摩擦力.小明利用如图 1所示的装置测量在
不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的
木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到
的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成如表:
砝码的质量 0 50 100 150 200 250
m/g
滑动摩擦力 f/N 1.8 2.0 2.2 2.4 2.6 2.8
(1)请在图 2的平面直角坐标系内,描出六次测量的有序数对(m,f)所对应的六个点;
(2)这些点是否在一条直线上?如果是,请确定 f与 m的关系式;如果不是,请说明理
由;
(3)在某次实验中,测得木块受到的摩擦力为 4.2N,则此时砝码的质量是多少?
(4)在实验过程中,当砝码的质量为 100g~800g时,请直接写出木块受到的摩擦力的
最大值和最小值分别为多少?
【分析】(1)在平面直角坐标系中描点即可;
(2)将(1)中的 6个点连接起来,判断是否为直线.如果是直线,则利用待定系数法
求出 f与 m的关系式即可;
(3)当 f=4.2时,求出对应 m的值即可;
(4)由 f与 m的关系式,确定 f随 m的增减性,根据 m的取值范围,分别求出 f的最大
值和最小值即可.
【解答】解:(1)在平面直角坐标系中六次测量的有序数对(m,f)所对应的六个点如
图所示:
(2)如上图所示,这些点在一条直线上.
设 f与 m的关系式为 f=km+b,将(0,1.8)和(50,2.0)代入,
得 ,解得 ,
∴f与 m的关系式为 f=0.004m+1.8.
(3)当 f=4.2时,0.004m+1.8=4.2,解得 m=600,
∴此时砝码的质量是 600g.
(4)∵f随 m的增大而增大,
∴当 m=800时,f值最大,此时 f=0.004×800+1.8=5.0;
当 m=100时,f值最小,此时 f=0.004×100+1.8=2.2.
∴当砝码的质量为 100g~800g时,木块受到的摩擦力的最大值和最小值分别为 5.0N,
2.2N.
【点评】本题考查函数的表示方法等,利用待定系数法求出函数的解析式是解题的关键.
一、选择题(本大题共 8 小题,每小题 3 分,共 24 分)
1.(3分) 的倒数是( )
A.﹣ B. C.﹣ D.
2.(3分)如图是由边长为 1m的方砖铺设的地板示意图,如果小球在地板上从点 A滚动到
点 B,则小球滚动的最短路程是( )
A.2m B.4m C. D.5m
3.(3 分)在平面直角坐标系内有一点 P(x,y),若点 P位于第二象限,并且点 P到 x轴
和 y轴的距离分别为 5,2,则点 P的坐标是( )
A.(5,2) B.(2,5) C.(2,﹣5) D.(﹣2,5)
4.(3分)若一次函数 y=2x﹣b的图象经过点(0,﹣3),则下列各点在该一次函数图象上
的是( )
A.(2,1) B.(2,3) C.(﹣1,1) D.(1,5)
5.(3分)下列说法正确的是( )
A.0.2是 0.4的算术平方根
B.﹣5是 25的平方根
C. 的算术平方根是 9
D.16的平方根是 4
6.(3分)如图,在平面直角坐标系中,△ABC与△A'B'C'关于 x轴对称,其中点 A,B,C
的对应点分别为点 A',B',C',若点 P(2,3)在△ABC的边上,则点 P在△A'B'C'上的
对应点 P'的坐标是( )
A.(3,2) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
7.(3分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 kǔn,门槛的
意思)一尺,不合二寸,问门广几何?题目大意是:如图 1、2(图 2为图 1的平面示意
图),推开双门,双门间隙 CD的距离为 2寸,点 C和点 D距离门槛 AB都为 1尺(1尺
=10寸),则 AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
8.(3分)对于一次函数 y=kx+b(k≠0),根据两位同学的对话信息,下列结论一定正确的
是( )
A.y随 x的增大而增大
B.函数图象与 y轴的交点位于 x轴下方
C.k﹣b<0
D.k+b>0
二、填空题(本大题共 8 小题,每小题 3 分,共 24 分)
9.(3分) 的相反数是 .
10.(3分)已知一次函数 y=kx+3(k≠0),其函数值 y随 x值的增大而增大.当 x=﹣2时,
函数值 y可以是 (请写出一个你认为正确的即可).
11.(3分)如图,正方形的面积为 12,则与该正方形的边长最接近的整数是 .
12.(3 分)已知一次函数 y=ax﹣5 的图象经过点 A(﹣4,3),则关于 x的一元一次方程
ax﹣5=3的解为 .
13.(3分)如图,在四边形 ABCD中,∠ABC=∠CDA=90°,分别以四边形 ABCD的四
条边为边长,向外作四个正方形,面积分别为 S1,S2,S3,S4.若 S1=6,S2=10,S3=
12,则 S4的值为 .
14.(3 分)在同一直角坐标系中,直线 y1=3x+1 与 x轴,y轴分别交于 A,B两点,直线
y2=kx+b与 x轴,y轴分别交于 C,D两点.若 AB∥CD,点 D在点 B的下方,并且 BD
=6,则直线 y2的表达式为 .
15.(3分)如图,在直角坐标系中,长方形 OABC的顶点 A,C分别在 x轴,y轴上,点 A,
C的坐标分别为(﹣7,0),(0,4).E为边 BC上一点,点 D的坐标为(﹣5,0),若
△ODE是腰长为 5的等腰三角形,则点 E的坐标是 .
16.(3 分)皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的
面积 ,其中 N,L分别表示这个多边形内部与边界上的格点个数.在平面直
角坐标系中,横、纵坐标都是整数的点为格点.已知 A(0,8),B(4,4),则△AOB内
部的格点个数是 .
三、解答题(本大题共 8 小题,共 72 分)
17.(16分)计算:
(1) ;
(2) ;
(3) ;
(4) .
18.(4分)围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有 4000多年的历史.如
图是某围棋棋盘的一部分,若棋盘是由边长均为 1的小正方形组成的,棋盘上 A,B两颗
棋子的坐标分别为 A(﹣2,3),B(0,﹣1).
(1)根据题意,画出相应的平面直角坐标系;
(2)有一颗黑色棋子 C的坐标为(2,2),请标注出黑色棋子 C的位置.
19.(6分)把下列各数写入相应的集合中:
,2.5, , ,0, , ,0.5757575…(相邻两个 5 之间 7 的
个数逐次加 1)
(1)有理数集合{ …};
(2)无理数集合{ …}.
20.(8 分)党的十八大以来,各地积极推动城市绿化工作,大力拓展城市生态空间,让许
多城市再现绿水青山、某小区物业在小区拐角清理出了一块空地进行绿化改造,如图,
∠ABC=90°,AB=12m,BC=9m,AD=17m,CD=8m.
(1)为了方便居民的生活,在绿化时将修一条从点 A直通点 C的小路,求小路 AC的长
度;
(2)若该空地的改造费用为每平方米 150元,试计算改造这片空地共需花费多少元?
21.(8分)我们知道 是无理数,因此 的小数部分我们不可能全部写出来,于是小明
用 来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是
有道理的,因为 的整数部分是 1,将这个数减去其整数部分,差就是小数部分.又例
如: ,即 ,所以 的整数部分为 2,小数部分为 .请
根据以上信息,回答下列问题:
(1) 整数部分是 ,小数部分是 ;
(2)如果 的整数部分为 a, 的整数部分为 b,求 12a+7b的立方根;
(3)已知 ,其中 x是整数,且 0<y<1,求 x+y的值.
22.(8分)在平面直角坐标系中,A,B两点的坐标分别是 A(0,a),B(0,b),且 +|12
﹣b|=0.
(1)求 b﹣a的平方根;
(2)若在 x轴的正半轴上有一点 C,且△ABC的面积是 27,求点 C的坐标;
(3)过(2)中的点 C作直线 MN∥y轴,在直线 MN上是否存在点 D,使得△ACD的
面积是△ABC面积的 ?若存在,请求出点 D的坐标;若不存在,请说明理由.
23.(10 分)如图,一次函数 y1=ax+b的图象与 y轴负半轴相交于点 A,与正比例函数 y2
=kx的图象交于点 B(﹣8,6),且 .
(1)求正比例函数与一次函数的表达式;
(2)请直接写出当 y1>y2时,x的取值范围.
24.(12分)通过小学的学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之
间会产生阻碍物体运动的力、像这样的力是摩擦力.小明利用如图 1所示的装置测量在
不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的
木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到
的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成如表:
砝码的质量 0 50 100 150 200 250
m/g
滑动摩擦力 f/N 1.8 2.0 2.2 2.4 2.6 2.8
(1)请在图 2的平面直角坐标系内,描出六次测量的有序数对(m,f)所对应的六个点;
(2)这些点是否在一条直线上?如果是,请确定 f与 m的关系式;如果不是,请说明理
由;
(3)在某次实验中,测得木块受到的摩擦力为 4.2N,则此时砝码的质量是多少?
(4)在实验过程中,当砝码的质量为 100g~800g时,请直接写出木块受到的摩擦力的
最大值和最小值分别为多少?
2023-2024 学年山东省青岛市李沧区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共 8 小题,每小题 3 分,共 24 分)
1.(3分) 的倒数是( )
A.﹣ B. C.﹣ D.
【分析】根据倒数的定义求解即可.
【解答】解: 的倒数是 ,
故选:D.
【点评】本题考查了实数的性质,分子分母交换位置是求一个数的倒数的关键.
2.(3分)如图是由边长为 1m的方砖铺设的地板示意图,如果小球在地板上从点 A滚动到
点 B,则小球滚动的最短路程是( )
A.2m B.4m C. D.5m
【分析】根据勾股定理结合网格求出 AB的长即可.
【解答】解:由题意得,小球滚动的最短路程为 AB= =2 (m),
故选:C.
【点评】本题考查了勾股定理,熟记勾股定理是解题的关键.
3.(3 分)在平面直角坐标系内有一点 P(x,y),若点 P位于第二象限,并且点 P到 x轴
和 y轴的距离分别为 5,2,则点 P的坐标是( )
A.(5,2) B.(2,5) C.(2,﹣5) D.(﹣2,5)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数以及点到 x轴的距离等于纵
坐标的绝对值,到 y轴的距离等于横坐标的绝对值解答.
【解答】解:∵点 P在第二象限内,
∴点 P的横坐标为负数,纵坐标为正数,
∵点 P到 x轴的距离为 5,到 y轴的距离为 2,
∴点 P的坐标为(﹣2,5),故 D正确.
故选:D.
【点评】本题主要考查了点到坐标轴的距离,熟练掌握点到 x轴的距离等于纵坐标的绝
对值,到 y轴的距离等于横坐标的绝对值是解题的关键.
4.(3分)若一次函数 y=2x﹣b的图象经过点(0,﹣3),则下列各点在该一次函数图象上
的是( )
A.(2,1) B.(2,3) C.(﹣1,1) D.(1,5)
【分析】由一次函数 y=2x﹣b的图象经过点(0,﹣3),利用一次函数图象上点的坐标
特征,可求出 b值,进而可得出一次函数解析式,逐一代入各选项中点的横坐标,求出 y
值,再与点的纵坐标比较后,即可得出结论.
【解答】解:∵一次函数 y=2x﹣b的图象经过点(0,﹣3),
∴﹣3=2×0﹣b,
解得:b=3,
∴一次函数解析式为 y=2x﹣3.
A.当 x=2时,y=2×2﹣3=1,
∴点(2,1)在该一次函数图象上,选项 A符合题意;
B.当 x=2时,y=2×2﹣3=1,1≠3,
∴点(2,3)不在该一次函数图象上,选项 B不符合题意;
C.当 x=﹣1时,y=2×(﹣1)﹣3=﹣5,﹣5≠1,
∴点(﹣1,1)不在该一次函数图象上,选项 C不符合题意;
D.当 x=1时,y=2×1﹣3=﹣1,﹣1≠5,
∴点(1,5)不在该一次函数图象上,选项 D不符合题意.
故选:A.
【点评】本题考查了一次函数图象上点的坐标特征,利用一次函数图象上点的坐标特征,
求出 b值是解题的关键.
5.(3分)下列说法正确的是( )
A.0.2是 0.4的算术平方根
B.﹣5是 25的平方根
C. 的算术平方根是 9
D.16的平方根是 4
【分析】根据算术平方根及平方根的定义逐项判断即可.
【解答】解:0.2是 0.04的算术平方根,则 A不符合题意;
﹣5是 25的平方根,则 B符合题意;
=9,其算术平方根是 3,则 C不符合题意;
16的平方根是±4,则 D不符合题意;
故选:B.
【点评】本题考查平方根及算术平方根,熟练掌握相关定义是解题的关键.
6.(3分)如图,在平面直角坐标系中,△ABC与△A'B'C'关于 x轴对称,其中点 A,B,C
的对应点分别为点 A',B',C',若点 P(2,3)在△ABC的边上,则点 P在△A'B'C'上的
对应点 P'的坐标是( )
A.(3,2) B.(﹣2,3) C.(2,﹣3) D.(﹣2,﹣3)
【分析】利用关于 x轴的对称点的坐标特点可得答案.
【解答】解:∵△ABC与△A'B'C'关于 x轴对称,点 P(2,3)在△ABC的边上,
∴点 P在△A'B'C'上的对应点 P'的坐标是(2,﹣3).
故选:C.
【点评】此题主要考查了关于 x轴的对称点的坐标,关键是掌握关于 x轴的对称点的坐
标特点:横坐标不变,纵坐标互为相反数.
7.(3分)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读 kǔn,门槛的
意思)一尺,不合二寸,问门广几何?题目大意是:如图 1、2(图 2为图 1的平面示意
图),推开双门,双门间隙 CD的距离为 2寸,点 C和点 D距离门槛 AB都为 1尺(1尺
=10寸),则 AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
【分析】取 AB的中点 O,过 D作 DE⊥AB于 E,根据勾股定理解答即可得到结论.
【解答】解:取 AB的中点 O,过 D作 DE⊥AB于 E,如图 2所示:
由题意得:OA=OB=AD=BC,
设 OA=OB=AD=BC=r寸,
则 AB=2r(寸),DE=10(寸),OE= CD=1(寸),AE=(r﹣1)寸,
在 Rt△ADE中,AE2+DE2=AD2,
即(r﹣1)2+102=r2,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸,
故选:C.
【点评】本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.
8.(3分)对于一次函数 y=kx+b(k≠0),根据两位同学的对话信息,下列结论一定正确的
是( )
A.y随 x的增大而增大
B.函数图象与 y轴的交点位于 x轴下方
C.k﹣b<0
D.k+b>0
【分析】根据一次函数的性质以及一次函数图象上点的坐标特征判断即可.
【解答】解:∵一次函数 y=kx+b(k≠0)的图象不经过第三象限,
∴一次函数 y=kx+b(k≠0)的图象经过经过第二、四象限或第一、二、四象限,
∴k<0,
∴y随 x的增大而减小,故 A错误,不合题意;
又∵函数图象经过点(0,3),
∴函数图象与 y轴的交点位于 x轴上方,故 B错误,不合题意;
∵k<0,b=3>0,
∴k﹣b<0,故选项 C正确,符合题意;
k+b不一定大于 0,故选项 D错误,不合题意.
故选:C.
【点评】本题考查一次函数的图象及性质;熟练掌握一次函数解析式 y=kx+b中,k与 b
对函数图象的影响是解题的关键.
二、填空题(本大题共 8 小题,每小题 3 分,共 24 分)
9.(3分) 的相反数是 4 .
【分析】先求出 的值,再求出相反数即可.
【解答】解:由立方根的计算方法可知 =﹣4,
因为﹣4的相反数为 4,
所以 的相反数为 4.
故答案为:4.
【点评】本题主要考查了相反数和立方根的有关知识.
10.(3分)已知一次函数 y=kx+3(k≠0),其函数值 y随 x值的增大而增大.当 x=﹣2时,
函数值 y可以是 1(答案不唯一) (请写出一个你认为正确的即可).
【分析】由函数值 y随 x值的增大而增大,可得出 k>0,取 k=1,再代入 x=﹣2,求出
y值即可.
【解答】解:∵一次函数 y=kx+3(k≠0),其函数值 y随 x值的增大而增大,
∴k>0,
取 k=1,则一次函数解析式为 y=x+3.
当 x=﹣2时,y=﹣2+3=1.
故答案为:1(答案不唯一).
【点评】本题考查了一次函数图象上点的坐标特征以及一次函数的性质,利用一次函数
的性质,找出 k的取值范围是解题的关键.
11.(3分)如图,正方形的面积为 12,则与该正方形的边长最接近的整数是 3 .
【分析】由于正方形的面积为 12,利用算术平方根的定义可得到正方形的边长为 ,
根据 9<12<16可得到与 最接近的整数为 3.
【解答】解:∵正方形的面积为 12,
∴正方形的边长为 ,
∵9<12<16,
∴3< <4,
∵9<12<12.25,
∴3< <3.5,
∴ 最接近的整数为 3.
故答案为:3.
【点评】本题考查了估算无理数的大小,算术平方根.能够正确估算无理数的大小:利
用完全平方数和算术平方根对无理数的大小进行估算是解题的关键.
12.(3 分)已知一次函数 y=ax﹣5 的图象经过点 A(﹣4,3),则关于 x的一元一次方程
ax﹣5=3的解为 x=﹣4 .
【分析】由一次函数 y=ax﹣5的图象经过点 A(﹣4,3)可知,x=﹣4时,函数 y=3,
即 ax﹣5=3,从而得到关于 x的一元一次方程 ax﹣5=3的解为 x=﹣4.
【解答】解:∵一次函数 y=ax﹣5的图象经过点 A(﹣4,3),
∴于 x的一元一次方程 ax﹣5=3的解为 x=﹣4.
故答案为:x=﹣4.
【点评】本题考查了一次函数与一元一次方程,属于基础题,关键是掌握用数形结合的
方法解题.
13.(3分)如图,在四边形 ABCD中,∠ABC=∠CDA=90°,分别以四边形 ABCD的四
条边为边长,向外作四个正方形,面积分别为 S1,S2,S3,S4.若 S1=6,S2=10,S3=
12,则 S4的值为 16 .
【分析】连接 AC,根据 S4=S2+S3﹣S1即可得出结果.
【解答】解:如图,连接 AC,
∵S1=6,S2=10,S3=12,
∴AD2=6,AB2=10,BC2=12,
在 Rt△ABC与 Rt△ADC中,由勾股定理得,
AC2=AB2+BC2=22,
CD2=AC2﹣AD2,
∴CD2=22﹣6=16,
∴S4=16,
故答案为:16.
【点评】本题考查了勾股定理,正确得出 S4=S2+S3﹣S1是解题的关键.
14.(3 分)在同一直角坐标系中,直线 y1=3x+1 与 x轴,y轴分别交于 A,B两点,直线
y2=kx+b与 x轴,y轴分别交于 C,D两点.若 AB∥CD,点 D在点 B的下方,并且 BD
=6,则直线 y2的表达式为 y2=3x﹣5 .
【分析】由题意可知,将直线 y1=3x+1向下平移 6个单位得到直线 y2.
【解答】解:由题意可知将直线 y1=3x+1向下平移 6个单位得到直线 y2,
故直线 y2的表达式为 y2=3x+1﹣6=3x﹣5.
故答案为:y2=3x﹣5.
【点评】本题考查的是一次函数图象上点的坐标特征,能够明确题意,利用“上加下减”
的平移原则是解答此题的关键.
15.(3分)如图,在直角坐标系中,长方形 OABC的顶点 A,C分别在 x轴,y轴上,点 A,
C的坐标分别为(﹣7,0),(0,4).E为边 BC上一点,点 D的坐标为(﹣5,0),若
△ODE是腰长为 5的等腰三角形,则点 E的坐标是 (﹣2,4)或(﹣3,4) .
【分析】分两种情况讨论,一是 DE=OD=5,作 DF⊥x轴交 BC于点 F,则 F(﹣5,4),
∠DFE=90°,由勾股定理得 EF= =3,则 CE=CF﹣EF=2,所以 E(﹣2,
4);二是 OE=OD=5,则 CE= =3,所以 E(﹣3,4),于是得到问题的答
案.
【解答】解:∵四边形 OABC是矩形,A(﹣7,0),C(0,4),
∴OC=4,BC=OA=7,BC∥x轴,∠OCB=90°,
∵E为边 BC上一点,
∴点 E的纵坐标为 4,
∵D(﹣5,0),△ODE是腰长为 5的等腰三角形,
∴DE=OD=5或 OE=OD=5,
如图 1,DE=OD=5,
作 DF⊥x轴交 BC于点 F,则 F(﹣5,4),∠DFE=90°,
∴CF=5,DF=4,
∴EF= = =3,
∴CE=CF﹣EF=5﹣3=2,
∴E(﹣2,4);
如图 2,OE=OD=5,则 CE= = =3,
∴E(﹣3,4),
综上所述,点 E的坐标是(﹣2,4)或(﹣3,4),
故答案为:(﹣2,4)或(﹣3,4).
【点评】此题重点考查图形与坐标、矩形的性质、等腰三角形的判定、勾股定理、数形
结合与分类讨论数学思想的运用等知识与方法,正确地作出辅助线构造直角三角形是解
题的关键.
16.(3 分)皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的
面积 ,其中 N,L分别表示这个多边形内部与边界上的格点个数.在平面直
角坐标系中,横、纵坐标都是整数的点为格点.已知 A(0,8),B(4,4),则△AOB内
部的格点个数是 9 .
【分析】根据皮克定理及三角形边界上的格点的个数,可列出关于 N,L的二元一次方程
组,解之即可得出结论.
【解答】解:∵点 A的坐标为(0,8),点 B的坐标为(4,4),
∴△AOB的面积为 ×8×4=16,
即 N+ L﹣1=16①;
∵边 OA上的格点数是 9,边 OB上的格点数是 5,边 AB上的格点数是 5,
∴L=9+5+5﹣3②.
联立①②组成方程组得: ,
解得: ,
∴△AOB内部的格点个数是 9.
故答案为:9.
【点评】本题考查了二元一次方程组的应用以及坐标与图形性质,找准等量关系,正确
列出二元一次方程组是解题的关键.
三、解答题(本大题共 8 小题,共 72 分)
17.(16分)计算:
(1) ;
(2) ;
(3) ;
(4) .
【分析】(1)根据二次根式的性质化简,再合并同类二次根式即可;
(2)先计算乘法,再计算除法即可;
(3)先计算二次根式的除法,再计算加法即可;
(4)先计算二次根式的除法,再计算减法即可.
【解答】解:(1)
=6 ﹣4
=2 ;
(2)
=
=
=2;
(3)
= +
=2 +
= ;
(4)
= ﹣ ﹣1
=3﹣2﹣1
=0.
【点评】本题考查二次根式的混合运算,熟练掌握相关运算法则是解题的关键.
18.(4分)围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有 4000多年的历史.如
图是某围棋棋盘的一部分,若棋盘是由边长均为 1的小正方形组成的,棋盘上 A,B两颗
棋子的坐标分别为 A(﹣2,3),B(0,﹣1).
(1)根据题意,画出相应的平面直角坐标系;
(2)有一颗黑色棋子 C的坐标为(2,2),请标注出黑色棋子 C的位置.
【分析】(1)利用 A、B点坐标画出对应的直角坐标系;
(2)根据点的坐标作出点 C的位置即可.
【解答】解:(1)建立如图所示的直角坐标系;
(2)如图,点 C即为所求.
【点评】本题考查坐标确定位置,解题关键是正确作出图形,属于中考常考题型.
19.(6分)把下列各数写入相应的集合中:
,2.5, , ,0, , ,0.5757575…(相邻两个 5 之间 7 的
个数逐次加 1)
(1)有理数集合{ ﹣ ,2.5,( )2,0,﹣ …};
(2)无理数集合{ , ,0.5757575…(相邻两个 5之间 7的个数逐次加 1) …}.
【分析】根据实数的分类及二次根式的性质解答即可.
【解答】解:( )2= ,,﹣ =﹣3,
(1)有理数集合{﹣ ,2.5,( )2,0,﹣ ,...}.
故答案为:﹣ ,2.5,( )2,0,﹣ ;
(2)无理数集合{ , ,0.5757575…(相邻两个 5之间 7的个数逐次加 1),..}
故答案为: , ,0.5757575…(相邻两个 5之间 7的个数逐次加 1).
【点评】本题考查的是实数的分类及二次根式的性质与化简,熟知实数的分类是解题的
关键.
20.(8 分)党的十八大以来,各地积极推动城市绿化工作,大力拓展城市生态空间,让许
多城市再现绿水青山、某小区物业在小区拐角清理出了一块空地进行绿化改造,如图,
∠ABC=90°,AB=12m,BC=9m,AD=17m,CD=8m.
(1)为了方便居民的生活,在绿化时将修一条从点 A直通点 C的小路,求小路 AC的长
度;
(2)若该空地的改造费用为每平方米 150元,试计算改造这片空地共需花费多少元?
【分析】(1)根据勾股定理求出 AC即可;
(2)由勾股定理的逆定理得出三角形 ACD是直角三角,再根据三角形的面积公式求解
即可.
【解答】解:(1)在 Rt△ABC中,由勾股定理得,
AC= = =15(m),
答:小路 AC的长度为 15m;
(2)∵AC2+CD2=152+82=172=AD2,
∴△ACD是直角三角形,
∴S 2四边形 ABCD= = =114(m ),
114×150=17100(元).
答:改造这片空地共需花费 17100元.
【点评】本题考查了勾股定理的应用,熟记勾股定理是解题的关键.
21.(8分)我们知道 是无理数,因此 的小数部分我们不可能全部写出来,于是小明
用 来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是
有道理的,因为 的整数部分是 1,将这个数减去其整数部分,差就是小数部分.又例
如: ,即 ,所以 的整数部分为 2,小数部分为 .请
根据以上信息,回答下列问题:
(1) 整数部分是 5 ,小数部分是 ﹣5 ;
(2)如果 的整数部分为 a, 的整数部分为 b,求 12a+7b的立方根;
(3)已知 ,其中 x是整数,且 0<y<1,求 x+y的值.
【分析】(1)估算出 在哪两个连续整数之间即可;
(2)分别估算出 及 在哪两个连续整数之间后即可求得 a,b的值,然后将其代
入 12a+7b中计算,最后根据立方根的定义即可求得答案;
(3)估算出 9﹣ 的范围后即可确定 x,y的值,然后将其代入 x+y中计算即可.
【解答】解:(1)∵5< <6,
∴ 的整数部分是 5,小数部分是 ﹣5.
故答案为:5, ﹣5;
(2)∵ 的整数部分为 a,且 3< <4,
∴a=3,
∵ 的整数部分为 b,4< <5,
∴b=4,
∴12a+7b=12×3+7×4=64,
∴12a+7b的立方根是 4.
(3)∵2< <3,
∴6<9﹣ <7,
∵ ,其中 x是整数,且 0<y<1,
∴x=7,y= ﹣2,
∴x+y=7+( ﹣2)=5+ .
则 x+y的值为 5+ .
【点评】本题考查的是无理数的计算,估算无理数的整数部分是解题关键.
22.(8分)在平面直角坐标系中,A,B两点的坐标分别是 A(0,a),B(0,b),且 +|12
﹣b|=0.
(1)求 b﹣a的平方根;
(2)若在 x轴的正半轴上有一点 C,且△ABC的面积是 27,求点 C的坐标;
(3)过(2)中的点 C作直线 MN∥y轴,在直线 MN上是否存在点 D,使得△ACD的
面积是△ABC面积的 ?若存在,请求出点 D的坐标;若不存在,请说明理由.
【分析】(1)根据平方根和绝对值具有非负性即可求出 a,b的值;
(2)假设有一点 C,使得△ABC的面积是 27,AB=18,即可求出三角形的高,从而求
出点 C的坐标;
(3)由(2)知△ABC的面积是 27,则△ACD的面积是 3,由 MN∥y轴得出△ACD的
高是 3,求出底即可求出 C的坐标.
【解答】解:(1)∵ +|12﹣b|=0.
∴a+6=0,12﹣b=0,
∴a=﹣6,b=12,
∴b﹣a=12﹣(﹣6)=18,
∴b﹣a的平方根为±3 ;
(2)由(1)知 A(0,﹣6),B(0,12),
∴AB=18,
∴S△ABC= AB OC= ×18 OC=27,
解得 OC=3,
∵C在 x轴的正半轴上,
∴C的坐标为(3,0);
(3)存在,由(2)知△ABC的面积是 27,
∴△ACD的面积是 3,
∵MN∥y轴,
∴△ACD的高是 3,
∴S△ACD= CD 3=3,
解得 CD=2,
∵C在直线 MN上,
∴C的坐标为(3,2)或(3,﹣2).
【点评】本题考查三角形的面积,平面直角坐标系,平方根和绝对值的性质,熟练掌握
以上知识是解题关键.
23.(10 分)如图,一次函数 y1=ax+b的图象与 y轴负半轴相交于点 A,与正比例函数 y2
=kx的图象交于点 B(﹣8,6),且 .
(1)求正比例函数与一次函数的表达式;
(2)请直接写出当 y1>y2时,x的取值范围.
【分析】(1)利用待定系数法求解即可;
(2)观察图象即可求解.
【解答】解:(1)∵正比例函数 y2=kx的图象过点 B(﹣8,6),
∴6=﹣8k,
∴k=﹣ ,
∴正比例函数的表达式为 y2=﹣ x;
由 B(﹣8,6)可知 OB= =10,
∵ ,
∴OA=5,
∴A(0,﹣5),
把 A、B的坐标代入 y1=ax+b得 ,
解得 ,
∴一次函数的表达式为 y1=﹣ x﹣5;
(2)由图象可知,当 y1>y2时,x的取值范围是 x<﹣8.
【点评】本题考查了一次函数图象上点的坐标特征、待定系数法求一次函数解析式以及
一次函数与不等式,数形结合是解题的关键.
24.(12分)通过小学的学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之
间会产生阻碍物体运动的力、像这样的力是摩擦力.小明利用如图 1所示的装置测量在
不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的
木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到
的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成如表:
砝码的质量 0 50 100 150 200 250
m/g
滑动摩擦力 f/N 1.8 2.0 2.2 2.4 2.6 2.8
(1)请在图 2的平面直角坐标系内,描出六次测量的有序数对(m,f)所对应的六个点;
(2)这些点是否在一条直线上?如果是,请确定 f与 m的关系式;如果不是,请说明理
由;
(3)在某次实验中,测得木块受到的摩擦力为 4.2N,则此时砝码的质量是多少?
(4)在实验过程中,当砝码的质量为 100g~800g时,请直接写出木块受到的摩擦力的
最大值和最小值分别为多少?
【分析】(1)在平面直角坐标系中描点即可;
(2)将(1)中的 6个点连接起来,判断是否为直线.如果是直线,则利用待定系数法
求出 f与 m的关系式即可;
(3)当 f=4.2时,求出对应 m的值即可;
(4)由 f与 m的关系式,确定 f随 m的增减性,根据 m的取值范围,分别求出 f的最大
值和最小值即可.
【解答】解:(1)在平面直角坐标系中六次测量的有序数对(m,f)所对应的六个点如
图所示:
(2)如上图所示,这些点在一条直线上.
设 f与 m的关系式为 f=km+b,将(0,1.8)和(50,2.0)代入,
得 ,解得 ,
∴f与 m的关系式为 f=0.004m+1.8.
(3)当 f=4.2时,0.004m+1.8=4.2,解得 m=600,
∴此时砝码的质量是 600g.
(4)∵f随 m的增大而增大,
∴当 m=800时,f值最大,此时 f=0.004×800+1.8=5.0;
当 m=100时,f值最小,此时 f=0.004×100+1.8=2.2.
∴当砝码的质量为 100g~800g时,木块受到的摩擦力的最大值和最小值分别为 5.0N,
2.2N.
【点评】本题考查函数的表示方法等,利用待定系数法求出函数的解析式是解题的关键.
同课章节目录
