三角形的中位线
图片预览




文档简介
课件24张PPT。欢迎各位领导、贵兵
来我校莅临指导! 1、什么叫做三角形的中线?
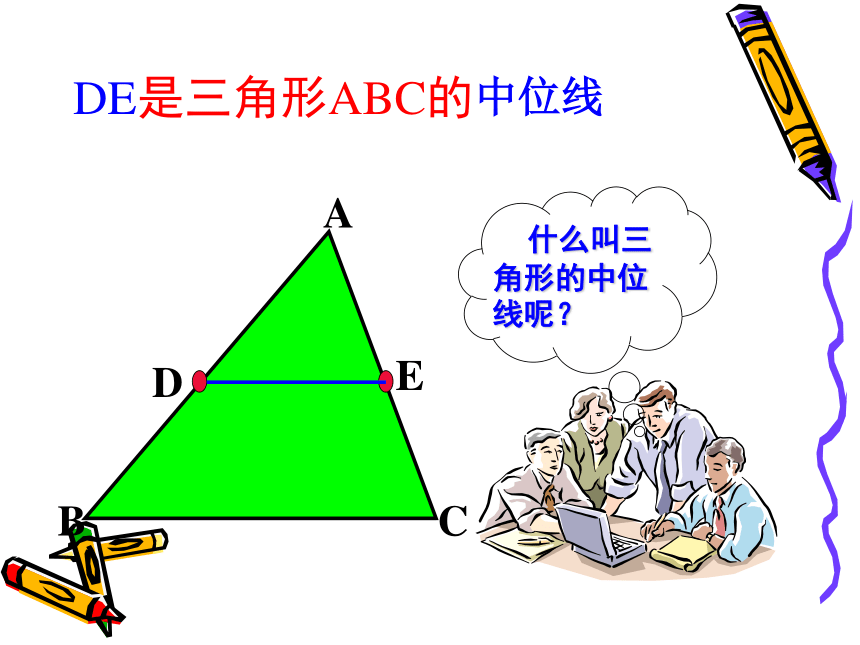
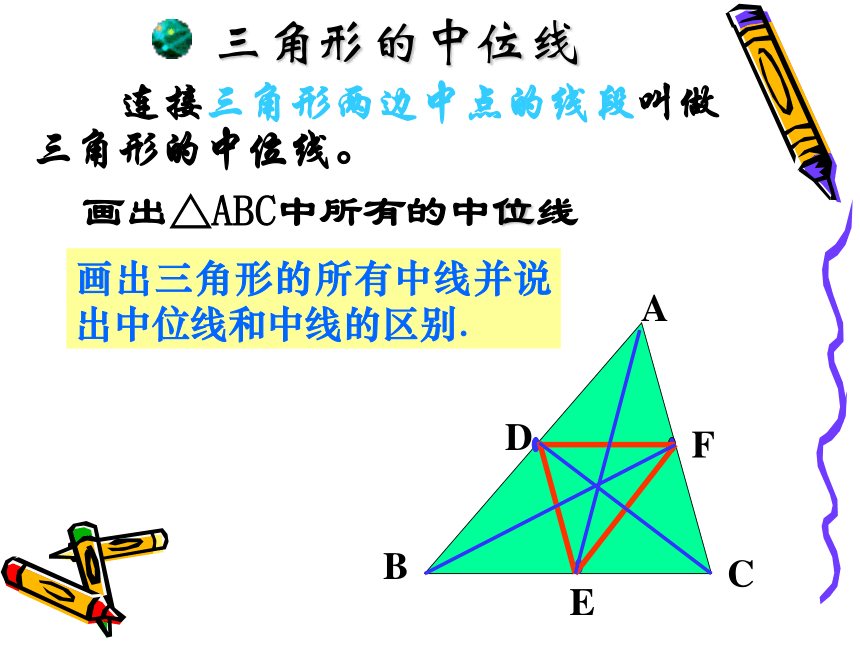
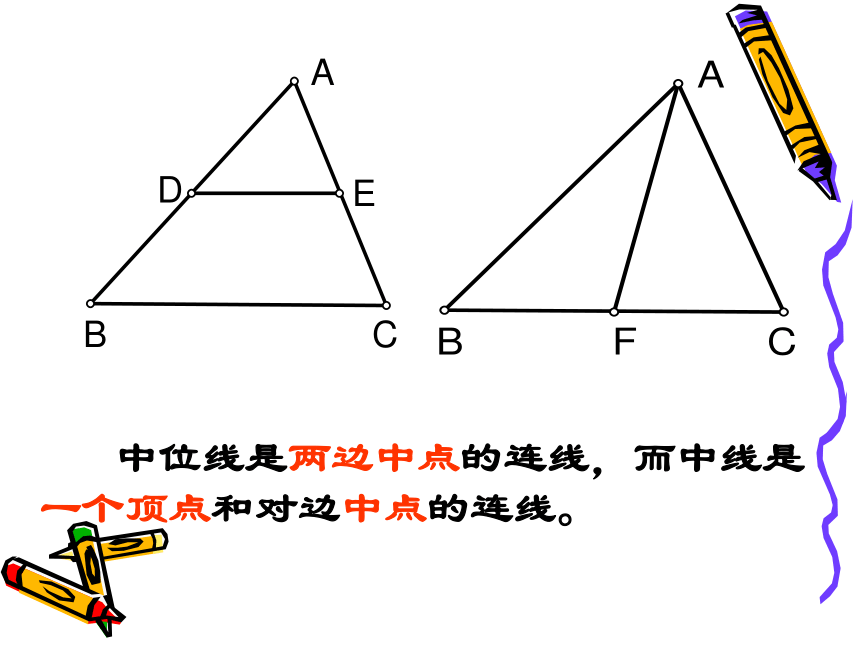
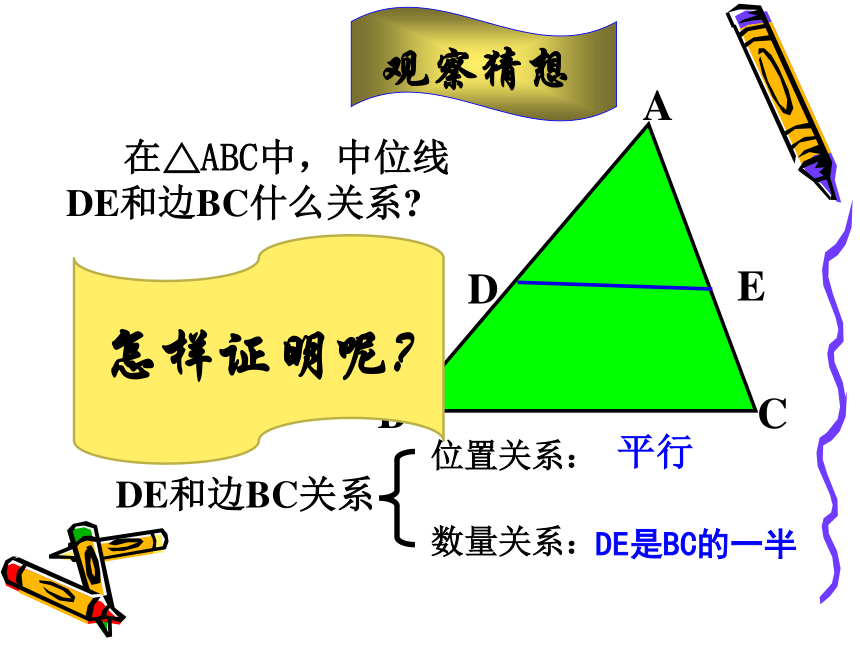
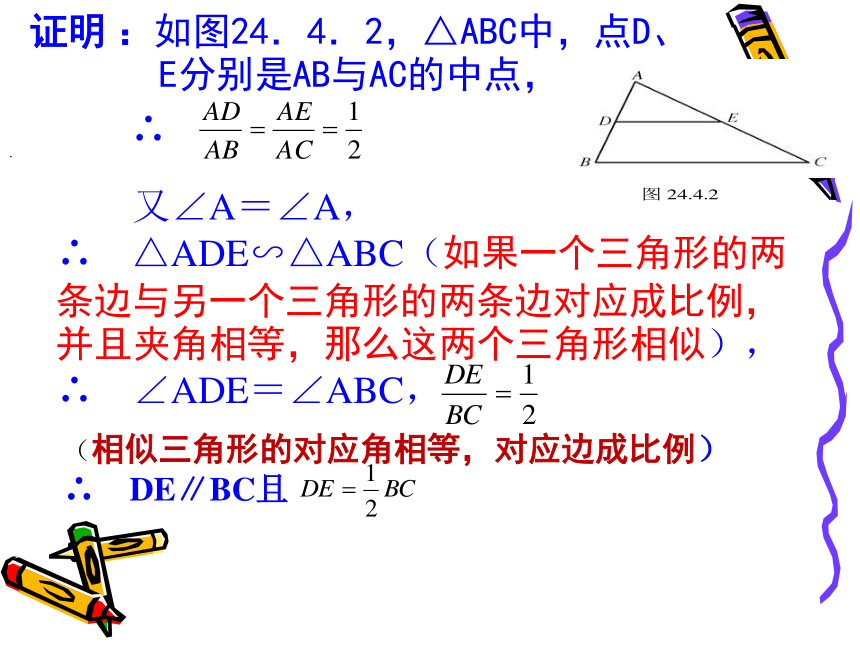
2、三角形相似判定方法有几种? 3、已知D、E是△ABC 中AB、AC边的中点,则DE与BC的位置和大小有什么关系呢?这就是我们今天将要研究的课题 24.4 三角形的中位线DEDE是三角形ABC的中位线三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。画出三角形的所有中线并说出中位线和中线的区别.DEF 中位线是两边中点的连线,而中线是一个顶点和对边中点的连线。观察猜想 在△ABC中,中位线DE和边BC什么关系?DE和边BC关系数量关系:位置关系:DE∥BCDE平行DE是BC的一半证明 :如图24.4.2,△ABC中,点D、 E分别是AB与AC的中点,
又∠A=∠A,
∴ △ADE∽△ABC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似),
∴ ∠ADE=∠ABC,(相似三角形的对应角相等,对应边成比例)
∴ DE∥BC且.∴结论:三角形的中位线平行于第三边,并且等于它的一半.还有其它证明方法吗?说一说分析:延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CFE,
得CF=AE , CF//AB
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
三角形的中位线的性质 三角形的中位线平行于第三边,并且等于它的一半练习 三角形各边的长分别为6 cm、8 cm 和 10 cm ,求连接各边中点所成三角形的周长.AB=10 cmBC=8 cmAC=6 cmEF=5 cmDF=4 cmDE=3 cm(12 cm)大家一起答已知:如图, 在⊿ABC中,AD=BD,AF=CF,BE=CE.
求证:DF与AE互相平分。例1 求证三角形的一条中位线与第三边 上的中线互相平分。证明:连结DE、FE∵AD=BD,BE=CE
∴DE∥AC(三角形中位线定理)同理 EF∥AB所以四边形ADEF是平行四边形所以DF与AE互相平分(平行四边形的性质)例2 如图24.4.4 D、E分别是边BC、AB的中点,AD交CE于G ⊿ABC 中求证:证明:连结DE∵D、E分别是BC、AB的中点
∴DE∥AC (三角形中位线定理)∴ΔACG∽ΔDEG∴∴练习
1.如图,△ABC中,D、E、F分别为BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OA、OF的长度与∠EDF的大小 DE=3cmAB=6 cmBC=10 cmOA=2/3AD
=2/3 X1/2BC
=2/3X1/2X10
=10/3(cm)ABC测出MN的长,就可知A、B两点的距离
MN应用在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.若MN=36 m,则AB=2MN=72 m如果,MN两点之间还有阻隔,你有什么解决办法?怎样求A、B两点间的距离?
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
所以EF//HG,EF=HG
所以四边形EFGH是平行四边形小 结三角形中位线定义三角形中位线定理三角形中位线定理应用三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。DEF三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段①三角形的中位线是三角形中一种重要的线段,它与三角形的中线不同:②理解三角形的中位线定义的两层含义:⑵∵ DE为△ABC的中位线 ⑴∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点③一个三角形共有三条中位线。定义 如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行
② 证明一条线段是另一条线段的2倍或1/2ABCDE 三角形的中位线定理 是三 角形 的一个重要性质定理:
三角形的中位线平行于第三边,并且等于第三边的 一半.
.
定理的主要用途:小结1.三角形的中位线定义.2.三角形的中位线定理.3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.4.线段的倍分要转化为相等问题来解决.5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)再见
来我校莅临指导! 1、什么叫做三角形的中线?
2、三角形相似判定方法有几种? 3、已知D、E是△ABC 中AB、AC边的中点,则DE与BC的位置和大小有什么关系呢?这就是我们今天将要研究的课题 24.4 三角形的中位线DEDE是三角形ABC的中位线三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。画出三角形的所有中线并说出中位线和中线的区别.DEF 中位线是两边中点的连线,而中线是一个顶点和对边中点的连线。观察猜想 在△ABC中,中位线DE和边BC什么关系?DE和边BC关系数量关系:位置关系:DE∥BCDE平行DE是BC的一半证明 :如图24.4.2,△ABC中,点D、 E分别是AB与AC的中点,
又∠A=∠A,
∴ △ADE∽△ABC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似),
∴ ∠ADE=∠ABC,(相似三角形的对应角相等,对应边成比例)
∴ DE∥BC且.∴结论:三角形的中位线平行于第三边,并且等于它的一半.还有其它证明方法吗?说一说分析:延长ED到F,使DF=ED , 连接CF
易证△ADE≌△CFE,
得CF=AE , CF//AB
又可得CF=BE,CF//BE
所以四边形BCFE是平行四边形
则有DE//BC,DE= EF= BC
三角形的中位线的性质 三角形的中位线平行于第三边,并且等于它的一半练习 三角形各边的长分别为6 cm、8 cm 和 10 cm ,求连接各边中点所成三角形的周长.AB=10 cmBC=8 cmAC=6 cmEF=5 cmDF=4 cmDE=3 cm(12 cm)大家一起答已知:如图, 在⊿ABC中,AD=BD,AF=CF,BE=CE.
求证:DF与AE互相平分。例1 求证三角形的一条中位线与第三边 上的中线互相平分。证明:连结DE、FE∵AD=BD,BE=CE
∴DE∥AC(三角形中位线定理)同理 EF∥AB所以四边形ADEF是平行四边形所以DF与AE互相平分(平行四边形的性质)例2 如图24.4.4 D、E分别是边BC、AB的中点,AD交CE于G ⊿ABC 中求证:证明:连结DE∵D、E分别是BC、AB的中点
∴DE∥AC (三角形中位线定理)∴ΔACG∽ΔDEG∴∴练习
1.如图,△ABC中,D、E、F分别为BC、AC、AB的中点,AD、BE、CF相交于点O,AB=6,BC=10,AC=8.试求出线段DE、OA、OF的长度与∠EDF的大小 DE=3cmAB=6 cmBC=10 cmOA=2/3AD
=2/3 X1/2BC
=2/3X1/2X10
=10/3(cm)ABC测出MN的长,就可知A、B两点的距离
MN应用在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.若MN=36 m,则AB=2MN=72 m如果,MN两点之间还有阻隔,你有什么解决办法?怎样求A、B两点间的距离?
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
所以EF//HG,EF=HG
所以四边形EFGH是平行四边形小 结三角形中位线定义三角形中位线定理三角形中位线定理应用三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线。DEF三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段①三角形的中位线是三角形中一种重要的线段,它与三角形的中线不同:②理解三角形的中位线定义的两层含义:⑵∵ DE为△ABC的中位线 ⑴∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点③一个三角形共有三条中位线。定义 如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行
② 证明一条线段是另一条线段的2倍或1/2ABCDE 三角形的中位线定理 是三 角形 的一个重要性质定理:
三角形的中位线平行于第三边,并且等于第三边的 一半.
.
定理的主要用途:小结1.三角形的中位线定义.2.三角形的中位线定理.3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.4.线段的倍分要转化为相等问题来解决.5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)再见
