3.4.1 生产配套和工程问题课件(共30张PPT)【2023秋人教七上数学高效实用备课】
文档属性
| 名称 | 3.4.1 生产配套和工程问题课件(共30张PPT)【2023秋人教七上数学高效实用备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第1课时 生产配套和工程问题
第4节 实际问题与一元一次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解配套问题、工程问题的背景.
2.分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
3.掌握一元一次方程解决实际问题的一般步骤.
学习目标
重点
难点
新课引入
前面我们学习了一元一次方程的解法.本节课,我们将讨论一元一次方程的应用.生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗
例1 某车间有 22 名工人,每人每天可以生产 1200 个螺柱或 2000 个螺母,1 个螺柱需要配 2 个螺母,为使每天生产的螺柱和螺母刚好配套,应安排生产螺柱和螺母的工人各多少名?
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
新知学习
一 配套问题
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
想一想,设哪个量为未知数,使问题解决比较简便呢?
标出未知量
生产螺柱人数 生产螺母人数 螺柱数 螺母数
x 22 - x
1200x
2000(22 - x)
(3) 螺母数 = 螺柱数×2,即 2000(22 - x) = 2×1200x
解:设应安排 x 名工人生产螺柱,则安排 (22 - x) 名工人生产螺母. 根据螺母的数量是螺柱的2倍,列出方程
2000 (22 - x)=2×1200x.
解方程,得 5(22 - x) = 6x,
110 - 5x = 6x,
x = 10.
22 - x = 12.
答:为使每天生产的螺柱和螺母刚好配套,应安排 10 人生产螺柱,12 人生产螺母.
检验:
x = 10 是原方程的解且符合实际意义.
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
生产螺柱人数 生产螺母人数 螺柱数 螺母数
22-y y
解方程得:y = 12,22-y = 10.
1200(22-y)
2000y
(3) 螺母数 = 螺柱数×2,即 2000y = 2×1200(22-y)
归纳
配套问题中的基本关系:
若 m 个 A 和 n 个 B 配成一套,则 ,
可得等量关系:m×B 的数量=n×A 的数量.
归纳
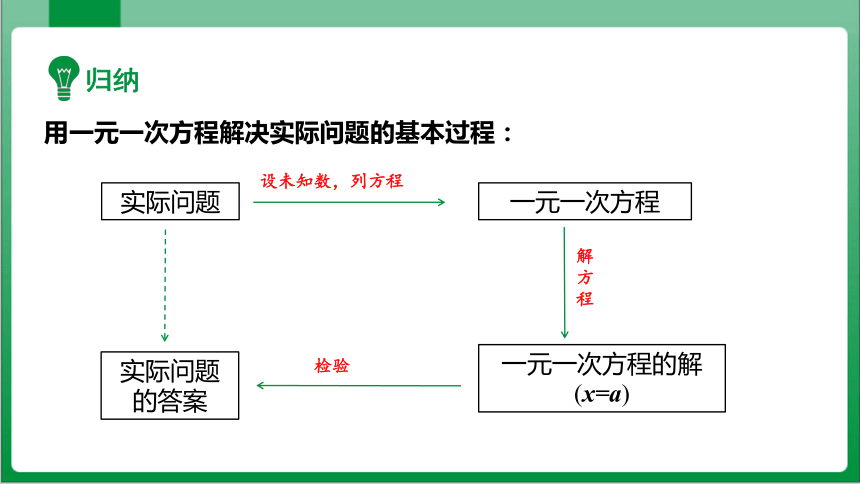
用一元一次方程解决实际问题的基本过程:
实际问题
设未知数,列方程
一元一次方程
解
方
程
一元一次方程的解
(x=a)
检验
实际问题
的答案
这一过程一般包括设、列、解、检、答等步骤,即
(1)设未知数,
(2)列方程,
(3)解方程,
(4)检验所得结果,
(5)确定答案,
正确分析问题中的相等关系是列方程的基础.
针对训练
一套仪器由一个 A 部件和三个 B 部件构成,用 1m3 钢材可做 40 个 A 部件或 240 个 B 部件,现要用 6m3 钢材制作这种仪器,应用多少钢材做A部件,多少钢材做 B 部件,恰好配成这种仪器多少套?
分析:(1) A 部件数 : B 部件数 = 1 : 3;
(2) A 部件数 = A 部件所用钢材×40,
B 部件数 = B 部件所用钢材×240;
(3) A 部件所用钢材 + B 部件所用钢材 = 6.
分析:(1) A 部件数 : B 部件数 = 1 : 3;
(2) A 部件数 = A 部件所用钢材×40,
B 部件数 = B 部件所用钢材×240;
(3) A 部件所用钢材 + B 部件所用钢材 = 6.
标出未知量
分析:(1) A 部件数 : B 部件数 = 1 : 3;
(2) A 部件数 = A 部件所用钢材×40,
B 部件数 = B 部件所用钢材×240;
(3) A 部件所用钢材 + B 部件所用钢材 = 6.
想一想,设哪个量为未知数更合适呢?
A 部件数 B 部件数 A 部件所用钢材 B 部件所用钢材
x 6 - x
40x
240(6 - x)
(3) A 部件数 : B 部件数 = 1 : 3,即 40x : 240(6 - x) = 1 : 3,
或 240(6 - x) = 3×40x.
解:设应用 x m3 钢材做 A 部件,则用 (6 - x)m3 钢材做 B部件,恰好配成这种仪器.依题意,列出方程
240 (6 - x) =3×40x.
解方程,得 2(6 - x) = x,
x = 4,
6 - x = 2. 40×4=160(套)
检验:x = 4 是原方程的解且符合实际意义.
答:应用 4m2 钢材做 A 部件,2m2 钢材做 B 部件恰好配成这种仪器160套.
例2 整理一批图书,由一个人做要 40h 完成. 现计划由一部分人先做 4h,然后增加 2 人与他们一起做 8h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
分析:如果把总工作量设为 1,则人均效率 (一个人 1h 完成的工作量) 为 ,x 人先做 4h 完成的工作量为 ,增加 2 个人后再做 8h 完成的工作量为 ,这两个工作量之和应等于总工作量.
二 工程问题
解:设安排 x 人先做 4h. 根据先后两个时段的工作量之和应等于总工作量, 列出方程 ,
解方程,得: 4x + 8(x + 2) = 40,
4x + 8x + 16 = 40,
12x = 24,
x = 2,
答:应安排 2 人先做 4 h.
分析:全程工作的人工作 12 小时的工作量 + 后增加的两人工作 8 小时的工作量 = 工作总量.
设安排 x 人先工作 4h,
列出方程 .
解方程,得 x = 2.
方法二:
同学们想想,还有其他方法吗?
归纳
1.工程问题一般涉及三个量:工作效率,工作时间,工作量;
2.常见数量关系:
(1) 工作量 = 工作效率×工作时间
(2) 工程问题通常把工作总量设为 1,分析题目得出人均效率;
(3) 合作的效率=各单独做的效率和;
(3) 各部分工作量之和等于总工作量.
一条地下管线由甲工程队单独铺设需要 12 天,由乙工程队单独铺设需要 24 天,如果由这两个工程队从两端同时施工,需要多少天可以铺好这条管线?
分析:如果一件工作需要n个小时完成,那么平均每小时完成的工作量就是 .
平均功效 工时 工作量
甲 x
乙 x
针对训练
解:设要 x 天可以铺好这条管线.
可列方程 ,
解这个方程,得 x = 8 .
答:需要 8 天可以铺好这条管线.
随堂练习
1.某车间有60名工人,生产甲、乙两种零件,每人每天可以生产24个甲种零件或12个乙种零件.已知每2个甲种零件和3个乙种零件配成一套,问应安排多少名工人生产甲种零件,多少名工人生产乙种零件,才能使每天生产的这两种零件刚好配套?
分析:生产甲种零件人数+生产乙种零件人数=60,
甲种零件的数量×3=乙种零件的数量×2
解:设应安排 x 名工人生产甲种零件,则有(60-x)名工人生产乙种零件.
根据题意列方程,得 24x×3=12×(60-x)×2.
解方程, 得 x=l5.
60- x=45.
答:应安排15名工人生产甲种零件,45名工人生产乙种零件.
2.为了保证机场按时通航,通往机场的高速公路需要及时翻修完工,已知甲队单独做需要10天完成,乙队单独做需要15天完成,若甲、乙两队合作5天后,再由乙队单独完成剩余的工作量,共需要多少天?
解:设共需 x 天.
根据甲、乙两队合作5天完成的工作量+乙队单独完成剩余的工作量
=总工作量,列出方程
,
解得 x=7.5.
答:共需要7.5天.
课堂小结
1.用一元一次方程解决实际问题的基本过程:
实际问题
设未知数,列方程
一元一次方程
解
方
程
一元一次方程的解
(x=a)
检验
实际问题
的答案
这一过程一般包括设、列、解、检、答等步骤,即
(1)设未知数,
(2)列方程,
(3)解方程,
(4)检验所得结果,
(5)确定答案,
正确分析问题中的相等关系是列方程的基础.
2.配套问题中的基本关系:
若 m 个 A 和 n 个 B 配成一套,则 ,
可得等量关系:m×B 的数量=n×A 的数量.
3.工程问题一般涉及三个量:工作效率,工作时间,工作量;
常见数量关系:
(1) 工作量 = 工作效率×工作时间
(2) 工程问题通常把工作总量设为 1,分析题目得出人均效率;
(3) 合作的效率=各单独做的效率和;
(3) 各部分工作量之和等于总工作量.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第三章 一元一次方程
第1课时 生产配套和工程问题
第4节 实际问题与一元一次方程
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解配套问题、工程问题的背景.
2.分清有关数量关系,能正确找出作为列方程依据的主要等量关系.
3.掌握一元一次方程解决实际问题的一般步骤.
学习目标
重点
难点
新课引入
前面我们学习了一元一次方程的解法.本节课,我们将讨论一元一次方程的应用.生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗
例1 某车间有 22 名工人,每人每天可以生产 1200 个螺柱或 2000 个螺母,1 个螺柱需要配 2 个螺母,为使每天生产的螺柱和螺母刚好配套,应安排生产螺柱和螺母的工人各多少名?
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
新知学习
一 配套问题
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
想一想,设哪个量为未知数,使问题解决比较简便呢?
标出未知量
生产螺柱人数 生产螺母人数 螺柱数 螺母数
x 22 - x
1200x
2000(22 - x)
(3) 螺母数 = 螺柱数×2,即 2000(22 - x) = 2×1200x
解:设应安排 x 名工人生产螺柱,则安排 (22 - x) 名工人生产螺母. 根据螺母的数量是螺柱的2倍,列出方程
2000 (22 - x)=2×1200x.
解方程,得 5(22 - x) = 6x,
110 - 5x = 6x,
x = 10.
22 - x = 12.
答:为使每天生产的螺柱和螺母刚好配套,应安排 10 人生产螺柱,12 人生产螺母.
检验:
x = 10 是原方程的解且符合实际意义.
分析:(1) 生产螺柱人数 + 生产螺母人数 = 22;
(2) 螺柱数 = 1200×生产螺柱人数
螺母数 = 2000×生产螺母人数;
(3) 螺母数 = 螺柱数×2.
生产螺柱人数 生产螺母人数 螺柱数 螺母数
22-y y
解方程得:y = 12,22-y = 10.
1200(22-y)
2000y
(3) 螺母数 = 螺柱数×2,即 2000y = 2×1200(22-y)
归纳
配套问题中的基本关系:
若 m 个 A 和 n 个 B 配成一套,则 ,
可得等量关系:m×B 的数量=n×A 的数量.
归纳
用一元一次方程解决实际问题的基本过程:
实际问题
设未知数,列方程
一元一次方程
解
方
程
一元一次方程的解
(x=a)
检验
实际问题
的答案
这一过程一般包括设、列、解、检、答等步骤,即
(1)设未知数,
(2)列方程,
(3)解方程,
(4)检验所得结果,
(5)确定答案,
正确分析问题中的相等关系是列方程的基础.
针对训练
一套仪器由一个 A 部件和三个 B 部件构成,用 1m3 钢材可做 40 个 A 部件或 240 个 B 部件,现要用 6m3 钢材制作这种仪器,应用多少钢材做A部件,多少钢材做 B 部件,恰好配成这种仪器多少套?
分析:(1) A 部件数 : B 部件数 = 1 : 3;
(2) A 部件数 = A 部件所用钢材×40,
B 部件数 = B 部件所用钢材×240;
(3) A 部件所用钢材 + B 部件所用钢材 = 6.
分析:(1) A 部件数 : B 部件数 = 1 : 3;
(2) A 部件数 = A 部件所用钢材×40,
B 部件数 = B 部件所用钢材×240;
(3) A 部件所用钢材 + B 部件所用钢材 = 6.
标出未知量
分析:(1) A 部件数 : B 部件数 = 1 : 3;
(2) A 部件数 = A 部件所用钢材×40,
B 部件数 = B 部件所用钢材×240;
(3) A 部件所用钢材 + B 部件所用钢材 = 6.
想一想,设哪个量为未知数更合适呢?
A 部件数 B 部件数 A 部件所用钢材 B 部件所用钢材
x 6 - x
40x
240(6 - x)
(3) A 部件数 : B 部件数 = 1 : 3,即 40x : 240(6 - x) = 1 : 3,
或 240(6 - x) = 3×40x.
解:设应用 x m3 钢材做 A 部件,则用 (6 - x)m3 钢材做 B部件,恰好配成这种仪器.依题意,列出方程
240 (6 - x) =3×40x.
解方程,得 2(6 - x) = x,
x = 4,
6 - x = 2. 40×4=160(套)
检验:x = 4 是原方程的解且符合实际意义.
答:应用 4m2 钢材做 A 部件,2m2 钢材做 B 部件恰好配成这种仪器160套.
例2 整理一批图书,由一个人做要 40h 完成. 现计划由一部分人先做 4h,然后增加 2 人与他们一起做 8h,完成这项工作. 假设这些人的工作效率相同,具体应先安排多少人工作?
分析:如果把总工作量设为 1,则人均效率 (一个人 1h 完成的工作量) 为 ,x 人先做 4h 完成的工作量为 ,增加 2 个人后再做 8h 完成的工作量为 ,这两个工作量之和应等于总工作量.
二 工程问题
解:设安排 x 人先做 4h. 根据先后两个时段的工作量之和应等于总工作量, 列出方程 ,
解方程,得: 4x + 8(x + 2) = 40,
4x + 8x + 16 = 40,
12x = 24,
x = 2,
答:应安排 2 人先做 4 h.
分析:全程工作的人工作 12 小时的工作量 + 后增加的两人工作 8 小时的工作量 = 工作总量.
设安排 x 人先工作 4h,
列出方程 .
解方程,得 x = 2.
方法二:
同学们想想,还有其他方法吗?
归纳
1.工程问题一般涉及三个量:工作效率,工作时间,工作量;
2.常见数量关系:
(1) 工作量 = 工作效率×工作时间
(2) 工程问题通常把工作总量设为 1,分析题目得出人均效率;
(3) 合作的效率=各单独做的效率和;
(3) 各部分工作量之和等于总工作量.
一条地下管线由甲工程队单独铺设需要 12 天,由乙工程队单独铺设需要 24 天,如果由这两个工程队从两端同时施工,需要多少天可以铺好这条管线?
分析:如果一件工作需要n个小时完成,那么平均每小时完成的工作量就是 .
平均功效 工时 工作量
甲 x
乙 x
针对训练
解:设要 x 天可以铺好这条管线.
可列方程 ,
解这个方程,得 x = 8 .
答:需要 8 天可以铺好这条管线.
随堂练习
1.某车间有60名工人,生产甲、乙两种零件,每人每天可以生产24个甲种零件或12个乙种零件.已知每2个甲种零件和3个乙种零件配成一套,问应安排多少名工人生产甲种零件,多少名工人生产乙种零件,才能使每天生产的这两种零件刚好配套?
分析:生产甲种零件人数+生产乙种零件人数=60,
甲种零件的数量×3=乙种零件的数量×2
解:设应安排 x 名工人生产甲种零件,则有(60-x)名工人生产乙种零件.
根据题意列方程,得 24x×3=12×(60-x)×2.
解方程, 得 x=l5.
60- x=45.
答:应安排15名工人生产甲种零件,45名工人生产乙种零件.
2.为了保证机场按时通航,通往机场的高速公路需要及时翻修完工,已知甲队单独做需要10天完成,乙队单独做需要15天完成,若甲、乙两队合作5天后,再由乙队单独完成剩余的工作量,共需要多少天?
解:设共需 x 天.
根据甲、乙两队合作5天完成的工作量+乙队单独完成剩余的工作量
=总工作量,列出方程
,
解得 x=7.5.
答:共需要7.5天.
课堂小结
1.用一元一次方程解决实际问题的基本过程:
实际问题
设未知数,列方程
一元一次方程
解
方
程
一元一次方程的解
(x=a)
检验
实际问题
的答案
这一过程一般包括设、列、解、检、答等步骤,即
(1)设未知数,
(2)列方程,
(3)解方程,
(4)检验所得结果,
(5)确定答案,
正确分析问题中的相等关系是列方程的基础.
2.配套问题中的基本关系:
若 m 个 A 和 n 个 B 配成一套,则 ,
可得等量关系:m×B 的数量=n×A 的数量.
3.工程问题一般涉及三个量:工作效率,工作时间,工作量;
常见数量关系:
(1) 工作量 = 工作效率×工作时间
(2) 工程问题通常把工作总量设为 1,分析题目得出人均效率;
(3) 合作的效率=各单独做的效率和;
(3) 各部分工作量之和等于总工作量.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
