湖北省武汉市常青联合体2023-2024学年高二上学期期中联考数学试题(含答案)
文档属性
| 名称 | 湖北省武汉市常青联合体2023-2024学年高二上学期期中联考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 11:55:29 | ||
图片预览




文档简介
武汉市常青联合体2023-2024学年高二上学期期中联考
数学试卷
考试时间:2023年11月16日试 卷满分:150分
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),满分100分,考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号等填写在答题卡上,并用铅笔在答题卡上的相应位置填涂.
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号.
3.回答第Ⅱ卷时,必须用黑色字迹的钢笔或签字笔作答,答案必须写在答卷各题目指定区域内,不准使用铅笔和涂改液.不按以上要求作答的答案无效.
第Ⅰ卷
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某中学高三年级共有学生900人,为了解他们视力状况,用分层抽样的方法从中抽取一个容量为45的样本,若样本中共有女生11人,该校高三年级共有男生( )人
A.220 B.225 C.680 D.685
2.方程表示圆,则的范围是( )
A. B. C. D.
3.已知直线:,:互相垂直,则实数的值为( )
A.3 B.3或1 C.1 D.或
4.如图,空间四边形中,,,,点在上,且,,则( )
A. B.
C. D.
5.直线的倾斜角是( )
A.41° B.49° C.131° D.139°
6.四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果,可以判断出一定没有点数6出现的是( )
A.中位数为3,众数为2 B.平均数为2,方差为3.1
C.中位数为3,方差为1.6 D.平均数为3,中位数为2
7.柏拉图多面体是柏拉图及其追随者对正多面体进行系统研究后而得名的几何体.下图是棱长均为1的柏拉图多面体,,,,分别为,,,的中点,则( )
A. B. C. D.
8.已知三棱锥的体积为15,是空间中一点,,则三棱锥的体积是( )
A.7 B.8 C.9 D.10
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.下列说法,不正确的是( )
A.在空间直角坐标系中,是坐标平面的一个法向量
B.若是直线的方向向量,则()也是直线的方向向量
C.若为空间的一个基底,则构成空间的另一个基底
D.对空间任意一点和不共线的三点,,,若,则,,,四点共面
10.从装有2个红球和3个白球的口袋内任取两个球,则下列选项中的两个事件为不是互斥事件的是( )
A.至多有1个白球;都是红球 B.至少有1个白球;至少有1个红球
C.恰好有1个白球;都是红球 D.至多有1个白球;全是白球
11.如图,在直三棱柱中,,,、分别为,的中点,过点、、作三棱柱的截面,则下列结论中正确的是( )
A.三棱柱外接球的表面积为
B.
C.若交于,则
D.将三棱柱分成体积较大部分和体积较小部分的体积比为13:5
12.已知在平面直角坐标系中,,,动点是平面上动点,其轨迹为.则下列结论正确的是( )
A.若动点满足,则曲线的方程为
B.若动点轨迹为:,则的最小值为10
C.若动点满足,则曲线关于轴对称
D.若动点满足,则面积的最大值为6
第Ⅱ卷
三、填空题(本题共4小题,每小题5分,共20分.请把答案直接填写在答题卡相应位置上.)
13.甲、乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92,则该题被乙独立解出的概率为______.
14.设点、,若直线过点且与线段不相交,则直线的斜率的取值范围是______.
15.若直线:,:()相交于点,过作圆:的切线,切点为,则的最大值为______.
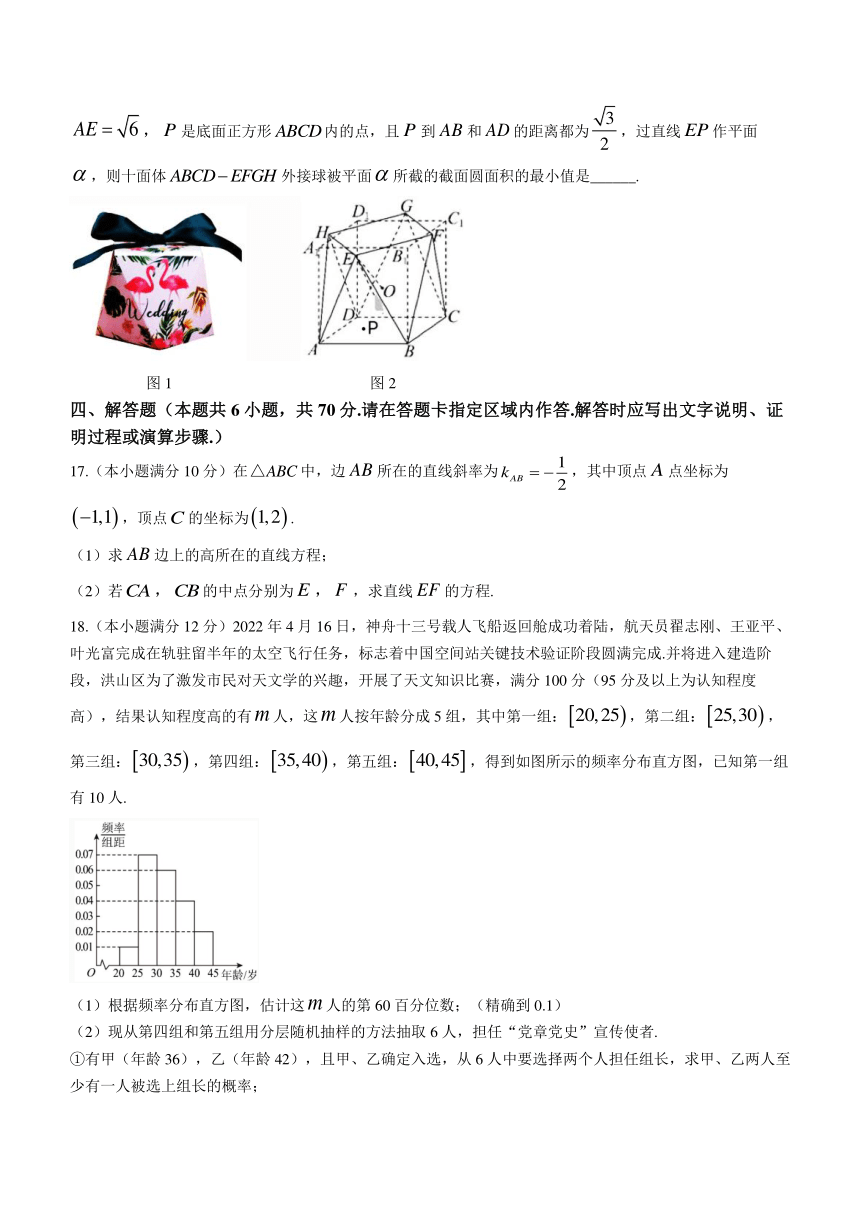
16.数学中有许多形状优美,寓意独特的几何体,图1所示的礼品包装盒就是其中之一,该礼品包装盒可以看成是一个十面体,其中上、下底面为全等的正方形,所有的侧面是全等的三角形.将长方体的上底面绕着其中心旋转60°得到如图2所示的十面体.已知,,是底面正方形内的点,且到和的距离都为,过直线作平面,则十面体外接球被平面所截的截面圆面积的最小值是______.
图1 图2
四、解答题(本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)在中,边所在的直线斜率为,其中顶点点坐标为,顶点的坐标为.
(1)求边上的高所在的直线方程;
(2)若,的中点分别为,,求直线的方程.
18.(本小题满分12分)2022年4月16日,神舟十三号载人飞船返回舱成功着陆,航天员翟志刚、王亚平、叶光富完成在轨驻留半年的太空飞行任务,标志着中国空间站关键技术验证阶段圆满完成.并将进入建造阶段,洪山区为了激发市民对天文学的兴趣,开展了天文知识比赛,满分100分(95分及以上为认知程度高),结果认知程度高的有人,这人按年龄分成5组,其中第一组:,第二组:,第三组:,第四组:,第五组:,得到如图所示的频率分布直方图,已知第一组有10人.
(1)根据频率分布直方图,估计这人的第60百分位数;(精确到0.1)
(2)现从第四组和第五组用分层随机抽样的方法抽取6人,担任“党章党史”宣传使者.
①有甲(年龄36),乙(年龄42),且甲、乙确定入选,从6人中要选择两个人担任组长,求甲、乙两人至少有一人被选上组长的概率;
②若第四组宣传使者的年龄的平均数与方差分别为36和,第五组宣传使者的年龄的平均数与方差分别为42和1,据此估计这人中35~45岁所有人的年龄平均数和方差.
19.(本小题12分)如图,在平行六面体中,,,分别在,,上,且,,.
(1)求证:;
(2)若底面,侧面都是正方形,且二面角的大小为120°,,若是的中点,求的长度.
20.(本小题12分)第19届亚运会2023年9月在杭州市举办,本届亚运会以“绿色、智能、节俭、文明”为办会理念,展示杭州生态之美、文化之韵,充分发挥国际重大赛事对城市发展的牵引作用,从而促进经济快速发展.本次亚运会吉祥物是一组名为“江南忆”的机器人.三个吉祥物分别取名“琮琮”、“莲莲”和“宸宸”,分别代表世界遗产“良渚古城遗址”、“西湖”、“京杭大运河”.亚运期间,篮球比赛间隙安排了机器人吉祥物表演,由后台志愿者操控,,三个开关,分别可操控“琮琮”、“莲莲”和“宸宸”,当闭合时“琮琮”、“莲莲”表演;当闭合时“莲莲”和“宸宸”表演;当闭合时“琮琮”和“宸宸”表演,若,,三个开关闭合的概率分别为,,,且相互独立.
(1)求机器人“琮琮”表演的概率;
(2)求机器人“莲莲”和“宸宸”都表演的概率.
21.(本小题12分)在三棱锥中,底面为等腰直角三角形,.
(1)求证:;
(2)若,,求平面与平面夹角的余弦值.
22.(本小题12分)如图,已知圆:与轴交于,两点,圆过,两点,且直线恰与圆相切.
(1)求圆的方程;
(2)若圆上有一动点,直线与圆的另一个交点为,在平面内是否存在定点,使得始终成立?若存在,求出定点的坐标;若不存在,说明理由.
武汉市常青联合体2023-2024学年高二上学期期中联考
数学参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1 2 3 4 5 6 7 8
C B A C D B A C
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.BD 10.AB 11.AD 12.BCD
三、填空题:本题共4小题,每小题5分,共20分.
13.0.8 14. 15.7 16.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
【详解】(1)由题意知边上的高过,,
因为边上的高所在的直线与所在的直线互相垂直,
故高线的斜率为2,
所以边上的高所在的直线方程为:,即;
(2)由已知点坐标为,,故的中点为,
是的一条中位线,所以,
而,所以直线的斜率为,
所以直线的方程为:
化简可得:.
18.(12分)
【解】(1)设第60百分位数为,
∵,,
∴位于第三组:内;
(2)①由题意得,第四组和第五组抽取人数之比为,即第四组4人,记为,,,甲,第五组2,记为,乙,
对应的样本空间为:,,甲,,乙,,甲,,乙,甲,,乙,甲,甲乙,乙,共15个样本点.
设事件为“甲、乙两人至少一人被选上”,
则有甲,乙,甲,乙,甲,乙,甲,甲乙,乙,共有9个样本点.
∴;
②设第四组的宣传使者的年龄平均数分为,方差为,
设第五组的宣传使者的年龄平均数为,方差为,
第四组和第五组所有宣传使者的年龄平均数为,方差为
则,
即第四组和第五组所有宣传使者的年龄平均数为38,
.
即第四组和第五组所有宣传使者的年龄方差为10;
据此估计这人中年龄在35~45岁的所有人的年龄的平均数为38,方差约为10.
19.(12分)
【解答】解(1)在平行六面体中,
∵,,
∴,,,,
∴
∴
(2)由题意可知:,,面面
∴为二面角的平面角,即
在平行六面体中有:
,,,
∵是的中点
∴
,
即.
20.(12分)
【解答】【解】设,,分别为开关,,闭合的概率,
则,,
(1)记“机器人“琮琮”表演”为事件,发生则需要、两个开关至少一个闭合
∴,由于开关闭合相互独立,则
(2)记“机器人“莲莲”和“宸宸”都表演”为事件,分为两类情况:开关闭合;或者开关不闭合,,同时闭合,则:
综上,机器人“琮琮”表演的概率为,机器人“莲莲”和“宸宸”都表演的概率
21.(12分)
【解析】【解】(1)
证明:取的中点为,连结,,
∵,∴,
在和中,,,
∴,∴,
∵的中点为E,∴,
∵,∴面,
∵面,∴
(2)
过作面,垂足为,连接,,∴
∵,,,平面
∴,同理,
∵底面为等腰直角三角形,,,
∴四边形为正方形且边长为.
以为原点,,,分别为,,轴建立空间直角坐标系,则
,,,
∴,,,
设平面的法向量,则,解得,
取,则,,∴,
设平面的法向量,则,解得,
取,则,,∴,
设平面与平面夹角为
∴
故平面与平面夹角的余弦值为.
22.(12分)
【解答】(1)法一:由,令,解得或4.∴
∵圆过,两点,∴可设圆的圆心
直线的方程为:,即
∵直线与圆相切,∴,解得,
∴圆的方程为:
法二:将圆方程写成一般式:,
由题可得:圆可以看成过和轴交点的圆系方程,不妨设方程为:
()
()
则圆心分别为:,
∵直线与圆相切,切点为
∴,即:
∴
∴圆的方程为:
(2)存在,且为.
由题易得直线斜率存在,设直线的方程为:
代入圆的方程可得:
∴,
代入圆的方程可得:
∴,
设,线段的中点
则,∴
化为:
∴
时恒成立
∴在平面内是存在定点使得始终成立.
数学试卷
考试时间:2023年11月16日试 卷满分:150分
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),满分100分,考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号等填写在答题卡上,并用铅笔在答题卡上的相应位置填涂.
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号.
3.回答第Ⅱ卷时,必须用黑色字迹的钢笔或签字笔作答,答案必须写在答卷各题目指定区域内,不准使用铅笔和涂改液.不按以上要求作答的答案无效.
第Ⅰ卷
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某中学高三年级共有学生900人,为了解他们视力状况,用分层抽样的方法从中抽取一个容量为45的样本,若样本中共有女生11人,该校高三年级共有男生( )人
A.220 B.225 C.680 D.685
2.方程表示圆,则的范围是( )
A. B. C. D.
3.已知直线:,:互相垂直,则实数的值为( )
A.3 B.3或1 C.1 D.或
4.如图,空间四边形中,,,,点在上,且,,则( )
A. B.
C. D.
5.直线的倾斜角是( )
A.41° B.49° C.131° D.139°
6.四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果,可以判断出一定没有点数6出现的是( )
A.中位数为3,众数为2 B.平均数为2,方差为3.1
C.中位数为3,方差为1.6 D.平均数为3,中位数为2
7.柏拉图多面体是柏拉图及其追随者对正多面体进行系统研究后而得名的几何体.下图是棱长均为1的柏拉图多面体,,,,分别为,,,的中点,则( )
A. B. C. D.
8.已知三棱锥的体积为15,是空间中一点,,则三棱锥的体积是( )
A.7 B.8 C.9 D.10
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.下列说法,不正确的是( )
A.在空间直角坐标系中,是坐标平面的一个法向量
B.若是直线的方向向量,则()也是直线的方向向量
C.若为空间的一个基底,则构成空间的另一个基底
D.对空间任意一点和不共线的三点,,,若,则,,,四点共面
10.从装有2个红球和3个白球的口袋内任取两个球,则下列选项中的两个事件为不是互斥事件的是( )
A.至多有1个白球;都是红球 B.至少有1个白球;至少有1个红球
C.恰好有1个白球;都是红球 D.至多有1个白球;全是白球
11.如图,在直三棱柱中,,,、分别为,的中点,过点、、作三棱柱的截面,则下列结论中正确的是( )
A.三棱柱外接球的表面积为
B.
C.若交于,则
D.将三棱柱分成体积较大部分和体积较小部分的体积比为13:5
12.已知在平面直角坐标系中,,,动点是平面上动点,其轨迹为.则下列结论正确的是( )
A.若动点满足,则曲线的方程为
B.若动点轨迹为:,则的最小值为10
C.若动点满足,则曲线关于轴对称
D.若动点满足,则面积的最大值为6
第Ⅱ卷
三、填空题(本题共4小题,每小题5分,共20分.请把答案直接填写在答题卡相应位置上.)
13.甲、乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92,则该题被乙独立解出的概率为______.
14.设点、,若直线过点且与线段不相交,则直线的斜率的取值范围是______.
15.若直线:,:()相交于点,过作圆:的切线,切点为,则的最大值为______.
16.数学中有许多形状优美,寓意独特的几何体,图1所示的礼品包装盒就是其中之一,该礼品包装盒可以看成是一个十面体,其中上、下底面为全等的正方形,所有的侧面是全等的三角形.将长方体的上底面绕着其中心旋转60°得到如图2所示的十面体.已知,,是底面正方形内的点,且到和的距离都为,过直线作平面,则十面体外接球被平面所截的截面圆面积的最小值是______.
图1 图2
四、解答题(本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)在中,边所在的直线斜率为,其中顶点点坐标为,顶点的坐标为.
(1)求边上的高所在的直线方程;
(2)若,的中点分别为,,求直线的方程.
18.(本小题满分12分)2022年4月16日,神舟十三号载人飞船返回舱成功着陆,航天员翟志刚、王亚平、叶光富完成在轨驻留半年的太空飞行任务,标志着中国空间站关键技术验证阶段圆满完成.并将进入建造阶段,洪山区为了激发市民对天文学的兴趣,开展了天文知识比赛,满分100分(95分及以上为认知程度高),结果认知程度高的有人,这人按年龄分成5组,其中第一组:,第二组:,第三组:,第四组:,第五组:,得到如图所示的频率分布直方图,已知第一组有10人.
(1)根据频率分布直方图,估计这人的第60百分位数;(精确到0.1)
(2)现从第四组和第五组用分层随机抽样的方法抽取6人,担任“党章党史”宣传使者.
①有甲(年龄36),乙(年龄42),且甲、乙确定入选,从6人中要选择两个人担任组长,求甲、乙两人至少有一人被选上组长的概率;
②若第四组宣传使者的年龄的平均数与方差分别为36和,第五组宣传使者的年龄的平均数与方差分别为42和1,据此估计这人中35~45岁所有人的年龄平均数和方差.
19.(本小题12分)如图,在平行六面体中,,,分别在,,上,且,,.
(1)求证:;
(2)若底面,侧面都是正方形,且二面角的大小为120°,,若是的中点,求的长度.
20.(本小题12分)第19届亚运会2023年9月在杭州市举办,本届亚运会以“绿色、智能、节俭、文明”为办会理念,展示杭州生态之美、文化之韵,充分发挥国际重大赛事对城市发展的牵引作用,从而促进经济快速发展.本次亚运会吉祥物是一组名为“江南忆”的机器人.三个吉祥物分别取名“琮琮”、“莲莲”和“宸宸”,分别代表世界遗产“良渚古城遗址”、“西湖”、“京杭大运河”.亚运期间,篮球比赛间隙安排了机器人吉祥物表演,由后台志愿者操控,,三个开关,分别可操控“琮琮”、“莲莲”和“宸宸”,当闭合时“琮琮”、“莲莲”表演;当闭合时“莲莲”和“宸宸”表演;当闭合时“琮琮”和“宸宸”表演,若,,三个开关闭合的概率分别为,,,且相互独立.
(1)求机器人“琮琮”表演的概率;
(2)求机器人“莲莲”和“宸宸”都表演的概率.
21.(本小题12分)在三棱锥中,底面为等腰直角三角形,.
(1)求证:;
(2)若,,求平面与平面夹角的余弦值.
22.(本小题12分)如图,已知圆:与轴交于,两点,圆过,两点,且直线恰与圆相切.
(1)求圆的方程;
(2)若圆上有一动点,直线与圆的另一个交点为,在平面内是否存在定点,使得始终成立?若存在,求出定点的坐标;若不存在,说明理由.
武汉市常青联合体2023-2024学年高二上学期期中联考
数学参考答案
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1 2 3 4 5 6 7 8
C B A C D B A C
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.BD 10.AB 11.AD 12.BCD
三、填空题:本题共4小题,每小题5分,共20分.
13.0.8 14. 15.7 16.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
【详解】(1)由题意知边上的高过,,
因为边上的高所在的直线与所在的直线互相垂直,
故高线的斜率为2,
所以边上的高所在的直线方程为:,即;
(2)由已知点坐标为,,故的中点为,
是的一条中位线,所以,
而,所以直线的斜率为,
所以直线的方程为:
化简可得:.
18.(12分)
【解】(1)设第60百分位数为,
∵,,
∴位于第三组:内;
(2)①由题意得,第四组和第五组抽取人数之比为,即第四组4人,记为,,,甲,第五组2,记为,乙,
对应的样本空间为:,,甲,,乙,,甲,,乙,甲,,乙,甲,甲乙,乙,共15个样本点.
设事件为“甲、乙两人至少一人被选上”,
则有甲,乙,甲,乙,甲,乙,甲,甲乙,乙,共有9个样本点.
∴;
②设第四组的宣传使者的年龄平均数分为,方差为,
设第五组的宣传使者的年龄平均数为,方差为,
第四组和第五组所有宣传使者的年龄平均数为,方差为
则,
即第四组和第五组所有宣传使者的年龄平均数为38,
.
即第四组和第五组所有宣传使者的年龄方差为10;
据此估计这人中年龄在35~45岁的所有人的年龄的平均数为38,方差约为10.
19.(12分)
【解答】解(1)在平行六面体中,
∵,,
∴,,,,
∴
∴
(2)由题意可知:,,面面
∴为二面角的平面角,即
在平行六面体中有:
,,,
∵是的中点
∴
,
即.
20.(12分)
【解答】【解】设,,分别为开关,,闭合的概率,
则,,
(1)记“机器人“琮琮”表演”为事件,发生则需要、两个开关至少一个闭合
∴,由于开关闭合相互独立,则
(2)记“机器人“莲莲”和“宸宸”都表演”为事件,分为两类情况:开关闭合;或者开关不闭合,,同时闭合,则:
综上,机器人“琮琮”表演的概率为,机器人“莲莲”和“宸宸”都表演的概率
21.(12分)
【解析】【解】(1)
证明:取的中点为,连结,,
∵,∴,
在和中,,,
∴,∴,
∵的中点为E,∴,
∵,∴面,
∵面,∴
(2)
过作面,垂足为,连接,,∴
∵,,,平面
∴,同理,
∵底面为等腰直角三角形,,,
∴四边形为正方形且边长为.
以为原点,,,分别为,,轴建立空间直角坐标系,则
,,,
∴,,,
设平面的法向量,则,解得,
取,则,,∴,
设平面的法向量,则,解得,
取,则,,∴,
设平面与平面夹角为
∴
故平面与平面夹角的余弦值为.
22.(12分)
【解答】(1)法一:由,令,解得或4.∴
∵圆过,两点,∴可设圆的圆心
直线的方程为:,即
∵直线与圆相切,∴,解得,
∴圆的方程为:
法二:将圆方程写成一般式:,
由题可得:圆可以看成过和轴交点的圆系方程,不妨设方程为:
()
()
则圆心分别为:,
∵直线与圆相切,切点为
∴,即:
∴
∴圆的方程为:
(2)存在,且为.
由题易得直线斜率存在,设直线的方程为:
代入圆的方程可得:
∴,
代入圆的方程可得:
∴,
设,线段的中点
则,∴
化为:
∴
时恒成立
∴在平面内是存在定点使得始终成立.
同课章节目录
