北师大版初中数学九年级下册1.3 三角函数的计算同步课件(共34张PPT)
文档属性
| 名称 | 北师大版初中数学九年级下册1.3 三角函数的计算同步课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 19:35:33 | ||
图片预览










文档简介
(共34张PPT)
北师大版 数学 九年级下册
1.3三角函数的计算
学习目标
1.学会利用计算器求三角函数值并进行相关计算. 2.学会利用计算器根据三角函数值求锐角度数并计算.
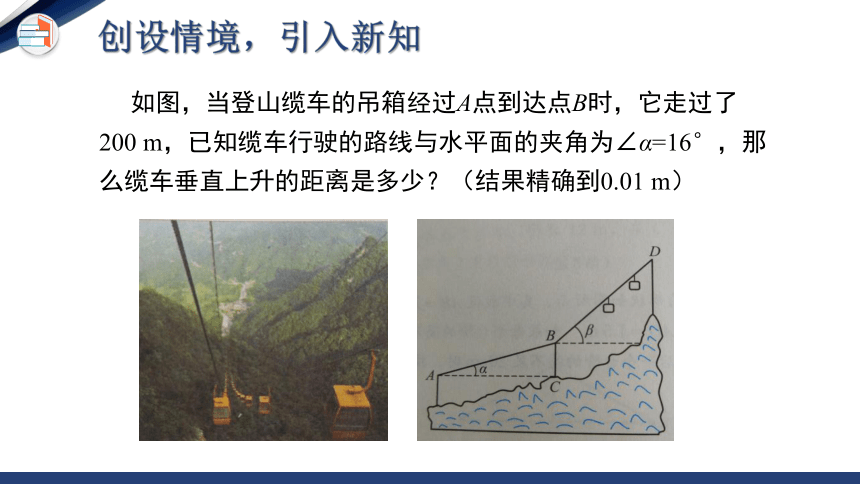
如图,当登山缆车的吊箱经过A点到达点B时,它走过了200 m,已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
创设情境,引入新知
观察下图中的科学计算器,试着熟悉科学计算器的基本操作.
创设情境,引入新知
核心知识点一:
用计算器求三角函数值
在Rt△ABC中,∠ACB=90°,BC=ABsin 16°=200sin 16°.
你知道sin 16°是多少吗?
我们可以借助科学计算器求锐角的三角函数值.
怎样用科学计算器求三角函数值呢?
自主合作,探究新知
你知道sin16°等于多少吗
需要用科学计算器来进行计算.
自主合作,探究新知
用科学计算器求锐角的三角函数值,要用到以下按键:
sin
sin-1 D
cos
cos-1 E
tan
tan-1 F
自主合作,探究新知
例如,求sin16°的按键顺序:
sin
sin1
sin16
0.275 637 355 8
自主合作,探究新知
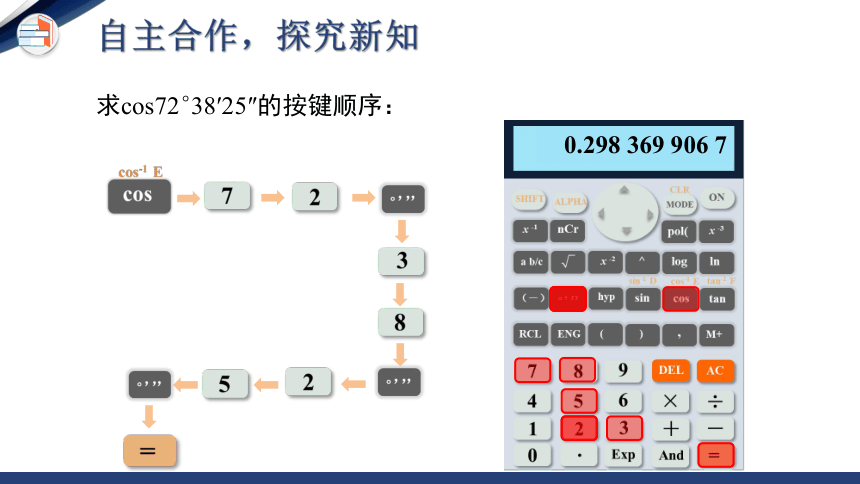
求cos72°38′25″的按键顺序:
cos
cos7
cos72
cos72°
cos72°3
cos72°38
cos72°38′
cos72°38′2
cos72°38′25
cos72°38′25″
0.298 369 906 7
自主合作,探究新知
求tan85°的按键顺序:
tan
tan8
tan85
11.430 052 3
自主合作,探究新知
按键顺序 显示结果
sin16°
cos72 ° 38′25″
tan85°
0.275 637 355 8
0.298 369 906 7
11.430 052 3
计算器的型号与功能可能不同,请按相应的说明书使用.
自主合作,探究新知
例1.如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16 °,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
如图,在Rt△ABC中,∠ACB=90 °,BC=ABsin16 °.
∴BC=200·sin16°≈55.12(m).
典例解析
当缆车继续由点B到达点D时,它又走过了200m,缆车由点B到点D的行驶路线与水平面的夹角为∠β=42 °,由此你还能计算什么
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16 °,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
典例解析
例:用计算器求下列各式的值(精确到0.0001):
(1)sin47°; (2)sin12°30′;
(3)cos25°18′; (4)sin18°+cos55°-tan59°.
解:根据题意用计算器求出:
(1)sin47°≈0.7314;
(2)sin12°30′≈0.2164;
(3)cos25°18′≈0.9041;
(4)sin18°+cos55°-tan59°≈-0.7817.
典例解析
探究新知
核心知识点二:
利用计算器由三角函数值求角度
例2.为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少
如图,在Rt△ABC中,sinA=
那么∠A是多少度呢
要解决这个问题,我们可以借助科学计算器.
探究新知
已知三角函数值求角度,要用到
键的第二功能“sin- ,cos- ,tan- ”和 键。
自主合作,探究新知
例如,已知sinA=0.9816,求∠A的度数
的按键顺序.
sin-1
sin-10
sin-10.
sin-10.9
sin-10.98
sin-10.981
sin-10.9816
78.991 840 39
自主合作,探究新知
已知cosB=0.8607,求∠B的度数
的按键顺序.
cos-1
cos-10
cos-10.
cos-10.8
cos-10.86
cos-10.860
cos-10.8607
30.604 730 07
自主合作,探究新知
已知tanC=56.78,求∠C的度数的按键顺序.
tan-1
tan-15
tan-156
tan-156.
tan-156.7
cos-156.78
88.991 020 49
自主合作,探究新知
按键顺序 显示结果
sinA=0.9816
cosB=0.8607
tanC=56.78
78.991 840 39
30.604 730 07
88.991 020 49
以“度”为单位
再按 键即可显示以“度、分、秒”为单位的结果.
自主合作,探究新知
你能求出∠A的度数了吗
如图,在Rt△ABC中,sinA=
∴∠A
≈14.4775°.
自主合作,探究新知
例:已知下列锐角三角函数值,用计算器求锐角∠A,∠B的度数(结果精确到0.1°):
(1)sinA=0.7,sinB=0.01;
(2)cosA=0.15,cosB=0.8;
(3)tanA=2.4,tanB=0.5.
解:(1)由sinA=0.7,得∠A≈44.4°;由sinB=0.01,得∠B≈0.6°;
(2)由cosA=0.15,得∠A≈81.4°;由cosB=0.8,得∠B≈36.9°;
(3)由tanA=2.4,得∠A≈67.4°;由tanB=0.5,得∠B≈26.6°.
典例解析
cos55°=
cos70°=
cos74°28 '=
tan3°8 ' =
tan80°25'43″=
sin20°=
sin35°=
sin15°32 ' =
0.3420
0.3420
0.5736
0.5736
0.2678
0.2678
5.930
0.0547
角度增大
正弦值增大
余弦值减小
正切值增大
比一比,你能得出什么结论?
自主合作,探究新知
归纳总结
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
归纳总结
1.用计算器计算sin36°18′,按键顺序正确的是( )
D
3
·
sin
1
6
=
A.
8
3
DMS
sin
1
6
=
B.
8
3
DMS
sin
1
6
=
C.
8
2ndf
3
DMS
sin
1
6
=
D.
8
DMS
随堂练习
2.计算器显示结果为sin 0.9816=78.9918的意思正确的是( )
A.计算已知正弦值的对应角度
B.计算已知余弦值的对应角度
C.计算一个角的正弦值
D.计算一个角的余弦值
-1
A
随堂练习
tan26°=
AC
BC
3.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5
若用科学计算器求边AC的长,则下列按键顺序正确的是( )
D
5
÷
tan
2
6
=
A.
A
C
B
5
sin
B.
5
×
cos
C.
5
×
tan
D.
÷
2
6
2
6
2
6
=
=
=
随堂练习
4.已知:sin232°+cos2α=1,则锐角α等于( )
A.32° B.58°
C.68° D.以上结论都不对
A
5.用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin45°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
D
随堂练习
A
6.下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15°
B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15°
D. sin75°﹤sin48°随堂练习
7.如图所示,电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
随堂练习
解析 (1)利用△ABC是等腰直角三角形易得AC的长;
(2)在Rt△BDE中,运用直角三角形的边角关系即可求出BE的长,用AB的长减去BE的长度即可.
随堂练习
三角函数的计算
用计算器求一个锐角三角函数的值
已知锐角的三角函数值求锐角
课堂小结
1、教材“习题1.4”中第1、2、3、5题
2、完成练习册中本课时的练习
作业布置
北师大版 数学 九年级下册
1.3三角函数的计算
学习目标
1.学会利用计算器求三角函数值并进行相关计算. 2.学会利用计算器根据三角函数值求锐角度数并计算.
如图,当登山缆车的吊箱经过A点到达点B时,它走过了200 m,已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
创设情境,引入新知
观察下图中的科学计算器,试着熟悉科学计算器的基本操作.
创设情境,引入新知
核心知识点一:
用计算器求三角函数值
在Rt△ABC中,∠ACB=90°,BC=ABsin 16°=200sin 16°.
你知道sin 16°是多少吗?
我们可以借助科学计算器求锐角的三角函数值.
怎样用科学计算器求三角函数值呢?
自主合作,探究新知
你知道sin16°等于多少吗
需要用科学计算器来进行计算.
自主合作,探究新知
用科学计算器求锐角的三角函数值,要用到以下按键:
sin
sin-1 D
cos
cos-1 E
tan
tan-1 F
自主合作,探究新知
例如,求sin16°的按键顺序:
sin
sin1
sin16
0.275 637 355 8
自主合作,探究新知
求cos72°38′25″的按键顺序:
cos
cos7
cos72
cos72°
cos72°3
cos72°38
cos72°38′
cos72°38′2
cos72°38′25
cos72°38′25″
0.298 369 906 7
自主合作,探究新知
求tan85°的按键顺序:
tan
tan8
tan85
11.430 052 3
自主合作,探究新知
按键顺序 显示结果
sin16°
cos72 ° 38′25″
tan85°
0.275 637 355 8
0.298 369 906 7
11.430 052 3
计算器的型号与功能可能不同,请按相应的说明书使用.
自主合作,探究新知
例1.如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16 °,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
如图,在Rt△ABC中,∠ACB=90 °,BC=ABsin16 °.
∴BC=200·sin16°≈55.12(m).
典例解析
当缆车继续由点B到达点D时,它又走过了200m,缆车由点B到点D的行驶路线与水平面的夹角为∠β=42 °,由此你还能计算什么
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=16 °,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
典例解析
例:用计算器求下列各式的值(精确到0.0001):
(1)sin47°; (2)sin12°30′;
(3)cos25°18′; (4)sin18°+cos55°-tan59°.
解:根据题意用计算器求出:
(1)sin47°≈0.7314;
(2)sin12°30′≈0.2164;
(3)cos25°18′≈0.9041;
(4)sin18°+cos55°-tan59°≈-0.7817.
典例解析
探究新知
核心知识点二:
利用计算器由三角函数值求角度
例2.为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少
如图,在Rt△ABC中,sinA=
那么∠A是多少度呢
要解决这个问题,我们可以借助科学计算器.
探究新知
已知三角函数值求角度,要用到
键的第二功能“sin- ,cos- ,tan- ”和 键。
自主合作,探究新知
例如,已知sinA=0.9816,求∠A的度数
的按键顺序.
sin-1
sin-10
sin-10.
sin-10.9
sin-10.98
sin-10.981
sin-10.9816
78.991 840 39
自主合作,探究新知
已知cosB=0.8607,求∠B的度数
的按键顺序.
cos-1
cos-10
cos-10.
cos-10.8
cos-10.86
cos-10.860
cos-10.8607
30.604 730 07
自主合作,探究新知
已知tanC=56.78,求∠C的度数的按键顺序.
tan-1
tan-15
tan-156
tan-156.
tan-156.7
cos-156.78
88.991 020 49
自主合作,探究新知
按键顺序 显示结果
sinA=0.9816
cosB=0.8607
tanC=56.78
78.991 840 39
30.604 730 07
88.991 020 49
以“度”为单位
再按 键即可显示以“度、分、秒”为单位的结果.
自主合作,探究新知
你能求出∠A的度数了吗
如图,在Rt△ABC中,sinA=
∴∠A
≈14.4775°.
自主合作,探究新知
例:已知下列锐角三角函数值,用计算器求锐角∠A,∠B的度数(结果精确到0.1°):
(1)sinA=0.7,sinB=0.01;
(2)cosA=0.15,cosB=0.8;
(3)tanA=2.4,tanB=0.5.
解:(1)由sinA=0.7,得∠A≈44.4°;由sinB=0.01,得∠B≈0.6°;
(2)由cosA=0.15,得∠A≈81.4°;由cosB=0.8,得∠B≈36.9°;
(3)由tanA=2.4,得∠A≈67.4°;由tanB=0.5,得∠B≈26.6°.
典例解析
cos55°=
cos70°=
cos74°28 '=
tan3°8 ' =
tan80°25'43″=
sin20°=
sin35°=
sin15°32 ' =
0.3420
0.3420
0.5736
0.5736
0.2678
0.2678
5.930
0.0547
角度增大
正弦值增大
余弦值减小
正切值增大
比一比,你能得出什么结论?
自主合作,探究新知
归纳总结
正弦值随着角度的增大(或减小)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大)
正切值随着角度的增大(或减小)而增大(或减小)
归纳总结
1.用计算器计算sin36°18′,按键顺序正确的是( )
D
3
·
sin
1
6
=
A.
8
3
DMS
sin
1
6
=
B.
8
3
DMS
sin
1
6
=
C.
8
2ndf
3
DMS
sin
1
6
=
D.
8
DMS
随堂练习
2.计算器显示结果为sin 0.9816=78.9918的意思正确的是( )
A.计算已知正弦值的对应角度
B.计算已知余弦值的对应角度
C.计算一个角的正弦值
D.计算一个角的余弦值
-1
A
随堂练习
tan26°=
AC
BC
3.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5
若用科学计算器求边AC的长,则下列按键顺序正确的是( )
D
5
÷
tan
2
6
=
A.
A
C
B
5
sin
B.
5
×
cos
C.
5
×
tan
D.
÷
2
6
2
6
2
6
=
=
=
随堂练习
4.已知:sin232°+cos2α=1,则锐角α等于( )
A.32° B.58°
C.68° D.以上结论都不对
A
5.用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin45°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
D
随堂练习
A
6.下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15°
B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15°
D. sin75°﹤sin48°
7.如图所示,电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
随堂练习
解析 (1)利用△ABC是等腰直角三角形易得AC的长;
(2)在Rt△BDE中,运用直角三角形的边角关系即可求出BE的长,用AB的长减去BE的长度即可.
随堂练习
三角函数的计算
用计算器求一个锐角三角函数的值
已知锐角的三角函数值求锐角
课堂小结
1、教材“习题1.4”中第1、2、3、5题
2、完成练习册中本课时的练习
作业布置
