河北省沧衡八校联盟2023-2024学年高三上学期11月期中考试数学试题(含解析)
文档属性
| 名称 | 河北省沧衡八校联盟2023-2024学年高三上学期11月期中考试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 749.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 14:01:54 | ||
图片预览




文档简介
沧衡八校联盟2023-2024学年高三上学期11月期中考试
数 学
注意事项:
1.答题前,考生务必将自己的姓名,考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:集合与常用逻辑用语,不等式,函数,导数,三角函数,平面向量,复数,数列。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,,则
A. B. C. D.
2.命题“,”的否定为
A., B.,
C., D.,
3.已知,则
A. B.5 C.3 D.
4.已知非零向量,满足,且,则与的夹角为
A. B. C. D.
5.推动小流域综合治理提质增效,推进生态清洁小流域建设是助力乡村振兴和建设美丽中国的重要途径之一.某乡村落实该举措后因地制宜,发展旅游业,预计2023年平均每户将增加4000元收入,以后每年度平均每户较上一年增长的收入是在前一年每户增长收入的基础上以10%的增速增长的,则该乡村每年度平均每户较上一年增加的收入开始超过12000元的年份大约是(参考数据:,,)
A.2033年 B.2034年 C.2035年 D.2036年
6.已知,,,则
A. B. C. D.
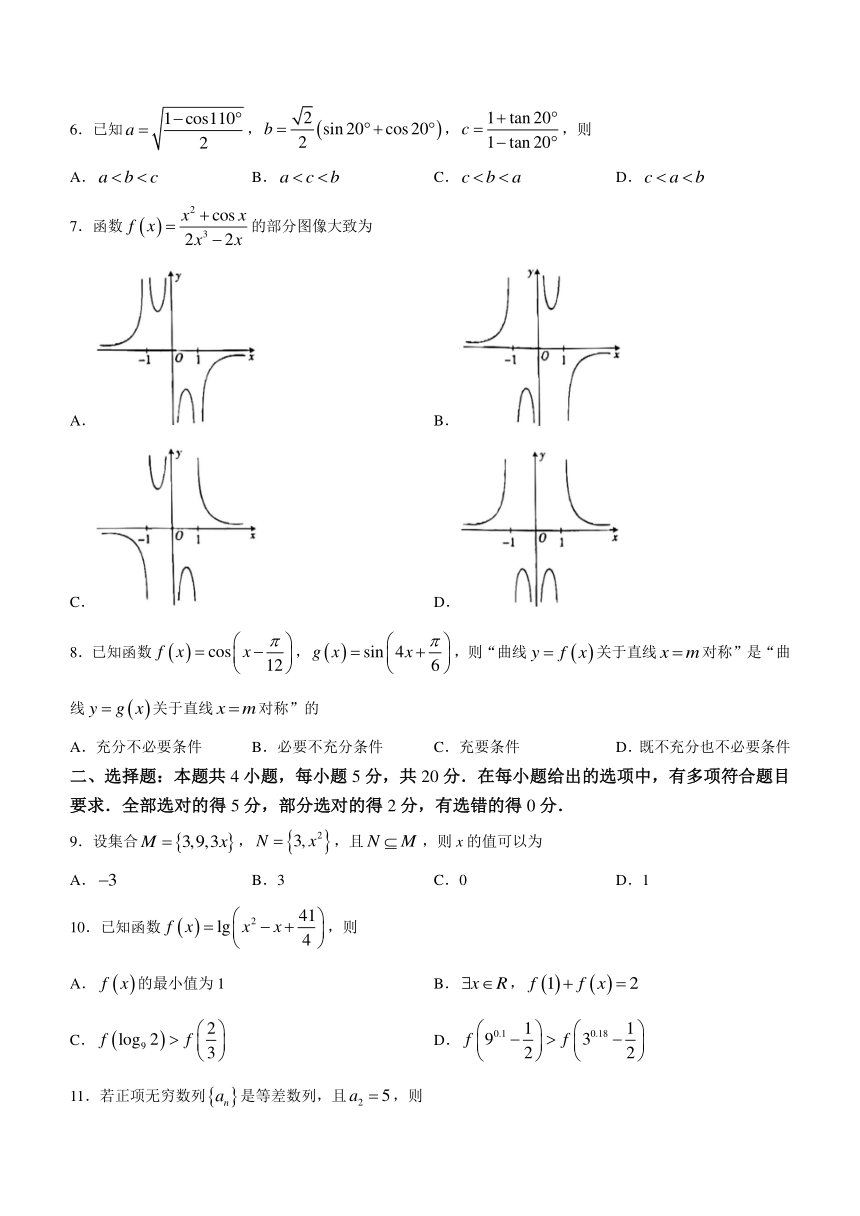
7.函数的部分图像大致为
A. B.
C. D.
8.已知函数,,则“曲线关于直线对称”是“曲线关于直线对称”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.设集合,,且,则x的值可以为
A. B.3 C.0 D.1
10.已知函数,则
A.的最小值为1 B.,
C. D.
11.若正项无穷数列是等差数列,且,则
A.当时, B.的取值范围是
C.当为整数时,的最大值为29 D.公差d的取值范围是
12.若方程有两个根,(),则
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.设△ABC内角A,B,C的对边分别是a,b,c,若,,,则 .
14.幻方是一种中国传统游戏,在我国古代的《洛书》中有记载.幻方是一种将数字安排在正方形格子中,使每行、每列和对角线上的数字之和都相等的游戏.如图,将1,2,3,…,9填入的方格内,使三行、三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数1,2,3,…,n填入个方格中,使得每行、每列和两条对角线上的数字之和都相等,则这个正方形叫做n阶幻方.记n阶幻方的每行数字之和为,例如,则 .
15.已知函数对于任意x,,总有,当时,,且,则不等式的解集为 .
16.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.为了纪念数学家高斯,我们把取整函数,称为高斯函数,其中表示不超过x的最大整数,例如,.已知等差数列满足,,,则 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
在△ABC中,角A,B,C的对边分别为a,b,c.已知,,.
(1)求c的值;
(2)求的值;
(3)求的值.
18.(12分)
已知函数(,,)的部分图象如图所示.
(1)求的解析式;
(2)设函数,求的单调递增区间.
19.(12分)
已知函数在处取得极值.
(1)求a的值;
(2)求在上的值域.
20.(12分)
为了减少碳排放,某企业采用新工艺,将生产中产生的二氧化碳转化为一种化工产品.已知该企业每月的处理量最少为30吨,最多为400吨.月处理成本(元)与月处理量x(吨)之间的函数关系近似地表示为.
(1)当该企业每月的处理量为多少吨时,才能使月处理成本最低?月处理成本最低是多少元?
(2)当该企业每月的处理量为多少吨时,才能使每吨的平均处理成本最低?每吨的平均处理成本最低是多少元?
21.(12分)
已知为单调递增的等差数列,为等比数列,,的前n项和为.
(1)求,的通项公式;
(2)设的前n项和为,若(),记,求.
22.(12分)
已知函数,.
(1)求的单调区间;
(2)证明:.
沧衡八校联盟2023-2024学年高三上学期11月期中考试
数学参考答案
1.D
因为,,所以.
2.D
因为全称量词命题的否定是存在量词命题,所以选D.
3.B
因为,所以.
4.A
因为,所以.设与的夹角为,则,解得.
5.C
设经过n年之后,每年度平均每户收入增加y元,由题得,即,则,.又,则.所以所求年份大约是2035年.
6.A
因为,,,又,所以.
7.C
函数的定义域为,因为,所以为奇函数,排除D.因为,所以当时,,当时,,排除A,B,故选C.
8.A
令(),得(),所以曲线关于直线()对称.令(),得(),所以曲线关于直线()对称.因为真包含于,所以“曲线关于直线对称”是“曲线关于直线对称”的充分不必要条件.
9.AC
因为,所以或,解得或.当时,,集合M中的元素不满足互异性,故舍去.当时,符合题意.当时,也符合题意.所以选A,C.
10.ACD
,A正确.
因为当且仅当时,取得最小值,且最小值为1,所以,所以,B错误.
因为,所以,又,且在上单调递减,在上单调递增,所以,C正确.
因为,所以,所以,D正确.
11.ABC
当时,公差,,A正确.因为是正项等差数列,所以,且,所以公差d的取值范围是,D错误.因为,所以的取值范围是,B正确.,当为整数时,的最大值为29,C正确.
12.BCD
易得函数在上单调递增,且过点.函数的简图如图所示.
由题意可得,,,即
因为,所以,A错误.
令函数,.当时,,当时,,所以在上单调递增,在上单调递减,所以,即,当且仅当时,等号成立.
结合②可得,即,B正确.
结合①可得,即,所以,C正确.
因为,,所以.
①-②得,即,D正确.
13.
因为,,所以,由,得,解得.
14.260
在n阶幻方中填入数字1,2,3,…,,共n行,这个数字之和为,由于这n行数字之和都相等,所以每一行数字之和,故.
15.
由题意可知,令,得,则为奇函数.设,则,因为当时,,所以,则,所以在R上单调递增.由,得,所以.可化为,所以,解得.
16.8
根据题意得,即,所以,
所以.
17.解:
(1)因为,所以.
因为,所以,解得.
(2)由(1)可得.
因为,所以,解得.
(3),
,
.
.
18.解:
(1)易知,
由图知,则,,.
当时,(),解得().
因为,所以,则.
(2)因为,
要求其单调递增区间,只要(),
解得(),
所以的单调递增区间为().
19.解:
(1).
因为在处取得极值,所以,解得.
经检验,符合题意.
(2)由(1)可得.
当时,,当时,,
所以在上单调递增,在上单调递减,
.
又,,
所以在上的值域为.
20.解:
(1)该企业的月处理成,
因为,在上单调递减,在上单调递增,
所以当该企业每月的处理量为300吨时,才能使月处理成本最低,月处理成本最低是19800元.
(2)因为(),
所以每吨的平均处理成本.
因为,当且仅当时,等号成立,
所以,
当该企业每月的处理量为360吨时,每吨的平均处理成本最低,最低为60元.
21.解:
(1)当时,,
又,所以.
当时,.
设的公差为d,的公比为q,则,,
即,
解得或(舍去),
所以,.
(2)因为的前n项和,
所以.
又因为(,),
所以数列(,)是首项为,公比为的等比数列,
所以.
22.
(1)解:的定义域为,.
令,得,此时函数单调递增;
令,得,此时函数单调递减.
所以的单调递减区间为,单调递增区间为.
(2)证明:令(),则.
当时,.
当时,令,则,
因为,,所以,即单调递减.
又,,
所以存在,使.
所以当时,,函数单调递增,
当时,,函数单调递减,
所以.
因为,所以,即,
所以.
因为,,且在上单调递减,
所以,同时,
所以.
因为,所以,
又因为,所以,即.
数 学
注意事项:
1.答题前,考生务必将自己的姓名,考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:集合与常用逻辑用语,不等式,函数,导数,三角函数,平面向量,复数,数列。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,,则
A. B. C. D.
2.命题“,”的否定为
A., B.,
C., D.,
3.已知,则
A. B.5 C.3 D.
4.已知非零向量,满足,且,则与的夹角为
A. B. C. D.
5.推动小流域综合治理提质增效,推进生态清洁小流域建设是助力乡村振兴和建设美丽中国的重要途径之一.某乡村落实该举措后因地制宜,发展旅游业,预计2023年平均每户将增加4000元收入,以后每年度平均每户较上一年增长的收入是在前一年每户增长收入的基础上以10%的增速增长的,则该乡村每年度平均每户较上一年增加的收入开始超过12000元的年份大约是(参考数据:,,)
A.2033年 B.2034年 C.2035年 D.2036年
6.已知,,,则
A. B. C. D.
7.函数的部分图像大致为
A. B.
C. D.
8.已知函数,,则“曲线关于直线对称”是“曲线关于直线对称”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.设集合,,且,则x的值可以为
A. B.3 C.0 D.1
10.已知函数,则
A.的最小值为1 B.,
C. D.
11.若正项无穷数列是等差数列,且,则
A.当时, B.的取值范围是
C.当为整数时,的最大值为29 D.公差d的取值范围是
12.若方程有两个根,(),则
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.设△ABC内角A,B,C的对边分别是a,b,c,若,,,则 .
14.幻方是一种中国传统游戏,在我国古代的《洛书》中有记载.幻方是一种将数字安排在正方形格子中,使每行、每列和对角线上的数字之和都相等的游戏.如图,将1,2,3,…,9填入的方格内,使三行、三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数1,2,3,…,n填入个方格中,使得每行、每列和两条对角线上的数字之和都相等,则这个正方形叫做n阶幻方.记n阶幻方的每行数字之和为,例如,则 .
15.已知函数对于任意x,,总有,当时,,且,则不等式的解集为 .
16.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号.为了纪念数学家高斯,我们把取整函数,称为高斯函数,其中表示不超过x的最大整数,例如,.已知等差数列满足,,,则 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
在△ABC中,角A,B,C的对边分别为a,b,c.已知,,.
(1)求c的值;
(2)求的值;
(3)求的值.
18.(12分)
已知函数(,,)的部分图象如图所示.
(1)求的解析式;
(2)设函数,求的单调递增区间.
19.(12分)
已知函数在处取得极值.
(1)求a的值;
(2)求在上的值域.
20.(12分)
为了减少碳排放,某企业采用新工艺,将生产中产生的二氧化碳转化为一种化工产品.已知该企业每月的处理量最少为30吨,最多为400吨.月处理成本(元)与月处理量x(吨)之间的函数关系近似地表示为.
(1)当该企业每月的处理量为多少吨时,才能使月处理成本最低?月处理成本最低是多少元?
(2)当该企业每月的处理量为多少吨时,才能使每吨的平均处理成本最低?每吨的平均处理成本最低是多少元?
21.(12分)
已知为单调递增的等差数列,为等比数列,,的前n项和为.
(1)求,的通项公式;
(2)设的前n项和为,若(),记,求.
22.(12分)
已知函数,.
(1)求的单调区间;
(2)证明:.
沧衡八校联盟2023-2024学年高三上学期11月期中考试
数学参考答案
1.D
因为,,所以.
2.D
因为全称量词命题的否定是存在量词命题,所以选D.
3.B
因为,所以.
4.A
因为,所以.设与的夹角为,则,解得.
5.C
设经过n年之后,每年度平均每户收入增加y元,由题得,即,则,.又,则.所以所求年份大约是2035年.
6.A
因为,,,又,所以.
7.C
函数的定义域为,因为,所以为奇函数,排除D.因为,所以当时,,当时,,排除A,B,故选C.
8.A
令(),得(),所以曲线关于直线()对称.令(),得(),所以曲线关于直线()对称.因为真包含于,所以“曲线关于直线对称”是“曲线关于直线对称”的充分不必要条件.
9.AC
因为,所以或,解得或.当时,,集合M中的元素不满足互异性,故舍去.当时,符合题意.当时,也符合题意.所以选A,C.
10.ACD
,A正确.
因为当且仅当时,取得最小值,且最小值为1,所以,所以,B错误.
因为,所以,又,且在上单调递减,在上单调递增,所以,C正确.
因为,所以,所以,D正确.
11.ABC
当时,公差,,A正确.因为是正项等差数列,所以,且,所以公差d的取值范围是,D错误.因为,所以的取值范围是,B正确.,当为整数时,的最大值为29,C正确.
12.BCD
易得函数在上单调递增,且过点.函数的简图如图所示.
由题意可得,,,即
因为,所以,A错误.
令函数,.当时,,当时,,所以在上单调递增,在上单调递减,所以,即,当且仅当时,等号成立.
结合②可得,即,B正确.
结合①可得,即,所以,C正确.
因为,,所以.
①-②得,即,D正确.
13.
因为,,所以,由,得,解得.
14.260
在n阶幻方中填入数字1,2,3,…,,共n行,这个数字之和为,由于这n行数字之和都相等,所以每一行数字之和,故.
15.
由题意可知,令,得,则为奇函数.设,则,因为当时,,所以,则,所以在R上单调递增.由,得,所以.可化为,所以,解得.
16.8
根据题意得,即,所以,
所以.
17.解:
(1)因为,所以.
因为,所以,解得.
(2)由(1)可得.
因为,所以,解得.
(3),
,
.
.
18.解:
(1)易知,
由图知,则,,.
当时,(),解得().
因为,所以,则.
(2)因为,
要求其单调递增区间,只要(),
解得(),
所以的单调递增区间为().
19.解:
(1).
因为在处取得极值,所以,解得.
经检验,符合题意.
(2)由(1)可得.
当时,,当时,,
所以在上单调递增,在上单调递减,
.
又,,
所以在上的值域为.
20.解:
(1)该企业的月处理成,
因为,在上单调递减,在上单调递增,
所以当该企业每月的处理量为300吨时,才能使月处理成本最低,月处理成本最低是19800元.
(2)因为(),
所以每吨的平均处理成本.
因为,当且仅当时,等号成立,
所以,
当该企业每月的处理量为360吨时,每吨的平均处理成本最低,最低为60元.
21.解:
(1)当时,,
又,所以.
当时,.
设的公差为d,的公比为q,则,,
即,
解得或(舍去),
所以,.
(2)因为的前n项和,
所以.
又因为(,),
所以数列(,)是首项为,公比为的等比数列,
所以.
22.
(1)解:的定义域为,.
令,得,此时函数单调递增;
令,得,此时函数单调递减.
所以的单调递减区间为,单调递增区间为.
(2)证明:令(),则.
当时,.
当时,令,则,
因为,,所以,即单调递减.
又,,
所以存在,使.
所以当时,,函数单调递增,
当时,,函数单调递减,
所以.
因为,所以,即,
所以.
因为,,且在上单调递减,
所以,同时,
所以.
因为,所以,
又因为,所以,即.
同课章节目录
