周期现象,角的推广(北师大版)
图片预览








文档简介
课件25张PPT。高中数学·必修4·北师大版第一章 三角函数
§1 周期现象
§2 角的概念的推广 [学习目标]
1.通过实际情境,感知周期现象,能判断简单的实际问题中的周期.
2.理解正角、负角、零角与象限角的概念.
3.掌握终边相同角的表示方法. [知识链接]
1.用精简的文字语言概括出周期现象的关键特征是什么?
答 间隔相同,重复出现.
2.手表慢了5分钟,如何校准?手表快了1.5小时,又如何校准?
答 可将分针顺时针方向旋转30°;可将时针逆时针方向旋转45°.3.在初中角是如何定义的?
答 定义1:有公共端点的两条射线组成的几何图形叫作角.
定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫作角. [预习导引]
1.周期现象
若某一现象按照 ,那么这种现象就称为周期现象.
2.角的概念
(1)角的概念:角可以看成平面内 绕着 从一个位置 到另一个位置所形成的图形.一定的规律周而复始地重复出现一条射线端点旋转(2)角的表示方法:①常用大写字母A、B、C等表示;②也可以用希腊字母α、β、γ等表示;③特别是当角作为变量时,常用字母x表示.
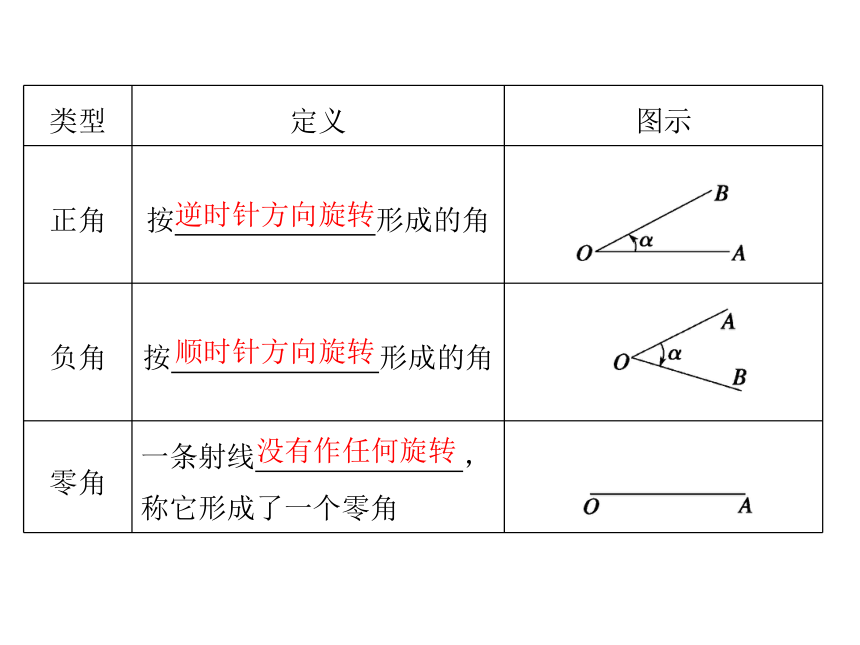
(3)角的分类:按旋转方向可将角分为如下三类:逆时针方向旋转顺时针方向旋转没有作任何旋转3.象限角
角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合,那么,角的终边(除端点外)在第几象限,就说这个角是 .如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.第几象限角4.终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与 的和.整数个周角要点一 周期现象的判定
例1 下面是一个古希腊的哲学家、数学家、天文学家毕达哥拉斯的故事:有一次毕达哥拉斯处罚学生,让他来回数在黛安娜神庙的七根柱子(这七根柱子的标号分别为A,B,C,…,G),如图所示,一直到指出第1 999个数的柱子的标号是哪一个才能够停止.你能帮助这名学生尽快结束这个处罚吗?A B C D E F G
1 2 3 4 5 6 7
13 12 11 10 9 8
14 15 16 17 18 19
25 24 23 22 21 20
… … … … … …
… … … … … …解 通过观察可发现规律:数“2,3,4,…,1 997,1 998,1 999”按标号为“B,C,D,E,F,G,F,E,D,C,B,A”这12个字母循环出现,因此周期是12.先把1去掉,(1 999-1)÷12=166……6,因此第1 999个数的柱子的标号与第167个周期的第6个数的标号相同,故数到第1 999个数的柱子的标号是G.
规律方法 对周期现象的判断,首先要认真审题,明确题目的实际背景,然后应牢牢抓住“间隔相同,现象(或值)重复出现”这一重要特征进行判断.跟踪演练1 2014年5月1日是星期四,问2014年10月1日是星期几?
解 按照公历记法,2014年5、7、8这三个月份都是31天,6、9月份各30天.从2014年5月1日到2014年10月1日共有153天,因为每星期有7天,故由153=22×7-1知,从2014年5月1日再过154天恰好与5月1日相同都是星期四,这一天是公历2014年10月2日,故2014年10月1日是星期三.要点二 任意角概念的辨析
例2 在下列说法中:
①0°~90°的角是第一象限角;
②第二象限角大于第一象限角;
③钝角都是第二象限角;
④小于90°的角都是锐角.
其中错误说法的序号为________.
答案 ①②④解析 ①0°角不属于任何象限,所以①不正确.
②120°是第二象限角,390°是第一象限角,显然390°>120°,所以②不正确.
③钝角α的范围是90°<α<180°,显然是第二象限角,所以③正确.
④锐角α的范围是0°<α<90°,小于90°的角也可以是零角或负角,所以④不正确.规律方法 判断说法错误,只需举一个反例即可.解决本题关键在于正确理解各种角的定义.随着角的概念的推广,对角的认识不能再停留在初中阶段,否则判断容易错误.跟踪演练2 A={小于90°的角},B={第一象限角},则A∩B= ( )
A.{锐角} B.{小于90°的角}
C.{第一象限角} D.以上都不对
答案 D
解析 小于90°的角由锐角、零角、负角组成,而第一象限的角包含有锐角及其他终边在第一象限的角,所以A∩B是由锐角和终边在第一象限的负角组成的集合,故选D.要点三 象限角的判定
例3 在0°~360°范围内,找出与下列各角终边相同的角,并判定它们是第几象限角.
(1)-150°;(2)650°;(3)-950°15′.
解 (1)因为-150°=-360°+210°,所以在0°~360°范围内,与-150°角终边相同的角是210°角,它是第三象限角.(2)因为650°=360°+290°,所以在0°~360°范围内,
与650°角终边相同的角是290°角,它是第四象限角.
(3)因为-950°15′=-3×360°+129°45′,所以在
0°~360°范围内,与-950°15′角终边相同的角是
129°45′角,它是第二象限角.
规律方法 本题要求在0°~360°范围内,找出与已知角终
边相同的角,并判断其为第几象限角,这是为以后证明恒等
式、化简及利用诱导公式求三角函数的值打基础.跟踪演练3 给出下列四个命题:①-75°角是第四象限角;②225°角是第三象限角;③475°角是第二象限角;
④-315°是第一象限角,其中真命题有
( )
A.1个 B.2个 C.3个 D.4个
答案 D解析 对于①:如图1所示,-75°角是第四象限角;
对于②:如图2所示,225°角是第三象限角;
对于③:如图3所示,475°角是第二象限角;
对于④:如图4所示,-315°角是第一象限角.要点四 终边相同的角的应用
例4 在与角10 030°终边相同的角中,求满足下列条件的角.
(1)最大的负角;(2)最小的正角;(3)360°~720°的角.
解 (1)与10 030°终边相同的角的一般形式为β=k·360°+10 030°(k∈Z),由-360°(3)由360°≤k·360°+10 030°<720°,得-9 670°≤k·360°<-9 310°,解得k=-26,故所求的角为
β=670°.
规律方法 求适合某种条件且与已知角终边相同的角,其方法是先求出与已知角终边相同的角的一般形式,再依条件构建不等式求出k的值.跟踪演练4 写出与α=-1 910°终边相同的角的集合,并把集合中适合不等式-720°≤β<360°的元素β写出来.再见
§1 周期现象
§2 角的概念的推广 [学习目标]
1.通过实际情境,感知周期现象,能判断简单的实际问题中的周期.
2.理解正角、负角、零角与象限角的概念.
3.掌握终边相同角的表示方法. [知识链接]
1.用精简的文字语言概括出周期现象的关键特征是什么?
答 间隔相同,重复出现.
2.手表慢了5分钟,如何校准?手表快了1.5小时,又如何校准?
答 可将分针顺时针方向旋转30°;可将时针逆时针方向旋转45°.3.在初中角是如何定义的?
答 定义1:有公共端点的两条射线组成的几何图形叫作角.
定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫作角. [预习导引]
1.周期现象
若某一现象按照 ,那么这种现象就称为周期现象.
2.角的概念
(1)角的概念:角可以看成平面内 绕着 从一个位置 到另一个位置所形成的图形.一定的规律周而复始地重复出现一条射线端点旋转(2)角的表示方法:①常用大写字母A、B、C等表示;②也可以用希腊字母α、β、γ等表示;③特别是当角作为变量时,常用字母x表示.
(3)角的分类:按旋转方向可将角分为如下三类:逆时针方向旋转顺时针方向旋转没有作任何旋转3.象限角
角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合,那么,角的终边(除端点外)在第几象限,就说这个角是 .如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.第几象限角4.终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与 的和.整数个周角要点一 周期现象的判定
例1 下面是一个古希腊的哲学家、数学家、天文学家毕达哥拉斯的故事:有一次毕达哥拉斯处罚学生,让他来回数在黛安娜神庙的七根柱子(这七根柱子的标号分别为A,B,C,…,G),如图所示,一直到指出第1 999个数的柱子的标号是哪一个才能够停止.你能帮助这名学生尽快结束这个处罚吗?A B C D E F G
1 2 3 4 5 6 7
13 12 11 10 9 8
14 15 16 17 18 19
25 24 23 22 21 20
… … … … … …
… … … … … …解 通过观察可发现规律:数“2,3,4,…,1 997,1 998,1 999”按标号为“B,C,D,E,F,G,F,E,D,C,B,A”这12个字母循环出现,因此周期是12.先把1去掉,(1 999-1)÷12=166……6,因此第1 999个数的柱子的标号与第167个周期的第6个数的标号相同,故数到第1 999个数的柱子的标号是G.
规律方法 对周期现象的判断,首先要认真审题,明确题目的实际背景,然后应牢牢抓住“间隔相同,现象(或值)重复出现”这一重要特征进行判断.跟踪演练1 2014年5月1日是星期四,问2014年10月1日是星期几?
解 按照公历记法,2014年5、7、8这三个月份都是31天,6、9月份各30天.从2014年5月1日到2014年10月1日共有153天,因为每星期有7天,故由153=22×7-1知,从2014年5月1日再过154天恰好与5月1日相同都是星期四,这一天是公历2014年10月2日,故2014年10月1日是星期三.要点二 任意角概念的辨析
例2 在下列说法中:
①0°~90°的角是第一象限角;
②第二象限角大于第一象限角;
③钝角都是第二象限角;
④小于90°的角都是锐角.
其中错误说法的序号为________.
答案 ①②④解析 ①0°角不属于任何象限,所以①不正确.
②120°是第二象限角,390°是第一象限角,显然390°>120°,所以②不正确.
③钝角α的范围是90°<α<180°,显然是第二象限角,所以③正确.
④锐角α的范围是0°<α<90°,小于90°的角也可以是零角或负角,所以④不正确.规律方法 判断说法错误,只需举一个反例即可.解决本题关键在于正确理解各种角的定义.随着角的概念的推广,对角的认识不能再停留在初中阶段,否则判断容易错误.跟踪演练2 A={小于90°的角},B={第一象限角},则A∩B= ( )
A.{锐角} B.{小于90°的角}
C.{第一象限角} D.以上都不对
答案 D
解析 小于90°的角由锐角、零角、负角组成,而第一象限的角包含有锐角及其他终边在第一象限的角,所以A∩B是由锐角和终边在第一象限的负角组成的集合,故选D.要点三 象限角的判定
例3 在0°~360°范围内,找出与下列各角终边相同的角,并判定它们是第几象限角.
(1)-150°;(2)650°;(3)-950°15′.
解 (1)因为-150°=-360°+210°,所以在0°~360°范围内,与-150°角终边相同的角是210°角,它是第三象限角.(2)因为650°=360°+290°,所以在0°~360°范围内,
与650°角终边相同的角是290°角,它是第四象限角.
(3)因为-950°15′=-3×360°+129°45′,所以在
0°~360°范围内,与-950°15′角终边相同的角是
129°45′角,它是第二象限角.
规律方法 本题要求在0°~360°范围内,找出与已知角终
边相同的角,并判断其为第几象限角,这是为以后证明恒等
式、化简及利用诱导公式求三角函数的值打基础.跟踪演练3 给出下列四个命题:①-75°角是第四象限角;②225°角是第三象限角;③475°角是第二象限角;
④-315°是第一象限角,其中真命题有
( )
A.1个 B.2个 C.3个 D.4个
答案 D解析 对于①:如图1所示,-75°角是第四象限角;
对于②:如图2所示,225°角是第三象限角;
对于③:如图3所示,475°角是第二象限角;
对于④:如图4所示,-315°角是第一象限角.要点四 终边相同的角的应用
例4 在与角10 030°终边相同的角中,求满足下列条件的角.
(1)最大的负角;(2)最小的正角;(3)360°~720°的角.
解 (1)与10 030°终边相同的角的一般形式为β=k·360°+10 030°(k∈Z),由-360°
β=670°.
规律方法 求适合某种条件且与已知角终边相同的角,其方法是先求出与已知角终边相同的角的一般形式,再依条件构建不等式求出k的值.跟踪演练4 写出与α=-1 910°终边相同的角的集合,并把集合中适合不等式-720°≤β<360°的元素β写出来.再见
