第一单元 第11课时 《表面涂色的正方体》教学课件(共33张PPT)六年级数学上册苏教版
文档属性
| 名称 | 第一单元 第11课时 《表面涂色的正方体》教学课件(共33张PPT)六年级数学上册苏教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 18:06:10 | ||
图片预览









文档简介
(共33张PPT)
第11课时 表面涂色的正方体 小学数学 · 六年级(上) ·SJ
使学生通过自主探究,发现表面涂色大正方 体切成若干个相同小正方体后,小正方体不 同涂色面个数的规律。
通过观察、归纳得出每种涂色情况的小正方
体的位置与数量的关系,经历从特殊到一般的 过程。
使学生进一步感受图形学习的乐趣,获得成功 的体验,提高数学学习的兴趣,增强学习数学的 信心。
01.
学习目标
L e a n i n g o bj e ctiv e s
1
3
2
通过活动中找、数、算等数学操作,感受“ 归纳” 这一数学思想。
探究并发现表面涂色大正方体切成若干个相 同小正方体后,小正方体不同涂色面个数的 规律。
理解大正方体的棱平均分的份数、切成小正方体的 总个数和不同涂色面的小正方体个数之间的关系。
学习重点
学习难点
核心素养
02.
重点难点
L e a n i n g p o i n t s
课前导入
L e a d i n
正方体有6个面,每个面都是相同的 正方形, 8个顶点, 12条棱,每条棱 都相等。
正方体有什么特征?
知识链接
k n o w l e d g e li n k
如果棱长用n表示 ,小正方 体的个数就是n3。
小正方体的个数就是棱 长的立方。
快速说出下面每个正方体是由多少个小正体构成的。
知识链接
k n o w l e d g e li n k
8 27
125
64
学习任务一
实践活动:数一数
。 探究新知
p r e s e n t a t i o n
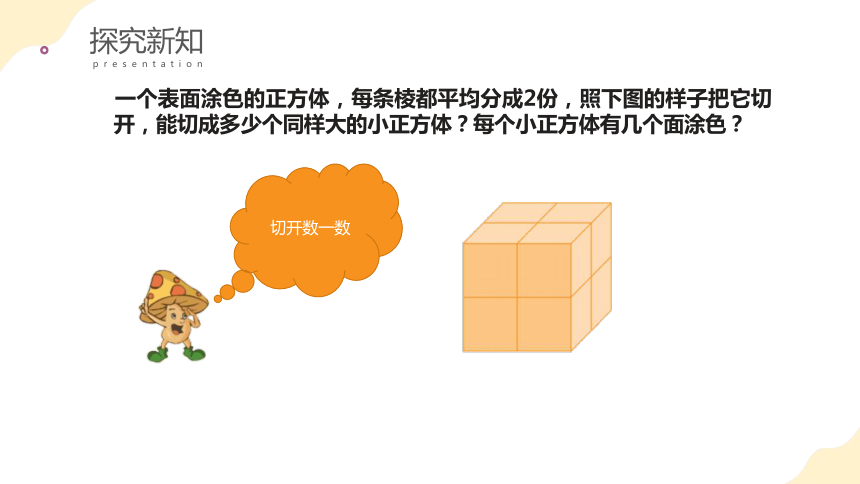
一个表面涂色的正方体,每条棱都平均分成2份,照下图的样子把它切
切开数一数
开,能切成多少个同样大的小正方体?每个小正方体有几个面涂色?
2×2×2=8 (个),能切 成8个小正方体。
每个小正方体都有3 个面涂色。
。 探究新知
p r e s e n t a t i o n
探究新知
p r e s e n t a t i o n
如果像下图这样把正方体切开,能切成多少个小正方体?切成的小正方 体中, 3面涂色、 2面涂色、 1面涂色的各有多少个,分别在什么位置?
你有哪些方法来数?
可以分类
数
可以一面 一面数
还可以......
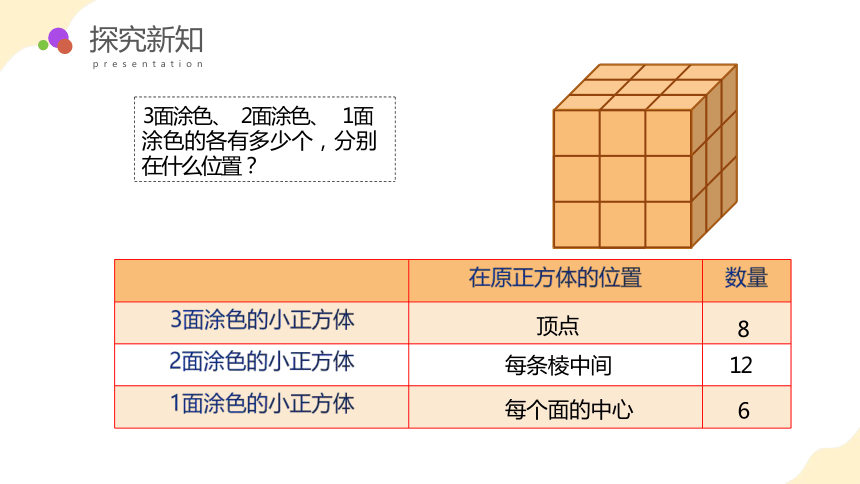
顶点
8
每条棱中间
12
每个面的中心
6
3面涂色、 2面涂色、 1面 涂色的各有多少个,分别 在什么位置?
探究新知
p r e s e n t a t i o n
如果把这个正方体的每条棱平均分成4份, 5份切成的小正方体中, 3 面涂色、 2面涂色、 1面涂色的各有多少个,分别在什么位置?
先仔细观察, 想一想,
再数一数。
。 探究新知
p r e s e n t a t i o n
2面涂色的小正方 体有24个,在棱的 中间。
1面涂色的小正方 体有24个,在每个 面的中心。
3面涂色的小正 方体有8个,都在 顶点处。
探究新知
p r e s e n t a t i o n
数 一 数
2面涂色的小正方 体有36个,在棱的 中间。
1面涂色的小正方 体有54个,在每个 面的中心。
3面涂色的小正 方体有8个,都在 顶点处。
探究新知
p r e s e n t a t i o n
大正方体的棱 平均分的份数 3 4
5
切成小正方体 的总个数
3面涂色的小 正方体个数 8 8
8
2面涂色的小 正方体个数 12 24
36
1面涂色的小 正方体个数 6 24
54
探究新知
p r e s e n t a t i o n
把一个正方体沿着每条棱平均分成3份、 4份、 5份切成小正方体, 最后 结果如下:
学习任务二
寻找规律
探究新知
p r e s e n t a t i o n
如果把这个正方体的每条棱平均分成6份, 7份......切成的小正方体中,
试着数一数 ,想一想 ,还 有什么办法吗?
3面涂色、 2面涂色、 1面涂色的各有多少个?
④ ⑤ ⑥ ⑦
⑧
三面涂色的个数 8 8 8 8
8
两面涂色的个数 36 48 60 72
84
一面涂色的个数 54 96 150 216
294
没有涂色的个数 8 27 64 125
216
你还能继续来分吗? 在数的过程中你会 遇到什么问题?
这会不会有一定的规律呢?
探究新知
p r e s e n t a t i o n
填 一 填
不管分成多少个正方体 ,三面涂色的正方 体始终是顶点处的8个。
这和正方体的顶 点数一致。
三面涂色的正方体个数
探究新知
p r e s e n t a t i o n
三面涂色的都是8个
两面涂色的正方体个数
24个
分成3份时 ,每条棱上1个 , 分成4份时 ,每条棱上3个 , 分成5份时 ,每条棱上3个。
......
两面涂色的正方体数量就是用每条棱 分成的份数减2再乘12。
每条棱上的个数是分成的 份数减2
它们都在每条棱上 ,所 以都是12的倍数。
。 探究新知
p r e s e n t a t i o n
36个
12个
每个面上有(棱长分成 的份数-2) 的平方个
都在每个面的中心
探究新知
p r e s e n t a t i o n
一面涂色的正方体个数
6个
54个
24个
。 探究新知
p r e s e n t a t i o n
根据上面的探索,填写下表
n
8
12(n-2)
6(n-2)
125
8
36
54
27
8
12
6
64
8
24
24
8
8
0
0
n
探究新知
p r e s e n t a t i o n
如果用n表示把大正方体的棱平均分的份数,用a、b分别表示2面涂 色和1面涂色的小正方体个数,你能用式子分别表示n和a、b的关系 吗
a = 12(n-2) , b= 6 n-2)2
找各种小正方体时,要注 意它们在大正方体上的位 置。 各种小正方体的个数与 正方体顶点、面和棱的 个(条)数有关。
回顾探索和发现规律的过程, 说说你的体会。
要把找、 数、 算等方 法结合起来, 并根据 图形的特征进行思考。
探究新知
p r e s e n t a t i o n
学习任务三
达标检测,巩固练习
。 达标练习
p r a c t i c e
1.选择题
(1)用相同的小正方形搭稍大的正方体,最少要( C )块。 A.4
B. 6 C. 8 D. 16
(2)小娟用棱长1厘米的小正方体木块拼成一个棱长5厘米的大正方体,并
把这个大正方体的表面涂成红色,其中一面涂色的小正方体有( D)个。
A. 8 B. 12 C. 36 D. 54
。 达标练习
p r a c t i c e
2.一个棱长是4cm的正方体,表面涂满红色,如果把它切成棱长是
1cm的小正方体,那么其中三面涂有红色的小正方体有( 8 )个,
没有面涂红色的小正方体有( 8 )个。
因为切成棱长是1cm的小正方体,所以每条棱上有4个小正方体, 所以没有面涂红色的小正方体有:
(4-1-1) ×(4-1-1) ×(4-1-1)= 2×2×2=8个
三面有红色的小立方体只能在8个顶点上,所以三面涂色的小正方 体有8个。
。 达标练习
p r a c t i c e
3.判断题
(1)把一个表面涂满色的正方体棱长二等分,三面涂色的小正方体有8
个。( √ )
(2)用棱长是1厘米的小正方体拼成棱长是5厘米的大正方体后,再把
它们的表面分别涂上颜色, 一面涂色的小正方体有54块。( √ )
(3)一个表面涂色的正方体,先把棱平均分成5份,再切成同样大的小
正方体,两面涂色的小正方体有24个。( × )
(4)把一个表面涂满色的正方体棱长五等分,三面涂色的小正方体有8
个,两面涂色的有36个。( √ )
● 达标练习
p r a c t i c e
4.小明将一个表面涂色的正方体木块的棱长平均分成若干份,并锯成同样大
的小正方体。他想要48个两面涂色的小正方体,需要把棱长平均分成几份
48÷12=4 4+2=6(份)
答:需要把棱长平均分成6份。
。 达标练习
p r a c t i c e
5.( 2021秋 ·江苏 ·六年级期中) 下图是一个表面被涂上橙色的棱长为10 厘米的正方体木块,如果把它沿虚线切成8个正方体,这些小正方体中没 有被涂上颜色的所有表面的面积和是多少平方厘米?
5×5×6×8 =
25×6×8=1200 (平
方厘米)
1200-600=600 (平方厘米)
10×10×6=100×6 = 600 (平方厘米)
10÷2=5 (厘米)
答:这些小正方体中没有被涂上红色的所有表面的面积和是600平方厘米。
。 达标练习
p r a c t i c e
6.( 2022秋.江苏连云港.竞赛) 在一个正方体木块的6个面上涂上红色
后,把它分割成若干个棱长是1 cm的小正方体木块,两面涂红色的 小正方体木块共有108个,那么只有一面涂红色的小正方体木块有多
6×( 11-2)2
=6×92
=6×81
=486 (个)
108÷12+2
=9+2
=11
答:只有一面涂红色的小正方体木块有486个。
少个?
各种小正方体的个数与正方体的顶点、面和棱的个(条)数有关。
2面涂色的小正方体的个数是12(n-2); 3面涂色的小正方体的个 数是6(n-2)2。
这节课你有什么收获?
找各种小正方体时,要注意它们在大正方体上的位置。
知识总结
s u m m a r y
2
1
3
同学们再见
THANKS FOR WATCHING
第11课时 表面涂色的正方体 小学数学 · 六年级(上) ·SJ
使学生通过自主探究,发现表面涂色大正方 体切成若干个相同小正方体后,小正方体不 同涂色面个数的规律。
通过观察、归纳得出每种涂色情况的小正方
体的位置与数量的关系,经历从特殊到一般的 过程。
使学生进一步感受图形学习的乐趣,获得成功 的体验,提高数学学习的兴趣,增强学习数学的 信心。
01.
学习目标
L e a n i n g o bj e ctiv e s
1
3
2
通过活动中找、数、算等数学操作,感受“ 归纳” 这一数学思想。
探究并发现表面涂色大正方体切成若干个相 同小正方体后,小正方体不同涂色面个数的 规律。
理解大正方体的棱平均分的份数、切成小正方体的 总个数和不同涂色面的小正方体个数之间的关系。
学习重点
学习难点
核心素养
02.
重点难点
L e a n i n g p o i n t s
课前导入
L e a d i n
正方体有6个面,每个面都是相同的 正方形, 8个顶点, 12条棱,每条棱 都相等。
正方体有什么特征?
知识链接
k n o w l e d g e li n k
如果棱长用n表示 ,小正方 体的个数就是n3。
小正方体的个数就是棱 长的立方。
快速说出下面每个正方体是由多少个小正体构成的。
知识链接
k n o w l e d g e li n k
8 27
125
64
学习任务一
实践活动:数一数
。 探究新知
p r e s e n t a t i o n
一个表面涂色的正方体,每条棱都平均分成2份,照下图的样子把它切
切开数一数
开,能切成多少个同样大的小正方体?每个小正方体有几个面涂色?
2×2×2=8 (个),能切 成8个小正方体。
每个小正方体都有3 个面涂色。
。 探究新知
p r e s e n t a t i o n
探究新知
p r e s e n t a t i o n
如果像下图这样把正方体切开,能切成多少个小正方体?切成的小正方 体中, 3面涂色、 2面涂色、 1面涂色的各有多少个,分别在什么位置?
你有哪些方法来数?
可以分类
数
可以一面 一面数
还可以......
顶点
8
每条棱中间
12
每个面的中心
6
3面涂色、 2面涂色、 1面 涂色的各有多少个,分别 在什么位置?
探究新知
p r e s e n t a t i o n
如果把这个正方体的每条棱平均分成4份, 5份切成的小正方体中, 3 面涂色、 2面涂色、 1面涂色的各有多少个,分别在什么位置?
先仔细观察, 想一想,
再数一数。
。 探究新知
p r e s e n t a t i o n
2面涂色的小正方 体有24个,在棱的 中间。
1面涂色的小正方 体有24个,在每个 面的中心。
3面涂色的小正 方体有8个,都在 顶点处。
探究新知
p r e s e n t a t i o n
数 一 数
2面涂色的小正方 体有36个,在棱的 中间。
1面涂色的小正方 体有54个,在每个 面的中心。
3面涂色的小正 方体有8个,都在 顶点处。
探究新知
p r e s e n t a t i o n
大正方体的棱 平均分的份数 3 4
5
切成小正方体 的总个数
3面涂色的小 正方体个数 8 8
8
2面涂色的小 正方体个数 12 24
36
1面涂色的小 正方体个数 6 24
54
探究新知
p r e s e n t a t i o n
把一个正方体沿着每条棱平均分成3份、 4份、 5份切成小正方体, 最后 结果如下:
学习任务二
寻找规律
探究新知
p r e s e n t a t i o n
如果把这个正方体的每条棱平均分成6份, 7份......切成的小正方体中,
试着数一数 ,想一想 ,还 有什么办法吗?
3面涂色、 2面涂色、 1面涂色的各有多少个?
④ ⑤ ⑥ ⑦
⑧
三面涂色的个数 8 8 8 8
8
两面涂色的个数 36 48 60 72
84
一面涂色的个数 54 96 150 216
294
没有涂色的个数 8 27 64 125
216
你还能继续来分吗? 在数的过程中你会 遇到什么问题?
这会不会有一定的规律呢?
探究新知
p r e s e n t a t i o n
填 一 填
不管分成多少个正方体 ,三面涂色的正方 体始终是顶点处的8个。
这和正方体的顶 点数一致。
三面涂色的正方体个数
探究新知
p r e s e n t a t i o n
三面涂色的都是8个
两面涂色的正方体个数
24个
分成3份时 ,每条棱上1个 , 分成4份时 ,每条棱上3个 , 分成5份时 ,每条棱上3个。
......
两面涂色的正方体数量就是用每条棱 分成的份数减2再乘12。
每条棱上的个数是分成的 份数减2
它们都在每条棱上 ,所 以都是12的倍数。
。 探究新知
p r e s e n t a t i o n
36个
12个
每个面上有(棱长分成 的份数-2) 的平方个
都在每个面的中心
探究新知
p r e s e n t a t i o n
一面涂色的正方体个数
6个
54个
24个
。 探究新知
p r e s e n t a t i o n
根据上面的探索,填写下表
n
8
12(n-2)
6(n-2)
125
8
36
54
27
8
12
6
64
8
24
24
8
8
0
0
n
探究新知
p r e s e n t a t i o n
如果用n表示把大正方体的棱平均分的份数,用a、b分别表示2面涂 色和1面涂色的小正方体个数,你能用式子分别表示n和a、b的关系 吗
a = 12(n-2) , b= 6 n-2)2
找各种小正方体时,要注 意它们在大正方体上的位 置。 各种小正方体的个数与 正方体顶点、面和棱的 个(条)数有关。
回顾探索和发现规律的过程, 说说你的体会。
要把找、 数、 算等方 法结合起来, 并根据 图形的特征进行思考。
探究新知
p r e s e n t a t i o n
学习任务三
达标检测,巩固练习
。 达标练习
p r a c t i c e
1.选择题
(1)用相同的小正方形搭稍大的正方体,最少要( C )块。 A.4
B. 6 C. 8 D. 16
(2)小娟用棱长1厘米的小正方体木块拼成一个棱长5厘米的大正方体,并
把这个大正方体的表面涂成红色,其中一面涂色的小正方体有( D)个。
A. 8 B. 12 C. 36 D. 54
。 达标练习
p r a c t i c e
2.一个棱长是4cm的正方体,表面涂满红色,如果把它切成棱长是
1cm的小正方体,那么其中三面涂有红色的小正方体有( 8 )个,
没有面涂红色的小正方体有( 8 )个。
因为切成棱长是1cm的小正方体,所以每条棱上有4个小正方体, 所以没有面涂红色的小正方体有:
(4-1-1) ×(4-1-1) ×(4-1-1)= 2×2×2=8个
三面有红色的小立方体只能在8个顶点上,所以三面涂色的小正方 体有8个。
。 达标练习
p r a c t i c e
3.判断题
(1)把一个表面涂满色的正方体棱长二等分,三面涂色的小正方体有8
个。( √ )
(2)用棱长是1厘米的小正方体拼成棱长是5厘米的大正方体后,再把
它们的表面分别涂上颜色, 一面涂色的小正方体有54块。( √ )
(3)一个表面涂色的正方体,先把棱平均分成5份,再切成同样大的小
正方体,两面涂色的小正方体有24个。( × )
(4)把一个表面涂满色的正方体棱长五等分,三面涂色的小正方体有8
个,两面涂色的有36个。( √ )
● 达标练习
p r a c t i c e
4.小明将一个表面涂色的正方体木块的棱长平均分成若干份,并锯成同样大
的小正方体。他想要48个两面涂色的小正方体,需要把棱长平均分成几份
48÷12=4 4+2=6(份)
答:需要把棱长平均分成6份。
。 达标练习
p r a c t i c e
5.( 2021秋 ·江苏 ·六年级期中) 下图是一个表面被涂上橙色的棱长为10 厘米的正方体木块,如果把它沿虚线切成8个正方体,这些小正方体中没 有被涂上颜色的所有表面的面积和是多少平方厘米?
5×5×6×8 =
25×6×8=1200 (平
方厘米)
1200-600=600 (平方厘米)
10×10×6=100×6 = 600 (平方厘米)
10÷2=5 (厘米)
答:这些小正方体中没有被涂上红色的所有表面的面积和是600平方厘米。
。 达标练习
p r a c t i c e
6.( 2022秋.江苏连云港.竞赛) 在一个正方体木块的6个面上涂上红色
后,把它分割成若干个棱长是1 cm的小正方体木块,两面涂红色的 小正方体木块共有108个,那么只有一面涂红色的小正方体木块有多
6×( 11-2)2
=6×92
=6×81
=486 (个)
108÷12+2
=9+2
=11
答:只有一面涂红色的小正方体木块有486个。
少个?
各种小正方体的个数与正方体的顶点、面和棱的个(条)数有关。
2面涂色的小正方体的个数是12(n-2); 3面涂色的小正方体的个 数是6(n-2)2。
这节课你有什么收获?
找各种小正方体时,要注意它们在大正方体上的位置。
知识总结
s u m m a r y
2
1
3
同学们再见
THANKS FOR WATCHING
