数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-19 20:57:47 | ||
图片预览




文档简介
(共15张PPT)
202X
单击添加副标题
2.5.1 直线与圆的位置关系
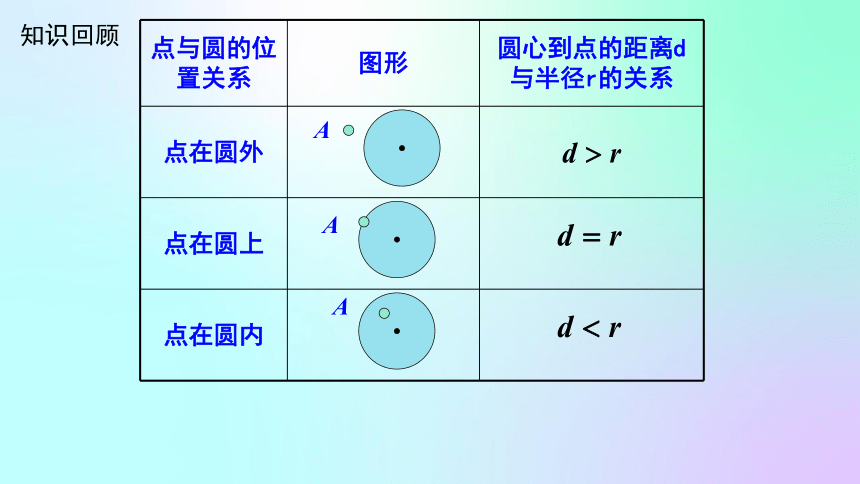
知识回顾
点与圆的位置关系 图形 圆心到点的距离d与半径r的关系
点在圆外
点在圆上
点在圆内
学习目标
1.掌握直线与圆的三种位置关系:相交、相切、相离.(重点)
2.会用代数法和几何法来判断直线与圆的三种位置关系.(难点)
3.会用直线与圆的位置关系解决一些实际问题.(难点)
课程标准
能根据给定直线、圆的方程,判断直线与圆的位置关系.
海上生明月
将月亮看作成一个圆,海天交线看作一条直线,通过月出的过程,你能感受到直线与圆的位置关系吗?
情境导入
自主学习 阅读课本P91-92
1.在平面中,直线与圆的位置关系有几种?交点情况?
2.如何利用几何法判断直线与圆的位置关系?
3.类比两直线的位置关系的研究方法,如何通过代数方法,研究直线与圆的位置关系?
4.根据例1总结求直线与圆相交的弦长的方法?
5.你还有其他方法求例1的弦长吗?
6.由判断直线与圆的位置关系和求弦长的方法你有什么感想?
合作学习
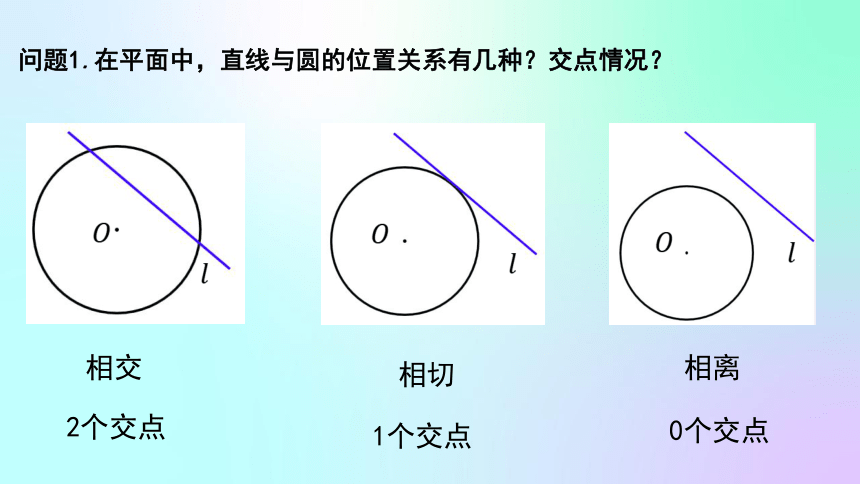
问题1.在平面中,直线与圆的位置关系有几种?交点情况?
相交
相切
相离
2个交点
1个交点
0个交点
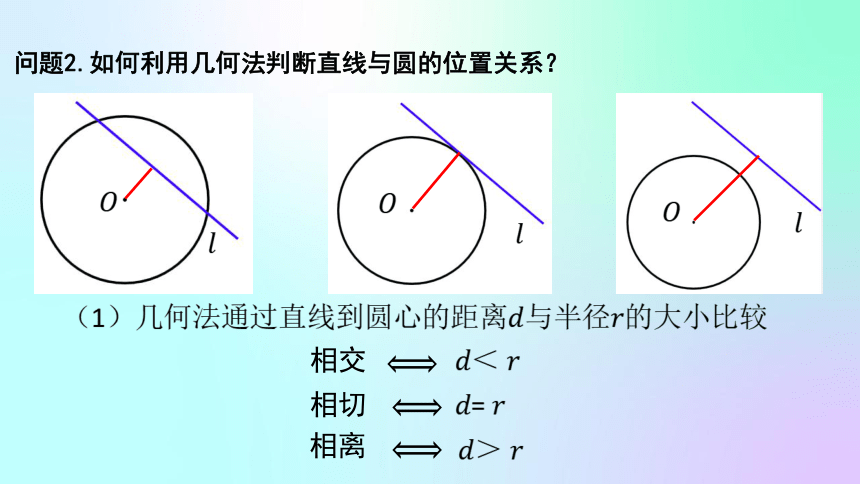
问题2.如何利用几何法判断直线与圆的位置关系?
相交
相切
相离
问题3.类比两直线的位置关系的研究方法,如何通过代数方法,研究直线与圆的位置关系?
(2)代数法:
① △>0
消去x(或y),得到关于x(或y)的一元二次方程,
利用判别式△确定解的情况,
直线l与圆C相交;
方程有两不等实根
② △=0
直线l与圆C相切;
方程有两个相等实根
③ △<0
直线l与圆C相离.
方程无实数根
直线l:Ax+By+C=0
圆C:x2+ y2+Dx+Ey+F=0(D2+E2-4F>0)
判断直线与圆位置关系:
追问:利用几何法、代数法都可以判断直线与圆的位置关系,哪种方法简单?
1:判断下列各组直线l与圆C的位置关系。
(1)直线l:x-y+1=0; 圆C:x2+y2=3;
(2)直线l:3x+4y+2=0;圆C:x2+y2-2x=0;
(3)直线l:x+y+3=0; 圆C:x2+y2+2y=0;
典例分析
例1 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
弦长问题
解法1(几何法):
过圆心C点作CD垂直AB,由勾股定理可得 ;
也就是垂径定理;可以求得
解法2(代数法):
解二元一次方程 ;解得 ;
带入直线的方程中,得到两个交点坐标为A(2,0),B(1,3);
求两点间的距离:
点拨
弦长公式
练习3.
判断直线2x-y+2=0与圆(x-1)2+(y-2)2=4的位置关系;如果相交,求直线被圆截得的弦长。
直线与圆的位置关系 相交 相切 相离
图示
直线与圆的交点个数 2个 1个 0个
几何法:圆心到直线的距离
代数法:联立直线与圆的方程,消元得px2+qx+t=0的解的个数(△的正负)
小结
课堂小结
2.弦长问题
当堂检测(5分钟)
1.直线3x+4y+12=0与圆(x-1)2+(y-1)2=9的位置关系是( )
A.相交并且直线过圆心 B.相交但不过圆心
C.相切 D.相离
作业:课本P98 习题2.5 1,3
202X
单击添加副标题
2.5.1 直线与圆的位置关系
知识回顾
点与圆的位置关系 图形 圆心到点的距离d与半径r的关系
点在圆外
点在圆上
点在圆内
学习目标
1.掌握直线与圆的三种位置关系:相交、相切、相离.(重点)
2.会用代数法和几何法来判断直线与圆的三种位置关系.(难点)
3.会用直线与圆的位置关系解决一些实际问题.(难点)
课程标准
能根据给定直线、圆的方程,判断直线与圆的位置关系.
海上生明月
将月亮看作成一个圆,海天交线看作一条直线,通过月出的过程,你能感受到直线与圆的位置关系吗?
情境导入
自主学习 阅读课本P91-92
1.在平面中,直线与圆的位置关系有几种?交点情况?
2.如何利用几何法判断直线与圆的位置关系?
3.类比两直线的位置关系的研究方法,如何通过代数方法,研究直线与圆的位置关系?
4.根据例1总结求直线与圆相交的弦长的方法?
5.你还有其他方法求例1的弦长吗?
6.由判断直线与圆的位置关系和求弦长的方法你有什么感想?
合作学习
问题1.在平面中,直线与圆的位置关系有几种?交点情况?
相交
相切
相离
2个交点
1个交点
0个交点
问题2.如何利用几何法判断直线与圆的位置关系?
相交
相切
相离
问题3.类比两直线的位置关系的研究方法,如何通过代数方法,研究直线与圆的位置关系?
(2)代数法:
① △>0
消去x(或y),得到关于x(或y)的一元二次方程,
利用判别式△确定解的情况,
直线l与圆C相交;
方程有两不等实根
② △=0
直线l与圆C相切;
方程有两个相等实根
③ △<0
直线l与圆C相离.
方程无实数根
直线l:Ax+By+C=0
圆C:x2+ y2+Dx+Ey+F=0(D2+E2-4F>0)
判断直线与圆位置关系:
追问:利用几何法、代数法都可以判断直线与圆的位置关系,哪种方法简单?
1:判断下列各组直线l与圆C的位置关系。
(1)直线l:x-y+1=0; 圆C:x2+y2=3;
(2)直线l:3x+4y+2=0;圆C:x2+y2-2x=0;
(3)直线l:x+y+3=0; 圆C:x2+y2+2y=0;
典例分析
例1 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆C的位置关系;如果相交,求直线l被圆C所截得的弦长.
弦长问题
解法1(几何法):
过圆心C点作CD垂直AB,由勾股定理可得 ;
也就是垂径定理;可以求得
解法2(代数法):
解二元一次方程 ;解得 ;
带入直线的方程中,得到两个交点坐标为A(2,0),B(1,3);
求两点间的距离:
点拨
弦长公式
练习3.
判断直线2x-y+2=0与圆(x-1)2+(y-2)2=4的位置关系;如果相交,求直线被圆截得的弦长。
直线与圆的位置关系 相交 相切 相离
图示
直线与圆的交点个数 2个 1个 0个
几何法:圆心到直线的距离
代数法:联立直线与圆的方程,消元得px2+qx+t=0的解的个数(△的正负)
小结
课堂小结
2.弦长问题
当堂检测(5分钟)
1.直线3x+4y+12=0与圆(x-1)2+(y-1)2=9的位置关系是( )
A.相交并且直线过圆心 B.相交但不过圆心
C.相切 D.相离
作业:课本P98 习题2.5 1,3
