2014-2015学年高中数学(北师大版)必修四课件:第一章 第9节 三角函数的简单应用
文档属性
| 名称 | 2014-2015学年高中数学(北师大版)必修四课件:第一章 第9节 三角函数的简单应用 |  | |
| 格式 | zip | ||
| 文件大小 | 266.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-06 21:23:11 | ||
图片预览








文档简介
课件26张PPT。高中数学·必修4·北师大版§9 三角函数的简单应用[学习目标]
1.会用三角函数解决一些简单的实际问题.
2.体会三角函数是描述周期变化现象的重要函数模型.[知识链接]
1.数学模型是什么?建立数学模型的方法是什么?
答 简单地说,数学模型就是把实际问题用数学语言抽象概括,再从数学角度来反映或近似地反映实际问题时,所得出的关于实际问题的数学描述.数学模型的方法,是把实际问题加以抽象概括,建立相应的数学模型,利用这些模型来研究实际问题的一般数学方法.2.上述的数学模型建立的一般程序是什么?
答 解决问题的一般程序是:
1°审题:逐字逐句的阅读题意,审清楚题目条件、要求、理解数学关系;
2°建模:分析题目变化趋势,选择适当函数模型;
3°求解:对所建立的数学模型进行分析研究得到数学结论;
4°还原:把数学结论还原为实际问题的解答.A+k -A+k 3.三角函数模型的应用
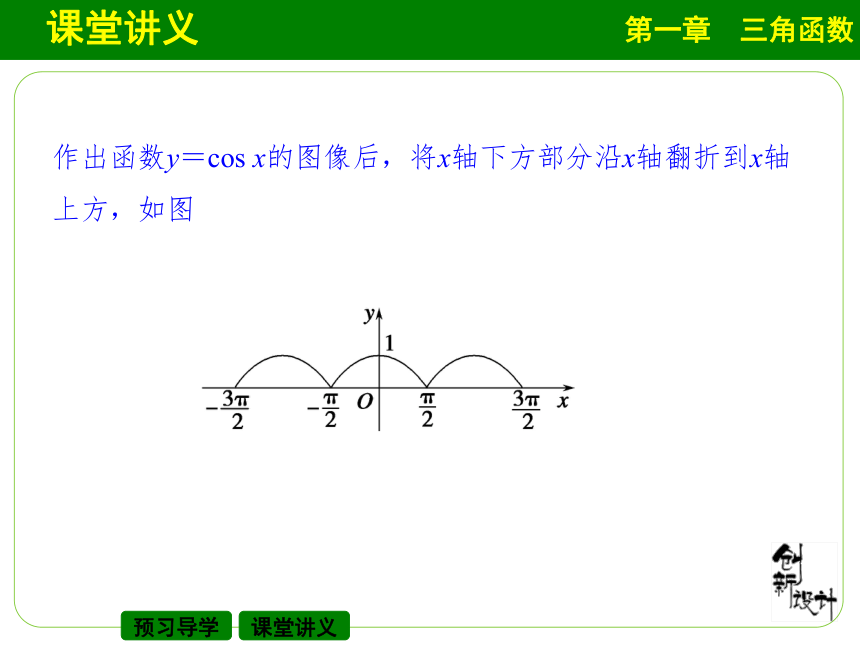
三角函数作为描述现实世界中 现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.周期作出函数y=cos x的图像后,将x轴下方部分沿x轴翻折到x轴上方,如图规律方法 翻折法作函数图像
(1)要得到y=|f(x)|的图像,只需将y=f(x)的图像在x轴下方的部分沿x轴翻折到上方,即“下翻上”.
(2)要得到y=f(|x|)的图像,只需将y=f(x)的图像在y轴右边的部分沿y轴翻折到左边,即“右翻左”,同时保留右边的部分.要点二 应用函数模型解题
例2 已知电流I与时间t的关系为I=Asin(ωt+φ).规律方法 例题中的函数模型已经给出,观察图像和利用待定系数法可以求出解析式中的未知参数,从而确定函数解析式.此类问题解题关键是将图形语言转化为符号语言,其中,读图、识图、用图是数形结合的有效途径.要点三 构建函数模型解题
例3 如图,游乐场中的摩天轮匀速转动,
每转一圈需要12分钟,其中圆心O距离
地面40.5米,半径为40米.如果你从最
低处登上摩天轮,那么你与地面的距离
将随时间的变化而变化,以你登上摩天
轮的时刻开始计时,请解答下列问题:
(1)求出你与地面的距离y(米)与时间t(分钟)的函数关系式;
(2)当你第4次距离地面60.5米时,用了多长时间?规律方法 建立三角函数模型解决实际问题时,首先寻找与角有关的信息,确定选用正弦、余弦还是正切型函数模型;其次是搜集数据,建立三角函数解析式并解题;最后将所得结果翻译成实际答案,要注意根据实际作答.跟踪演练3 以一年为一个周期调查某商品出厂价格及该商品在商店的销售价格时发现:该商品的出厂价格是在6元基础上按月份随正弦型函数y1波动的,已知3月份出厂价格最高为8元,7月份出厂价格最低为4元,而该商品在商店的销售价格是在8元基础上按月份随正弦型函数y2波动的,并已知5月份销售价格最高为10元,9月份销售价格最低为6元,假设某商店每月购进这种商品m件,且当月售完,请分别求出y1、y2关于第x月份的函数解析式.再见
1.会用三角函数解决一些简单的实际问题.
2.体会三角函数是描述周期变化现象的重要函数模型.[知识链接]
1.数学模型是什么?建立数学模型的方法是什么?
答 简单地说,数学模型就是把实际问题用数学语言抽象概括,再从数学角度来反映或近似地反映实际问题时,所得出的关于实际问题的数学描述.数学模型的方法,是把实际问题加以抽象概括,建立相应的数学模型,利用这些模型来研究实际问题的一般数学方法.2.上述的数学模型建立的一般程序是什么?
答 解决问题的一般程序是:
1°审题:逐字逐句的阅读题意,审清楚题目条件、要求、理解数学关系;
2°建模:分析题目变化趋势,选择适当函数模型;
3°求解:对所建立的数学模型进行分析研究得到数学结论;
4°还原:把数学结论还原为实际问题的解答.A+k -A+k 3.三角函数模型的应用
三角函数作为描述现实世界中 现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.周期作出函数y=cos x的图像后,将x轴下方部分沿x轴翻折到x轴上方,如图规律方法 翻折法作函数图像
(1)要得到y=|f(x)|的图像,只需将y=f(x)的图像在x轴下方的部分沿x轴翻折到上方,即“下翻上”.
(2)要得到y=f(|x|)的图像,只需将y=f(x)的图像在y轴右边的部分沿y轴翻折到左边,即“右翻左”,同时保留右边的部分.要点二 应用函数模型解题
例2 已知电流I与时间t的关系为I=Asin(ωt+φ).规律方法 例题中的函数模型已经给出,观察图像和利用待定系数法可以求出解析式中的未知参数,从而确定函数解析式.此类问题解题关键是将图形语言转化为符号语言,其中,读图、识图、用图是数形结合的有效途径.要点三 构建函数模型解题
例3 如图,游乐场中的摩天轮匀速转动,
每转一圈需要12分钟,其中圆心O距离
地面40.5米,半径为40米.如果你从最
低处登上摩天轮,那么你与地面的距离
将随时间的变化而变化,以你登上摩天
轮的时刻开始计时,请解答下列问题:
(1)求出你与地面的距离y(米)与时间t(分钟)的函数关系式;
(2)当你第4次距离地面60.5米时,用了多长时间?规律方法 建立三角函数模型解决实际问题时,首先寻找与角有关的信息,确定选用正弦、余弦还是正切型函数模型;其次是搜集数据,建立三角函数解析式并解题;最后将所得结果翻译成实际答案,要注意根据实际作答.跟踪演练3 以一年为一个周期调查某商品出厂价格及该商品在商店的销售价格时发现:该商品的出厂价格是在6元基础上按月份随正弦型函数y1波动的,已知3月份出厂价格最高为8元,7月份出厂价格最低为4元,而该商品在商店的销售价格是在8元基础上按月份随正弦型函数y2波动的,并已知5月份销售价格最高为10元,9月份销售价格最低为6元,假设某商店每月购进这种商品m件,且当月售完,请分别求出y1、y2关于第x月份的函数解析式.再见
