2014-2015学年高中数学(北师大版)必修四课件:第一章 第7节 正切函数
文档属性
| 名称 | 2014-2015学年高中数学(北师大版)必修四课件:第一章 第7节 正切函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-06 00:00:00 | ||
图片预览









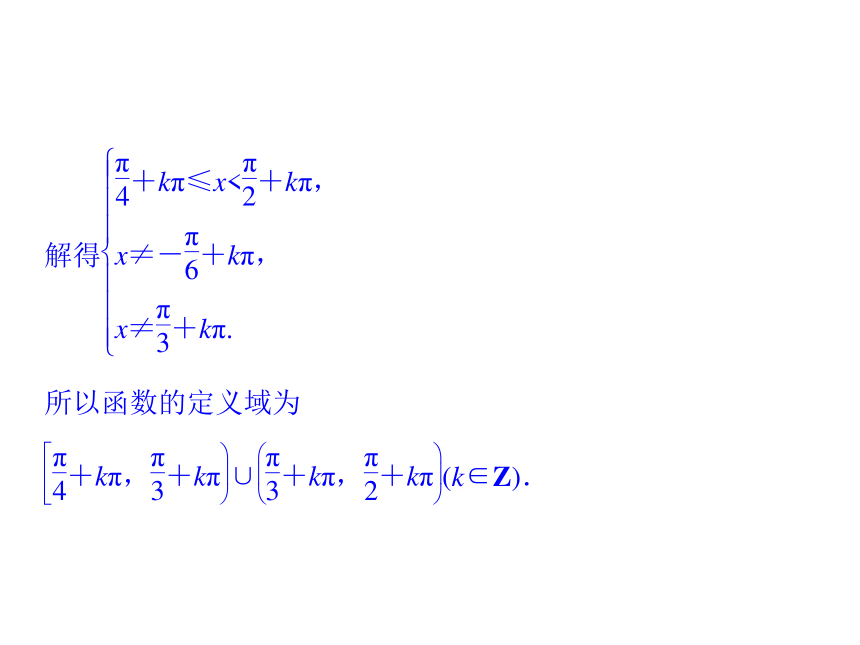

文档简介
课件31张PPT。高中数学·必修4·北师大版§7 正切函数
7.1 正切函数的定义
7.2 正切函数的图像与性质
7.3 正切函数的诱导公式[学习目标]
1.能根据正、余弦函数的定义类比得正切函数的定义.
2.了解正切函数图像的画法,能利用正切函数的图像及性质解决有关问题.
3.能根据正、余弦函数的诱导公式推出正切函数的诱导公式.3.根据相关诱导公式,你能判断正切函数是周期函数吗?其最小正周期为多少?
答 由诱导公式tan(x+π)=tan x,可知正切函数是周期函数,最小正周期是π
4.根据相关诱导公式,你能判断正切函数具有奇偶性吗?
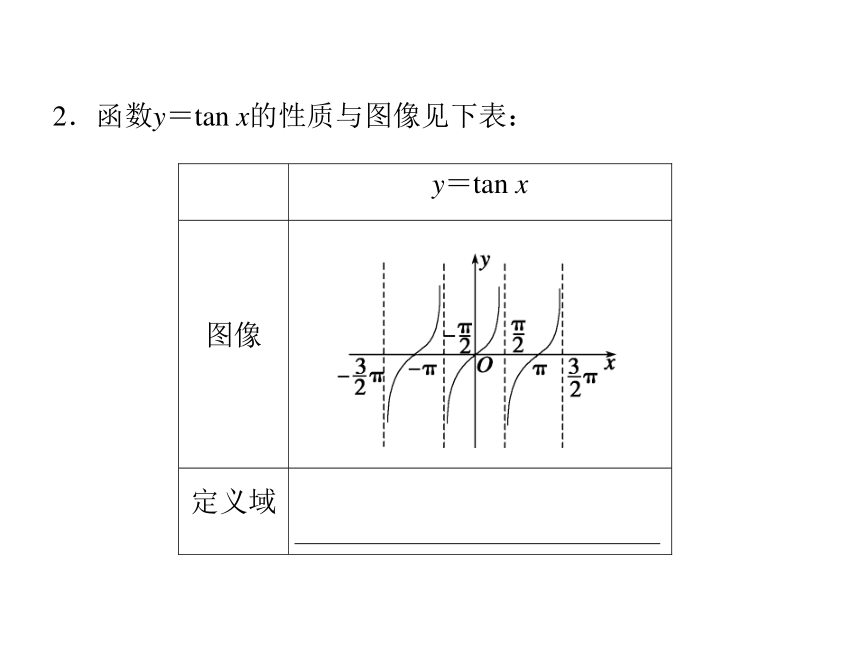
答 从正切函数的图像来看,正切曲线关于原点对称;从诱导公式来看,tan(-x)=-tan x.故正切函数是奇函数.正切函数2.函数y=tan x的性质与图像见下表:3.正切函数的诱导公式
tan(x+kπ)= (k∈Z);
tan(2π+x)= ;
tan(-x)= ;
tan(2π-x)= ;
tan(π-x)= ;
tan(π+x)= .tan xtan x-tan x-tan x-tan xtan x规律方法 求定义域时,要注意正切函数自身的限制条件,另外解不等式时要充分利用三角函数的图像或三角函数线.规律方法 正切型函数单调性求法与正、余弦型函数求法一样,采用整体代入法,但要注意区间为开区间且只有单调增区间或单调减区间.利用单调性比较大小要把角转化到同一单调区间内.规律方法 对于形如y=tan(ωx+φ)(ω、 φ为非零常数)的函数性质和图像的研究,应以正切函数的性质与图像为基础,运用整体思想和换元法求解.如果ω<0,一般先利用诱导公式将x的系数化为正数,再进行求解.规律方法 利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:(1)从一边开始,使得它等于另一边,一般由繁到简.(2)左右归一法:即证明左右两边都等于同一个式子.(3)凑合法:即针对题设与结论间的差异,有针对性地进行变形,以消除其差异,简言之,即化异为同.再见
7.1 正切函数的定义
7.2 正切函数的图像与性质
7.3 正切函数的诱导公式[学习目标]
1.能根据正、余弦函数的定义类比得正切函数的定义.
2.了解正切函数图像的画法,能利用正切函数的图像及性质解决有关问题.
3.能根据正、余弦函数的诱导公式推出正切函数的诱导公式.3.根据相关诱导公式,你能判断正切函数是周期函数吗?其最小正周期为多少?
答 由诱导公式tan(x+π)=tan x,可知正切函数是周期函数,最小正周期是π
4.根据相关诱导公式,你能判断正切函数具有奇偶性吗?
答 从正切函数的图像来看,正切曲线关于原点对称;从诱导公式来看,tan(-x)=-tan x.故正切函数是奇函数.正切函数2.函数y=tan x的性质与图像见下表:3.正切函数的诱导公式
tan(x+kπ)= (k∈Z);
tan(2π+x)= ;
tan(-x)= ;
tan(2π-x)= ;
tan(π-x)= ;
tan(π+x)= .tan xtan x-tan x-tan x-tan xtan x规律方法 求定义域时,要注意正切函数自身的限制条件,另外解不等式时要充分利用三角函数的图像或三角函数线.规律方法 正切型函数单调性求法与正、余弦型函数求法一样,采用整体代入法,但要注意区间为开区间且只有单调增区间或单调减区间.利用单调性比较大小要把角转化到同一单调区间内.规律方法 对于形如y=tan(ωx+φ)(ω、 φ为非零常数)的函数性质和图像的研究,应以正切函数的性质与图像为基础,运用整体思想和换元法求解.如果ω<0,一般先利用诱导公式将x的系数化为正数,再进行求解.规律方法 利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:(1)从一边开始,使得它等于另一边,一般由繁到简.(2)左右归一法:即证明左右两边都等于同一个式子.(3)凑合法:即针对题设与结论间的差异,有针对性地进行变形,以消除其差异,简言之,即化异为同.再见
