探索三角形全等的条件

课件15张PPT。 5.4 探索三角形全等的条件(一)授课人:闫学华教学目标1.经历探索三角形全等条件的过程,体会利用操作,归纳获得数学结论的过程.
2.掌握三角形全等的判定条件(一)---"边边边"
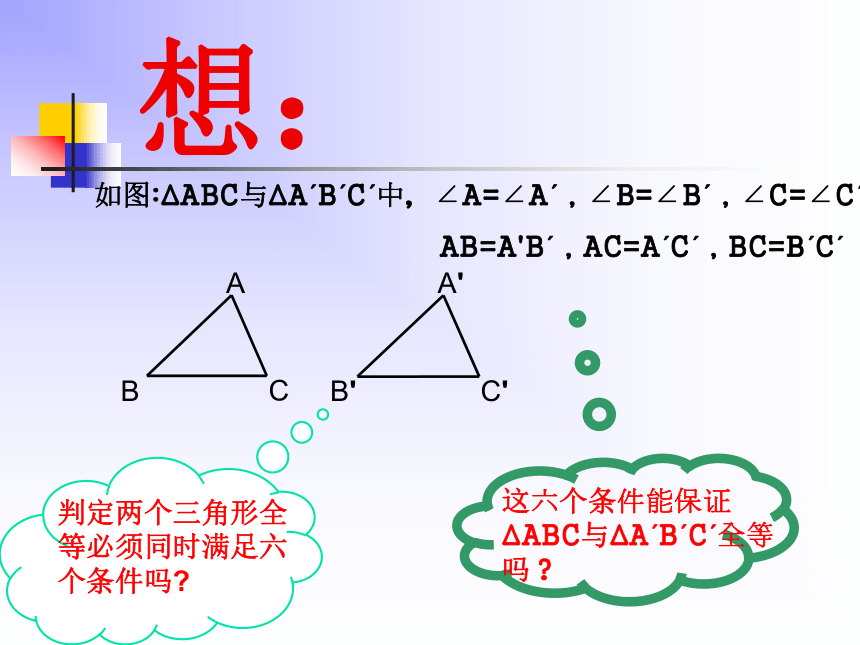
如图:ΔABC与ΔA′B′C′中，∠A=∠A′ , ∠B=∠B′ , ∠C=∠C′
AB=A'B′ , AC=A′C′ , BC=B′C′
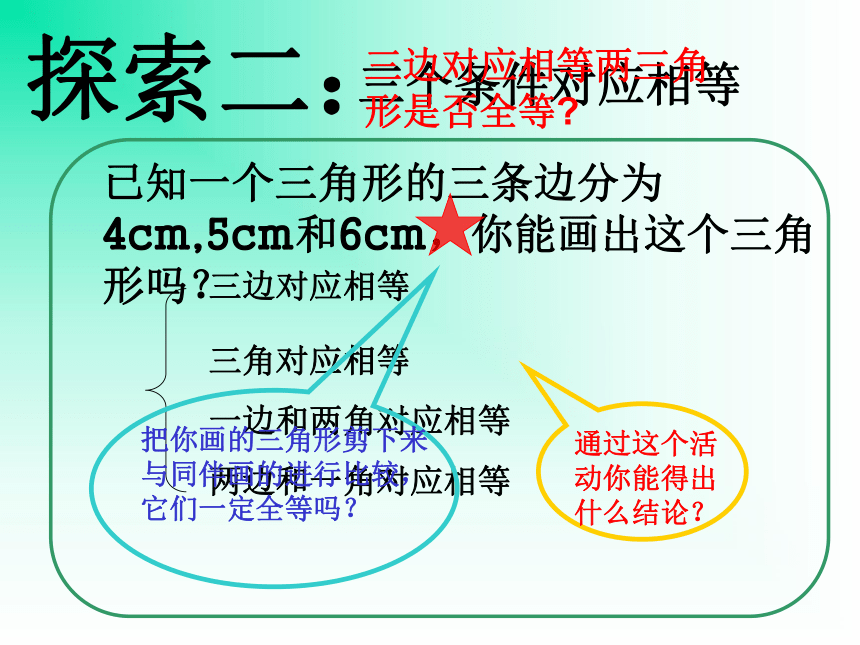
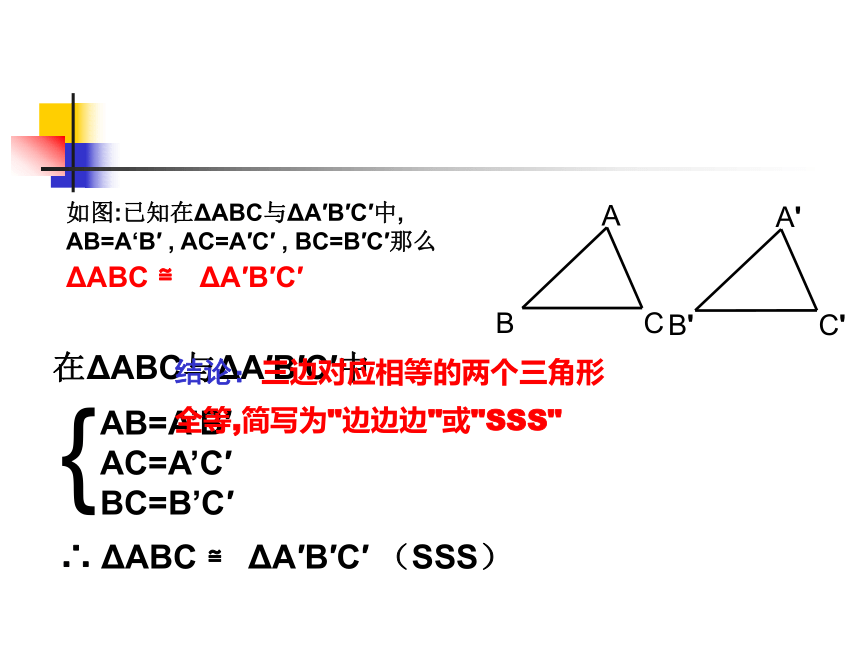
想：一个条件对应相等：两个条件对应相等：探索一:结论:通过观察,比较,探索我们知道,只给出一个或两个条件时,都不能保证两个三角形一定全等!!!探索二：三个条件对应相等三边对应相等两三角形是否全等?如图:已知在ΔABC与ΔA′B′C′中, AB=A‘B′ , AC=A′C′ , BC=B′C′那么ΔABC ≌ ΔA′B′C′
∴ ΔABC ≌ ΔA′B′C′ （SSS）
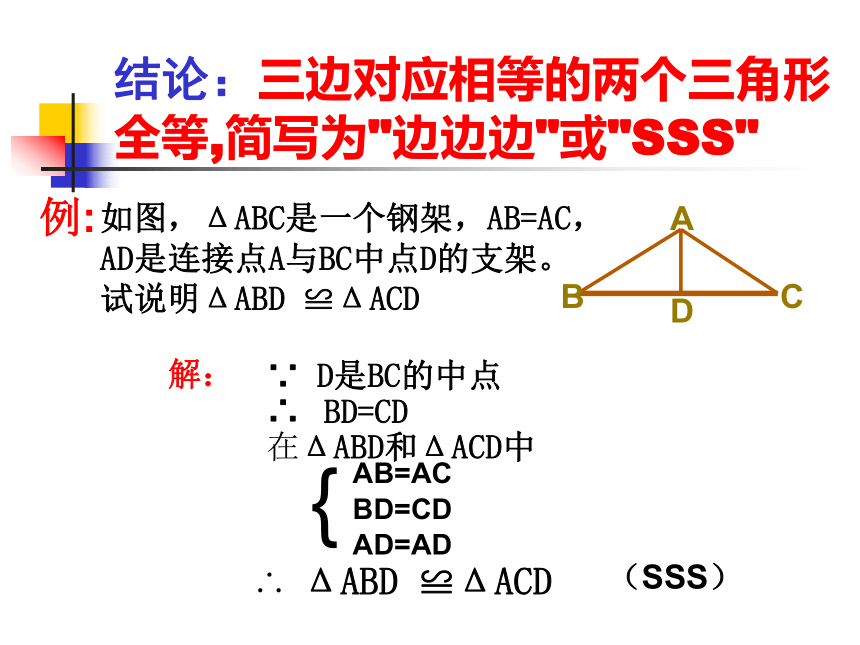
结论：三边对应相等的两个三角形全等,简写为"边边边"或"SSS" 解：D是BC的中点∵∴BD=CD在ΔABD和ΔACD中AB=ACBD=CDAD=AD{∴ ΔABD ≌ΔACD
（SSS）结论：三边对应相等的两个三角形全等,简写为"边边边"或"SSS" 例:我们一起做1.ΔACEΔACD“三月三放风筝”如图是小明制作的风筝，他根据DE=DF，EH=FH，不用度量就知道∠DEH= ∠ DFH，聪明的你请帮小明说明为什么？并写下解题过程。我们一起做2.本节课你有什么收获?1.经历了探索三角形全等条件的过程,知道了判定两个三角形全等至少需要三个条件.
2.掌握三角形全等的判定条件(一)---"边边边"
1. 96页练习题
2. 103页习题第1题，第2题作业谢谢指导还应有BC=EF∵由BE=CF可得：BE+EC=CF+EC，即BC=EF
2.一个条件对应相等：两个条件对应相等：探索一: