2.4单摆(共16张ppt)物理人教版(2019)选择性必修第一册
文档属性
| 名称 | 2.4单摆(共16张ppt)物理人教版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-20 08:50:10 | ||
图片预览






文档简介
(共16张PPT)
第二章 机械振动
第4节 单摆
温故知新
1、什么是简谐运动
2、做简谐运动物体的回复力有什么特点
知识回顾
① x-t 图像为正弦曲线
② F-x 满足 F=-kx 的形式
满足 F=-kx的形式且总是指向平衡位置
生活中经常可以看到悬挂起来的物体在竖直平面内往复运动。
摆动的钟摆、荡起的秋千、晃动的枝条它们在平衡位置附近的往复运动是不是简谐运动呢?为了解决这个问题,让我们认识一个新的模型 —— 单摆。
一. 单摆
1. 定义 : 细线一端固定在悬点,另一端系一个小球,如果细线的长度不可改变,细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
(理想化模型)
2. 模型条件 :
(1)摆球:可看成质点(体积小 质量大)
(2)摆线:① 质量远小于摆球质量
② 长度远大于小球直径
③ 不可伸缩,伸长量忽略不计。
(3)空气阻力远小于摆球的重力
注意:实际应用的单摆小球大小不可忽略,
摆长 L=摆线长度+小球半径
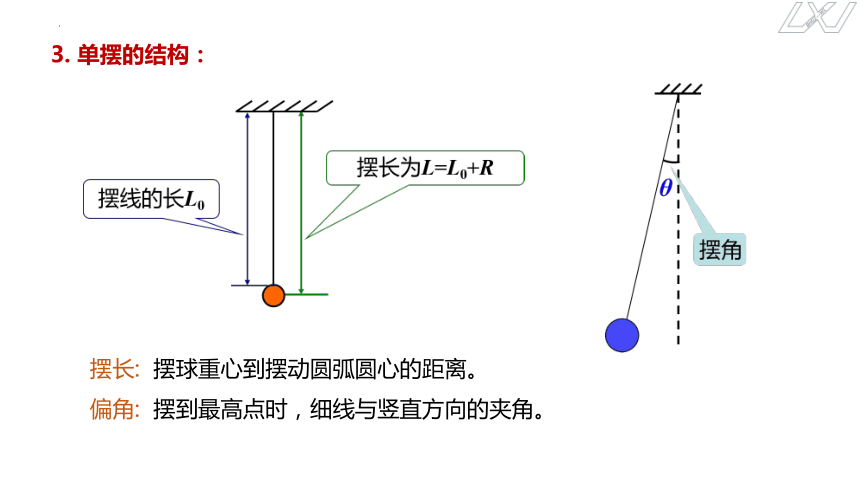
摆长: 摆球重心到摆动圆弧圆心的距离。
偏角: 摆到最高点时,细线与竖直方向的夹角。
3. 单摆的结构:
【思考与讨论】用什么方法探究单摆的振动是否为简谐运动?
1. 位移与时间的关系是否满足正弦关系(x–t 图像法)
2. 回复力与位移是否成正比且方向相反(F=-kx)
回复力来源: F G1 mgsin
角很小时(θ<5°),用弧度制表示的与它的正弦值近似相等 sin
即:F = G1 mgsin mg x (方向与位移方向相反),满足 F k x 形式。
结论:在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动。
一般偏角 F k x (k )
二. 单摆的回复力
三. 单摆的周期
单摆振动的周期与哪些因素有关呢?
1、猜想:
2、证明方法:
控制变量法
【实验1】周期与摆球的质量是否有关
【结论】单摆振动周期和摆球质量无关
【实验2】周期是否与振幅有关?
【结论】单摆的振动周期与其振幅无关(等时性)
【实验3】周期与摆球的摆长是否有关
【结论】单摆振动周期和摆长有关
荷兰物理学家惠更斯通过实验进一步找到:
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
1.利用单摆的等时性计时
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)。
2. 用单摆测定重力加速度
周期T=2s的单摆叫做秒摆(摆长约为1米)
四. 单摆的应用
【例】一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s。
(1)求当地的重力加速度g的大小。
(2)把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2,则该单摆振动周期是多少
解析: (1)周期T= s=2.84 s
由周期公式T=2π得
g= m/s2=9.78 m/s2。
(2)T'=2π=2×3.14× s=7.02 s。
【练习】(多选)如下图所示为同一地点的两单摆甲、乙的振动图象,下列说法中正确的是( ABD )
A.甲、乙两单摆的摆长相等
B.甲摆的振幅比乙摆大
C.甲摆的机械能比乙摆大
D.在t= 0.5 s时有正向最大加速度的是乙摆
课堂小结
第二章 机械振动
第4节 单摆
温故知新
1、什么是简谐运动
2、做简谐运动物体的回复力有什么特点
知识回顾
① x-t 图像为正弦曲线
② F-x 满足 F=-kx 的形式
满足 F=-kx的形式且总是指向平衡位置
生活中经常可以看到悬挂起来的物体在竖直平面内往复运动。
摆动的钟摆、荡起的秋千、晃动的枝条它们在平衡位置附近的往复运动是不是简谐运动呢?为了解决这个问题,让我们认识一个新的模型 —— 单摆。
一. 单摆
1. 定义 : 细线一端固定在悬点,另一端系一个小球,如果细线的长度不可改变,细线的质量与小球相比可以忽略,球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
(理想化模型)
2. 模型条件 :
(1)摆球:可看成质点(体积小 质量大)
(2)摆线:① 质量远小于摆球质量
② 长度远大于小球直径
③ 不可伸缩,伸长量忽略不计。
(3)空气阻力远小于摆球的重力
注意:实际应用的单摆小球大小不可忽略,
摆长 L=摆线长度+小球半径
摆长: 摆球重心到摆动圆弧圆心的距离。
偏角: 摆到最高点时,细线与竖直方向的夹角。
3. 单摆的结构:
【思考与讨论】用什么方法探究单摆的振动是否为简谐运动?
1. 位移与时间的关系是否满足正弦关系(x–t 图像法)
2. 回复力与位移是否成正比且方向相反(F=-kx)
回复力来源: F G1 mgsin
角很小时(θ<5°),用弧度制表示的与它的正弦值近似相等 sin
即:F = G1 mgsin mg x (方向与位移方向相反),满足 F k x 形式。
结论:在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动。
一般偏角 F k x (k )
二. 单摆的回复力
三. 单摆的周期
单摆振动的周期与哪些因素有关呢?
1、猜想:
2、证明方法:
控制变量法
【实验1】周期与摆球的质量是否有关
【结论】单摆振动周期和摆球质量无关
【实验2】周期是否与振幅有关?
【结论】单摆的振动周期与其振幅无关(等时性)
【实验3】周期与摆球的摆长是否有关
【结论】单摆振动周期和摆长有关
荷兰物理学家惠更斯通过实验进一步找到:
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
1.利用单摆的等时性计时
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)。
2. 用单摆测定重力加速度
周期T=2s的单摆叫做秒摆(摆长约为1米)
四. 单摆的应用
【例】一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s。
(1)求当地的重力加速度g的大小。
(2)把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2,则该单摆振动周期是多少
解析: (1)周期T= s=2.84 s
由周期公式T=2π得
g= m/s2=9.78 m/s2。
(2)T'=2π=2×3.14× s=7.02 s。
【练习】(多选)如下图所示为同一地点的两单摆甲、乙的振动图象,下列说法中正确的是( ABD )
A.甲、乙两单摆的摆长相等
B.甲摆的振幅比乙摆大
C.甲摆的机械能比乙摆大
D.在t= 0.5 s时有正向最大加速度的是乙摆
课堂小结
