1.4 解直角三角形分层练习(含答案)
文档属性
| 名称 | 1.4 解直角三角形分层练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 879.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 21:14:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,△AOB中,∠ABO=90°,点B在x轴上,点A坐标为(2,2),将△AOB绕点O逆时针旋转15°,此时点A的对应点A′的坐标是( )
A.(,) B.(,)
C.(,) D.(1,)
2.如图,已知点A是第一象限内横坐标为2的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长为( ).
A. B. C.4 D.
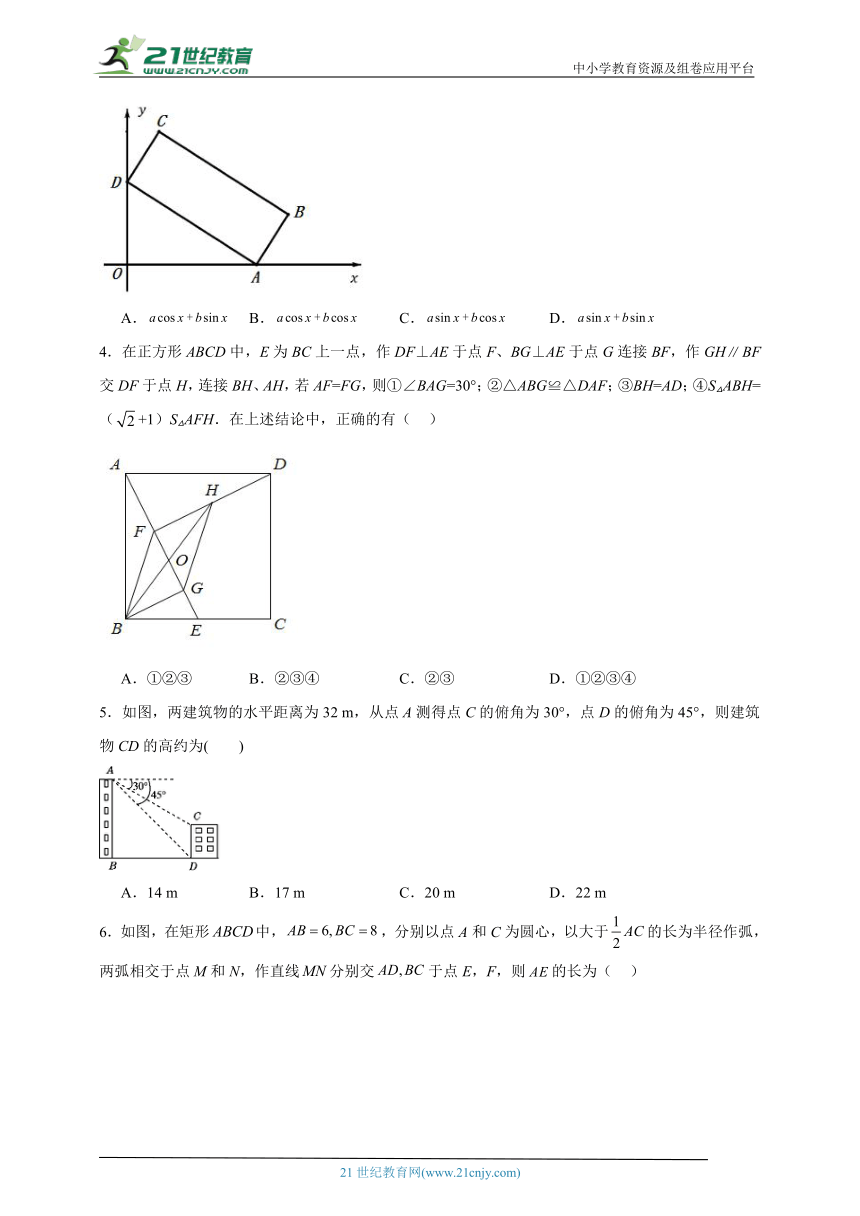
3.如图,在平面直角坐标系中,矩形的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边.则点C到x轴的距离等于( )
A. B. C. D.
4.在正方形ABCD中,E为BC上一点,作DF⊥AE于点F、BG⊥AE于点G连接BF,作GHBF交DF于点H,连接BH、AH,若AF=FG,则①∠BAG=30°;②△ABG≌△DAF;③BH=AD;④S△ABH=(+1)S△AFH.在上述结论中,正确的有( )
A.①②③ B.②③④ C.②③ D.①②③④
5.如图,两建筑物的水平距离为32 m,从点A测得点C的俯角为30°,点D的俯角为45°,则建筑物CD的高约为( )
A.14 m B.17 m C.20 m D.22 m
6.如图,在矩形中,,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线分别交于点E,F,则的长为( )
A. B. C. D.
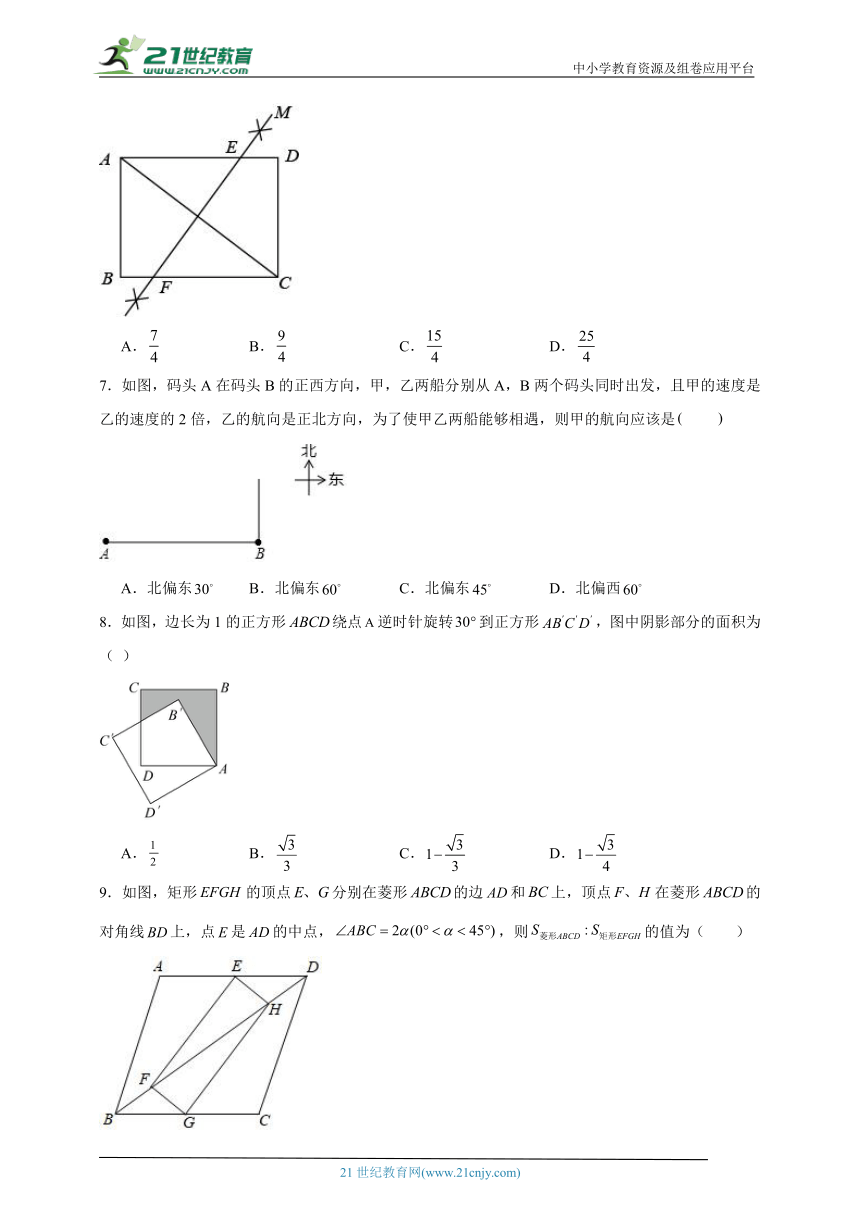
7.如图,码头A在码头B的正西方向,甲,乙两船分别从A,B两个码头同时出发,且甲的速度是乙的速度的2倍,乙的航向是正北方向,为了使甲乙两船能够相遇,则甲的航向应该是
A.北偏东 B.北偏东 C.北偏东 D.北偏西
8.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为( )
A. B. C. D.
9.如图,矩形的顶点分别在菱形的边和上,顶点在菱形的对角线上,点是的中点,,则的值为( )
A.4 B. C. D.
10.如图,在菱形中,对角线相交于点O,,,则线段的长为( )
A.5 B. C.10 D.
二、填空题
11.如图,在平行四边形中,,,,是上的一点,且,则的长为
12.如图,在平面直角坐标系中,点,绕坐标原点将顺时针旋转,得.当点的对应点落在的延长线上时,点的对应点的坐标是 .
13.已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为(即cosC=),则AC边上的中线长是 .
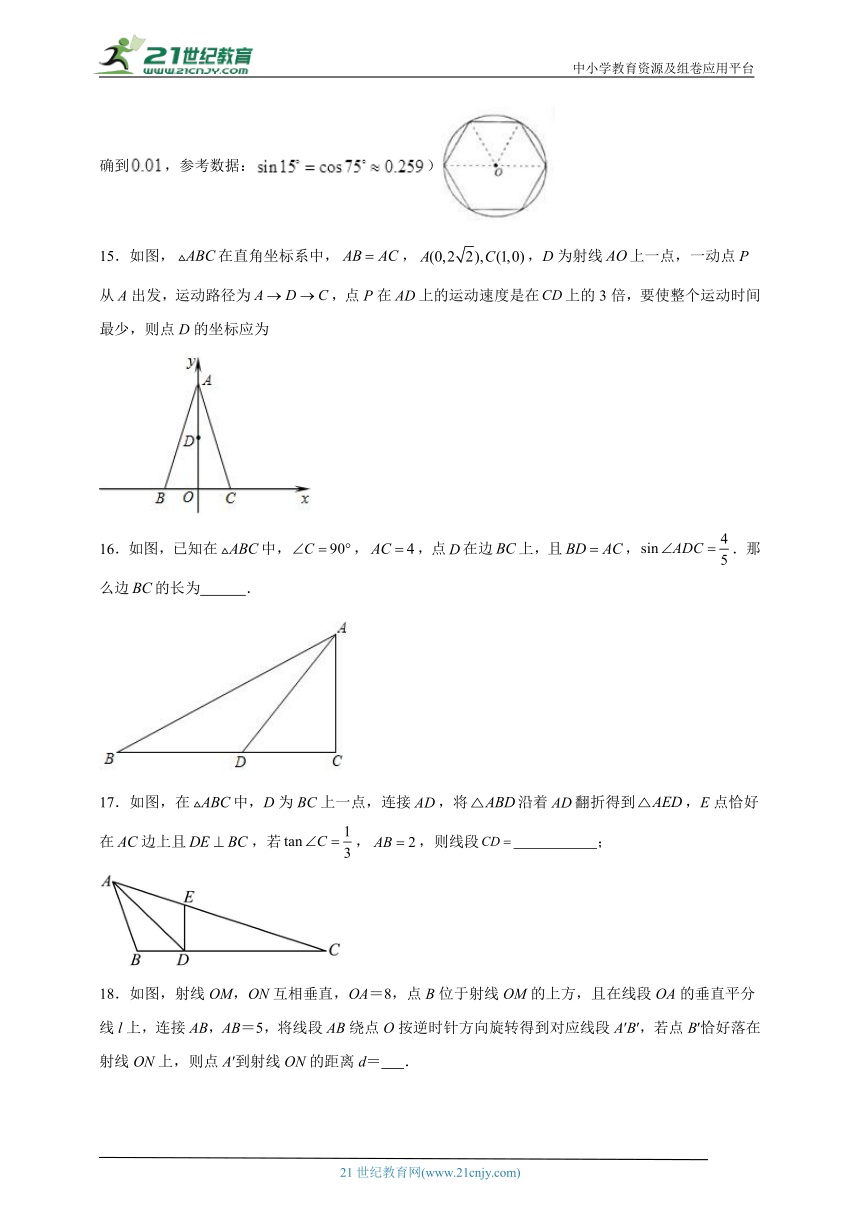
14.我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率的近似值.设半径为的圆内接正边形的周长为,圆的直径为.如右图所示,当时,,那么当时, .(结果精确到,参考数据:)
15.如图,在直角坐标系中,,,D为射线上一点,一动点P从A出发,运动路径为,点P在上的运动速度是在上的3倍,要使整个运动时间最少,则点D的坐标应为
16.如图,已知在中,,,点在边上,且,.那么边的长为 .
17.如图,在中,D为BC上一点,连接,将沿着翻折得到,E点恰好在边上且,若,,则线段 ;
18.如图,射线OM,ON互相垂直,OA=8,点B位于射线OM的上方,且在线段OA的垂直平分线l上,连接AB,AB=5,将线段AB绕点O按逆时针方向旋转得到对应线段A′B′,若点B′恰好落在射线ON上,则点A′到射线ON的距离d= .
19.如图,现有一矩形纸片,为矩形的对角线,,,点为上一点,沿线段将折叠为,交于点,连接,作点关于线段对称的点,点恰好落在对角线上,连接,.则的大小为 ;的长为 .
20.如图,已知边长为2的等边三角形ABC中,分别以点A,C为圆心,m为半径作弧,两弧交于点D,连结BD.若BD的长为2,则m的值为 .
三、解答题
21.体育场主席台侧面如图,若顶棚顶端与看台底端连线和地面垂直,测得看台的长为米,.
(1)求看台高的长;
(2)求顶棚顶端到地面的距离的长. (取)
22.如图1,在中,,点是延长线上的一点,,垂足为,联结.
(1)求证:
(2)当点是中点时,求的值;
(3)如图2,的延长线交的平行线于点,求证:
23.已知平行四边形ABCD中,对角线AC和BD相交于点O,AC=10,
BD=8.
(1)若AC⊥BD,试求四边形ABCD的面积 ;
(2)若AC与BD的夹角∠AOD=,求四边形ABCD的面积;
(3)试讨论:若把题目中“平行四边形ABCD”改为“四边形ABCD”,且∠AOD=
AC=,BD=,试求四边形ABCD的面积(用含,,的代数式表示).
24.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点P从点A出发沿线段AB以每秒3个单位长度的速度运动至点B,过点P作PQ⊥AB交射线AC于点Q.设点P的运动时间为t秒(t>0).
(1)线段AQ的长为 ,线段PQ的长为 .(用含t的代数式表示);
(2)当△APQ与△ABC的周长比为1:4时,求t的值;
(3)设△APQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
25.如图,在中,,,为中点,点在延长线上,,,,交于点.
(1)若,求的度数;
(2)求证:;
(3)设交于点.
①若,,求的值;
②连结,分别记,,的面积为,,,当时, .(直接写出答案)
参考答案:
1.A
2.B
3.A
4.C
5.A
6.D
7.B
8.C
9.C
10.A
11.2
12.
13.或
14.3.10.
15.(0,).
16.7
17.
18.
19. 75
20.2或2.
21.(1)米 ;(2)米.
22.(1)略;(2);(3)略.
23.(1)40
(2)
(3)ab
24.(1),
(2)为秒
(3);
(4)的值为秒或2秒
25.(1)略;(2)略;(3)①;②.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,△AOB中,∠ABO=90°,点B在x轴上,点A坐标为(2,2),将△AOB绕点O逆时针旋转15°,此时点A的对应点A′的坐标是( )
A.(,) B.(,)
C.(,) D.(1,)
2.如图,已知点A是第一象限内横坐标为2的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长为( ).
A. B. C.4 D.
3.如图,在平面直角坐标系中,矩形的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边.则点C到x轴的距离等于( )
A. B. C. D.
4.在正方形ABCD中,E为BC上一点,作DF⊥AE于点F、BG⊥AE于点G连接BF,作GHBF交DF于点H,连接BH、AH,若AF=FG,则①∠BAG=30°;②△ABG≌△DAF;③BH=AD;④S△ABH=(+1)S△AFH.在上述结论中,正确的有( )
A.①②③ B.②③④ C.②③ D.①②③④
5.如图,两建筑物的水平距离为32 m,从点A测得点C的俯角为30°,点D的俯角为45°,则建筑物CD的高约为( )
A.14 m B.17 m C.20 m D.22 m
6.如图,在矩形中,,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线分别交于点E,F,则的长为( )
A. B. C. D.
7.如图,码头A在码头B的正西方向,甲,乙两船分别从A,B两个码头同时出发,且甲的速度是乙的速度的2倍,乙的航向是正北方向,为了使甲乙两船能够相遇,则甲的航向应该是
A.北偏东 B.北偏东 C.北偏东 D.北偏西
8.如图,边长为1的正方形绕点逆时针旋转到正方形,图中阴影部分的面积为( )
A. B. C. D.
9.如图,矩形的顶点分别在菱形的边和上,顶点在菱形的对角线上,点是的中点,,则的值为( )
A.4 B. C. D.
10.如图,在菱形中,对角线相交于点O,,,则线段的长为( )
A.5 B. C.10 D.
二、填空题
11.如图,在平行四边形中,,,,是上的一点,且,则的长为
12.如图,在平面直角坐标系中,点,绕坐标原点将顺时针旋转,得.当点的对应点落在的延长线上时,点的对应点的坐标是 .
13.已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为(即cosC=),则AC边上的中线长是 .
14.我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率的近似值.设半径为的圆内接正边形的周长为,圆的直径为.如右图所示,当时,,那么当时, .(结果精确到,参考数据:)
15.如图,在直角坐标系中,,,D为射线上一点,一动点P从A出发,运动路径为,点P在上的运动速度是在上的3倍,要使整个运动时间最少,则点D的坐标应为
16.如图,已知在中,,,点在边上,且,.那么边的长为 .
17.如图,在中,D为BC上一点,连接,将沿着翻折得到,E点恰好在边上且,若,,则线段 ;
18.如图,射线OM,ON互相垂直,OA=8,点B位于射线OM的上方,且在线段OA的垂直平分线l上,连接AB,AB=5,将线段AB绕点O按逆时针方向旋转得到对应线段A′B′,若点B′恰好落在射线ON上,则点A′到射线ON的距离d= .
19.如图,现有一矩形纸片,为矩形的对角线,,,点为上一点,沿线段将折叠为,交于点,连接,作点关于线段对称的点,点恰好落在对角线上,连接,.则的大小为 ;的长为 .
20.如图,已知边长为2的等边三角形ABC中,分别以点A,C为圆心,m为半径作弧,两弧交于点D,连结BD.若BD的长为2,则m的值为 .
三、解答题
21.体育场主席台侧面如图,若顶棚顶端与看台底端连线和地面垂直,测得看台的长为米,.
(1)求看台高的长;
(2)求顶棚顶端到地面的距离的长. (取)
22.如图1,在中,,点是延长线上的一点,,垂足为,联结.
(1)求证:
(2)当点是中点时,求的值;
(3)如图2,的延长线交的平行线于点,求证:
23.已知平行四边形ABCD中,对角线AC和BD相交于点O,AC=10,
BD=8.
(1)若AC⊥BD,试求四边形ABCD的面积 ;
(2)若AC与BD的夹角∠AOD=,求四边形ABCD的面积;
(3)试讨论:若把题目中“平行四边形ABCD”改为“四边形ABCD”,且∠AOD=
AC=,BD=,试求四边形ABCD的面积(用含,,的代数式表示).
24.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点P从点A出发沿线段AB以每秒3个单位长度的速度运动至点B,过点P作PQ⊥AB交射线AC于点Q.设点P的运动时间为t秒(t>0).
(1)线段AQ的长为 ,线段PQ的长为 .(用含t的代数式表示);
(2)当△APQ与△ABC的周长比为1:4时,求t的值;
(3)设△APQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
25.如图,在中,,,为中点,点在延长线上,,,,交于点.
(1)若,求的度数;
(2)求证:;
(3)设交于点.
①若,,求的值;
②连结,分别记,,的面积为,,,当时, .(直接写出答案)
参考答案:
1.A
2.B
3.A
4.C
5.A
6.D
7.B
8.C
9.C
10.A
11.2
12.
13.或
14.3.10.
15.(0,).
16.7
17.
18.
19. 75
20.2或2.
21.(1)米 ;(2)米.
22.(1)略;(2);(3)略.
23.(1)40
(2)
(3)ab
24.(1),
(2)为秒
(3);
(4)的值为秒或2秒
25.(1)略;(2)略;(3)①;②.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
