1.6 利用三角函数测高分层练习(含答案)
文档属性
| 名称 | 1.6 利用三角函数测高分层练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 548.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-20 21:16:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
1.6利用三角函数测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
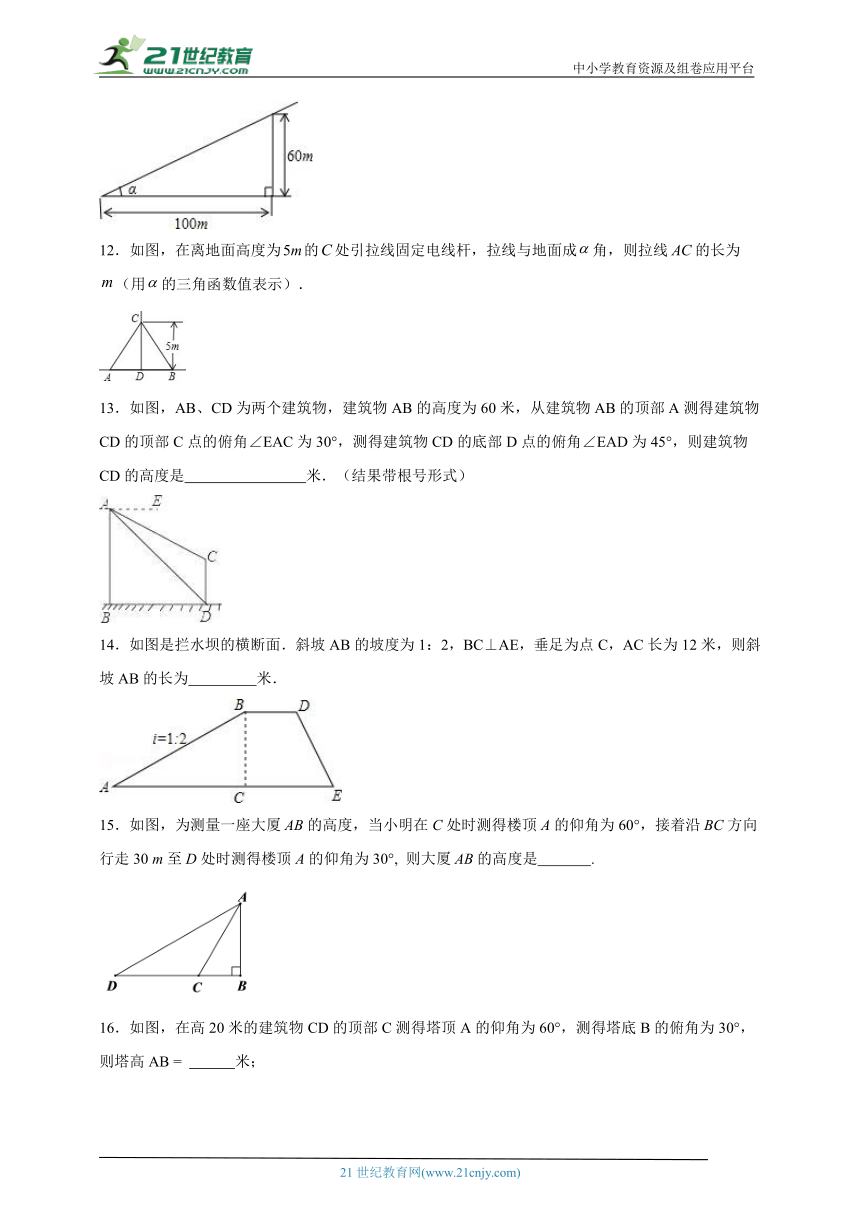
1.如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B离水平面的高度BC的长为 ( )
A.40米 B.米 C.米 D.10米
2.如图①为折叠椅,图②是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长度相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32 cm,∠DOB=100°,那么椅腿AB的长应设计为(结果精确到0.1 cm,参考数据:sin50°=cos40°≈0.77,sin40°=cos50°≈0.64,tan40°≈0.84,tan50°≈1.19)( )
A.38.1 cm B.49.8 cm C.41.6 cm D.45.3 cm
3.如图,河坝横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
A.9m B.6m C. D.
4.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
A.250 B.500 C.250 D.500
5.如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )
A.m B.m C.m D.m
6.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20 m,高度DC=30 m,则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35+55)m B.(25+45)m C.(25+75)m D.(50+20)m
7.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40海里 B.40海里 C.80海里 D.40海里
8.某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠BAP=( )
A. B. C. D.
9.如图,已知点、点是同一幢楼上的两个不同位置,从点观测标志物的俯角是65°,从点观测标志物的俯角是35°,则的度数为( )
A.25° B.30° C.35° D.65°
10.如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,,BC的长是10m,则乘电梯从点B到点C上升的高度是 ( )
A. B.5 C. D.10
二、填空题
11.如图,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度i(即tanα)就是 .
12.如图,在离地面高度为的处引拉线固定电线杆,拉线与地面成角,则拉线的长为 (用的三角函数值表示).
13.如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,则建筑物CD的高度是 米.(结果带根号形式)
14.如图是拦水坝的横断面.斜坡AB的坡度为1:2,BC⊥AE,垂足为点C,AC长为12米,则斜坡AB的长为 米.
15.如图,为测量一座大厦AB的高度,当小明在C处时测得楼顶A的仰角为60°,接着沿BC方向行走30 m至D处时测得楼顶A的仰角为30°, 则大厦AB的高度是 .
16.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
17.如图,小阳发现电线杆的影子落在土坡的坡面和地面上,量得,米,与地面成角,且此时测得米的影长为米,则电线杆的高度为 米.
18.如图,ΔABC中,AB=2.5cm,BC=4cm, 则ΔABC的高AD与CE的比是 .
19.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为100m,那么该建筑物的高度BC约为 m.
20.在Rt△ABC中,∠B=90°,AC=15,sinC=,则AB= .
三、解答题
21.如图,两座建筑物的水平距离为30m,从点测得点的俯角为35°,测得点的俯角为43°,求这两座建筑物的高度(结果保留小数点后1 位,参考数据,,,,,).
22.如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A,某人在岸边的B处测得A在B的北偏东60°的方向上,然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据:≈1.732)
23.在某市地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示).已知立杆的高度是米,从路侧点处测得路况警示牌顶端点和底端点的仰角分别是和,求路况警示牌宽的值.(精确到0.1米)(参考数据:≈1.41,≈1.73)
24.如图,一艘核潜艇在海面下500米的A点处测得俯角为正前方的海底有黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度.(保留根号)
25.如图所示,某学校教学活动小组欲测量一颗大树AB的高度,他们在斜坡上C处测得大树顶端B的仰角是30°,朝大树方向沿斜坡向下走6m到达坡脚D处,在D处测得大树顶端B的仰角是45°,若斜坡CD的坡比i=1:,求大树的高度AB.(结果精确到0.1m,参考数据:,)
参考答案:
1.A
2.C
3.B
4.C
5.D
6.C
7.A
8.A
9.B
10.B
11.0.6
12.
13.60-20.
14.6.
15.15
16.80
17.(14+2)米
18.5:8
19.
20.9.
21.AB≈27.9m;CD≈6.9m
22.这个铜像底部A到岸边BC的距离是173.2米.
23.2.2米
24.海底黑匣子C点处距离海面的深度为()米
25.大树AB的高度约为14.2m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.6利用三角函数测高
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B离水平面的高度BC的长为 ( )
A.40米 B.米 C.米 D.10米
2.如图①为折叠椅,图②是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长度相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32 cm,∠DOB=100°,那么椅腿AB的长应设计为(结果精确到0.1 cm,参考数据:sin50°=cos40°≈0.77,sin40°=cos50°≈0.64,tan40°≈0.84,tan50°≈1.19)( )
A.38.1 cm B.49.8 cm C.41.6 cm D.45.3 cm
3.如图,河坝横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
A.9m B.6m C. D.
4.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.
A.250 B.500 C.250 D.500
5.如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )
A.m B.m C.m D.m
6.如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20 m,高度DC=30 m,则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35+55)m B.(25+45)m C.(25+75)m D.(50+20)m
7.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40海里 B.40海里 C.80海里 D.40海里
8.某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,那么tan∠BAP=( )
A. B. C. D.
9.如图,已知点、点是同一幢楼上的两个不同位置,从点观测标志物的俯角是65°,从点观测标志物的俯角是35°,则的度数为( )
A.25° B.30° C.35° D.65°
10.如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,,BC的长是10m,则乘电梯从点B到点C上升的高度是 ( )
A. B.5 C. D.10
二、填空题
11.如图,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度i(即tanα)就是 .
12.如图,在离地面高度为的处引拉线固定电线杆,拉线与地面成角,则拉线的长为 (用的三角函数值表示).
13.如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,则建筑物CD的高度是 米.(结果带根号形式)
14.如图是拦水坝的横断面.斜坡AB的坡度为1:2,BC⊥AE,垂足为点C,AC长为12米,则斜坡AB的长为 米.
15.如图,为测量一座大厦AB的高度,当小明在C处时测得楼顶A的仰角为60°,接着沿BC方向行走30 m至D处时测得楼顶A的仰角为30°, 则大厦AB的高度是 .
16.如图,在高20米的建筑物CD的顶部C测得塔顶A的仰角为60°,测得塔底B的俯角为30°,则塔高AB = 米;
17.如图,小阳发现电线杆的影子落在土坡的坡面和地面上,量得,米,与地面成角,且此时测得米的影长为米,则电线杆的高度为 米.
18.如图,ΔABC中,AB=2.5cm,BC=4cm, 则ΔABC的高AD与CE的比是 .
19.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为100m,那么该建筑物的高度BC约为 m.
20.在Rt△ABC中,∠B=90°,AC=15,sinC=,则AB= .
三、解答题
21.如图,两座建筑物的水平距离为30m,从点测得点的俯角为35°,测得点的俯角为43°,求这两座建筑物的高度(结果保留小数点后1 位,参考数据,,,,,).
22.如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A,某人在岸边的B处测得A在B的北偏东60°的方向上,然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据:≈1.732)
23.在某市地铁施工期间,交管部门在施工路段设立了矩形路况警示牌(如图所示).已知立杆的高度是米,从路侧点处测得路况警示牌顶端点和底端点的仰角分别是和,求路况警示牌宽的值.(精确到0.1米)(参考数据:≈1.41,≈1.73)
24.如图,一艘核潜艇在海面下500米的A点处测得俯角为正前方的海底有黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度.(保留根号)
25.如图所示,某学校教学活动小组欲测量一颗大树AB的高度,他们在斜坡上C处测得大树顶端B的仰角是30°,朝大树方向沿斜坡向下走6m到达坡脚D处,在D处测得大树顶端B的仰角是45°,若斜坡CD的坡比i=1:,求大树的高度AB.(结果精确到0.1m,参考数据:,)
参考答案:
1.A
2.C
3.B
4.C
5.D
6.C
7.A
8.A
9.B
10.B
11.0.6
12.
13.60-20.
14.6.
15.15
16.80
17.(14+2)米
18.5:8
19.
20.9.
21.AB≈27.9m;CD≈6.9m
22.这个铜像底部A到岸边BC的距离是173.2米.
23.2.2米
24.海底黑匣子C点处距离海面的深度为()米
25.大树AB的高度约为14.2m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
