2.2 位移变化规律 课件 (共40张PPT) 高一物理鲁科版必修第一册
文档属性
| 名称 | 2.2 位移变化规律 课件 (共40张PPT) 高一物理鲁科版必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-20 00:00:00 | ||
图片预览




文档简介
(共40张PPT)
第2章 匀变速直线运动
第2节 位移变化规律
1.匀变速直线运动的位移一时间关系
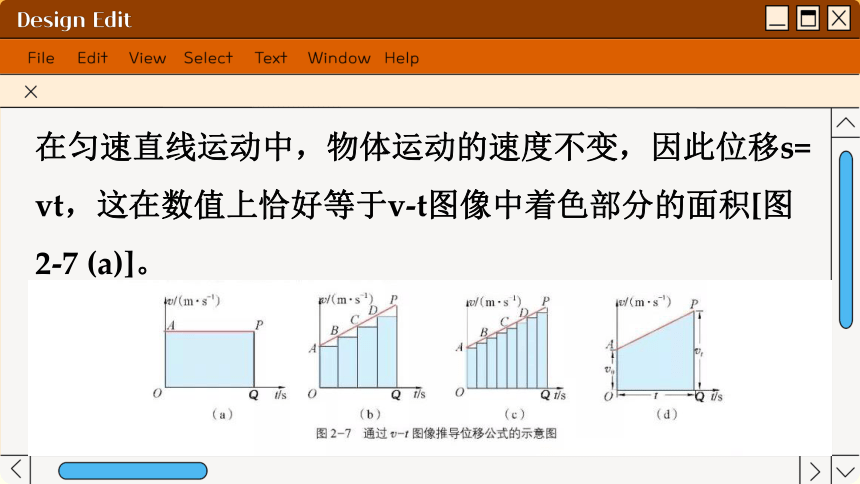
在匀速直线运动中,物体运动的速度不变,因此位移s= vt,这在数值上恰好等于v-t图像中着色部分的面积[图 2-7 (a)]。
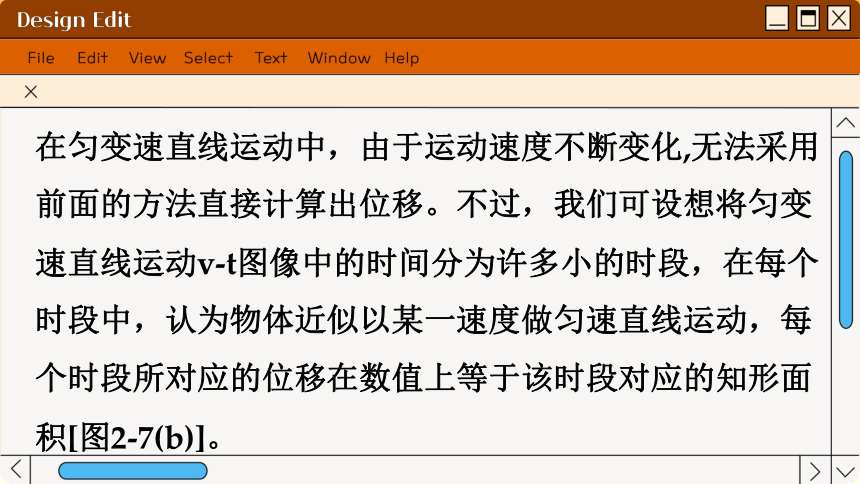
在匀变速直线运动中,由于运动速度不断变化,无法采用前面的方法直接计算出位移。不过,我们可设想将匀变速直线运动v-t图像中的时间分为许多小的时段,在每个时段中,认为物体近似以某一速度做匀速直线运动,每个时段所对应的位移在数值上等于该时段对应的知形面积[图2-7(b)]。
时段划分越细,设想的运动就越接近真实运动,知形面积之和就越接近梯形OAPQ的面积[图 2-7(c)]。当所取的时段足够小时,设想的运动使可等同于真实运动,矩形面积之和便等于梯形面积[图2-7(d)]。
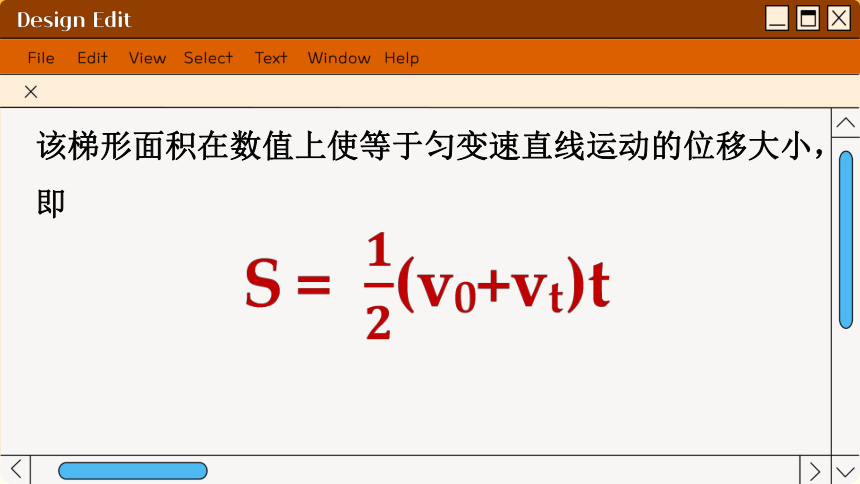
该梯形面积在数值上使等于匀变速直线运动的位移大小,即
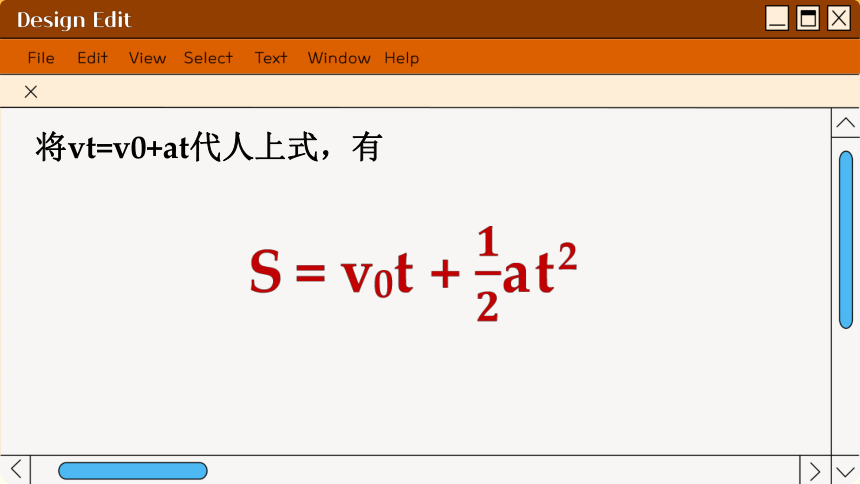
将vt=v0+at代人上式,有
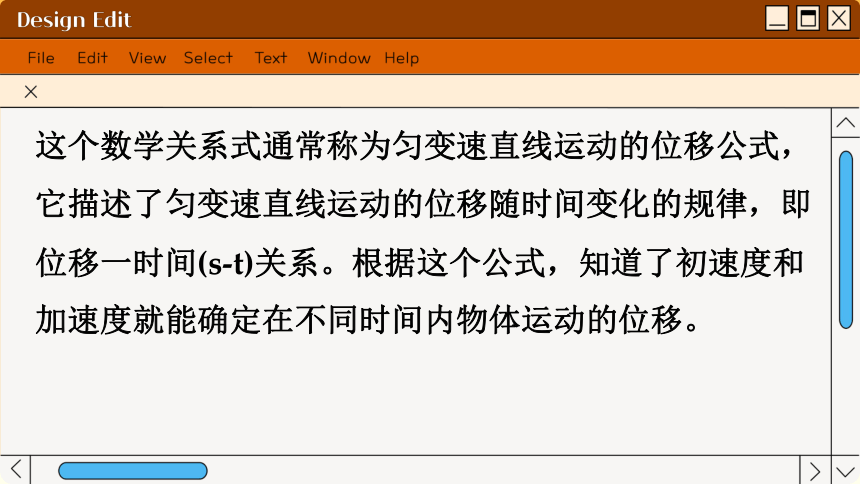
这个数学关系式通常称为匀变速直线运动的位移公式,它描述了匀变速直线运动的位移随时间变化的规律,即位移一时间(s-t)关系。根据这个公式,知道了初速度和加速度就能确定在不同时间内物体运动的位移。
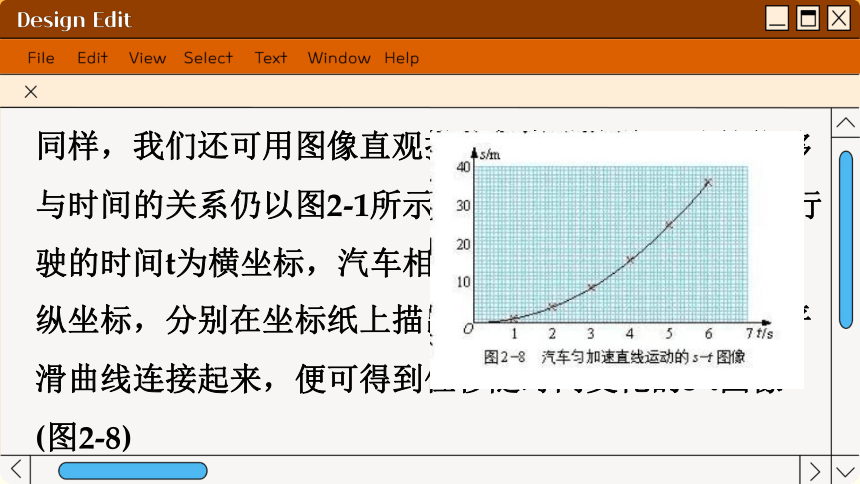
同样,我们还可用图像直观描述匀变速直线运动的位移与时间的关系仍以图2-1所示的汽车运动为例。选汽车行驶的时间t为横坐标,汽车相对于其起始位置的位移s为纵坐标,分别在坐标纸上描出相应的点,再将各点用平滑曲线连接起来,便可得到位移随时间变化的s-t图像(图2-8)
从s-t图像中我们可直观看出物体运动过程中位移随时间的变化情况,并可求出不同时间内物体运动的位移。
2.匀变速直线运动的位移一速度关系
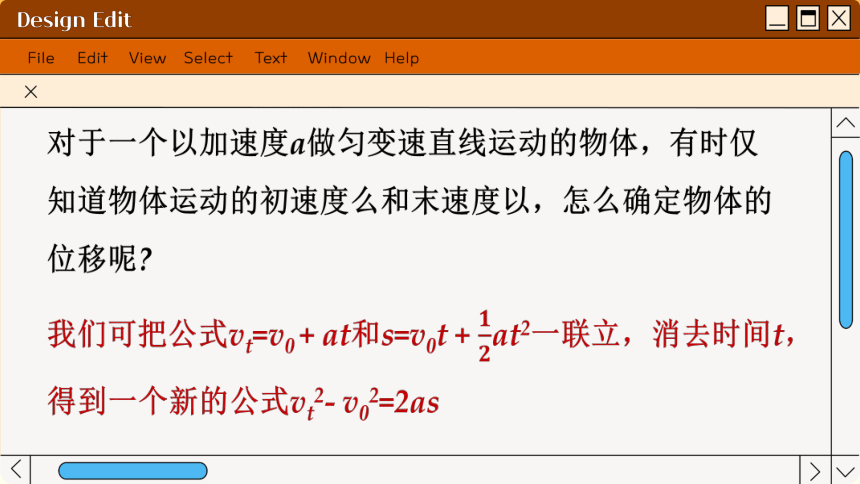
对于一个以加速度a做匀变速直线运动的物体,有时仅知道物体运动的初速度么和末速度以,怎么确定物体的位移呢
我们可把公式vt=v0 + at和s=v0t + at2一联立,消去时间t,得到一个新的公式vt2- v02=2as
这便是匀变速直线运动的位移一速度(s-v)关系式。根据这个公式,在没有时间信息时,我们也可用位移与速度的关系分析物体运动的相关情况。
例题
汽车从开始制动到停止所行驶的距离,是衡量汽车制动性能的参数之一。某型号的汽车以100km/h的速度在柏油路面上行驶急刹车后做减速直线运动。若减速时的加速度大小为5m/s2开始制动后2s内车行驶的高是多少 从开始制动到完全停止汽车行驶的距离是多少
分析
汽车刹车后做匀减速直线运动,运动过程如图2-9所示。在第一问中,已知初速度加速度和时间的信息求位移,可用位移一时间关系式,在第二问中,通过初速度、加速度和末速度的信息求位移,可用位移—速度关系式。
解:选定初速度方向为正方向,由题意知
v0=100km/h=27.8 m/s, a=-5m/s2,vt=0,t=2s。
根据速度公式vt=v0+at,可知汽车刹车时间
t0==5.56s
因为tS1=v0t+at
= 27.8m/s×2s+×(-5m/s2)×(2s)2
= 45.6 m
根据公式=2as,可得汽车从开始制动到完全停止的位移
s2=
=77.3 m
所以,开始制动后2s内汽车行驶的距离为45.6m;从开始制动到完全停止,汽车行驶的距离为77.3m。
讨论
一般以速度 100 km/h 行驶的汽车,从开始制动到完全停止的距离为几十米。本题的计算结果在合理范围内。由于汽车从刹车到停止仍需行驶一段距离,同向行驶的汽车之间需保持一定的安全距离。
你认为以 100 km/h行驶的汽车需与前车保持多大的安全距离 把你的看法与查阅的相关数据进行比较。此外,在其他条件不变的情况下,汽车从开始制动到完全停止所行驶的距离与刹车时速度的平方成正比。你能证明吗 当汽车行驶速度增大时,该距离将显著增大。因此,汽车超速行驶极易引发交通事故。
迁移
我国道路交通安全法规定,机动车因故障在高速公路临时停车时,需在故障车来车方向150m以外设置警告标志。某司机驾驶汽车以120 km/h的速度在高速公路上匀速行驶,发现前方警告标志时刹车使汽车减速至停止。
该司机从发现警告标志到汽车开始制动的反应时间为0.6s制动时的加速度大小为5m/s2 。假设制动后,汽车做减速直线运动,那么从司机发现警告标志到汽车停下,行驶的距高是多少 请解释上述交通法规的必要性。
11.解析 以汽车运动的方向为正方向,则汽车匀速行驶的速度 v0=120 km/h=100m/s ,
在司机从发现警告标志到汽车开始制动的反应时间At=0.6s内汽车做匀速直线运动,行驶的位移
x1=v0Δt=20 m。
节练习
1.一辆电动车以4 m/s 的速度沿直线匀速行驶,然后以1 m/s2的加速度匀速行驶。求电动车匀加速行驶10m时的速度。
解:设初速度4m/s为V0,加速度2m/s2为a,速度10m/s为V1,经历时间为t,经历2秒后的速度为V2
因为物体做匀加速运动,
2.若某汽车以18 m/s 的速度行驶,刹车后做匀减速直线运动,加速度大小为4 m/s2,求到车后5s内汽车前进的距离。
设汽车速度减为零的时间为to===4.5s,汽车4.5s末速度减为零后停止运动,可知刹车后汽车在5s内前进的距离等于4.5s内汽车前进的距离,则汽车在5s内前进的距离x=t0=40.5m
3.如图所示,在某一段平直的铁路上,一列以144 km/h的速度行驶的动车开始匀减速行驶,经过2min,动车恰好停在车站;在车站停留4min,动车匀加速驶高车站,离开车站2km 时恢复到原来的速度144 km/h。
求:(1)动车减速时的加速度大小;
取动车运动方向为正方向,初速度
V0=144km/h=40m/s
根据匀变速直线运动速度公式v=V0+at
可得a=m/s2=m/s2
(2)动车从开始减速到恢复到原速度这段时间内的平均速度大小。
4.某型号的汽车在以72 km/h的速率行驶时,可以在54 m的距高内停下来;在以36 km/h的速率行驶时,可以在17m的距离内停下来。假设两次刹车中,驾驶员的反应时间和刹车的加速度都相同,求驾驶员的反应时间和刹车时加速度的大小。
取运动方向为正方向,设反应时间为 t,加速度大小为a,v1=72km/h=20m/s,x1=54m,v2 = 36km/h = 10m/s ,x2 =17m ,
则:x1=v1t+
x2=v2t+
由①②得,t=0.7s a=5m/s2
5.试证明:做匀变速直线运动的物休在一段时间内的平均速度等于这段时间中间时刻的瞬时速度。
*6.做匀变速直线运动的物体,设在各个连续相等的时间1内的位移分别是s1,s2,s3,……,sx。如果物体的加速度是a,试证明:
(1)s2-s1=s3-s2=…….=Sx-Sx-1=at2
(2)s4-s1=s5-s2=s6-s3=3at2。
第2章 匀变速直线运动
第2节 位移变化规律
1.匀变速直线运动的位移一时间关系
在匀速直线运动中,物体运动的速度不变,因此位移s= vt,这在数值上恰好等于v-t图像中着色部分的面积[图 2-7 (a)]。
在匀变速直线运动中,由于运动速度不断变化,无法采用前面的方法直接计算出位移。不过,我们可设想将匀变速直线运动v-t图像中的时间分为许多小的时段,在每个时段中,认为物体近似以某一速度做匀速直线运动,每个时段所对应的位移在数值上等于该时段对应的知形面积[图2-7(b)]。
时段划分越细,设想的运动就越接近真实运动,知形面积之和就越接近梯形OAPQ的面积[图 2-7(c)]。当所取的时段足够小时,设想的运动使可等同于真实运动,矩形面积之和便等于梯形面积[图2-7(d)]。
该梯形面积在数值上使等于匀变速直线运动的位移大小,即
将vt=v0+at代人上式,有
这个数学关系式通常称为匀变速直线运动的位移公式,它描述了匀变速直线运动的位移随时间变化的规律,即位移一时间(s-t)关系。根据这个公式,知道了初速度和加速度就能确定在不同时间内物体运动的位移。
同样,我们还可用图像直观描述匀变速直线运动的位移与时间的关系仍以图2-1所示的汽车运动为例。选汽车行驶的时间t为横坐标,汽车相对于其起始位置的位移s为纵坐标,分别在坐标纸上描出相应的点,再将各点用平滑曲线连接起来,便可得到位移随时间变化的s-t图像(图2-8)
从s-t图像中我们可直观看出物体运动过程中位移随时间的变化情况,并可求出不同时间内物体运动的位移。
2.匀变速直线运动的位移一速度关系
对于一个以加速度a做匀变速直线运动的物体,有时仅知道物体运动的初速度么和末速度以,怎么确定物体的位移呢
我们可把公式vt=v0 + at和s=v0t + at2一联立,消去时间t,得到一个新的公式vt2- v02=2as
这便是匀变速直线运动的位移一速度(s-v)关系式。根据这个公式,在没有时间信息时,我们也可用位移与速度的关系分析物体运动的相关情况。
例题
汽车从开始制动到停止所行驶的距离,是衡量汽车制动性能的参数之一。某型号的汽车以100km/h的速度在柏油路面上行驶急刹车后做减速直线运动。若减速时的加速度大小为5m/s2开始制动后2s内车行驶的高是多少 从开始制动到完全停止汽车行驶的距离是多少
分析
汽车刹车后做匀减速直线运动,运动过程如图2-9所示。在第一问中,已知初速度加速度和时间的信息求位移,可用位移一时间关系式,在第二问中,通过初速度、加速度和末速度的信息求位移,可用位移—速度关系式。
解:选定初速度方向为正方向,由题意知
v0=100km/h=27.8 m/s, a=-5m/s2,vt=0,t=2s。
根据速度公式vt=v0+at,可知汽车刹车时间
t0==5.56s
因为t
= 27.8m/s×2s+×(-5m/s2)×(2s)2
= 45.6 m
根据公式=2as,可得汽车从开始制动到完全停止的位移
s2=
=77.3 m
所以,开始制动后2s内汽车行驶的距离为45.6m;从开始制动到完全停止,汽车行驶的距离为77.3m。
讨论
一般以速度 100 km/h 行驶的汽车,从开始制动到完全停止的距离为几十米。本题的计算结果在合理范围内。由于汽车从刹车到停止仍需行驶一段距离,同向行驶的汽车之间需保持一定的安全距离。
你认为以 100 km/h行驶的汽车需与前车保持多大的安全距离 把你的看法与查阅的相关数据进行比较。此外,在其他条件不变的情况下,汽车从开始制动到完全停止所行驶的距离与刹车时速度的平方成正比。你能证明吗 当汽车行驶速度增大时,该距离将显著增大。因此,汽车超速行驶极易引发交通事故。
迁移
我国道路交通安全法规定,机动车因故障在高速公路临时停车时,需在故障车来车方向150m以外设置警告标志。某司机驾驶汽车以120 km/h的速度在高速公路上匀速行驶,发现前方警告标志时刹车使汽车减速至停止。
该司机从发现警告标志到汽车开始制动的反应时间为0.6s制动时的加速度大小为5m/s2 。假设制动后,汽车做减速直线运动,那么从司机发现警告标志到汽车停下,行驶的距高是多少 请解释上述交通法规的必要性。
11.解析 以汽车运动的方向为正方向,则汽车匀速行驶的速度 v0=120 km/h=100m/s ,
在司机从发现警告标志到汽车开始制动的反应时间At=0.6s内汽车做匀速直线运动,行驶的位移
x1=v0Δt=20 m。
节练习
1.一辆电动车以4 m/s 的速度沿直线匀速行驶,然后以1 m/s2的加速度匀速行驶。求电动车匀加速行驶10m时的速度。
解:设初速度4m/s为V0,加速度2m/s2为a,速度10m/s为V1,经历时间为t,经历2秒后的速度为V2
因为物体做匀加速运动,
2.若某汽车以18 m/s 的速度行驶,刹车后做匀减速直线运动,加速度大小为4 m/s2,求到车后5s内汽车前进的距离。
设汽车速度减为零的时间为to===4.5s,汽车4.5s末速度减为零后停止运动,可知刹车后汽车在5s内前进的距离等于4.5s内汽车前进的距离,则汽车在5s内前进的距离x=t0=40.5m
3.如图所示,在某一段平直的铁路上,一列以144 km/h的速度行驶的动车开始匀减速行驶,经过2min,动车恰好停在车站;在车站停留4min,动车匀加速驶高车站,离开车站2km 时恢复到原来的速度144 km/h。
求:(1)动车减速时的加速度大小;
取动车运动方向为正方向,初速度
V0=144km/h=40m/s
根据匀变速直线运动速度公式v=V0+at
可得a=m/s2=m/s2
(2)动车从开始减速到恢复到原速度这段时间内的平均速度大小。
4.某型号的汽车在以72 km/h的速率行驶时,可以在54 m的距高内停下来;在以36 km/h的速率行驶时,可以在17m的距离内停下来。假设两次刹车中,驾驶员的反应时间和刹车的加速度都相同,求驾驶员的反应时间和刹车时加速度的大小。
取运动方向为正方向,设反应时间为 t,加速度大小为a,v1=72km/h=20m/s,x1=54m,v2 = 36km/h = 10m/s ,x2 =17m ,
则:x1=v1t+
x2=v2t+
由①②得,t=0.7s a=5m/s2
5.试证明:做匀变速直线运动的物休在一段时间内的平均速度等于这段时间中间时刻的瞬时速度。
*6.做匀变速直线运动的物体,设在各个连续相等的时间1内的位移分别是s1,s2,s3,……,sx。如果物体的加速度是a,试证明:
(1)s2-s1=s3-s2=…….=Sx-Sx-1=at2
(2)s4-s1=s5-s2=s6-s3=3at2。
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
